Hostname: page-component-848d4c4894-pjpqr Total loading time: 0 Render date: 2024-06-22T05:20:52.521Z Has data issue: false hasContentIssue false
  • English
  • Français

Some Engel conditions on infinite subsets of certain groups

Published online by Cambridge University Press:  17 April 2009

Alireza Abdollahi
Alireza Abdollahi
Affiliation:
Department of Mathematics, University of IsfahanIsfahan 81744, Iran e-mail: abdolahi@math.ui.ac.ir
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let k be a positive integer. We denote by ɛk(∞) the class of all groups in which every infinite subset contains two distinct elements x, y such that [x,k y] = 1. We say that a group G is an 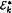-group provided that whenever X, Y are infinite subsets of G, there exists x ∈ X, y ∈ Y such that [x,k y] = 1. Here we prove that:

(1) If G is a finitely generated soluble group, then G ∈ ɛ3(∞) if and only if G is finite by a nilpotent group in which every two generator subgroup is nilpotent of class at most 3.

(2) If G is a finitely generated metabelian group, then G ∈ ɛk(∞) if and only if G/Zk (G) is finite, where Zk (G) is the (k + 1)-th term of the upper central series of G.

(3) If G is a finitely generated soluble ɛk(∞)-group, then there exists a positive integer t depending only on k such that G/Zt (G) is finite.

(4) If G is an infinite 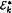-group in which every non-trivial finitely generated subgroup has a non-trivial finite quotient, then G is k-Engel. In particular, G is locally nilpotent.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 62 , Issue 1 , August 2000 , pp. 141 - 148
Copyright
Copyright © Australian Mathematical Society 2000

References

[1]Abdollahi, A., ‘Finitely generated soluble groups with an Engel condition on infinite subsets’, Rend. Sem. Mat. Univ. Padova 103 (2000) (to appear).Google Scholar
[2]Abdollahi, A. and Taeri, B., ‘A condition on finitely generated soluble groups’, Comm. Algebra 27 (1999), 5633–5638.CrossRefGoogle Scholar
[3]Delizia, C., ‘Finitely generated soluble groups with a condition on infinite subsets’, Istit. Lombardo Accad. Sci. Lett. Rend. A 128 (1994), 201–208.Google Scholar
[4]Delizia, C., ‘On certain residually finite groups’, Comm. Algebra 24 (1996), 3531–3535.CrossRefGoogle Scholar
[5]Delizia, C., Rhemtulla, A. and Smith, H., ‘Locally graded groups with a nilpotency condition on infinite subsets’, (to appear).Google Scholar
[6]Endimioni, G., ‘Groups covered by finitely many nilpotent subgroups’, Bull. Austral. Math. Soc. 50 (1994), 459–464.CrossRefGoogle Scholar
[7]Groves, J.R.J., ‘A conjecture of Lennox and Wiegold concerning supersoluble groups’, J. Austral. Math. Soc. Ser. A 35 (1983), 218–228.CrossRefGoogle Scholar
[8]Gruenberg, K.W., ‘The upper central series in soluble groups’, Illinois J. Math. 5 (1961), 436–466.CrossRefGoogle Scholar
[9]Gupta, N.D. and Newman, M.F., ‘On metabelian groups’, J. Austral. Math. Soc. 6 (1966), 362–368.CrossRefGoogle Scholar
[10]Gupta, N.D. and Newman, M.F., ‘Third Engel groups’, Bull. Austral. Math. Soc. 40 (1989), 215–230.CrossRefGoogle Scholar
[11]Hall, P., ‘Finite-by-nilpotent groups’, Proc. Cambridge Philos. Soc. 52 (1956), 611–616.CrossRefGoogle Scholar
[12]Kim, Y.K. and Rhemtulla, A., ‘Weak maximality condition and polycyclic groups’, Proc. Amer. Math. Soc. 123 (1995), 711–714.CrossRefGoogle Scholar
[13]Lennox, J.C. and Wiegold, J., ‘Extensions of a problem of Paul Erdös on groups’, J. Austral. Math. Soc. Ser. A 31 (1981), 459–463.CrossRefGoogle Scholar
[14]Longobardi, P. and Maj, M., ‘Finitely generated soluble groups with an Engel condition on infinite subsets’, Rend. Sem. Mat. Univ. Padova 89 (1993), 97–102.Google Scholar
[15]Longobardi, P., Maj, M. and Rhemtulla, A., ‘Groups with no free subsemigroups’, Trans. Amer. Math. Soc. 347 (1995), 1419–1427.CrossRefGoogle Scholar
[16]Neumann, B.H., ‘A problem of Paul Erdös on groups’, J. Austral. Math. Soc. Ser. A 21 (1976), 467–472.CrossRefGoogle Scholar
[17]Newman, M.F., ‘Some varieties of groups’, J. Austral. Math. Soc. 16 (1973), 481–494.CrossRefGoogle Scholar
[18]Puglisi, O. and Spiezia, L.S., ‘A combinatorial property of certain infinite groups’, Comm. Algebra 22 (1994), 1457–1465.CrossRefGoogle Scholar
[19]Wilson, J.S., ‘Two-generator conditions in residually finite groups’, Bull. London Math. Soc. 23 (1991), 239–248.CrossRefGoogle Scholar
[20]Zel'manov, E.I., ‘On some problems of group theory and algebras’, Math. USSR-Sb. 66 (1990), 159–168.CrossRefGoogle Scholar