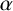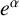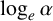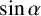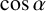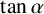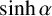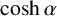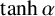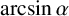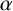1 Introduction
In 1844, Joseph Liouville proved the existence of transcendental numbers [Reference Angell1, Reference Baker2]. He introduced the set
![]() $\mathcal L$
of real numbers, now known as Liouville numbers, and showed that they are all transcendental.
$\mathcal L$
of real numbers, now known as Liouville numbers, and showed that they are all transcendental.
Definition 1.1. A real number
![]() $\xi $
is called a Liouville number if for every positive integer n, there exists a pair of integers
$\xi $
is called a Liouville number if for every positive integer n, there exists a pair of integers
![]() $(p,q)$
with
$(p,q)$
with
![]() $q> 1$
, such that
$q> 1$
, such that
 $$ \begin{align*} 0 < \bigg| \xi - \frac{p}{q} \bigg| < \frac{1}{q^n}. \end{align*} $$
$$ \begin{align*} 0 < \bigg| \xi - \frac{p}{q} \bigg| < \frac{1}{q^n}. \end{align*} $$
Alan Baker in his classic work [Reference Baker2] on transcendental number theory said: ‘A classification of the set of all transcendental numbers into three disjoint aggregates, termed S-, T-, and U-numbers was introduced by Mahler [Reference Mahler8] in 1932, and it has proved to be of considerable value in the general development of the subject’.
In this paper, we demonstrate just how powerful and useful Mahler’s classification of transcendental numbers is.
The following beautiful theorem, which is a corollary of the Lindemann–Weierstrass theorem, appears as Theorem 9.11 in Ivan Niven’s book [Reference Niven12]. We prove the analogous result with ‘algebraic number’ replaced by ‘Liouville number’.
Theorem 1.2. The following numbers are transcendental:
-
(i)
 ${e}^\alpha $
,
${e}^\alpha $
,
 $\sin \alpha $
,
$\sin \alpha $
,
 $\cos \alpha $
,
$\cos \alpha $
,
 $\tan \alpha $
,
$\tan \alpha $
,
 $\sinh \alpha $
,
$\sinh \alpha $
,
 $\cosh \alpha $
,
$\cosh \alpha $
,
 $\tanh \alpha $
;
$\tanh \alpha $
; -
(ii)
 $\log _{e}\alpha , \arcsin \alpha $
and, in general, the inverse functions of all those listed in part (i),
$\log _{e}\alpha , \arcsin \alpha $
and, in general, the inverse functions of all those listed in part (i),
for any nonzero algebraic number
![]() $\alpha $
; wherever multiple values are involved, every such value is transcendental.
$\alpha $
; wherever multiple values are involved, every such value is transcendental.
It is not widely known that
![]() ${e}^\alpha $
and
${e}^\alpha $
and
![]() $\log _{e}\alpha $
are transcendental numbers when
$\log _{e}\alpha $
are transcendental numbers when
![]() $\alpha $
is a Liouville number, though the
$\alpha $
is a Liouville number, though the
![]() $\exp $
case is stated explicitly in [Reference Kumar6, page 98] and the
$\exp $
case is stated explicitly in [Reference Kumar6, page 98] and the
![]() $\log $
case, as pointed out to the second author by Michel Waldschmidt, is implicit in [Reference Bugeaud3, Section 3.5]. The proof in our paper for
$\log $
case, as pointed out to the second author by Michel Waldschmidt, is implicit in [Reference Bugeaud3, Section 3.5]. The proof in our paper for
![]() $\exp $
is different from that in [Reference Kumar6].
$\exp $
is different from that in [Reference Kumar6].
However, the results for the trigonometric and hyperbolic functions do not appear in print. The proofs of all these results for Liouville numbers, and indeed a wider class of numbers, depend on properties of the Mahler classes of transcendental numbers.
Remark 1.3. One might think that the results for trigonometric and hyperbolic functions might follow trivially from the result for
![]() $\exp $
since, for example,
$\exp $
since, for example,
![]() $\cosh (x) =\tfrac 12(\exp (x)+\exp (-x))$
. However, the sum of two transcendental numbers is not necessarily transcendental. Indeed, in 1962, Erdős [Reference Erdős5] proved that every real number is a sum of two Liouville numbers and it is proved in [Reference Chalebgwa and Morris4] that there are
$\cosh (x) =\tfrac 12(\exp (x)+\exp (-x))$
. However, the sum of two transcendental numbers is not necessarily transcendental. Indeed, in 1962, Erdős [Reference Erdős5] proved that every real number is a sum of two Liouville numbers and it is proved in [Reference Chalebgwa and Morris4] that there are
![]() $2^{\mathfrak {c}}$
subsets W of the Liouville numbers such that every real number is the sum of two numbers in W.
$2^{\mathfrak {c}}$
subsets W of the Liouville numbers such that every real number is the sum of two numbers in W.
2 Mahler classes
We follow the presentation in [Reference Bugeaud3, Section 3]. While the definitions and results therein are stated and proved for real numbers, mutatis mutandis, they carry over to the case of complex numbers. Mahler’s classification partitions the set
![]() $\mathbb {C}$
of all complex numbers into four sets (the fourth set in fact turns out to be the set of all algebraic numbers), characterised by the rate with which a nonzero polynomial with integer coefficients approaches zero when evaluated at a particular number.
$\mathbb {C}$
of all complex numbers into four sets (the fourth set in fact turns out to be the set of all algebraic numbers), characterised by the rate with which a nonzero polynomial with integer coefficients approaches zero when evaluated at a particular number.
Given a polynomial
![]() $P(X) \in \mathbb {C}[X]$
, recall that the height of P, denoted by
$P(X) \in \mathbb {C}[X]$
, recall that the height of P, denoted by
![]() $H(P)$
, is the maximum of the absolute values of the coefficients of P. Given a complex number
$H(P)$
, is the maximum of the absolute values of the coefficients of P. Given a complex number
![]() $\xi $
, a positive integer n and a real number
$\xi $
, a positive integer n and a real number
![]() $H \geq 1$
, we define the quantity
$H \geq 1$
, we define the quantity
Furthermore, we set
 $$ \begin{align*} w_n(\xi) = \limsup_{H \rightarrow \infty} \frac{- \log w_n(\xi, H)}{\log H} \end{align*} $$
$$ \begin{align*} w_n(\xi) = \limsup_{H \rightarrow \infty} \frac{- \log w_n(\xi, H)}{\log H} \end{align*} $$
and
With this notation in mind, Mahler partitions the complex numbers into four sets.
Definition 2.1. Let
![]() $\xi $
be a complex number. The number
$\xi $
be a complex number. The number
![]() $\xi $
is:
$\xi $
is:
-
• an A-number if
 $w(\xi ) = 0$
;
$w(\xi ) = 0$
; -
• an S-number if
 $0 < w(\xi ) < \infty $
;
$0 < w(\xi ) < \infty $
; -
• a T-number if
 $w(\xi ) = \infty $
and
$w(\xi ) = \infty $
and
 $w_n(\xi ) < \infty $
for any
$w_n(\xi ) < \infty $
for any
 $n \geq 1$
;
$n \geq 1$
; -
• a U-number if
 $w(\xi ) = \infty $
and
$w(\xi ) = \infty $
and
 $w_n(\xi ) = \infty $
for all
$w_n(\xi ) = \infty $
for all
 $n \geq n_0$
, for some positive integer
$n \geq n_0$
, for some positive integer
 $n_0$
.
$n_0$
.
Remark 2.2. Note that the A-numbers are the algebraic numbers.
The following theorem of Mahler records a fundamental property of the Mahler classes.
Theorem 2.3 (see [Reference Bugeaud3, Theorem 3.2])
If
![]() $\xi , \eta \in \mathbb {C}$
are algebraically dependent, then they belong to the same Mahler class.
$\xi , \eta \in \mathbb {C}$
are algebraically dependent, then they belong to the same Mahler class.
The following theorem of Mahler is key to our main result.
Theorem 2.4 ([Reference Mahler8, Reference Mahler9]; see also [Reference Bugeaud3, Section 3.5])
If a is an algebraic number with
![]() $a\ne 0$
, then
$a\ne 0$
, then
![]() $\exp (a)\in S$
and if
$\exp (a)\in S$
and if
![]() $a\ne 0,1$
, then
$a\ne 0,1$
, then
![]() $\log (a)\in S\cup T$
.
$\log (a)\in S\cup T$
.
Theorem 2.5 [Reference Mahler10]
The number
![]() $\pi \in S\cup T$
.
$\pi \in S\cup T$
.
Remark 2.6. Note that the Liouville numbers are U-numbers. Furthermore, if
![]() $\xi $
is a Liouville number, then
$\xi $
is a Liouville number, then
![]() $i \xi $
is a U-number by Theorem 2.3.
$i \xi $
is a U-number by Theorem 2.3.
3 The main theorem
Theorem 3.1. For any U-number
![]() $\alpha $
, in particular for
$\alpha $
, in particular for
![]() $\alpha $
any Liouville number, all of the following are transcendental numbers:
$\alpha $
any Liouville number, all of the following are transcendental numbers:
![]() ${e}^\alpha $
,
${e}^\alpha $
,
![]() $\log _{e}\alpha $
,
$\log _{e}\alpha $
,
![]() $\sin \alpha $
,
$\sin \alpha $
,
![]() $\cos \alpha $
,
$\cos \alpha $
,
![]() $\tan \alpha $
,
$\tan \alpha $
,
![]() $\sinh \alpha $
,
$\sinh \alpha $
,
![]() $\cosh \alpha $
,
$\cosh \alpha $
,
![]() $\tanh \alpha $
and the inverse functions evaluated at
$\tanh \alpha $
and the inverse functions evaluated at
![]() $\alpha $
of the listed trigonometric and hyperbolic functions, noting that wherever multiple values are involved, every such value is transcendental.
$\alpha $
of the listed trigonometric and hyperbolic functions, noting that wherever multiple values are involved, every such value is transcendental.
Proof. For ease of notation, we adopt the conventional notation that
![]() $\log $
denotes
$\log $
denotes
![]() $\log _{e}$
. We shall demonstrate the result for
$\log _{e}$
. We shall demonstrate the result for
![]() ${e}^\alpha $
,
${e}^\alpha $
,
![]() $\sin \alpha $
,
$\sin \alpha $
,
![]() $\tan \alpha $
,
$\tan \alpha $
,
![]() $\sinh \alpha $
and their inverses. The corresponding proofs for the remaining functions in each family are analogous.
$\sinh \alpha $
and their inverses. The corresponding proofs for the remaining functions in each family are analogous.
Henceforth, let
![]() $\alpha $
be a U-number.
$\alpha $
be a U-number.
(1)
![]() $\exp \alpha $
. Suppose that
$\exp \alpha $
. Suppose that
![]() $\mu = {e}^\alpha $
is an algebraic number. Then,
$\mu = {e}^\alpha $
is an algebraic number. Then,
![]() $\log \mu = \alpha \in S \cup T$
by Theorem 2.4. This is a contradiction since
$\log \mu = \alpha \in S \cup T$
by Theorem 2.4. This is a contradiction since
![]() $\alpha \in U$
. So
$\alpha \in U$
. So
![]() ${e}^\alpha $
is a transcendental number.
${e}^\alpha $
is a transcendental number.
(2)
![]() $\log \alpha $
. Suppose
$\log \alpha $
. Suppose
![]() $\mu $
is one of the values of
$\mu $
is one of the values of
![]() $ \log \alpha $
and is an algebraic number. Then
$ \log \alpha $
and is an algebraic number. Then
![]() ${e}^\mu = \alpha \in S$
by Theorem 2.4. This is a contradiction since
${e}^\mu = \alpha \in S$
by Theorem 2.4. This is a contradiction since
![]() $\alpha \in U$
. So all values of
$\alpha \in U$
. So all values of
![]() $\log \alpha $
are transcendental.
$\log \alpha $
are transcendental.
(3)
![]() $\sin \alpha $
. Suppose
$\sin \alpha $
. Suppose
![]() $\mu = \sin \alpha $
is an algebraic number. Then by Remark 2.6 and Theorem 2.4,
$\mu = \sin \alpha $
is an algebraic number. Then by Remark 2.6 and Theorem 2.4,
![]() $i \alpha \in U$
. By item (1) proved above,
$i \alpha \in U$
. By item (1) proved above,
![]() $t = e^{i \alpha }$
is transcendental. Further,
$t = e^{i \alpha }$
is transcendental. Further,
![]() $2i \sin \alpha = e^{i \alpha } - e^{-i \alpha } = t - {1}/{t} = 2i\mu = \beta $
, where, by our supposition,
$2i \sin \alpha = e^{i \alpha } - e^{-i \alpha } = t - {1}/{t} = 2i\mu = \beta $
, where, by our supposition,
![]() $\beta $
is an algebraic number. Now
$\beta $
is an algebraic number. Now
![]() $t - {1}/{t} = \beta $
implies that
$t - {1}/{t} = \beta $
implies that
![]() $t = \tfrac 12(\,\beta \pm \sqrt {4 - \beta ^2})$
. Since
$t = \tfrac 12(\,\beta \pm \sqrt {4 - \beta ^2})$
. Since
![]() $\beta $
is an algebraic number, the right-hand side of the preceding equation is also an algebraic number, and this is a contradiction since t is a transcendental number. So
$\beta $
is an algebraic number, the right-hand side of the preceding equation is also an algebraic number, and this is a contradiction since t is a transcendental number. So
![]() $\sin \alpha $
is transcendental.
$\sin \alpha $
is transcendental.
(4)
![]() $\arcsin \alpha $
. Suppose first that one of the values of
$\arcsin \alpha $
. Suppose first that one of the values of
![]() $\arcsin \alpha = \mu $
is
$\arcsin \alpha = \mu $
is
![]() $0$
. Then
$0$
. Then
![]() $\alpha =k\pi $
, for some
$\alpha =k\pi $
, for some
![]() $k\in \mathbb {Z}$
. If
$k\in \mathbb {Z}$
. If
![]() $k=0$
, then
$k=0$
, then
![]() $\alpha =0$
which contradicts the fact that
$\alpha =0$
which contradicts the fact that
![]() $\alpha \in U$
. If
$\alpha \in U$
. If
![]() $\alpha =k\pi $
,
$\alpha =k\pi $
,
![]() $k\ne 0$
, then
$k\ne 0$
, then
![]() $k\pi \in S\cup T$
by Theorem 2.5, which contradicts the fact that
$k\pi \in S\cup T$
by Theorem 2.5, which contradicts the fact that
![]() $\alpha \in U$
.
$\alpha \in U$
.
Next suppose that one of the values of
![]() $\arcsin \alpha = \mu $
is an algebraic number. Recall that
$\arcsin \alpha = \mu $
is an algebraic number. Recall that
![]() $\arcsin \alpha = -i \log (i \alpha + \sqrt {1-\alpha ^2})$
. Now,
$\arcsin \alpha = -i \log (i \alpha + \sqrt {1-\alpha ^2})$
. Now,
![]() $i \mu = \log (i \alpha + \sqrt {1-\alpha ^2})$
implies
$i \mu = \log (i \alpha + \sqrt {1-\alpha ^2})$
implies
![]() $e^{i \mu } = \sqrt {1-\alpha ^2} + i \alpha $
. By Theorem 2.4,
$e^{i \mu } = \sqrt {1-\alpha ^2} + i \alpha $
. By Theorem 2.4,
![]() $e^{i \mu } \in S$
. However,
$e^{i \mu } \in S$
. However,
![]() $X = \alpha $
and
$X = \alpha $
and
![]() $Y = \sqrt {1-\alpha ^2} + i \alpha $
satisfy the equation
$Y = \sqrt {1-\alpha ^2} + i \alpha $
satisfy the equation
![]() $P(X,Y) = Y^4 + 4Y^2X^2 - 2Y^2 + 1 = 0$
and hence X and Y are algebraically dependent. So by Theorem 2.3, X and Y are in the same Mahler class. As we are given
$P(X,Y) = Y^4 + 4Y^2X^2 - 2Y^2 + 1 = 0$
and hence X and Y are algebraically dependent. So by Theorem 2.3, X and Y are in the same Mahler class. As we are given
![]() $X\in U$
, this implies
$X\in U$
, this implies
![]() $e^{i\mu }= Y\in U$
which is a contradiction as we saw that
$e^{i\mu }= Y\in U$
which is a contradiction as we saw that
![]() $e^{i\mu }\in S$
. Thus, all values of
$e^{i\mu }\in S$
. Thus, all values of
![]() $\arcsin \alpha $
are transcendental.
$\arcsin \alpha $
are transcendental.
(5)
![]() $\tan \alpha $
. Suppose that
$\tan \alpha $
. Suppose that
![]() $\mu = \tan \alpha $
is algebraic. Then this implies that
$\mu = \tan \alpha $
is algebraic. Then this implies that
![]() $i \mu = {(t - 1/t)}/ {(t + 1/t)}$
is algebraic, where
$i \mu = {(t - 1/t)}/ {(t + 1/t)}$
is algebraic, where
![]() $t = e^{i \alpha }$
, which is transcendental by Theorem 2.4. The former equation implies that
$t = e^{i \alpha }$
, which is transcendental by Theorem 2.4. The former equation implies that
![]() $t^3 + t + i \beta t - i\beta = 0$
, where
$t^3 + t + i \beta t - i\beta = 0$
, where
![]() $\beta = {1}/{\mu }$
. In the interest of brevity, we omit exhibiting the general solution for t, but we note that the polynomial has algebraic coefficients, and hence, each solution t is also algebraic, which is a contradiction.
$\beta = {1}/{\mu }$
. In the interest of brevity, we omit exhibiting the general solution for t, but we note that the polynomial has algebraic coefficients, and hence, each solution t is also algebraic, which is a contradiction.
(6)
![]() $\arctan \alpha $
. Put
$\arctan \alpha $
. Put
![]() $\mu = \arctan \alpha $
, so
$\mu = \arctan \alpha $
, so
![]() $2i \mu = \log ( {(i-\alpha )}/{(i + \alpha )} )$
. As in item (4),
$2i \mu = \log ( {(i-\alpha )}/{(i + \alpha )} )$
. As in item (4),
![]() $\mu \neq 0$
. Suppose
$\mu \neq 0$
. Suppose
![]() $\mu $
is an algebraic number. Then
$\mu $
is an algebraic number. Then
![]() $e^{2i \mu } \in S$
by Theorem 2.4. Now
$e^{2i \mu } \in S$
by Theorem 2.4. Now
![]() $X = \alpha $
and
$X = \alpha $
and
![]() $Y\hspace{-0.5pt} =\hspace{-0.5pt} {(i\hspace{-0.5pt} -\hspace{-0.5pt} \alpha )}/{(i\hspace{-0.5pt} +\hspace{-0.5pt} \alpha )}$
satisfy the equation
$Y\hspace{-0.5pt} =\hspace{-0.5pt} {(i\hspace{-0.5pt} -\hspace{-0.5pt} \alpha )}/{(i\hspace{-0.5pt} +\hspace{-0.5pt} \alpha )}$
satisfy the equation
![]() $P(X,Y)\hspace{-0.5pt} =\hspace{-0.5pt} X^2Y^2\hspace{-0.5pt} +\hspace{-0.5pt} 2X^2Y\hspace{-0.5pt} +\hspace{-0.5pt} X^2\hspace{-0.5pt} -\hspace{-0.5pt} Y^2\hspace{-0.5pt} +\hspace{-0.5pt} 2Y\hspace{-0.5pt} -\hspace{-0.5pt} 1 = 0$
, and hence are algebraically dependent. Theorem 2.3 then implies that
$P(X,Y)\hspace{-0.5pt} =\hspace{-0.5pt} X^2Y^2\hspace{-0.5pt} +\hspace{-0.5pt} 2X^2Y\hspace{-0.5pt} +\hspace{-0.5pt} X^2\hspace{-0.5pt} -\hspace{-0.5pt} Y^2\hspace{-0.5pt} +\hspace{-0.5pt} 2Y\hspace{-0.5pt} -\hspace{-0.5pt} 1 = 0$
, and hence are algebraically dependent. Theorem 2.3 then implies that
![]() ${(i\hspace{-1pt} -\hspace{-1pt} \alpha )}/{(i\hspace{-1pt} +\hspace{-1pt} \alpha )}\hspace{-1pt} \in\hspace{-1pt} U$
, which is a contradiction. So every value of
${(i\hspace{-1pt} -\hspace{-1pt} \alpha )}/{(i\hspace{-1pt} +\hspace{-1pt} \alpha )}\hspace{-1pt} \in\hspace{-1pt} U$
, which is a contradiction. So every value of
![]() $\arctan \alpha $
is transcendental.
$\arctan \alpha $
is transcendental.
(7)
![]() $\sinh \alpha $
. Recall that
$\sinh \alpha $
. Recall that
![]() $\sinh \alpha = \tfrac 12(e^\alpha - e^{-\alpha })$
. By item (1),
$\sinh \alpha = \tfrac 12(e^\alpha - e^{-\alpha })$
. By item (1),
![]() $t = e^\alpha $
is transcendental. Suppose
$t = e^\alpha $
is transcendental. Suppose
![]() $t - {1}/{t} = 2 \mu $
is an algebraic number. This implies that
$t - {1}/{t} = 2 \mu $
is an algebraic number. This implies that
![]() $t = \mu \pm \sqrt {1 - \mu ^2}$
is also algebraic, which is a contradiction. So
$t = \mu \pm \sqrt {1 - \mu ^2}$
is also algebraic, which is a contradiction. So
![]() $\sinh \alpha $
is transcendental.
$\sinh \alpha $
is transcendental.
(8)
![]() $\operatorname {\mathrm {arcsinh}} \alpha $
. We proceed as in item (4). Suppose
$\operatorname {\mathrm {arcsinh}} \alpha $
. We proceed as in item (4). Suppose
![]() $\mu = \operatorname {\mathrm {arcsinh}} \alpha = \log (\alpha + \sqrt {\alpha ^2 + 1})$
is algebraic. By Theorem 2.4,
$\mu = \operatorname {\mathrm {arcsinh}} \alpha = \log (\alpha + \sqrt {\alpha ^2 + 1})$
is algebraic. By Theorem 2.4,
![]() $e^\mu \in S$
. However,
$e^\mu \in S$
. However,
![]() $X = \alpha $
and
$X = \alpha $
and
![]() $Y = \alpha + \sqrt {1+ \alpha ^2}$
satisfy the equation
$Y = \alpha + \sqrt {1+ \alpha ^2}$
satisfy the equation
![]() $P(X,Y) = Y^2 - 2XY -1 = 0$
. Hence, X and Y are algebraically dependent and therefore
$P(X,Y) = Y^2 - 2XY -1 = 0$
. Hence, X and Y are algebraically dependent and therefore
![]() $\alpha + \sqrt {1+ \alpha ^2} \in U$
, which is a contradiction. So
$\alpha + \sqrt {1+ \alpha ^2} \in U$
, which is a contradiction. So
![]() $\operatorname {\mathrm {arcsinh}} \alpha $
is transcendental.
$\operatorname {\mathrm {arcsinh}} \alpha $
is transcendental.
Remark 3.2. In fact, the above argument shows that if
![]() $\alpha $
is in the Mahler class T, then
$\alpha $
is in the Mahler class T, then
![]() $\log \alpha $
is a transcendental number. Additionally, the theorem remains true for the composition of a trigonometric or hyperbolic function with the inverses of the other functions in the corresponding family. For instance, if
$\log \alpha $
is a transcendental number. Additionally, the theorem remains true for the composition of a trigonometric or hyperbolic function with the inverses of the other functions in the corresponding family. For instance, if
![]() $\alpha $
is a Liouville number, then
$\alpha $
is a Liouville number, then
![]() $\sinh (\operatorname {\mathrm {arccosh}} \alpha )$
is transcendental.
$\sinh (\operatorname {\mathrm {arccosh}} \alpha )$
is transcendental.
Remark 3.3. Noting Theorem 2.4, we see that in contrast with Theorem 3.1 and Remark 3.2, it is not true that
![]() $\log s$
is a transcendental number for all members s of the Mahler set S. However, it is of course true for all but a countably infinite number of
$\log s$
is a transcendental number for all members s of the Mahler set S. However, it is of course true for all but a countably infinite number of
![]() $s\in S$
, as the set of algebraic numbers is countably infinite.
$s\in S$
, as the set of algebraic numbers is countably infinite.
Remark 3.4. We conclude by recording that Corollary 6 of [Reference Kumar, Thangadurai and Waldschmift7] implies that
![]() $\exp \alpha $
is a Liouville number for an uncountable number of Liouville numbers
$\exp \alpha $
is a Liouville number for an uncountable number of Liouville numbers
![]() $\alpha $
. Recall Maillet’s result, [Reference Maillet11, Ch. 3], which says that if t is a Liouville number and
$\alpha $
. Recall Maillet’s result, [Reference Maillet11, Ch. 3], which says that if t is a Liouville number and
![]() $R(x)$
is a rational function with rational coefficients, then
$R(x)$
is a rational function with rational coefficients, then
![]() $R(t)$
is a Liouville number. In our case, we use
$R(t)$
is a Liouville number. In our case, we use
![]() $R(t) = \tfrac 12 (t+{1}/{t})$
. It follows from this and [Reference Kumar, Thangadurai and Waldschmift7] that there exists an uncountable set of Liouville numbers
$R(t) = \tfrac 12 (t+{1}/{t})$
. It follows from this and [Reference Kumar, Thangadurai and Waldschmift7] that there exists an uncountable set of Liouville numbers
![]() $\alpha $
such that
$\alpha $
such that
![]() $\sinh \alpha $
is a Liouville number and there exists an uncountable set of Liouville numbers
$\sinh \alpha $
is a Liouville number and there exists an uncountable set of Liouville numbers
![]() $\alpha $
such that
$\alpha $
such that
![]() $\cosh \alpha $
is a Liouville number.
$\cosh \alpha $
is a Liouville number.
Open Question 3.5. If
![]() $\alpha $
is a Liouville number, is
$\alpha $
is a Liouville number, is
![]() $\exp \alpha $
necessarily a Liouville number or a member of the Mahler set U?
$\exp \alpha $
necessarily a Liouville number or a member of the Mahler set U?