Article contents
A SHORT NOTE ON THE FRAME SET OF ODD FUNCTIONS
Published online by Cambridge University Press: 15 August 2018
Abstract
We give a simple argument which shows that Gabor systems consisting of odd
functions of 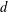 $d$ variables and symplectic lattices of density
$d$ variables and symplectic lattices of density 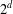 $2^{d}$ cannot constitute a Gabor frame. In the one-dimensional,
separable case, this follows from a more general result of Lyubarskii and
Nes [‘Gabor frames with rational density’, Appl. Comput. Harmon.
Anal.34(3) (2013), 488–494]. We use a different
approach exploiting the algebraic relation between the ambiguity function
and the Wigner distribution as well as their relation given by the
(symplectic) Fourier transform. Also, we do not need the assumption that the
lattice is separable and, hence, new restrictions are added to the full
frame set of odd functions.
$2^{d}$ cannot constitute a Gabor frame. In the one-dimensional,
separable case, this follows from a more general result of Lyubarskii and
Nes [‘Gabor frames with rational density’, Appl. Comput. Harmon.
Anal.34(3) (2013), 488–494]. We use a different
approach exploiting the algebraic relation between the ambiguity function
and the Wigner distribution as well as their relation given by the
(symplectic) Fourier transform. Also, we do not need the assumption that the
lattice is separable and, hence, new restrictions are added to the full
frame set of odd functions.
MSC classification
- Type
- Research Article
- Information
- Bulletin of the Australian Mathematical Society , Volume 98 , Issue 3 , December 2018 , pp. 481 - 493
- Copyright
- © 2018 Australian Mathematical Publishing Association Inc.
Footnotes
The author was supported by the Erwin Schrödinger program of the Austrian Science Fund (FWF): J4100-N32.
References
- 5
- Cited by




