Hostname: page-component-848d4c4894-89wxm Total loading time: 0 Render date: 2024-07-07T06:50:48.294Z Has data issue: false hasContentIssue false
  • English
  • Français

Remarks on the topology of spatial polygon spaces

Published online by Cambridge University Press:  17 April 2009

Yasuhiko Kamiyama
Yasuhiko Kamiyama
Affiliation:
Department of Mathematics, University of the Ryukyus, Nishihara-Cho, Okinawa 903-01, Japan e-mail: kamiyama@sci.u-ryukyu.ac.jp
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let Mn be the “polygon space” introduced by Kirwan and Klyachko. In this paper, we give new results on the topology of Mn for odd n. We determine πq(Mn) (q ≤ n − 3). Then we describe Mn in the oriented cobordism ring 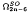. We also give new and elementary proofs of the result on the ring structure of H*(Mn/Sn; Q), where Sn denotes the symmetric group acting naturally on Mn.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 58 , Issue 3 , December 1998 , pp. 373 - 382
Copyright
Copyright © Australian Mathematical Society 1998

References

[1]Bott, R., ‘Nondegenerate critical manifolds’, Ann. of Math. 60 (1954), 248–261.CrossRefGoogle Scholar
[2]Brion, M., ‘Cohomologie équivariante des points semi-stables’, J. Reine Angew. 421 (1991), 125–140.Google Scholar
[3]Griffith, P. and Harris, J., Principles of algebraic geometry (John Wiley and Sons, New York, 1978).Google Scholar
[4]Kamiyama, Y. and Tezuka, M., ‘Topology and geometry of equilateral polygon linkages in the Euclidean plane’, (preprint).Google Scholar
[5]Kamiyama, Y., ‘The homology of singular polygon spaces’, (preprint).Google Scholar
[6]Kirwan, F., The cohomology of quotients in symplectic and algebraic geometry, Mathematical Notes 31 (Princeton University Press, 1984).Google Scholar
[7]Kirwan, F., ‘Cohomology rings of moduli spaces of bundles over Riemannian surfaces’, J. Amer. Math. Soc. 5 (1992), 853–906.CrossRefGoogle Scholar
[8]Klyachko, A., ‘Spatial polygons and stable configurations of points in the projective line’, in Algebraic geometry and its applications, Aspects of Mathematics 25 (Vieweg, Braunschweig, 1994), pp. 67–84.CrossRefGoogle Scholar
[9]Lawson, H.B. and Michelsohn, M., Spin geometry (Princeton University Press, Princeton, N.J., 1989).Google Scholar
[10]Oshanin, S., ‘The signature of SU-manifolds’, Mat. Zametki 13 (1973), 97–102: Math. Notes, 13 (1973), 57–60.Google Scholar