Article contents
PROOF OF TWO CONJECTURES ON SUPERCONGRUENCES INVOLVING CENTRAL BINOMIAL COEFFICIENTS
Published online by Cambridge University Press: 13 February 2020
Abstract
In this note we use some 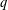 $q$-congruences proved by the method of ‘creative microscoping’ to prove two conjectures on supercongruences involving central binomial coefficients. In particular, we confirm the
$q$-congruences proved by the method of ‘creative microscoping’ to prove two conjectures on supercongruences involving central binomial coefficients. In particular, we confirm the 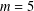 $m=5$ case of Conjecture 1.1 of Guo [‘Some generalizations of a supercongruence of Van Hamme’, Integral Transforms Spec. Funct.28 (2017), 888–899].
$m=5$ case of Conjecture 1.1 of Guo [‘Some generalizations of a supercongruence of Van Hamme’, Integral Transforms Spec. Funct.28 (2017), 888–899].
MSC classification
- Type
- Research Article
- Information
- Bulletin of the Australian Mathematical Society , Volume 102 , Issue 3 , December 2020 , pp. 360 - 364
- Copyright
- © 2020 Australian Mathematical Publishing Association Inc.
Footnotes
The second author was partially supported by the National Natural Science Foundation of China (Grant No. 11771175).
References
- 4
- Cited by





