Article contents
ON THE TOTAL DISTANCE AND DIAMETER OF GRAPHS
Published online by Cambridge University Press: 03 May 2018
Abstract
The total distance (or Wiener index) of a connected graph 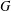 $G$ is the sum of all distances between unordered pairs of vertices of
$G$ is the sum of all distances between unordered pairs of vertices of 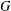 $G$. DeLaViña and Waller [‘Spanning trees with many leaves and average distance’, Electron. J. Combin.15(1) (2008), R33, 14 pp.] conjectured in 2008 that if
$G$. DeLaViña and Waller [‘Spanning trees with many leaves and average distance’, Electron. J. Combin.15(1) (2008), R33, 14 pp.] conjectured in 2008 that if 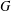 $G$ has diameter
$G$ has diameter 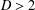 $D>2$ and order
$D>2$ and order 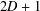 $2D+1$, then the total distance of
$2D+1$, then the total distance of 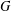 $G$ is at most the total distance of the cycle of the same order. In this note, we prove that this conjecture is true for 2-connected graphs.
$G$ is at most the total distance of the cycle of the same order. In this note, we prove that this conjecture is true for 2-connected graphs.
- Type
- Research Article
- Information
- Copyright
- © 2018 Australian Mathematical Publishing Association Inc.
References
- 2
- Cited by




