Article contents
ON THE ORDER OF ARC-STABILISERS IN ARC-TRANSITIVE GRAPHS, II
Published online by Cambridge University Press: 02 August 2012
Abstract
Let 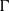 $\Gamma $ be a
$\Gamma $ be a 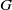 $G$-vertex-transitive graph and let
$G$-vertex-transitive graph and let 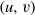 $(u,v)$ be an arc of
$(u,v)$ be an arc of 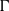 $\Gamma $. It is known that if the local action
$\Gamma $. It is known that if the local action 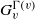 $G_v^{\Gamma (v)}$ (the permutation group induced by
$G_v^{\Gamma (v)}$ (the permutation group induced by 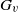 $G_v$ on
$G_v$ on 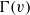 $\Gamma (v)$) is permutation isomorphic to the dihedral group of degree four, then either
$\Gamma (v)$) is permutation isomorphic to the dihedral group of degree four, then either 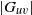 $|G_{uv}|$ is ‘small’ with respect to the order of
$|G_{uv}|$ is ‘small’ with respect to the order of 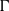 $\Gamma $ or
$\Gamma $ or 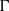 $\Gamma $is one of a family of well-understood graphs. In this paper, we generalise this result to a wider class of local actions.
$\Gamma $is one of a family of well-understood graphs. In this paper, we generalise this result to a wider class of local actions.
MSC classification
- Type
- Research Article
- Information
- Copyright
- Copyright © 2012 Australian Mathematical Publishing Association Inc.
References
- 7
- Cited by




