Hostname: page-component-76fb5796d-r6qrq Total loading time: 0 Render date: 2024-04-27T07:20:10.512Z Has data issue: false hasContentIssue false
  • English
  • Français

ON THE LIMIT SET OF A COMPLEX HYPERBOLIC TRIANGLE GROUP

Part of: Other groups of matrices Lie groups

Published online by Cambridge University Press:  02 February 2024

MENGQI SHI Open the ORCID record for MENGQI SHI [Opens in a new window]  and
JIEYAN WANG
MENGQI SHI*
Affiliation:
School of Mathematics, Hunan University, Changsha 410082, PR China
JIEYAN WANG
Affiliation:
School of Mathematics, Hunan University, Changsha 410082, PR China e-mail: jywang@hnu.edu.cn
*
e-mail: mqshi@hnu.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 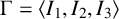$\Gamma =\langle I_{1}, I_{2}, I_{3}\rangle $ be the complex hyperbolic 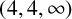$(4,4,\infty )$ triangle group with 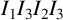$I_1I_3I_2I_3$ being unipotent. We show that the limit set of 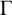$\Gamma $ is connected and the closure of a countable union of 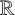$\mathbb {R}$-circles.

Keywords

complex hyperbolic triangle groupslimit sets

MSC classification

Primary: 22E40: Discrete subgroups of Lie groups
Secondary: 20H10: Fuchsian groups and their generalizations
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , First View , pp. 1 - 8
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

This work was partially supported by the NSFC (Grant No. 12271148).

References

Acosta, M., ‘On the limit set of a spherical CR uniformization’, Algebr. Geom. Topol. 22 (2022), 3305–3325.CrossRefGoogle Scholar
Falbel, E., Guilloux, A. and Will, P., ‘Slim curves, limit sets and spherical CR uniformisations’, Preprint, 2022, arXiv:2205.08797.Google Scholar
Falbel, E. and Parker, J. R., ‘The geometry of the Eisenstein–Picard modular group’, Duke Math. J. 131 (2006), 249–289.CrossRefGoogle Scholar
Falbel, E. and Zocca, V., ‘A Poincaré’s polyhedron theorem for complex hyperbolic geometry’, J. reine angew. Math. 516 (1999), 133–158.CrossRefGoogle Scholar
Goldman, W. M., Complex Hyperbolic Geometry, Oxford Mathematical Monographs (Oxford University Press, Oxford, 1999).CrossRefGoogle Scholar
Jiang, Y., Wang, J. and Xie, B., ‘A uniformizable spherical CR structure on a two-cusped hyperbolic 3-manifold’, Algebr. Geom. Topol. 23 (2023), 4143–4184.CrossRefGoogle Scholar
Parker, J. R., Notes on Complex Hyperbolic Geometry (University of Durham, Durham, 2003). https://maths.dur.ac.uk/users/j.r.parker/img/NCHG.pdf.Google Scholar
Pratoussevitch, A., ‘Traces in complex hyperbolic triangle groups’, Geom. Dedicata 111 (2005), 159–185.CrossRefGoogle Scholar
Schwartz, R. E., ‘Complex hyperbolic triangle groups’, in: Proceedings of the International Congress of Mathematicians, Beijing, 2002, Volume II: Invited Lectures (ed. Li, T.) (Higher Education Press, Beijing, 2002), 339–350.Google Scholar
Schwartz, R. E., ‘Real hyperbolic on the outside, complex hyperbolic on the inside’, Invent. Math. 151 (2003), 221–295.CrossRefGoogle Scholar
Takeuchi, K., ‘Arithmetic triangle groups’, J. Math. Soc. Japan 29 (1977), 91–106.CrossRefGoogle Scholar