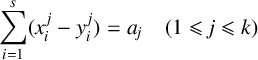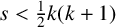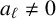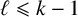1 Introduction
Sitting squarely at the interface of harmonic analysis and analytic number theory, systems of diagonal equations have long attracted a significant amount of attention. In particular, thanks to the resolution of the main conjecture associated with Vinogradov’s mean value theorem by Wooley [Reference Wooley10] and Bourgain et al. [Reference Bourgain, Demeter and Guth2] (see also [Reference Wooley11]), we now have essentially sharp upper bounds for the number of integer solutions of systems of equations of Vinogradov type.
For integral
![]() $s, k$
, denote by
$s, k$
, denote by
![]() $J_{s,k}(X)$
the number of solutions
$J_{s,k}(X)$
the number of solutions
![]() $\mathbf{x}, \mathbf{y} \in \mathbb Z^{s} \cap [-X,X]^{s}$
satisfying
$\mathbf{x}, \mathbf{y} \in \mathbb Z^{s} \cap [-X,X]^{s}$
satisfying
 $$ \begin{align} \sum_{i=1}^{s} (x_{i}^{\,j}-y_{i}^{\,j}) = 0 \quad (1 \leqslant j \leqslant k). \end{align} $$
$$ \begin{align} \sum_{i=1}^{s} (x_{i}^{\,j}-y_{i}^{\,j}) = 0 \quad (1 \leqslant j \leqslant k). \end{align} $$
We remark for future reference that by transitioning to exponential sums, the quantity
![]() $J_{s,k}(X)$
may be defined also for noninteger positive s (see (2.4)). In this notation, [Reference Bourgain, Demeter and Guth2, Theorem 1.1] (see also [Reference Wooley11, Corollary 1.3]) shows that for all positive numbers s and all
$J_{s,k}(X)$
may be defined also for noninteger positive s (see (2.4)). In this notation, [Reference Bourgain, Demeter and Guth2, Theorem 1.1] (see also [Reference Wooley11, Corollary 1.3]) shows that for all positive numbers s and all
![]() $k \in \mathbb N$
,
$k \in \mathbb N$
,
The second term in (1.2), dominant when
![]() $s> \tfrac 12k(k+1)$
, conforms with the circle method heuristic which states that a system of equations in n variables and of total degree K should have
$s> \tfrac 12k(k+1)$
, conforms with the circle method heuristic which states that a system of equations in n variables and of total degree K should have
![]() $\sim c X^{n-K}$
solutions over the integers of size at most X, where the factor c encodes the density of solutions of the underlying system over all completions of
$\sim c X^{n-K}$
solutions over the integers of size at most X, where the factor c encodes the density of solutions of the underlying system over all completions of
![]() $\mathbb Q$
. Indeed, in the case of (1.1), such an asymptotic formula is readily established for
$\mathbb Q$
. Indeed, in the case of (1.1), such an asymptotic formula is readily established for
![]() $s> \tfrac 12k(k+1)$
by a classical application of the Hardy–Littlewood method (see [Reference Vaughan7, Ch. 7]). Moreover, these methods are robust with respect to small modifications to the system (1.1) such as nontrivial coefficients or a nonvanishing expression on the right-hand side of (1.1).
$s> \tfrac 12k(k+1)$
by a classical application of the Hardy–Littlewood method (see [Reference Vaughan7, Ch. 7]). Moreover, these methods are robust with respect to small modifications to the system (1.1) such as nontrivial coefficients or a nonvanishing expression on the right-hand side of (1.1).
When s is smaller than
![]() $\tfrac 12k(k+1)$
, the circle method heuristic fails for (1.1), as we have to allow for the existence of diagonal solutions in which the variables
$\tfrac 12k(k+1)$
, the circle method heuristic fails for (1.1), as we have to allow for the existence of diagonal solutions in which the variables
![]() $(x_{1}, x_{2}, \ldots , x_{s})$
are a permutation of
$(x_{1}, x_{2}, \ldots , x_{s})$
are a permutation of
![]() $(y_{1}, y_{2},\ldots , y_{s})$
. The contribution of these solutions amounts to
$(y_{1}, y_{2},\ldots , y_{s})$
. The contribution of these solutions amounts to
![]() $s!X^{s}$
, so it is natural to expect an asymptotic formula of the shape
$s!X^{s}$
, so it is natural to expect an asymptotic formula of the shape
to hold in the subcritical range. Adventurous souls might even go as far as to conjecture that the nondiagonal contribution to the mean value
![]() $J_{s,k}(X)$
should be no larger than
$J_{s,k}(X)$
should be no larger than
![]() $O(X^{\varepsilon }(1 + X^{2s-k(k+1)/2}))$
, based on an expectation that the circle method heuristic should continue to be valid in that setting. Somewhat frustratingly, however, we are able to establish (1.3) only in the range
$O(X^{\varepsilon }(1 + X^{2s-k(k+1)/2}))$
, based on an expectation that the circle method heuristic should continue to be valid in that setting. Somewhat frustratingly, however, we are able to establish (1.3) only in the range
![]() $s \leqslant k+1$
(see [Reference Vaughan and Wooley8, Theorem 1]), which falls far short of the conjectured range
$s \leqslant k+1$
(see [Reference Vaughan and Wooley8, Theorem 1]), which falls far short of the conjectured range
![]() $s<\tfrac 12k(k+1)$
.
$s<\tfrac 12k(k+1)$
.
The purpose of this note is to study an inhomogeneous version of the system (1.1) that does not allow for diagonal contributions. For
![]() $s, k \in \mathbb N$
and
$s, k \in \mathbb N$
and
![]() $a_{1}, \ldots , a_{k} \in \mathbb Z$
, write
$a_{1}, \ldots , a_{k} \in \mathbb Z$
, write
![]() $J_{s,k}(X;\mathbf{a})$
for the number of
$J_{s,k}(X;\mathbf{a})$
for the number of
![]() $\mathbf{x}, \mathbf{y} \in \mathbb Z^{s} \cap [-X,X]^{s}$
satisfying the system of equations
$\mathbf{x}, \mathbf{y} \in \mathbb Z^{s} \cap [-X,X]^{s}$
satisfying the system of equations
 $$ \begin{align} \sum_{i=1}^{s} (x_{i}^{\,j}-y_{i}^{\,j}) = a_{j} \quad (1 \leqslant j \leqslant k). \end{align} $$
$$ \begin{align} \sum_{i=1}^{s} (x_{i}^{\,j}-y_{i}^{\,j}) = a_{j} \quad (1 \leqslant j \leqslant k). \end{align} $$
Systems of this or similar types have recently arisen in a range of different contexts (for example, [Reference Baker, Munsch and Shparlinski1, Reference Chen, Kerr, Maynard and Shparlinski4, Reference Dendrinos, Hughes and Vitturi5]). It follows easily by a standard application from the triangle inequality that
in the subcritical range. We show that for most
![]() $\mathbf{a}$
, we can do better.
$\mathbf{a}$
, we can do better.
Theorem 1.1. Suppose that
![]() $k \geqslant 2$
and
$k \geqslant 2$
and
![]() $\mathbf{a} \in \mathbb Z^{k} \setminus \{\boldsymbol 0\}$
. Let
$\mathbf{a} \in \mathbb Z^{k} \setminus \{\boldsymbol 0\}$
. Let
![]() $\ell \in \{1, \ldots , k\}$
be the smallest integer for which
$\ell \in \{1, \ldots , k\}$
be the smallest integer for which
![]() $a_{\ell } \neq 0$
. Then for any integer
$a_{\ell } \neq 0$
. Then for any integer
![]() $s < \tfrac 12 k(k+1)$
and any
$s < \tfrac 12 k(k+1)$
and any
![]() $\varepsilon> 0$
,
$\varepsilon> 0$
,
where
By a brief computation, the first term in (1.6) dominates for
![]() $s=\tfrac 12 k(k+1) - 1$
as soon as
$s=\tfrac 12 k(k+1) - 1$
as soon as
![]() $a_{\ell } \neq 0$
for some
$a_{\ell } \neq 0$
for some
![]() $\ell \leqslant k-\tfrac 12(\sqrt {2k^{2}+2k+1}-1)$
. Hence, we have the following simple consequence of Theorem 1.1.
$\ell \leqslant k-\tfrac 12(\sqrt {2k^{2}+2k+1}-1)$
. Hence, we have the following simple consequence of Theorem 1.1.
Corollary 1.2. Suppose that
![]() $k \geqslant 2$
and assume that
$k \geqslant 2$
and assume that
![]() $a_{\ell } \neq 0$
for some
$a_{\ell } \neq 0$
for some
Then for any integer
![]() $s \leqslant \tfrac 12 k(k+1)-1$
and any
$s \leqslant \tfrac 12 k(k+1)-1$
and any
![]() $\varepsilon> 0$
,
$\varepsilon> 0$
,
Here, one can compute
 $$ \begin{align*} k-\frac12(\sqrt{2k^{2}+2k+1}-1) &= \bigg(1-\frac{1}{\sqrt 2}\bigg) \bigg(k + \frac12 \bigg) + O(1/k)\\&= 0.292\ldots\cdot k + 0.146\ldots + O(1/k). \end{align*} $$
$$ \begin{align*} k-\frac12(\sqrt{2k^{2}+2k+1}-1) &= \bigg(1-\frac{1}{\sqrt 2}\bigg) \bigg(k + \frac12 \bigg) + O(1/k)\\&= 0.292\ldots\cdot k + 0.146\ldots + O(1/k). \end{align*} $$
It may be worth pointing out that we do not expect to obtain power savings over the bound (1.5) when s is at or beyond the critical point and
![]() $|a_{j}| \leqslant 2sX^{j}$
for
$|a_{j}| \leqslant 2sX^{j}$
for
![]() $1 \leqslant j \leqslant k$
, since at that point, the contribution from a major arcs analysis will be of size
$1 \leqslant j \leqslant k$
, since at that point, the contribution from a major arcs analysis will be of size
![]() $\gg X^{2s-k(k+1)}$
(see [Reference Vaughan7, Ch. 7] for details). In this sense, the range
$\gg X^{2s-k(k+1)}$
(see [Reference Vaughan7, Ch. 7] for details). In this sense, the range
![]() $s \leqslant \tfrac 12k(k+1) -1$
is optimal.
$s \leqslant \tfrac 12k(k+1) -1$
is optimal.
The proof of Theorem 1.1 relies crucially on the absence of translation invariance in the system (1.4). For this reason, our result becomes gradually weaker as the system acquires larger translation-invariant subsystems, up to the point when
![]() $\mathbf{a} = (0, \ldots , 0, a_{k})^{t}$
, where we have
$\mathbf{a} = (0, \ldots , 0, a_{k})^{t}$
, where we have
![]() $\ell =k$
and
$\ell =k$
and
![]() $\eta _{s,k}(k)=0$
. At this point, the entire system becomes translation-invariant, so we fail to make any progress beyond the trivial bound (1.5).
$\eta _{s,k}(k)=0$
. At this point, the entire system becomes translation-invariant, so we fail to make any progress beyond the trivial bound (1.5).
Our strategy transfers to several other settings, but in the interest of a slick presentation, we have opted to focus our attention on the inhomogeneous Vinogradov system, since this seems to be by far the most relevant example. However, we discuss some possible extensions of our result as well as some of its limitations in the final section.
Notation. We denote the unit torus by
![]() $\mathbb T = \mathbb R /\mathbb Z$
. Throughout, the letter
$\mathbb T = \mathbb R /\mathbb Z$
. Throughout, the letter
![]() $\varepsilon $
will be used to denote an arbitrary positive number. We adopt the convention that whenever
$\varepsilon $
will be used to denote an arbitrary positive number. We adopt the convention that whenever
![]() $\varepsilon $
appears in a statement, the statement holds for all
$\varepsilon $
appears in a statement, the statement holds for all
![]() $\varepsilon>0$
. Finally, we take X to be a large positive number which, just like the implicit constants in the notations of Landau and Vinogradov, is permitted to depend at most on s, k and
$\varepsilon>0$
. Finally, we take X to be a large positive number which, just like the implicit constants in the notations of Landau and Vinogradov, is permitted to depend at most on s, k and
![]() $\varepsilon $
.
$\varepsilon $
.
2 Proof of the main theorem
In our proof, we employ a strategy inspired by work of Wooley [Reference Wooley9] to understand systems with incomplete translation-invariant structure. Our first step is to bound
![]() $J_{s,k}(X;\mathbf{a})$
in terms of a different quantity which will be easier to handle. Define polynomials
$J_{s,k}(X;\mathbf{a})$
in terms of a different quantity which will be easier to handle. Define polynomials
![]() $p_{j}$
by setting
$p_{j}$
by setting
 $$ \begin{align} p_{j}(h) = \sum_{m=1}^{j} \binom{j}{m} a_{m}h^{{\kern1.3pt}j-m} \quad (1 \leqslant j \leqslant k). \end{align} $$
$$ \begin{align} p_{j}(h) = \sum_{m=1}^{j} \binom{j}{m} a_{m}h^{{\kern1.3pt}j-m} \quad (1 \leqslant j \leqslant k). \end{align} $$
Write
![]() $H_{s,k}(X;\mathbf{a})$
for the number of
$H_{s,k}(X;\mathbf{a})$
for the number of
![]() $\mathbf{z}, \mathbf{w} \in \mathbb Z^{s} \cap [-2X,2X]^{s}$
and
$\mathbf{z}, \mathbf{w} \in \mathbb Z^{s} \cap [-2X,2X]^{s}$
and
![]() $h \in \mathbb Z \cap [-X,X]$
satisfying the system of equations
$h \in \mathbb Z \cap [-X,X]$
satisfying the system of equations
 $$ \begin{align} \sum_{i=1}^{s} (z_{i}^{\,j}-w_{i}^{\,j}) = p_{j}(h) \quad (1 \leqslant j \leqslant k). \end{align} $$
$$ \begin{align} \sum_{i=1}^{s} (z_{i}^{\,j}-w_{i}^{\,j}) = p_{j}(h) \quad (1 \leqslant j \leqslant k). \end{align} $$
Lemma 2.1. We have
Proof. Suppose that
![]() $(\mathbf{x}, \mathbf{y})$
is a solution to (1.4), and fix a parameter
$(\mathbf{x}, \mathbf{y})$
is a solution to (1.4), and fix a parameter
![]() $h \in \mathbb Z$
. It follows from the binomial theorem that
$h \in \mathbb Z$
. It follows from the binomial theorem that
![]() $(\mathbf{x},\mathbf{y})$
is also a solution of the shifted system
$(\mathbf{x},\mathbf{y})$
is also a solution of the shifted system
 $$ \begin{align*} \sum_{i=1}^{s} ((x_{i}+h)^{\,j}-(y_{i}+h)^{\,j}) = p_{j}(h) \quad (1 \leqslant j \leqslant k). \end{align*} $$
$$ \begin{align*} \sum_{i=1}^{s} ((x_{i}+h)^{\,j}-(y_{i}+h)^{\,j}) = p_{j}(h) \quad (1 \leqslant j \leqslant k). \end{align*} $$
If now
![]() $|h| \leqslant X$
, then the number of such solutions
$|h| \leqslant X$
, then the number of such solutions
![]() $\mathbf{x}, \mathbf{y} \in \mathbb Z^{s} \cap [-X,X]^{s}$
is certainly no larger than the number of
$\mathbf{x}, \mathbf{y} \in \mathbb Z^{s} \cap [-X,X]^{s}$
is certainly no larger than the number of
![]() $\mathbf{z}, \mathbf{w} \in \mathbb Z^{s} \cap [-2X,2X]^{s}$
satisfying (2.2) with that particular value of h. The desired conclusion now follows upon summing over all
$\mathbf{z}, \mathbf{w} \in \mathbb Z^{s} \cap [-2X,2X]^{s}$
satisfying (2.2) with that particular value of h. The desired conclusion now follows upon summing over all
![]() $|h| \leqslant X$
.
$|h| \leqslant X$
.
Next, we write
![]() $H_{s,k}(X;\mathbf{a})$
in terms of mean values over exponential sums. Set
$H_{s,k}(X;\mathbf{a})$
in terms of mean values over exponential sums. Set
 $$ \begin{align*} f_{k}({\boldsymbol \alpha};X) = \sum_{|x| \leqslant X} e({\alpha}_{1} x + \cdots + {\alpha}_{k} x^{k}) \end{align*} $$
$$ \begin{align*} f_{k}({\boldsymbol \alpha};X) = \sum_{|x| \leqslant X} e({\alpha}_{1} x + \cdots + {\alpha}_{k} x^{k}) \end{align*} $$
and
 $$ \begin{align} g_{k}({\boldsymbol \alpha};X) = \sum_{|x| \leqslant X} e({\alpha}_{1} p_{1}(h) + \cdots + {\alpha}_{k} p_{k}(h)), \end{align} $$
$$ \begin{align} g_{k}({\boldsymbol \alpha};X) = \sum_{|x| \leqslant X} e({\alpha}_{1} p_{1}(h) + \cdots + {\alpha}_{k} p_{k}(h)), \end{align} $$
and recall that in this notation, we have
Similarly, it follows from standard orthogonality relations that we may write
From the definition of
![]() $p_{j}$
in (2.1), we see that
$p_{j}$
in (2.1), we see that
![]() $g_{k}({\boldsymbol \alpha };X)$
is an exponential sum of degree at most
$g_{k}({\boldsymbol \alpha };X)$
is an exponential sum of degree at most
![]() $k-1$
; however, its degree may be lower depending on the values of the coefficients
$k-1$
; however, its degree may be lower depending on the values of the coefficients
![]() $a_{1}, a_{2}, \ldots , a_{k}$
. In particular, recalling that
$a_{1}, a_{2}, \ldots , a_{k}$
. In particular, recalling that
![]() $\ell \in \{1, \ldots , k\}$
denotes the smallest integer for which
$\ell \in \{1, \ldots , k\}$
denotes the smallest integer for which
![]() $a_{\ell } \neq 0$
, we discern from (2.1) that
$a_{\ell } \neq 0$
, we discern from (2.1) that
Thus,
![]() $g_{k}({\boldsymbol \alpha };X)$
is an exponential sum containing
$g_{k}({\boldsymbol \alpha };X)$
is an exponential sum containing
![]() $k-\ell $
integer polynomials with degrees
$k-\ell $
integer polynomials with degrees
![]() $1, \ldots ,k-\ell $
.
$1, \ldots ,k-\ell $
.
We now apply Hölder’s inequality to (2.5) and find that
 $$ \begin{align} H_{s,k}(X;\mathbf{a}) \leqslant \bigg(\int_{\mathbb T^{k}} |f_{k}({\boldsymbol \alpha};2X)|^{k(k+1)} \,d {\boldsymbol \alpha}\bigg)^{{2s}/{k(k+1)}} \bigg(\int_{\mathbb T^{k}} |g_{k}({\boldsymbol \alpha};X)|^{2{\sigma}}\,d {\boldsymbol \alpha}\bigg)^{1/(2{\sigma})}, \end{align} $$
$$ \begin{align} H_{s,k}(X;\mathbf{a}) \leqslant \bigg(\int_{\mathbb T^{k}} |f_{k}({\boldsymbol \alpha};2X)|^{k(k+1)} \,d {\boldsymbol \alpha}\bigg)^{{2s}/{k(k+1)}} \bigg(\int_{\mathbb T^{k}} |g_{k}({\boldsymbol \alpha};X)|^{2{\sigma}}\,d {\boldsymbol \alpha}\bigg)^{1/(2{\sigma})}, \end{align} $$
where
Clearly, the first integral in (2.7) is
![]() $J_{k(k+1)/2,k}(2X)$
. Moreover, from (2.3), (2.1) and (2.6), it follows via an integer change of variables on
$J_{k(k+1)/2,k}(2X)$
. Moreover, from (2.3), (2.1) and (2.6), it follows via an integer change of variables on
![]() ${\boldsymbol \alpha }$
together with the periodicity of the exponential sums that
${\boldsymbol \alpha }$
together with the periodicity of the exponential sums that
Consequently, upon inserting the bound (1.2) from [Reference Bourgain, Demeter and Guth2, Theorem 1.1], we conclude that
 $$ \begin{align*} H_{s,k}(X;\mathbf{a}) &\ll (J_{k(k+1)/2,k}(2X))^{{2s}/{k(k+1)}} (J_{{\sigma},k-\ell}(X))^{1/(2{\sigma})}\\ &\ll X^{\varepsilon} (X^{k(k+1)/2})^{{2s}/{k(k+1)}} (X^{\sigma} + X^{2{\sigma} - (k-\ell)(k-\ell+1)/2})^{1/(2{\sigma})}\\ &\ll X^{s + \varepsilon} (X^{1/2} + X^{1-(k-\ell)(k-\ell+1)/(4{\sigma})} ). \end{align*} $$
$$ \begin{align*} H_{s,k}(X;\mathbf{a}) &\ll (J_{k(k+1)/2,k}(2X))^{{2s}/{k(k+1)}} (J_{{\sigma},k-\ell}(X))^{1/(2{\sigma})}\\ &\ll X^{\varepsilon} (X^{k(k+1)/2})^{{2s}/{k(k+1)}} (X^{\sigma} + X^{2{\sigma} - (k-\ell)(k-\ell+1)/2})^{1/(2{\sigma})}\\ &\ll X^{s + \varepsilon} (X^{1/2} + X^{1-(k-\ell)(k-\ell+1)/(4{\sigma})} ). \end{align*} $$
The proof of Theorem 1.1 is now complete upon recalling Lemma 2.1 and inserting the value of
![]() ${\sigma }$
from (2.8).
${\sigma }$
from (2.8).
3 Further discussion: Generalisations and limitations
It is natural to ask in what ways the proof of Theorem 1.1 may be generalised. As mentioned in the introduction, a close reading of our methods reveals that the translation-invariant structure of the system does indeed play a crucial role in our arguments. Consequently, there is little hope to extend our results to incomplete Vinogradov systems such as those considered in [Reference Brandes and Wooley3] without fundamentally different ideas.
However, the idea underpinning the proof of Theorem 1.1 is quite general, and can be used to bound the number of solutions of the inhomogeneous analogues of other translation-invariant systems, including multidimensional ones such as those considered in [Reference Guo and Zorin-Kranich6]. Indeed, beyond a sharp mean value estimate for such systems in the subcritical range, we only need a nontrivial bound for a derived mean value over a family of ‘shifting polynomials’ analogous to the polynomials
![]() $p_{j}$
occurring in Lemma 2.1. Owing to its genesis via shifting the variables, this derived mean value can be seen to be of the same general shape as the original one (but with lower degree), and therefore a similar mean value estimate can usually be applied, leading to a nontrivial bound as soon as at least one of the shifting polynomials is nonconstant. Alternatively, one could also use square-root cancellation at the second moment (Plancherel’s theorem) and interpolate with trivial bounds at
$p_{j}$
occurring in Lemma 2.1. Owing to its genesis via shifting the variables, this derived mean value can be seen to be of the same general shape as the original one (but with lower degree), and therefore a similar mean value estimate can usually be applied, leading to a nontrivial bound as soon as at least one of the shifting polynomials is nonconstant. Alternatively, one could also use square-root cancellation at the second moment (Plancherel’s theorem) and interpolate with trivial bounds at
![]() $L^{\infty }$
to obtain cancellation at all moments greater than
$L^{\infty }$
to obtain cancellation at all moments greater than
![]() $2$
. In this manner, our method shows that the numbers of solutions of most inhomogeneous translation-invariant systems of equations are measurably smaller than the corresponding bounds for their homogeneous analogues for all even moments in the subcritical range.
$2$
. In this manner, our method shows that the numbers of solutions of most inhomogeneous translation-invariant systems of equations are measurably smaller than the corresponding bounds for their homogeneous analogues for all even moments in the subcritical range.
A different direction for generalisations is that in which the variables
![]() $x_{i}, y_{i}$
are restricted to some subset
$x_{i}, y_{i}$
are restricted to some subset
![]() ${\mathcal X} \subseteq [-X,X]\cap \mathbb Z$
. Fixing such a set
${\mathcal X} \subseteq [-X,X]\cap \mathbb Z$
. Fixing such a set
![]() ${\mathcal X}$
as well as a set of shifting variables
${\mathcal X}$
as well as a set of shifting variables
![]() ${\mathcal H} \subset [-X,X]\cap \mathbb Z$
, put
${\mathcal H} \subset [-X,X]\cap \mathbb Z$
, put
![]() $J_{s,k}({\mathcal X};\mathbf{a})$
for the number of
$J_{s,k}({\mathcal X};\mathbf{a})$
for the number of
![]() $\mathbf{x}, \mathbf{y} \in {\mathcal X}^{s}$
satisfying (1.4), and write
$\mathbf{x}, \mathbf{y} \in {\mathcal X}^{s}$
satisfying (1.4), and write
![]() $H_{s,k}({\mathcal X}, {\mathcal H};\mathbf{a})$
for the number of
$H_{s,k}({\mathcal X}, {\mathcal H};\mathbf{a})$
for the number of
![]() $\mathbf{x}, \mathbf{y} \in ({\mathcal X}+{\mathcal H})^{s}$
and
$\mathbf{x}, \mathbf{y} \in ({\mathcal X}+{\mathcal H})^{s}$
and
![]() $h \in {\mathcal H}$
solving the system (2.2). Then an inspection of the proof of Lemma 2.1 shows that
$h \in {\mathcal H}$
solving the system (2.2). Then an inspection of the proof of Lemma 2.1 shows that
Since it follows from [Reference Bourgain, Demeter and Guth2, Theorem 1.2] and [Reference Wooley11, Theorem 1.1] that
the same argument as above leads mutatis mutandis to the following conclusion.
Theorem 3.1. Suppose that
![]() $k \geqslant 2$
and
$k \geqslant 2$
and
![]() $\mathbf{a} \in \mathbb Z^{k} \setminus \{\boldsymbol 0\}$
. Let
$\mathbf{a} \in \mathbb Z^{k} \setminus \{\boldsymbol 0\}$
. Let
![]() $\ell \in \{1, \ldots , k\}$
be the smallest integer for which
$\ell \in \{1, \ldots , k\}$
be the smallest integer for which
![]() $a_{\ell } \neq 0$
. Moreover, fix a set
$a_{\ell } \neq 0$
. Moreover, fix a set
![]() ${\mathcal X} \subseteq [-X,X] \cap \mathbb Z$
. Then for any integer
${\mathcal X} \subseteq [-X,X] \cap \mathbb Z$
. Then for any integer
![]() $s < \tfrac 12 k(k+1)$
, any set
$s < \tfrac 12 k(k+1)$
, any set
![]() ${\mathcal H} \subseteq [-X,X] \cap \mathbb Z$
and any
${\mathcal H} \subseteq [-X,X] \cap \mathbb Z$
and any
![]() $\varepsilon> 0$
,
$\varepsilon> 0$
,
where
![]() $\eta _{s,k}(\ell )$
is as in Theorem 1.1.
$\eta _{s,k}(\ell )$
is as in Theorem 1.1.
From the point of view of harmonic analysis, it would be of interest to have an analogue of Theorem 1.1 involving systems of the type (1.4) in which each solution is counted by a complex weight. Such situations arise habitually in the context of restriction and extension operators. For a given complex-valued sequence
![]() $({\mathfrak c}_{n})_{n \in \mathbb Z}$
, one defines the truncated extension operator along the moment curve
$({\mathfrak c}_{n})_{n \in \mathbb Z}$
, one defines the truncated extension operator along the moment curve
![]() $(t,t^{2}, \ldots , t^{k}) \subset \mathbb R^{k}$
via
$(t,t^{2}, \ldots , t^{k}) \subset \mathbb R^{k}$
via
 $$ \begin{align*} E_{X}{\mathfrak c}({\boldsymbol \alpha}) = \sum_{|x| \leqslant X} {\mathfrak c}_{x} e({\alpha}_{1} x + \cdots + {\alpha}_{k} x^{k}), \end{align*} $$
$$ \begin{align*} E_{X}{\mathfrak c}({\boldsymbol \alpha}) = \sum_{|x| \leqslant X} {\mathfrak c}_{x} e({\alpha}_{1} x + \cdots + {\alpha}_{k} x^{k}), \end{align*} $$
so that
![]() . In this notation, the conclusion of [Reference Bourgain, Demeter and Guth2, Theorem 1.2] and [Reference Wooley11, Theorem 1.1] reads
. In this notation, the conclusion of [Reference Bourgain, Demeter and Guth2, Theorem 1.2] and [Reference Wooley11, Theorem 1.1] reads
Consider the Fourier transform of
![]() $|E_{X}{\mathfrak c}({\boldsymbol \alpha })|^{2s}$
, which is given by
$|E_{X}{\mathfrak c}({\boldsymbol \alpha })|^{2s}$
, which is given by
so that in particular
![]() $ \|E_{X} {\mathfrak c}\|^{2s}_{L^{2s}(\mathbb T^{k})} = \Phi (\boldsymbol 0)$
. Of course, it follows directly via the triangle inequality that
$ \|E_{X} {\mathfrak c}\|^{2s}_{L^{2s}(\mathbb T^{k})} = \Phi (\boldsymbol 0)$
. Of course, it follows directly via the triangle inequality that
![]() $|\Phi (\mathbf{n})| \leqslant \Phi (\boldsymbol 0)$
for all
$|\Phi (\mathbf{n})| \leqslant \Phi (\boldsymbol 0)$
for all
![]() $\mathbf{n} \in \mathbb Z^{k}$
, but it would be desirable to have a stronger inequality and ideally one that exhibits a power saving over the trivial bound. In the special case when
$\mathbf{n} \in \mathbb Z^{k}$
, but it would be desirable to have a stronger inequality and ideally one that exhibits a power saving over the trivial bound. In the special case when
![]() ${\mathfrak c}$
is the indicator function on a set
${\mathfrak c}$
is the indicator function on a set
![]() ${\mathcal X} \subseteq \mathbb Z \cap [-X,X]$
, the results of Theorems 1.1 and 3.1 achieve such a power saving for a large selection of
${\mathcal X} \subseteq \mathbb Z \cap [-X,X]$
, the results of Theorems 1.1 and 3.1 achieve such a power saving for a large selection of
![]() $\mathbf{n}$
and for all
$\mathbf{n}$
and for all
![]() $s \in \mathbb N$
below the critical point. In fact, it seems plausible that a careful modification of our arguments should apply also to a setting where the sequence
$s \in \mathbb N$
below the critical point. In fact, it seems plausible that a careful modification of our arguments should apply also to a setting where the sequence
![]() $({\mathfrak c}_{x})_{x \in \mathbb Z}$
takes nonnegative real values. However, it is less obvious how the proof of Lemma 2.1 would carry over to the general situation in which the weights
$({\mathfrak c}_{x})_{x \in \mathbb Z}$
takes nonnegative real values. However, it is less obvious how the proof of Lemma 2.1 would carry over to the general situation in which the weights
![]() ${\mathfrak c}$
may take complex values.
${\mathfrak c}$
may take complex values.
Finally, we remark that the saving of
![]() $X^{1/2}$
in Theorem 1.1 is optimal within the methods. This can be seen by noting that the shifting and averaging operation creates one dummy variable, on which we can expect no more than square-root cancellation. The analytically inclined reader may also be interested to note that the results of [Reference Bourgain, Demeter and Guth2, Reference Wooley11] require the underlying curve to have torsion and this is what enables the strong bounds on mean values of the exponential sum
$X^{1/2}$
in Theorem 1.1 is optimal within the methods. This can be seen by noting that the shifting and averaging operation creates one dummy variable, on which we can expect no more than square-root cancellation. The analytically inclined reader may also be interested to note that the results of [Reference Bourgain, Demeter and Guth2, Reference Wooley11] require the underlying curve to have torsion and this is what enables the strong bounds on mean values of the exponential sum
![]() $f_{k}({\boldsymbol \alpha };X)$
. The curve underlying the exponential sum
$f_{k}({\boldsymbol \alpha };X)$
. The curve underlying the exponential sum
![]() $g_{k}({\boldsymbol \alpha };X)$
, given by
$g_{k}({\boldsymbol \alpha };X)$
, given by
![]() $(p_{1}(t), \ldots , p_{k}(t))$
, does not have torsion over
$(p_{1}(t), \ldots , p_{k}(t))$
, does not have torsion over
![]() $\mathbb R^{k}$
, but it can be restricted to a
$\mathbb R^{k}$
, but it can be restricted to a
![]() $(k-\ell )$
-dimensional subspace in which it has torsion. This gives a geometric explanation for why our results are weaker as
$(k-\ell )$
-dimensional subspace in which it has torsion. This gives a geometric explanation for why our results are weaker as
![]() $\ell $
increases, and fail to give any improvement at all when
$\ell $
increases, and fail to give any improvement at all when
![]() $\ell $
is equal to k.
$\ell $
is equal to k.
Acknowledgement
The authors are grateful to Igor Shparlinski for useful discussions surrounding the topic of this paper.