Hostname: page-component-77c89778f8-9q27g Total loading time: 0 Render date: 2024-07-19T18:15:09.418Z Has data issue: false hasContentIssue false
  • English
  • Français

On the distribution of angles of the Salié sums

Published online by Cambridge University Press:  17 April 2009

Igor E. Shparlinski
Igor E. Shparlinski
Affiliation:
Department of Computing, Macquarie University, Sydney, NSW 2109, Australia, e-mail: igor@ics.mq.edu.au
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

For a prime p and integers a and b, we consider Salié sums

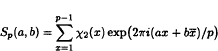
where χ2(x) is a quadratic character and x¯ is the modular inversion of x, that is, xx¯≡ 1 (mod p). One can naturally associate with Sp (a, b) a certain angle θp(a, b) ∈ [0, π]. We show that, for any fixed ε > 0, these angles are uniformly distributed in [0, π] when a and b run over arbitrary sets , ℬ ⊆ {0, 1, …, p − 1} such that there are at least p1+ε quadratic residues modulo p among the products ab, where (a, b) ∈  × ℬ.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 75 , Issue 2 , April 2007 , pp. 221 - 227
Copyright
Copyright © Australian Mathematical Society 2007

References

[1]Adolphson, A., ‘On the distribution of angles of Kloosterman sums’, J. Reine Angew. Math. 395 (1989), 214–220.Google Scholar
[2]Banks, W.D., Garaev, M.Z. and Shparlinski, I.E., ‘Density of non-residues in short intervals’, (preprint 2006).Google Scholar
[3]Chai, C.-L. and Li, W.-C.W., ‘Character sums, automorphic forms, equidistribution, and Ramanujan graphs. I: The Kloosterman sum conjecture over function fields’, Forum Math. 15 (2003), 679–699.CrossRefGoogle Scholar
[4]Duke, W., Priedlander, J.B. and Iwaniec, H., ‘Equidistribution of roots of a quadratic congruence to prime moduli’, Ann. of Math. 141 (1995), 423–441.CrossRefGoogle Scholar
[5]Fouvry, É. and Michel, P., ‘Sommes de modules de sommes d'exponentielles’, Pacific J. Math. 209 (2003), 261–288.CrossRefGoogle Scholar
[6]Fouvry, É. and Michel, P., ‘Sur le changement de signe des sommes de Kloosterman’, Ann. Math. (to appear).Google Scholar
[7]Iwaniec, H. and Kowalski, E., Analytic number theory (American Mathematical Society, Providence, RI, 2004).Google Scholar
[8]Katz, N.M., Gauss sums, Kloosterman sums, and monodromy groups (Princeton Univ. Press, Princeton, NJ, 1988).CrossRefGoogle Scholar
[9]Katz, N.M. and Sarnak, P., Random matrices, Frobenius eigenvalues, and monodromy (Amer. Math. Soc, Providence, RI, 1999).Google Scholar
[10]Laumon, G., ‘Exponential sums and l-adic cohomology: A survey’, Israel J. Math. 120 (2000), 225–257.CrossRefGoogle Scholar
[11]Lidl, R. and Niederreiter, H., Finite fields (Cambridge University Press, Cambridge, 1997).Google Scholar
[12]Michel, P., ‘Autour de la conjecture de Sato-Tate pour les sommes de Kloosterman, II’, Duke Math. J. 92 (1998), 221–254.CrossRefGoogle Scholar
[13]Michel, P., ‘Minoration de sommes d'exponentielles’, Duke Math. J. 95 (1998), 227–240.CrossRefGoogle Scholar
[14]Niederreiter, H., ‘The distribution of values of Kloosterman sums’, Arch. Math. 56 (1991), 270–277.CrossRefGoogle Scholar
[15]Sarnak, P., Some applications of modular forms (Cambridge University Press, Cambridge, 1990).CrossRefGoogle Scholar
[16]Shparlinski, I.E., ‘On the distribution of Kloosterman sums’, Proc. Amer. Math. Soc. (to appear).Google Scholar
[17]Tóth, Á., ‘Roots of quadratic congruences’, Internat. Math. Res. Notices 2000 (2000), 719–739.Google Scholar