Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Shehu, Yekini
2018.
Convergence Rate Analysis of Inertial Krasnoselskii–Mann Type Iteration with Applications.
Numerical Functional Analysis and Optimization,
Vol. 39,
Issue. 10,
p.
1077.
Matsushita, Shin-ya
2018.
A convergence rate of the proximal point algorithm in Banach spaces.
Optimization,
Vol. 67,
Issue. 6,
p.
881.
Suantai, Suthep
Witthayarat, Uamporn
Shehu, Yekini
and
Cholamjiak, Prasit
2019.
Iterative methods for the split feasibility problem and the fixed point problem in Banach spaces.
Optimization,
Vol. 68,
Issue. 5,
p.
955.
Sahu, D. R.
2020.
Applications of accelerated computational methods for quasi-nonexpansive operators to optimization problems.
Soft Computing,
Vol. 24,
Issue. 23,
p.
17887.
Li, Xiuxian
Meng, Min
and
Xie, Lihua
2020.
A Linearly Convergent Algorithm for Multi-Agent Quasi-Nonexpansive Operators in Real Hilbert Spaces.
p.
4903.
Li, Xiuxian
and
Xie, Lihua
2020.
Distributed algorithms for computing a fixed point of multi-agent nonexpansive operators.
Automatica,
Vol. 122,
Issue. ,
p.
109286.
Mukaidani, Hiroaki
Saravanakumar, Ramasamy
and
Xu, Hua
2020.
Robust incentive Stackelberg strategy for Markov jump linear stochastic systems via static output feedback.
IET Control Theory & Applications,
Vol. 14,
Issue. 9,
p.
1246.
Iyiola, Olaniyi S.
and
Shehu, Yekini
2021.
New Convergence Results for Inertial Krasnoselskii–Mann Iterations in Hilbert Spaces with Applications.
Results in Mathematics,
Vol. 76,
Issue. 2,
Dong, Yunda
2021.
Weak convergence of an extended splitting method for monotone inclusions.
Journal of Global Optimization,
Vol. 79,
Issue. 1,
p.
257.
Kimura, Yasunori
and
Nakagawa, Koichi
2021.
On the convergence rate of Mann iteration in geodesic spaces with positive curvature.
Optimization,
Vol. 70,
Issue. 5-6,
p.
929.
He, Songnian
Dong, Qiao-Li
Tian, Hanlin
and
Li, Xiao-Huan
2021.
On the optimal relaxation parameters of Krasnosel'ski–Mann iteration.
Optimization,
Vol. 70,
Issue. 9,
p.
1959.
Dong, Yunda
2021.
New inertial factors of the Krasnosel’skiı̆-Mann iteration.
Set-Valued and Variational Analysis,
Vol. 29,
Issue. 1,
p.
145.
Mukaidani, Hiroaki
Xu, Hua
and
Zhuang, Weihua
2021.
Robust static output feedback Nash strategy for uncertain Markov jump linear stochastic systems.
IET Control Theory & Applications,
Vol. 15,
Issue. 11,
p.
1559.
Li, Xiuxian
and
Feng, Gang
2021.
Distributed Algorithms for Computing a Common Fixed Point of a Group of Nonexpansive Operators.
IEEE Transactions on Automatic Control,
Vol. 66,
Issue. 5,
p.
2130.
Iyiola, Olaniyi S.
Enyi, Cyril D.
and
Shehu, Yekini
2022.
Reflected three-operator splitting method for monotone inclusion problem.
Optimization Methods and Software,
Vol. 37,
Issue. 4,
p.
1527.
Matsushita, Shin-ya
2022.
A splitting method for finding the resolvent of the sum of two maximal monotone operators.
Optimization,
Vol. 71,
Issue. 7,
p.
1863.
Dong, Yunda
and
Sun, Mengdi
2022.
New Acceleration Factors of the Krasnosel’skiĭ-Mann Iteration.
Results in Mathematics,
Vol. 77,
Issue. 5,
Dong, Qiao-Li
Cho, Yeol Je
He, Songnian
Pardalos, Panos M.
and
Rassias, Themistocles M.
2022.
The Krasnosel'skiĭ-Mann Iterative Method.
p.
29.
Shaho Alaviani, Seyyed
and
Kelkar, Atul G.
2023.
Generalized Semistability and Stochastic Semistability for Switched Nonlinear Systems Using Fixed Point Theory.
ASME Letters in Dynamic Systems and Control,
Vol. 3,
Issue. 3,
Boţ, Radu Ioan
and
Nguyen, Dang-Khoa
2023.
Fast Krasnosel’skiĭ–Mann Algorithm with a Convergence Rate of the Fixed Point Iteration of \(\boldsymbol{{ o} \left(\frac{1}{{ k}} \right)}\).
SIAM Journal on Numerical Analysis,
Vol. 61,
Issue. 6,
p.
2813.
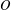 $O$ rate to little-
$O$ rate to little- $o$ without any other restrictions. The proof relies on the connection between the KM iteration and a useful technique on the convergence rate of summable sequences. Then we apply the result to give new results on convergence rates for the proximal point algorithm and the Douglas–Rachford method.
$o$ without any other restrictions. The proof relies on the connection between the KM iteration and a useful technique on the convergence rate of summable sequences. Then we apply the result to give new results on convergence rates for the proximal point algorithm and the Douglas–Rachford method.



