No CrossRef data available.
Article contents
A NOTE ON THE SUM OF RECIPROCALS
Published online by Cambridge University Press: 17 May 2019
Abstract
We prove that, given a positive integer 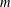 $m$, there is a sequence
$m$, there is a sequence 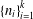 $\{n_{i}\}_{i=1}^{k}$ of positive integers such that
$\{n_{i}\}_{i=1}^{k}$ of positive integers such that 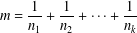 $$\begin{eqnarray}m=\frac{1}{n_{1}}+\frac{1}{n_{2}}+\cdots +\frac{1}{n_{k}}\end{eqnarray}$$
$$\begin{eqnarray}m=\frac{1}{n_{1}}+\frac{1}{n_{2}}+\cdots +\frac{1}{n_{k}}\end{eqnarray}$$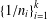 $\{1/n_{i}\}_{i=1}^{k}$ do not represent other integers.
$\{1/n_{i}\}_{i=1}^{k}$ do not represent other integers.
- Type
- Research Article
- Information
- Bulletin of the Australian Mathematical Society , Volume 100 , Issue 2 , October 2019 , pp. 189 - 193
- Copyright
- © 2019 Australian Mathematical Publishing Association Inc.




