Article contents
A NOTE ON THE DIOPHANTINE EQUATION 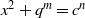 ${x}^{2} + {q}^{m} = {c}^{n} $
${x}^{2} + {q}^{m} = {c}^{n} $
Published online by Cambridge University Press: 26 November 2013
Abstract
Let 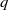 $q$ be an odd prime such that
$q$ be an odd prime such that 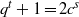 ${q}^{t} + 1= 2{c}^{s} $, where
${q}^{t} + 1= 2{c}^{s} $, where 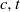 $c, t$ are positive integers and
$c, t$ are positive integers and 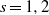 $s= 1, 2$. We show that the Diophantine equation
$s= 1, 2$. We show that the Diophantine equation 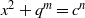 ${x}^{2} + {q}^{m} = {c}^{n} $ has only the positive integer solution
${x}^{2} + {q}^{m} = {c}^{n} $ has only the positive integer solution 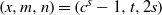 $(x, m, n)= ({c}^{s} - 1, t, 2s)$ under some conditions. The proof is based on elementary methods and a result concerning the Diophantine equation
$(x, m, n)= ({c}^{s} - 1, t, 2s)$ under some conditions. The proof is based on elementary methods and a result concerning the Diophantine equation 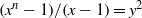 $({x}^{n} - 1)/ (x- 1)= {y}^{2} $ due to Ljunggren. We also verify that when
$({x}^{n} - 1)/ (x- 1)= {y}^{2} $ due to Ljunggren. We also verify that when 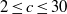 $2\leq c\leq 30$ with
$2\leq c\leq 30$ with 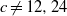 $c\not = 12, 24$, the Diophantine equation
$c\not = 12, 24$, the Diophantine equation 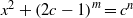 ${x}^{2} + \mathop{(2c- 1)}\nolimits ^{m} = {c}^{n} $ has only the positive integer solution
${x}^{2} + \mathop{(2c- 1)}\nolimits ^{m} = {c}^{n} $ has only the positive integer solution 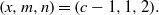 $(x, m, n)= (c- 1, 1, 2). $
$(x, m, n)= (c- 1, 1, 2). $
Keywords
MSC classification
- Type
- Research Article
- Information
- Copyright
- Copyright ©2013 Australian Mathematical Publishing Association Inc.
References
- 9
- Cited by




