Hostname: page-component-8448b6f56d-jr42d Total loading time: 0 Render date: 2024-04-25T00:41:33.637Z Has data issue: false hasContentIssue false
  • English
  • Français

A NILPOTENCY CRITERION FOR SOME VERBAL SUBGROUPS

Part of: Special aspects of infinite or finite groups

Published online by Cambridge University Press:  27 February 2019

CARMINE MONETTA Open the ORCID record for CARMINE MONETTA [Opens in a new window]  and
ANTONIO TORTORA Open the ORCID record for ANTONIO TORTORA [Opens in a new window]
CARMINE MONETTA*
Affiliation:
Dipartimento di Matematica, Università di Salerno, Via Giovanni Paolo II, 132, 84084 Fisciano (SA), Italy email cmonetta@unisa.it
ANTONIO TORTORA
Affiliation:
Dipartimento di Matematica, Università di Salerno, Via Giovanni Paolo II, 132, 84084 Fisciano (SA), Italy Dipartimento di Matematica e Fisica, Università della Campania ‘Luigi Vanvitelli’ Viale Lincoln, 5, 81100 Caserta (CE), Italy email antortora@unisa.it, antonio.tortora@unicampania.it
*
✉cmonetta@unisa.it
Get access Rights & Permissions [Opens in a new window]

Abstract

The word 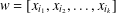$w=[x_{i_{1}},x_{i_{2}},\ldots ,x_{i_{k}}]$ is a simple commutator word if 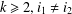$k\geq 2,i_{1}\neq i_{2}$ and 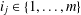$i_{j}\in \{1,\ldots ,m\}$ for some 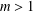$m>1$. For a finite group 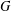$G$, we prove that if 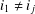$i_{1}\neq i_{j}$ for every 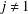$j\neq 1$, then the verbal subgroup corresponding to 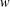$w$ is nilpotent if and only if 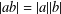$|ab|=|a||b|$ for any $w$-values $a,b\in G$ of coprime orders. We also extend the result to a residually finite group 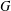$G$, provided that the set of all 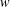$w$-values in 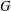$G$ is finite.

Keywords

nilpotentEngel wordverbal subgroup

MSC classification

Primary: 20F18: Nilpotent groups
Secondary: 20F45: Engel conditions
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 100 , Issue 2 , October 2019 , pp. 281 - 289
Copyright
© 2019 Australian Mathematical Publishing Association Inc. 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The authors are members of National Group for Algebraic and Geometric Structures and their Applications (GNSAGA–INdAM).

References

Bastos, R., Monetta, C. and Shumyatsky, P., ‘A criterion for metanilpotency of a finite group’, J. Group Theory 21(4) (2018), 713–718.10.1515/jgth-2018-0002Google Scholar
Bastos, R. and Shumyatsky, P., ‘A sufficient condition for nilpotency of the commutator subgroup’, Sib. Math. J. 57(5) (2016), 762–763.Google Scholar
Baumslag, B. and Wiegold, J., ‘A sufficient condition for nilpotency in a finite group’, Preprint, 2014, arXiv:1411.2877 [math.GR].Google Scholar
Bloom, D. M., ‘The subgroups of PSL(3, q) for odd q ’, Trans. Amer. Math. Soc. 127 (1967), 150–178.Google Scholar
Detomi, E., Morigi, M. and Shumyatsky, P., ‘Words of Engel type are concise in residually finite groups’, Bull. Math. Sci. (2018), to appear.10.1142/S1664360719500127Google Scholar
Gorenstein, D., Finite Groups, 2nd edn (Chelsea, New York, 1980).Google Scholar
Huppert, B., Endliche Gruppen I (Springer, Berlin–New York, 1967).Google Scholar
Isaacs, I. M., Finite Group Theory, Graduate Studies in Mathematics, 92 (American Mathematical Society, Providence, RI, 2008).Google Scholar
Kassabov, M. and Nikolov, N., ‘Words with few values in finite simple groups’, Q. J. Math. 64(4) (2013), 1161–1166.10.1093/qmath/has018Google Scholar
Robinson, D. J. S., Finiteness Conditions and Generalized Soluble Groups, Parts 1 and 2 (Springer, Berlin, 1972).10.1007/978-3-662-11747-7Google Scholar
Suzuki, M., ‘On a class of doubly transitive groups’, Ann. of Math. (2) 75 (1962), 105–145.Google Scholar
Suzuki, M., Group Theory I (Springer, Berlin–New York, 1982).10.1007/978-3-642-61804-8Google Scholar
Thompson, J. G., ‘Nonsolvable finite groups all of whose local subgroups are solvable’, Bull. Amer. Math. Soc. 74 (1968), 383–437.10.1090/S0002-9904-1968-11953-6Google Scholar
Turull, A., ‘Fitting height of groups and of fixed points’, J. Algebra 86(2) (1984), 555–566.10.1016/0021-8693(84)90048-6Google Scholar