Hostname: page-component-76fb5796d-9pm4c Total loading time: 0 Render date: 2024-04-27T01:20:28.243Z Has data issue: false hasContentIssue false
  • English
  • Français

Mazur's intersection property of balls for compact convex sets

Published online by Cambridge University Press:  17 April 2009

J. H. M. Whitfield  and
V. Zizler
J. H. M. Whitfield
Affiliation:
Department of Mathematical Sciences, Lakehead University, Thunder Bay, Ontario, Canada P7B 5E1
V. Zizler
Affiliation:
Department of Mathematics, University of Alberta, Edmonton, Alberta, Canada T6G 2G1
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We show that every compact convex set in a Banach space X is an intersection of balls provided the cone generated by the set of all extreme points of the dual unit ball 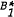of X* is dense in X* in the topology of uniform convergence on compact sets in X. This allows us to renorm every Banach space with transfinite Schauder basis by a norm which shares the mentioned intersection property.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 35 , Issue 2 , April 1987 , pp. 267 - 274
Copyright
Copyright © Australian Mathematical Society 1987

References

[1]Bessaga, C. and Pelczynski, A., Selected topics in infinite dimensional topology, Polish Sci. Publ. Warsaw 1975.Google Scholar
[2]Choquet, G., Lectures on Analysis, Vol. II, Representation Theory, Edited by Marsden, J., W.A. Benjamin, Inc. 1969.Google Scholar
[3]Giles, J.R., Gregory, D.A. and Sims, Brailey, “Characterization of normed linear spaces with Mazur's intersection property”, Bull. Austral. Math. Soc. 18 (1978), 105–123.CrossRefGoogle Scholar
[4]Mazur, S., “Uber Schwach Konvergenz in der Raumen (Lp)”, Studia. Math. 4 (1933), 128–133.CrossRefGoogle Scholar
[5]Phelps, R.R., “A representation theorem for bounded convex sets”, Proc. Amer. Math. Soc. 11 (1960), 976–983.CrossRefGoogle Scholar
[6]Rainwater, John, “Local uniform convexity of Day's norm on c0 (Γ)”, Proc. Amer. Math. Soc. 22 (1969), 335–339.Google Scholar
[7]Rainwater, John, “Day's norm on c0 (Γ)”, Various Publ. Ser. No. 8. (1969).Google Scholar
[8]Sullivan, F., “Dentability, “Smoothability and stronger properties in Banach spaces”, Indiana Math. J. 26 (1977), 545–553.CrossRefGoogle Scholar