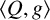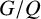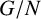1 Introduction
A classical theorem of Schur [Reference Schur14] states that if the centre
![]() $\zeta (G)$
of a group G has finite index, then the commutator subgroup
$\zeta (G)$
of a group G has finite index, then the commutator subgroup
![]() $G'$
is finite. Several results of Schur type were later proved by replacing the finiteness of the index
$G'$
is finite. Several results of Schur type were later proved by replacing the finiteness of the index
![]() $|G:\zeta (G)|$
with a suitable restriction on the factor group
$|G:\zeta (G)|$
with a suitable restriction on the factor group
![]() $G/\zeta (G)$
. It is known for instance that if G is a group such that
$G/\zeta (G)$
. It is known for instance that if G is a group such that
![]() $G/\zeta (G)$
is Černikov, then also
$G/\zeta (G)$
is Černikov, then also
![]() $G'$
is a Černikov group, that is, an abelian-by-finite group satisfying the minimal condition on subgroups. This latter result has been often, and erroneously, attributed to Polovickiı̆ (see for instance [Reference Franciosi, de Giovanni and Kurdachenko6, Reference Otal8] and [Reference Robinson10, Part 1, Theorem 4.23]); actually, it was due to Černikov [Reference Černikov1], and Polovickiı̆ himself wrote in [Reference Polovickiĭ9]: ‘This proposition is easily obtained from our Lemma 1, in view of the result proved in [Reference Černikov1] which states the extremality of the commutator subgroup of any central extension by an extremal group’. A proof of Černikov’s theorem can also be found in a paper of Schlette [Reference Schlette12], where she also proved that if G is a group such that
$G'$
is a Černikov group, that is, an abelian-by-finite group satisfying the minimal condition on subgroups. This latter result has been often, and erroneously, attributed to Polovickiı̆ (see for instance [Reference Franciosi, de Giovanni and Kurdachenko6, Reference Otal8] and [Reference Robinson10, Part 1, Theorem 4.23]); actually, it was due to Černikov [Reference Černikov1], and Polovickiı̆ himself wrote in [Reference Polovickiĭ9]: ‘This proposition is easily obtained from our Lemma 1, in view of the result proved in [Reference Černikov1] which states the extremality of the commutator subgroup of any central extension by an extremal group’. A proof of Černikov’s theorem can also be found in a paper of Schlette [Reference Schlette12], where she also proved that if G is a group such that
![]() $G/\zeta (G)$
is Černikov, then G is abelian-by-finite.
$G/\zeta (G)$
is Černikov, then G is abelian-by-finite.
A different approach to Schur’s theorem was adopted in [Reference De Falco, de Giovanni and Musella2] by replacing the centre by a normal subgroup with a suitable embedding property. Obviously, a subgroup C of a group G is contained in
![]() $\zeta (G)$
if and only if
$\zeta (G)$
if and only if
![]() $\langle g,C\rangle $
is abelian for all
$\langle g,C\rangle $
is abelian for all
![]() $g\in G$
, and we say that a subgroup Q is permutably embedded in G if
$g\in G$
, and we say that a subgroup Q is permutably embedded in G if
![]() $\langle g,Q\rangle $
is quasihamiltonian for all
$\langle g,Q\rangle $
is quasihamiltonian for all
![]() $g\in G$
; here a group is called quasihamiltonian if
$g\in G$
; here a group is called quasihamiltonian if
![]() $XY=YX$
for all its subgroups X and Y. It was proved in [Reference De Falco, de Giovanni and Musella2] that if a group G contains a permutably embedded subgroup of finite index, then there exists a finite normal subgroup N of G such that the factor group
$XY=YX$
for all its subgroups X and Y. It was proved in [Reference De Falco, de Giovanni and Musella2] that if a group G contains a permutably embedded subgroup of finite index, then there exists a finite normal subgroup N of G such that the factor group
![]() $G/N$
is quasihamiltonian.
$G/N$
is quasihamiltonian.
The aim of this paper is to look at groups which are Černikov over a permutably embedded normal subgroup and so our first main result should be compared with the above quoted theorem of Schlette; recall here that a group is Černikov if and only if it contains a subgroup of finite index which is the direct product of finitely many Prüfer subgroups.
Theorem 1.1. Let G be a group containing a permutably embedded normal subgroup Q such that
![]() $G/Q$
is a Černikov group and let
$G/Q$
is a Černikov group and let
![]() $J/Q$
be the largest divisible subgroup of
$J/Q$
be the largest divisible subgroup of
![]() $G/Q$
. Then J is quasihamiltonian and, in particular, G is quasihamiltonian-by-finite.
$G/Q$
. Then J is quasihamiltonian and, in particular, G is quasihamiltonian-by-finite.
Our second main result shows that in the periodic case, a satisfactory translation of Černikov’s theorem in terms of permutability holds.
Theorem 1.2. Let G be a periodic group containing a permutably embedded normal subgroup Q such that
![]() $G/Q$
is a Černikov group. Then G has a Černikov normal subgroup N such that
$G/Q$
is a Černikov group. Then G has a Černikov normal subgroup N such that
![]() $G/N$
is quasihamiltonian.
$G/N$
is quasihamiltonian.
Our notation is mostly standard and can be found in [Reference Robinson10].
2 Preliminaries
A modular lattice
![]() $\mathfrak {L }$
is called permodular if for all elements a and b of
$\mathfrak {L }$
is called permodular if for all elements a and b of
![]() $\mathfrak {L}$
such that
$\mathfrak {L}$
such that
![]() $b\leq a$
, the interval
$b\leq a$
, the interval
![]() $[a/b]=\{ x\in \mathfrak {L}\;|\; b\leq x\leq a\}$
is finite whenever it has finite length. Moreover, if G is a group and
$[a/b]=\{ x\in \mathfrak {L}\;|\; b\leq x\leq a\}$
is finite whenever it has finite length. Moreover, if G is a group and
![]() $\mathfrak {L}(G)$
is the lattice of all subgroups of G, a modular element M of
$\mathfrak {L}(G)$
is the lattice of all subgroups of G, a modular element M of
![]() $\mathfrak {L}(G)$
is said to be permodular in G if the index
$\mathfrak {L}(G)$
is said to be permodular in G if the index
![]() $|\langle M,g\rangle :Y|$
is finite for all elements g and for all subgroups Y of G such that
$|\langle M,g\rangle :Y|$
is finite for all elements g and for all subgroups Y of G such that
![]() $M\leq Y\leq \langle M,g\rangle $
and the interval
$M\leq Y\leq \langle M,g\rangle $
and the interval
![]() $[\langle M,g\rangle /Y]$
is finite. Since cyclic subgroups and subgroups of finite index can be detected within the lattice of subgroups, permodular subgroups are recognisable by means of purely lattice theoretic concepts. Actually, it is known that a group has a permodular subgroup lattice if and only if all its subgroups are permodular (see [Reference Schmidt13, Theorem 6.4.3]). Notice here that every finite modular lattice is obviously permodular, but, for instance, the subgroup lattice of a Tarski group (that is, an infinite simple group whose proper nontrivial subgroups have prime order) is modular but not permodular.
$[\langle M,g\rangle /Y]$
is finite. Since cyclic subgroups and subgroups of finite index can be detected within the lattice of subgroups, permodular subgroups are recognisable by means of purely lattice theoretic concepts. Actually, it is known that a group has a permodular subgroup lattice if and only if all its subgroups are permodular (see [Reference Schmidt13, Theorem 6.4.3]). Notice here that every finite modular lattice is obviously permodular, but, for instance, the subgroup lattice of a Tarski group (that is, an infinite simple group whose proper nontrivial subgroups have prime order) is modular but not permodular.
Recall also that a subgroup X of a group G is said to be permutable in G if
![]() $XY=YX$
for all subgroups Y of G. Thus, a group is quasihamiltonian if and only if all its subgroups are permutable. Since a subgroup is permutable if and only if it is modular and ascendant (see for instance [Reference Schmidt13, Theorem 6.2.10]), it follows that a group is quasihamiltonian if and only if it is locally nilpotent and its subgroup lattice is modular. Thus, the study of periodic quasihamiltonian groups reduces to that of primary quasihamiltonian groups, and these latter are known to be either abelian or nilpotent of finite exponent (see [Reference Schmidt13, Theorem 2.4.14]). The structure of nonperiodic quasihamiltonian groups is described by the following result (see [Reference Schmidt13, Theorem 2.4.11]); it shows in particular that the commutator subgroup of any quasihamiltonian group is locally finite.
$XY=YX$
for all subgroups Y of G. Thus, a group is quasihamiltonian if and only if all its subgroups are permutable. Since a subgroup is permutable if and only if it is modular and ascendant (see for instance [Reference Schmidt13, Theorem 6.2.10]), it follows that a group is quasihamiltonian if and only if it is locally nilpotent and its subgroup lattice is modular. Thus, the study of periodic quasihamiltonian groups reduces to that of primary quasihamiltonian groups, and these latter are known to be either abelian or nilpotent of finite exponent (see [Reference Schmidt13, Theorem 2.4.14]). The structure of nonperiodic quasihamiltonian groups is described by the following result (see [Reference Schmidt13, Theorem 2.4.11]); it shows in particular that the commutator subgroup of any quasihamiltonian group is locally finite.
Lemma 2.1. Let G be a quasihamiltonian group which is neither periodic nor abelian. Then the subgroup T of all elements of finite order of G is abelian and the torsion-free group
![]() $G/T$
is locally cyclic. Moreover, all subgroups of T are normal in G and each element of G whose order is either a prime or
$G/T$
is locally cyclic. Moreover, all subgroups of T are normal in G and each element of G whose order is either a prime or
![]() $4$
belongs to
$4$
belongs to
![]() $\zeta (G)$
.
$\zeta (G)$
.
We refer to the monograph [Reference Schmidt13, Chs. 5 and 6] for further results concerning the behaviour of permutable and permodular subgroups of infinite groups that can be useful for our considerations. We only note here that if Q is a permutably embedded subgroup of a group G, then Q is permutable in G and quasihamiltonian.
3 Proof of Theorem 1.1
Let G be a group and let X be a subgroup of G. We say that the interval
![]() $[G/X]$
of
$[G/X]$
of
![]() $\mathfrak {L}(G)$
is Černikov if it satisfies the minimal condition and there exists a permodular subgroup P of G containing X such that the index
$\mathfrak {L}(G)$
is Černikov if it satisfies the minimal condition and there exists a permodular subgroup P of G containing X such that the index
![]() $|G:P|$
is finite and the lattice
$|G:P|$
is finite and the lattice
![]() $[P/X]$
is permodular. Since periodic groups with a permodular subgroup lattice are locally finite (see [Reference Schmidt13, Theorem 2.4.16]) and locally finite groups satisfying the minimal condition are Černikov groups by an important theorem of Šunkov (see for instance [Reference Dixon4, Theorem 1.6.15]), a group G is Černikov if and only if
$[P/X]$
is permodular. Since periodic groups with a permodular subgroup lattice are locally finite (see [Reference Schmidt13, Theorem 2.4.16]) and locally finite groups satisfying the minimal condition are Černikov groups by an important theorem of Šunkov (see for instance [Reference Dixon4, Theorem 1.6.15]), a group G is Černikov if and only if
![]() $\mathfrak {L}(G)=[G/\{1\}]$
is a Černikov lattice.
$\mathfrak {L}(G)=[G/\{1\}]$
is a Černikov lattice.
It is well known that a group is locally cyclic if and only if it has a distributive subgroup lattice (see [Reference Schmidt13, Theorem 1.2.3]), and so our first lemma may be considered as a translation of the elementary fact that a group G is abelian when the factor group
![]() $G/\zeta (G)$
is locally cyclic.
$G/\zeta (G)$
is locally cyclic.
Lemma 3.1. Let G be a group containing a permutably embedded subgroup Q such that the interval
![]() $[G/Q]$
is a distributive lattice. Then G is quasihamiltonian.
$[G/Q]$
is a distributive lattice. Then G is quasihamiltonian.
Proof. Let E be any finitely generated subgroup of G. Then
is a distributive lattice, and so, in particular, the finitely generated group
![]() $E/(E\cap Q)^E$
is cyclic. Moreover, the index
$E/(E\cap Q)^E$
is cyclic. Moreover, the index
![]() $|(E\cap Q)^E:E\cap Q|$
is finite because
$|(E\cap Q)^E:E\cap Q|$
is finite because
![]() $E\cap Q$
is permutable in G (see [Reference Schmidt13, Lemma 6.2.8]). Thus, the lattice
$E\cap Q$
is permutable in G (see [Reference Schmidt13, Lemma 6.2.8]). Thus, the lattice
![]() $[E/E\cap Q]$
satisfies the maximal condition so that there exists an element x such that
$[E/E\cap Q]$
satisfies the maximal condition so that there exists an element x such that
![]() $E=\langle x,E\cap Q\rangle $
(see [Reference De Falco, de Giovanni and Musella3, Corollary 2.4]) and hence E is quasihamiltonian. Since the property of being quasihamiltonian is local, it follows that G is also a quasihamiltonian group.
$E=\langle x,E\cap Q\rangle $
(see [Reference De Falco, de Giovanni and Musella3, Corollary 2.4]) and hence E is quasihamiltonian. Since the property of being quasihamiltonian is local, it follows that G is also a quasihamiltonian group.
Lemma 3.2. Let G be a group and let N be a periodic normal subgroup of G. If N is contained in the hypercentre of G and
![]() $G/C_G(N)$
has no proper subgroups of finite index, then
$G/C_G(N)$
has no proper subgroups of finite index, then
![]() $N\leq \zeta (G)$
.
$N\leq \zeta (G)$
.
Proof. Assume for a contradiction that N is not contained in
![]() $\zeta (G)$
so that
$\zeta (G)$
so that
![]() $N\cap \zeta (G)$
is a proper subgroup of
$N\cap \zeta (G)$
is a proper subgroup of
![]() $N\cap \zeta _2(G)$
. Consider an element a of
$N\cap \zeta _2(G)$
. Consider an element a of
![]() $\bigl (N\cap \zeta _2(G)\bigr )\setminus \zeta (G)$
and let k be the order of a. Since the map
$\bigl (N\cap \zeta _2(G)\bigr )\setminus \zeta (G)$
and let k be the order of a. Since the map
![]() $g\mapsto [a,g]$
is an epimorphism from G onto
$g\mapsto [a,g]$
is an epimorphism from G onto
![]() $[a,G]$
with kernel
$[a,G]$
with kernel
![]() $C_G(a)$
, the nontrivial subgroup
$C_G(a)$
, the nontrivial subgroup
![]() $[a,G]$
is a homomorphic image of
$[a,G]$
is a homomorphic image of
![]() $G/C_G(N)$
, which is impossible because
$G/C_G(N)$
, which is impossible because
![]() $[a,G]^k=[a^k,G]=\{1\}$
.
$[a,G]^k=[a^k,G]=\{1\}$
.
Lemma 3.3. Let G be a group containing a permutably embedded nonperiodic subgroup Q such that the interval
![]() $[G/Q]$
is a Černikov lattice. Then the elements of finite order of G form a locally finite subgroup T containing
$[G/Q]$
is a Černikov lattice. Then the elements of finite order of G form a locally finite subgroup T containing
![]() $G'$
and
$G'$
and
![]() $Q\cap T\leq \zeta (T)$
. Moreover, all periodic subgroups of Q are normal in G and each element of Q whose order is either a prime or
$Q\cap T\leq \zeta (T)$
. Moreover, all periodic subgroups of Q are normal in G and each element of Q whose order is either a prime or
![]() $4$
belongs to
$4$
belongs to
![]() $\zeta (G)$
.
$\zeta (G)$
.
Proof. By Schlette’s result, we may suppose that Q is not contained in
![]() $\zeta (G)$
so that there is a
$\zeta (G)$
so that there is a
![]() $g\in G$
such that
$g\in G$
such that
![]() $[Q,g]\neq \{1\}$
. Since the subgroup
$[Q,g]\neq \{1\}$
. Since the subgroup
![]() $\langle g,Q\rangle $
is quasihamiltonian, it follows from Lemma 2.1 that Q has torsion-free rank
$\langle g,Q\rangle $
is quasihamiltonian, it follows from Lemma 2.1 that Q has torsion-free rank
![]() $1$
. Let E be any finitely generated subgroup of G and put
$1$
. Let E be any finitely generated subgroup of G and put
![]() $X=\langle Q,E\rangle $
and
$X=\langle Q,E\rangle $
and
![]() $Y=Q^X$
. Then
$Y=Q^X$
. Then
![]() $X/Y$
is finitely generated and
$X/Y$
is finitely generated and
![]() $\mathfrak {L}(X/Y)$
is a Černikov lattice so that
$\mathfrak {L}(X/Y)$
is a Černikov lattice so that
![]() $X/Y$
is finite. Moreover, the index
$X/Y$
is finite. Moreover, the index
![]() $|Y:Q|$
is finite (see [Reference Schmidt13, Lemma 6.2.8]) and hence Q has finite index in X. It follows now from [Reference De Falco, de Giovanni and Musella2, Theorem 3.5] that X contains a finite normal subgroup L such that
$|Y:Q|$
is finite (see [Reference Schmidt13, Lemma 6.2.8]) and hence Q has finite index in X. It follows now from [Reference De Falco, de Giovanni and Musella2, Theorem 3.5] that X contains a finite normal subgroup L such that
![]() $X/L$
is quasihamiltonian. Thus,
$X/L$
is quasihamiltonian. Thus,
![]() $X'$
is locally finite so the arbitrary choice of E yields that
$X'$
is locally finite so the arbitrary choice of E yields that
![]() $G'$
is locally finite and hence the elements of finite order of G form a locally finite subgroup T containing
$G'$
is locally finite and hence the elements of finite order of G form a locally finite subgroup T containing
![]() $G'$
. If x is any element of T, the nonperiodic subgroup
$G'$
. If x is any element of T, the nonperiodic subgroup
![]() $\langle x,Q\rangle $
is quasihamiltonian so that
$\langle x,Q\rangle $
is quasihamiltonian so that
![]() $\langle x,Q\cap T\rangle $
is abelian by Lemma 2.1 and hence
$\langle x,Q\cap T\rangle $
is abelian by Lemma 2.1 and hence
![]() $Q\cap T\leq \zeta (T)$
.
$Q\cap T\leq \zeta (T)$
.
Let a be any element of infinite order of G. Then
![]() $\langle a,Q\rangle $
is quasihamiltonian so that a normalises all subgroups of
$\langle a,Q\rangle $
is quasihamiltonian so that a normalises all subgroups of
![]() $Q\cap T$
and centralises each element of Q which has order either a prime or
$Q\cap T$
and centralises each element of Q which has order either a prime or
![]() $4$
(see [Reference Schmidt13, Theorem 2.4.11]). Since G is generated by its elements of infinite order, the proof is complete.
$4$
(see [Reference Schmidt13, Theorem 2.4.11]). Since G is generated by its elements of infinite order, the proof is complete.
Proof of Theorem 1.1
Since
![]() $G/Q$
is Černikov, the subgroup J has finite index in G and so it is enough to prove that J is quasihamiltonian. Thus without loss of generality, we may assume that
$G/Q$
is Černikov, the subgroup J has finite index in G and so it is enough to prove that J is quasihamiltonian. Thus without loss of generality, we may assume that
![]() $G/Q$
is a direct product of
$G/Q$
is a direct product of
![]() $r\geq 1$
Prüfer subgroups. Suppose first
$r\geq 1$
Prüfer subgroups. Suppose first
![]() $r=1$
so that
$r=1$
so that
![]() $G/Q$
is a group of type
$G/Q$
is a group of type
![]() $q^\infty $
for some prime number q and hence the subgroup lattice of
$q^\infty $
for some prime number q and hence the subgroup lattice of
![]() $G/Q$
is distributive. In this case, the group G is quasihamiltonian by Lemma 3.1. Assume now
$G/Q$
is distributive. In this case, the group G is quasihamiltonian by Lemma 3.1. Assume now
![]() $r>1$
. Let p be any prime in the set
$r>1$
. Let p be any prime in the set
![]() $\pi =\pi (G/Q)$
and
$\pi =\pi (G/Q)$
and
![]() $P/Q$
any subgroup of type
$P/Q$
any subgroup of type
![]() $p^\infty $
of
$p^\infty $
of
![]() $G/Q$
. Thus,
$G/Q$
. Thus,
where
![]() $V/Q$
is the direct product of
$V/Q$
is the direct product of
![]() $r-1$
Prüfer subgroups so that P is quasihamiltonian by the first part of the proof, while V is quasihamiltonian by induction on r. In particular, P and V are hypercentral and hence
$r-1$
Prüfer subgroups so that P is quasihamiltonian by the first part of the proof, while V is quasihamiltonian by induction on r. In particular, P and V are hypercentral and hence
![]() $G=PV$
is also a hypercentral group (see [Reference Robinson10, Part 1, page 51]).
$G=PV$
is also a hypercentral group (see [Reference Robinson10, Part 1, page 51]).
Suppose that G is periodic and write
![]() $P=P_1\times P_2$
, where
$P=P_1\times P_2$
, where
![]() $P_1$
is a p-subgroup and
$P_1$
is a p-subgroup and
![]() $P_2$
is a
$P_2$
is a
![]() $p'$
-subgroup. Since
$p'$
-subgroup. Since
![]() $P_1$
has infinite exponent, it is abelian (see [Reference Schmidt13, Theorem 2.4.14]) and so
$P_1$
has infinite exponent, it is abelian (see [Reference Schmidt13, Theorem 2.4.14]) and so
![]() $P_1\leq \zeta (P)$
. Thus,
$P_1\leq \zeta (P)$
. Thus,
![]() $Q\leq C_G(P_1)$
and hence
$Q\leq C_G(P_1)$
and hence
![]() $G/C_G(P_1)$
is divisible. Application of Lemma 3.2 yields that
$G/C_G(P_1)$
is divisible. Application of Lemma 3.2 yields that
![]() $P_1$
is contained in
$P_1$
is contained in
![]() $\zeta (G)$
. It follows that the largest
$\zeta (G)$
. It follows that the largest
![]() $\pi $
-subgroup
$\pi $
-subgroup
![]() $O_\pi (G)$
of G lies in
$O_\pi (G)$
of G lies in
![]() $\zeta (G)$
. However, the largest
$\zeta (G)$
. However, the largest
![]() $\pi '$
-subgroup
$\pi '$
-subgroup
![]() $O_{\pi '}(G)$
of G is contained in Q and hence
$O_{\pi '}(G)$
of G is contained in Q and hence
![]() $G=O_\pi (G)\times O_{\pi '}(G)$
is quasihamiltonian.
$G=O_\pi (G)\times O_{\pi '}(G)$
is quasihamiltonian.
Assume finally that G is not periodic so that Q is not periodic. It follows from Lemma 3.3 that
![]() $G'$
is locally finite, whence the elements of finite order of G form a locally finite subgroup T and
$G'$
is locally finite, whence the elements of finite order of G form a locally finite subgroup T and
![]() $G'\leq Q\cap T\leq \zeta (T)$
. Let x be any element of T and put
$G'\leq Q\cap T\leq \zeta (T)$
. Let x be any element of T and put
![]() $C=C_G(x)$
. Then
$C=C_G(x)$
. Then
![]() $G'\leq C$
and so C is normal in G. Since
$G'\leq C$
and so C is normal in G. Since
![]() $\langle x,Q\rangle $
is a nonperiodic quasihamiltonian group, the subgroup
$\langle x,Q\rangle $
is a nonperiodic quasihamiltonian group, the subgroup
![]() $\langle x\rangle $
is normalised by Q so that
$\langle x\rangle $
is normalised by Q so that
![]() $N_G(\langle x\rangle )$
is normal in G and
$N_G(\langle x\rangle )$
is normal in G and
![]() $G/N_G(\langle x\rangle )$
is a Černikov group. It follows that
$G/N_G(\langle x\rangle )$
is a Černikov group. It follows that
![]() $G/C$
is also Černikov. If
$G/C$
is also Černikov. If
![]() $R/C$
is the largest divisible subgroup of
$R/C$
is the largest divisible subgroup of
![]() $G/C$
, Lemma 3.2 yields that R centralises x and so x has only finitely many conjugates in G. Thus,
$G/C$
, Lemma 3.2 yields that R centralises x and so x has only finitely many conjugates in G. Thus,
![]() $G/C$
is finite so that
$G/C$
is finite so that
![]() $G=QC$
and
$G=QC$
and
![]() $\langle x\rangle $
is normal in G. Moreover, by Lemma 2.1,
$\langle x\rangle $
is normal in G. Moreover, by Lemma 2.1,
![]() $[x,Q]=\{1\}$
whenever the order of x is a prime or
$[x,Q]=\{1\}$
whenever the order of x is a prime or
![]() $4$
and so
$4$
and so
![]() $[x,G]=\{1\}$
under the same assumption. Therefore the group G is quasihamiltonian (see [Reference Schmidt13, Theorem 2.4.11]) and the proof is complete.
$[x,G]=\{1\}$
under the same assumption. Therefore the group G is quasihamiltonian (see [Reference Schmidt13, Theorem 2.4.11]) and the proof is complete.
4 Proof of Theorem 1.2
The first result of this section is an elementary lemma concerning divisible homomorphic images of abelian groups.
Lemma 4.1. Let A be an abelian group and let B be a subgroup of A of finite exponent e. If
![]() $A/B$
is divisible, then
$A/B$
is divisible, then
![]() $A^e$
is the largest divisible subgroup of A. Moreover, if
$A^e$
is the largest divisible subgroup of A. Moreover, if
![]() $A/B$
is a group of type
$A/B$
is a group of type
![]() $p^\infty $
for some prime number p, then
$p^\infty $
for some prime number p, then
![]() $A^e$
is also of type
$A^e$
is also of type
![]() $p^\infty $
.
$p^\infty $
.
Proof. The map
![]() $a\longmapsto a^e$
defines an epimorphism of A onto
$a\longmapsto a^e$
defines an epimorphism of A onto
![]() $A^e$
whose kernel contains B so that
$A^e$
whose kernel contains B so that
![]() $A^e$
is divisible and hence
$A^e$
is divisible and hence
![]() $A=A^e\times C$
for a suitable subgroup C. Obviously, C has finite exponent and so
$A=A^e\times C$
for a suitable subgroup C. Obviously, C has finite exponent and so
![]() $A^e$
is the largest divisible subgroup of A. If
$A^e$
is the largest divisible subgroup of A. If
![]() $A/B$
is a group of type
$A/B$
is a group of type
![]() $p^\infty $
for some prime p, then
$p^\infty $
for some prime p, then
![]() $A^e$
is also of type
$A^e$
is also of type
![]() $p^\infty $
since it is a nontrivial homomorphic image of
$p^\infty $
since it is a nontrivial homomorphic image of
![]() $A/B$
.
$A/B$
.
Lemma 4.2. Let G be a periodic group and let Q be a permutably embedded p-subgroup of G, where p is a prime number. Then Q is contained in
![]() $\zeta _k(G)$
for some nonnegative integer k.
$\zeta _k(G)$
for some nonnegative integer k.
Proof. Of course, it can be assumed that
![]() $[Q,g]\neq \{1\}$
for a suitable element g of G. Since the subgroup
$[Q,g]\neq \{1\}$
for a suitable element g of G. Since the subgroup
![]() $\langle Q,g\rangle $
is quasihamiltonian, it follows from [Reference Schmidt13, Theorem 2.4.14] that Q has finite exponent e. Let x be an element of Q of order p and let y be an arbitrary element of G. Then
$\langle Q,g\rangle $
is quasihamiltonian, it follows from [Reference Schmidt13, Theorem 2.4.14] that Q has finite exponent e. Let x be an element of Q of order p and let y be an arbitrary element of G. Then
![]() $\langle y\rangle $
is a permutable subgroup of
$\langle y\rangle $
is a permutable subgroup of
![]() $\langle Q,y\rangle $
and so, in particular,
$\langle Q,y\rangle $
and so, in particular,
![]() $\langle y\rangle ^x=\langle y\rangle $
. Thus, x normalises all subgroups of G and hence it belongs to
$\langle y\rangle ^x=\langle y\rangle $
. Thus, x normalises all subgroups of G and hence it belongs to
![]() $\zeta _2(G)$
(see for instance [Reference Schenkman11]). Therefore,
$\zeta _2(G)$
(see for instance [Reference Schenkman11]). Therefore,
![]() $Q\zeta _2(G)/\zeta _2(G)$
has exponent strictly smaller than e and so by induction Q is contained in some term of the upper central series of G with finite ordinal type.
$Q\zeta _2(G)/\zeta _2(G)$
has exponent strictly smaller than e and so by induction Q is contained in some term of the upper central series of G with finite ordinal type.
Corollary 4.3. Let G be a periodic group and let Q be a permutably embedded subgroup of G. Then Q is contained in
![]() $\zeta _\omega (G)$
.
$\zeta _\omega (G)$
.
Proof. Each primary subgroup of Q is permutably embedded in G and so by Lemma 4.2, it is contained in some term with finite ordinal type of the upper central series of G. Therefore,
![]() $Q\leq \zeta _\omega (G)$
.
$Q\leq \zeta _\omega (G)$
.
In relation to the above statement, we notice that a permutably embedded subgroup Q of a periodic group G need not be contained in some term with finite ordinal type of the upper central series of G, even if
![]() $[G/Q]$
is a Černikov lattice. To see this, it is enough to observe that for each prime p, there exists a quasihamiltonian p-group
$[G/Q]$
is a Černikov lattice. To see this, it is enough to observe that for each prime p, there exists a quasihamiltonian p-group
![]() $G_p$
of class p and consider the direct product
$G_p$
of class p and consider the direct product
![]() $G=\mathop {\textrm {Dr}}_pG_p$
, which is quasihamiltonian but not nilpotent. However, it can be proved that if a permutably embedded subgroup Q of a periodic group G determines a Černikov interval of
$G=\mathop {\textrm {Dr}}_pG_p$
, which is quasihamiltonian but not nilpotent. However, it can be proved that if a permutably embedded subgroup Q of a periodic group G determines a Černikov interval of
![]() $\mathfrak {L}(G)$
, then it is always subnormal in G and it lies in some term with finite ordinal type of the upper central series of G provided that it is core-free. To see this, we need the following result.
$\mathfrak {L}(G)$
, then it is always subnormal in G and it lies in some term with finite ordinal type of the upper central series of G provided that it is core-free. To see this, we need the following result.
Lemma 4.4. Let G be a periodic locally nilpotent group and let X be a subgroup of G such that the interval
![]() $[G/X]$
is a Černikov lattice. Then X contains all but finitely many Sylow subgroups of G.
$[G/X]$
is a Černikov lattice. Then X contains all but finitely many Sylow subgroups of G.
Proof. Let
![]() $p_1<p_2<\cdots <p_n<p_{n+1}<\cdots $
be the sequence of all prime numbers. For each positive integer n, let
$p_1<p_2<\cdots <p_n<p_{n+1}<\cdots $
be the sequence of all prime numbers. For each positive integer n, let
![]() $P_n$
be the unique Sylow
$P_n$
be the unique Sylow
![]() $p_n$
-subgroup of G and put
$p_n$
-subgroup of G and put
![]() $G_n=\mathop {\textrm {Dr}}_{k\geq n}P_k$
. Then,
$G_n=\mathop {\textrm {Dr}}_{k\geq n}P_k$
. Then,
is a descending sequence of subgroups of G containing X and so there exists m such that
![]() $XG_n=XG_{n+1}$
for all
$XG_n=XG_{n+1}$
for all
![]() $n\geq m$
. If
$n\geq m$
. If
![]() $X_n$
is the unique Sylow
$X_n$
is the unique Sylow
![]() $p_n$
-subgroup of X, we have
$p_n$
-subgroup of X, we have
![]() $[X_n,G_{n+1}]=\{1\}$
so that
$[X_n,G_{n+1}]=\{1\}$
so that
![]() $X_n$
is normal in
$X_n$
is normal in
![]() $XG_{n+1}$
and
$XG_{n+1}$
and
![]() $XG_{n+1}/X_n$
has no elements of order
$XG_{n+1}/X_n$
has no elements of order
![]() $p_n$
. Thus,
$p_n$
. Thus,
![]() $P_n=X_n\leq X$
for all
$P_n=X_n\leq X$
for all
![]() $n\geq m$
and hence
$n\geq m$
and hence
![]() $G_m$
is contained in X.
$G_m$
is contained in X.
Theorem 4.5. Let G be a periodic group and let Q be a permutably embedded subgroup of G such that the interval
![]() $[G/Q]$
is a Černikov lattice. Then
$[G/Q]$
is a Černikov lattice. Then
![]() $Q/Q_G$
is contained in
$Q/Q_G$
is contained in
![]() $\zeta _k(G/Q_G)$
for some nonnegative integer k. In particular, Q is subnormal in G.
$\zeta _k(G/Q_G)$
for some nonnegative integer k. In particular, Q is subnormal in G.
Proof. By Corollary 4.3, the subgroup Q is contained in
![]() $Z=\zeta _\omega (G)$
. Thus, the subgroup lattice of
$Z=\zeta _\omega (G)$
. Thus, the subgroup lattice of
![]() $G/Z$
is Černikov and so
$G/Z$
is Černikov and so
![]() $G/Z$
is a Černikov group. Let
$G/Z$
is a Černikov group. Let
![]() $J/Z$
be the largest divisible subgroup of
$J/Z$
be the largest divisible subgroup of
![]() $G/Z$
. Then
$G/Z$
. Then
![]() $G/J$
is finite and J is hypercentral so that it follows from Lemma 4.4 that there exists a finite set
$G/J$
is finite and J is hypercentral so that it follows from Lemma 4.4 that there exists a finite set
![]() $\pi $
of prime numbers such that
$\pi $
of prime numbers such that
![]() $\pi (G/J)\subseteq \pi $
and Q contains the
$\pi (G/J)\subseteq \pi $
and Q contains the
![]() $\pi '$
-component
$\pi '$
-component
![]() $J_{\pi '}$
of J. Then
$J_{\pi '}$
of J. Then
![]() $Q_{\pi '}=J_{\pi '}$
is normal in G and
$Q_{\pi '}=J_{\pi '}$
is normal in G and
![]() $G/Q_{\pi '}$
is a
$G/Q_{\pi '}$
is a
![]() $\pi $
-group. Application of Lemma 4.2 to each primary component of
$\pi $
-group. Application of Lemma 4.2 to each primary component of
![]() $Q/Q_{\pi '}$
yields that
$Q/Q_{\pi '}$
yields that
![]() $Q/Q_{\pi '}\leq \zeta _k(G/Q_{\pi '})$
for a suitable nonnegative integer k, and hence
$Q/Q_{\pi '}\leq \zeta _k(G/Q_{\pi '})$
for a suitable nonnegative integer k, and hence
![]() $Q/Q_G$
lies in
$Q/Q_G$
lies in
![]() $\zeta _k(G/Q_G)$
.
$\zeta _k(G/Q_G)$
.
Proof of Theorem 1.2
The subgroup Q is contained in
![]() $\zeta _\omega (G)$
by Corollary 4.3 so that
$\zeta _\omega (G)$
by Corollary 4.3 so that
![]() $G/\zeta _\omega (G)$
is a Černikov group and hence there exists a Černikov normal subgroup W of G such that
$G/\zeta _\omega (G)$
is a Černikov group and hence there exists a Černikov normal subgroup W of G such that
![]() $G/W$
is hypercentral (see [Reference Dixon, Kurdachenko and Otal5, Corollary B4]). Since the hypotheses are inherited by homomorphic images, we may replace G by
$G/W$
is hypercentral (see [Reference Dixon, Kurdachenko and Otal5, Corollary B4]). Since the hypotheses are inherited by homomorphic images, we may replace G by
![]() $G/W$
and assume that G is hypercentral. In particular, G is the direct product of its Sylow subgroups. Put
$G/W$
and assume that G is hypercentral. In particular, G is the direct product of its Sylow subgroups. Put
![]() $\pi =\pi (G/Q)$
. Then the largest
$\pi =\pi (G/Q)$
. Then the largest
![]() $\pi '$
-subgroup
$\pi '$
-subgroup
![]() $G_{\pi '}$
of G is contained in Q and hence it is quasihamiltonian. Clearly, the set
$G_{\pi '}$
of G is contained in Q and hence it is quasihamiltonian. Clearly, the set
![]() $\pi $
is finite and
$\pi $
is finite and
![]() $G=G_\pi \times G_{\pi '}$
so that it is enough to prove that the statement is true for every Sylow subgroup of G. Thus, we may suppose that G is a p-group for some prime number p.
$G=G_\pi \times G_{\pi '}$
so that it is enough to prove that the statement is true for every Sylow subgroup of G. Thus, we may suppose that G is a p-group for some prime number p.
Since Q is quasihamiltonian, it is abelian-by-finite (see [Reference Schmidt13, Theorem 2.4.14]) and so it contains an abelian characteristic subgroup A of finite index (see for instance [Reference Kargapolov and Merzljakov7, Lemma 21.1.4]). Then A is a permutably embedded normal subgroup of G and
![]() $G/A$
is Černikov so that Q can be replaced by A and we may assume that Q is abelian. Moreover, by the results of Černikov and Schlette, we may also suppose that Q is not contained in
$G/A$
is Černikov so that Q can be replaced by A and we may assume that Q is abelian. Moreover, by the results of Černikov and Schlette, we may also suppose that Q is not contained in
![]() $\zeta (G)$
. Thus there exists
$\zeta (G)$
. Thus there exists
![]() $g\in G$
such that
$g\in G$
such that
![]() $\langle g,Q\rangle $
is a nonabelian quasihamiltonian group, whence Q must have finite exponent. It follows from Lemma 4.2 that
$\langle g,Q\rangle $
is a nonabelian quasihamiltonian group, whence Q must have finite exponent. It follows from Lemma 4.2 that
![]() $Q\leq \zeta _k(G)$
for some nonnegative integer k so that the factor group
$Q\leq \zeta _k(G)$
for some nonnegative integer k so that the factor group
![]() $G/\zeta _k(G)$
is Černikov. Therefore,
$G/\zeta _k(G)$
is Černikov. Therefore,
![]() $\gamma _{k+1}(G)$
is also a Černikov group (see [Reference Robinson10, Part 1, Corollary 2 to Theorem 4.21]) and hence it is enough to prove the statement for the factor group
$\gamma _{k+1}(G)$
is also a Černikov group (see [Reference Robinson10, Part 1, Corollary 2 to Theorem 4.21]) and hence it is enough to prove the statement for the factor group
![]() $G/\gamma _{k+1}(G)$
. Thus, we may assume without loss of generality that G is nilpotent.
$G/\gamma _{k+1}(G)$
. Thus, we may assume without loss of generality that G is nilpotent.
Let
![]() $J/Q$
be the largest divisible subgroup of the Černikov group
$J/Q$
be the largest divisible subgroup of the Černikov group
![]() $G/Q$
. Then Q is contained in
$G/Q$
. Then Q is contained in
![]() $\zeta (J)$
by Lemma 3.2 so that
$\zeta (J)$
by Lemma 3.2 so that
![]() $J'$
is Černikov, and again we may replace G by
$J'$
is Černikov, and again we may replace G by
![]() $G/J'$
and assume that J is abelian. Write
$G/J'$
and assume that J is abelian. Write
where each
![]() $J_i/Q$
is a group of type
$J_i/Q$
is a group of type
![]() $p^\infty $
. It follows from Lemma 4.1 that
$p^\infty $
. It follows from Lemma 4.1 that
![]() $J_i=P_i\times B_i$
, where
$J_i=P_i\times B_i$
, where
![]() $P_i$
is a group of type
$P_i$
is a group of type
![]() $p^\infty $
and
$p^\infty $
and
![]() $B_i$
has finite exponent i (
$B_i$
has finite exponent i (
![]() $i=1,\ldots ,t$
). Since G is nilpotent,
$i=1,\ldots ,t$
). Since G is nilpotent,
![]() $J/Q$
lies in
$J/Q$
lies in
![]() $\zeta (G/Q)$
so that each
$\zeta (G/Q)$
so that each
![]() $J_i$
is normal in G and hence also
$J_i$
is normal in G and hence also
![]() $P_i$
is normal in G for every
$P_i$
is normal in G for every
![]() $i=1,\ldots ,t$
. It follows that
$i=1,\ldots ,t$
. It follows that
![]() $P=\langle P_1,\ldots ,P_t\rangle $
is a Černikov normal subgroup of G. Moreover,
$P=\langle P_1,\ldots ,P_t\rangle $
is a Černikov normal subgroup of G. Moreover,
![]() $J/P$
has finite exponent and so
$J/P$
has finite exponent and so
![]() $J=PQ$
. Therefore,
$J=PQ$
. Therefore,
![]() $J/P$
is a permutably embedded subgroup of finite index of
$J/P$
is a permutably embedded subgroup of finite index of
![]() $G/P$
and hence
$G/P$
and hence
![]() $G/P$
contains a finite normal subgroup
$G/P$
contains a finite normal subgroup
![]() $N/P$
such that
$N/P$
such that
![]() $G/N$
is quasihamiltonian (see [Reference De Falco, de Giovanni and Musella2, Theorem 3.5]). Since N is Černikov, the proof is complete.
$G/N$
is quasihamiltonian (see [Reference De Falco, de Giovanni and Musella2, Theorem 3.5]). Since N is Černikov, the proof is complete.