Article contents
Finite groups with large centralizers
Published online by Cambridge University Press: 17 April 2009
Abstract
It is known that a finite non-abelian group G has a proper centralizer of order 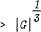 if, for example, |G| is even and |Z(G)| is odd, or whenever G is solvable. Often the exponent
if, for example, |G| is even and |Z(G)| is odd, or whenever G is solvable. Often the exponent 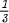 can be improved to
can be improved to 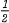 , for example when G is supersolvable, or metabelian, or |G = pαqβ. Here we show more generally that this improvement is possible in many situations where G is factorizable into the product of two subgroups. In particular, much more evidence is presented to support the conjecture that some proper centralizer has order
, for example when G is supersolvable, or metabelian, or |G = pαqβ. Here we show more generally that this improvement is possible in many situations where G is factorizable into the product of two subgroups. In particular, much more evidence is presented to support the conjecture that some proper centralizer has order 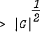 whenever G is a finite non-abelian solvable group.
whenever G is a finite non-abelian solvable group.
- Type
- Research Article
- Information
- Bulletin of the Australian Mathematical Society , Volume 32 , Issue 3 , December 1985 , pp. 399 - 414
- Copyright
- Copyright © Australian Mathematical Society 1985
References
- 1
- Cited by




