Hostname: page-component-8448b6f56d-jr42d Total loading time: 0 Render date: 2024-04-23T20:35:06.218Z Has data issue: false hasContentIssue false
  • English
  • Français

EXISTENCE AND BOX DIMENSION OF GENERAL RECURRENT FRACTAL INTERPOLATION FUNCTIONS

Part of: Approximations and expansions Classical measure theory

Published online by Cambridge University Press:  05 October 2020

HUO-JUN RUAN Open the ORCID record for HUO-JUN RUAN [Opens in a new window] ,
JIAN-CI XIAO Open the ORCID record for JIAN-CI XIAO [Opens in a new window]  and
BING YANG Open the ORCID record for BING YANG [Opens in a new window]
HUO-JUN RUAN*
Affiliation:
School of Mathematical Sciences, Zhejiang University, Hangzhou 310027, China
JIAN-CI XIAO
Affiliation:
School of Mathematical Sciences, Zhejiang University, Hangzhou 310027, China e-mail: jcxshaw24@zju.edu.cn
BING YANG
Affiliation:
Department of Mathematics, University of Nottingham Ningbo China, Ningbo 315100, China e-mail: bingyangmath@163.com
*
e-mail: ruanhj@zju.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

The notion of recurrent fractal interpolation functions (RFIFs) was introduced by Barnsley et al. [‘Recurrent iterated function systems’, Constr. Approx. 5 (1989), 362–378]. Roughly speaking, the graph of an RFIF is the invariant set of a recurrent iterated function system on 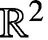$\mathbb {R}^2$. We generalise the definition of RFIFs so that iterated functions in the recurrent system need not be contractive with respect to the first variable. We obtain the box dimensions of all self-affine RFIFs in this general setting.

Keywords

box dimensioniterated function systemsrecurrent fractal interpolation functionsstrongly connected component

MSC classification

Primary: 28A80: Fractals
Secondary: 41A30: Approximation by other special function classes
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 103 , Issue 2 , April 2021 , pp. 278 - 290
Check for updates
Copyright
© 2020 Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The research is supported by the NSFC grant 11771391.

References

Bárány, B., Rams, M. and Simon, K., ‘Dimension theory of some non-Markovian repellers. Part I: A gentle introduction’, Preprint, 2019, arXiv:1901.04035.Google Scholar
Bárány, B., Rams, M. and Simon, K., ‘Dimension theory of some non-Markovian repellers. Part II: Dynamically defined function graphs’, Preprint, 2019, arXiv:1901.04037.Google Scholar
Barnsley, M. F., ‘Fractal functions and interpolation’, Constr. Approx. 2 (1986), 303–329.10.1007/BF01893434CrossRefGoogle Scholar
Barnsley, M. F., Elton, J. and Hardin, D., ‘Recurrent iterated function systems’, Constr. Approx. 5 (1989), 362–378.CrossRefGoogle Scholar
Barnsley, M. F., Harding, B., Vince, A. and Viswanathan, P., ‘Approximation of rough functions’, J. Approx. Theory 209 (2016), 23–43.10.1016/j.jat.2016.04.003CrossRefGoogle Scholar
Barnsley, M. and Massopust, P., ‘Bilinear fractal interpolation and box dimension’, J. Approx. Theory 192 (2015), 362–378.CrossRefGoogle Scholar
Bouboulis, P. and Dalla, L., ‘A general construction of fractal interpolation functions on grids of ${\mathbb{R}}^n$ ’, European J. Appl. Math. 18 (2007), 449–476.CrossRefGoogle Scholar
Hardin, D. P. and Massopust, P. R., ‘The capacity of a class of fractal functions’, Comm. Math. Phys. 105 (1986), 455–460.CrossRefGoogle Scholar
Horn, R. and Johnson, C., Matrix Analysis (Cambridge University Press, Cambridge, UK, 1985).CrossRefGoogle Scholar
Kong, Q. G., Ruan, H. J. and Zhang, S., ‘Box dimension of bilinear fractal interpolation surfaces’, Bull. Aust. Math. Soc. 98 (2018), 113–121.CrossRefGoogle Scholar
Liang, Z. and Ruan, H.-J., ‘Construction and box dimension of recurrent fractal interpolation surfaces’, Preprint, 2019, arXiv:1902.01165.CrossRefGoogle Scholar
Małysz, R., ‘The Minkowski dimension of the bivariate fractal interpolation surfaces’, Chaos Solitons Fractals 27 (2006), 1147–1156.10.1016/j.chaos.2005.05.007CrossRefGoogle Scholar
Mazel, D. S. and Hayes, M. H., ‘Using iterated function systems to model discrete sequences’, IEEE Trans. Signal Process. 40 (1992), 1724–1734.CrossRefGoogle Scholar
Ruan, H. J., Su, W. Y. and Yao, K., ‘Box dimension and fractional integral of linear fractal interpolation functions’, J. Approx. Theory 161 (2009), 187–197.CrossRefGoogle Scholar