No CrossRef data available.
Article contents
THE DIFFERENCE ANALOGUE OF THE TUMURA–HAYMAN–CLUNIE THEOREM
Part of:
Difference and functional equations
Entire and meromorphic functions, and related topics
Difference equations
Published online by Cambridge University Press: 06 November 2023
Abstract
We prove a difference analogue of the celebrated Tumura–Hayman–Clunie theorem. Let f be a transcendental entire function, let c be a nonzero constant and let n be a positive integer. If f and 
$\Delta _c^n f$ omit zero in the whole complex plane, then either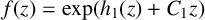 
$f(z)=\exp (h_1(z)+C_1 z)$, where 
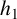$h_1$ is an entire function of period c and 
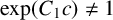$\exp (C_1 c)\neq 1$, or 
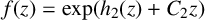$f(z)=\exp (h_2(z)+C_2 z)$, where 
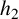$h_2$ is an entire function of period 
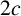$2c$ and 
$C_2$ satisfies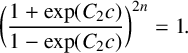 
$$ \begin{align*} \bigg(\frac{1+\exp(C_2c)}{1-\exp(C_2 c)}\bigg)^{2n}=1. \end{align*} $$
MSC classification
Secondary:
39A10: Difference equations, additive
- Type
- Research Article
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.
Footnotes
This work was partially supported by the National Natural Science Foundation of China (Grant Nos. 12171127, 12071047, 12301096, 11901311, 12371074) and National Key Technologies R&D Program of China (2020YFA0713300).
References
Chen, Z. X., ‘Relationships between entire functions and their forward differences’, Complex Var. Elliptic Equ. 58(3) (2013), 299–307.CrossRefGoogle Scholar
Chen, Z. X. and Shon, K. H., ‘Estimates for the zeros of differences of meromorphic functions’, Sci. China Ser. A 52(11) (2009), 2447–2458.CrossRefGoogle Scholar
Chiang, Y. M. and Feng, S. J., ‘On the Nevanlinna characteristic of
$f(z+\eta)$
and difference equations in the complex plane’, Ramanujan J. 16(1) (2008), 105–129.CrossRefGoogle Scholar
$f(z+\eta)$
and difference equations in the complex plane’, Ramanujan J. 16(1) (2008), 105–129.CrossRefGoogle ScholarChiang, Y. M. and Feng, S. J., ‘On the growth of logarithmic differences, difference quotients and logarithmic derivatives of meromorphic functions’, Trans. Amer. Math. Soc. 361 (2009), 3767–3791.CrossRefGoogle Scholar
Clunie, J., ‘On integral and meromorphic functions’, J. Lond. Math. Soc. 37 (1962), 17–27.CrossRefGoogle Scholar
Csillag, P., ‘Über ganze Funktionen, welehe drei nicht verschwindende Ableitungen besitzen’, Math. Ann. 110 (1935), 745–752.CrossRefGoogle Scholar
Frank, G., ‘Eine Vermutung von Hayman über Nullstellen meromorpher Funktionen’, Math. Z. 149 (1976), 29–36.CrossRefGoogle Scholar
Halburd, R. G. and Korhonen, R. J., ‘Difference analogue of the lemma on the logarithmic derivative with applications to difference equations’, J. Math. Anal. Appl. 314(2) (2006), 477–487.CrossRefGoogle Scholar
Halburd, R. G. and Korhonen, R. J., ‘Nevanlinna theory for the difference operator’, Ann. Acad. Sci. Fenn. Math. 31(2) (2006), 463–478.Google Scholar
Halburd, R. G., Korhonen, R. J. and Tohge, K., ‘Holomorphic curves with shift-invariant hyperplane preimages’, Trans. Amer. Math. Soc. 366(8) (2014), 4267–4298.CrossRefGoogle Scholar
Hayman, W. K., ‘Picard values of meromorphic functions and their derivatives’, Ann. of Math. 70(2) (1959), 9–42.CrossRefGoogle Scholar
Hayman, W. K., Meromorphic Functions, Oxford Mathematical Monographs, 3 (Clarendon Press, Oxford, 1964).Google Scholar
Langley, J. K., ‘Proof of a conjecture of Hayman concerning
$f$
and
${f}^{{\prime\prime} }$
’, J. Lond. Math. Soc. 48(2) (1993), 500–514.CrossRefGoogle Scholar
$f$
and
${f}^{{\prime\prime} }$
’, J. Lond. Math. Soc. 48(2) (1993), 500–514.CrossRefGoogle ScholarPólya, G., ‘On an integral function of an integral function’, J. Lond. Math. Soc. 1(1) (1926), 12–15.CrossRefGoogle Scholar
Tumura, Y., ‘On the extensions of Borel’s theorem and Saxer–Csillag’s theorem’, Proc. Phys. Math. Soc. Japan 19(3) (1937), 29–35.Google Scholar
Yang, C. C. and Yi, H. X., Uniqueness Theory of Meromorphic Functions (Kluwer Academic Publishers and Science Press, Dordrecht–Beijing–New York, 2003).CrossRefGoogle Scholar