Hostname: page-component-848d4c4894-v5vhk Total loading time: 0 Render date: 2024-06-25T17:17:40.715Z Has data issue: false hasContentIssue false
  • English
  • Français

CONGRUENCES FOR RANKS OF PARTITIONS

Part of: Discontinuous groups and automorphic forms Combinatorics Additive number theory; partitions

Published online by Cambridge University Press:  29 January 2024

RENRONG MAO
RENRONG MAO*
Affiliation:
Department of Mathematics, Soochow University, Suzhou 215006, PR China
*
e-mail: rrmao@suda.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

Ranks of partitions play an important role in the theory of partitions. They provide combinatorial interpretations for Ramanujan’s famous congruences for partition functions. We establish a family of congruences modulo powers of 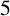$5$ for ranks of partitions.

Keywords

partitionsrankscongruencesmodular functions

MSC classification

Primary: 11P83: Partitions; congruences and congruential restrictions
Secondary: 05A17: Partitions of integers 11F30: Fourier coefficients of automorphic forms 11F37: Forms of half-integer weight; nonholomorphic modular forms
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , First View , pp. 1 - 11
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

This work is supported by NSFC (National Natural Science Foundation of China) through Grant No. NSFC 12071331.

References

Andrews, G. E., Berndt, B. C., Chan, S. H., Kim, S. and Malik, A., ‘Four identities for third order mock theta functions’, Nagoya Math. J. 239 (2020), 173–204.CrossRefGoogle Scholar
Andrews, G. E. and Lewis, R., ‘The ranks and cranks of partitions moduli $2$ , $3$ , and $4$ ’, J. Number Theory 85(1) (2000), 74–84.CrossRefGoogle Scholar
Atkin, A. O. L. and Swinnerton-Dyer, H. P. F., ‘Some properties of partitions’, Proc. Lond. Math. Soc. (3) 4 (1954), 84–106.CrossRefGoogle Scholar
Bringmann, K., ‘Asymptotics for rank partition functions’, Trans. Amer. Math. Soc. 361(7) (2009), 3483–3500.CrossRefGoogle Scholar
Bringmann, K. and Kane, B., ‘Inequalities for differences of Dyson’s rank for all odd moduli’, Math. Res. Lett. 17(5) (2010), 927–942.CrossRefGoogle Scholar
Bringmann, K. and Mahlburg, K., ‘Inequalities between ranks and cranks’, Proc. Amer. Math. Soc. 137(8) (2009), 2567–2574.CrossRefGoogle Scholar
Chan, S. and Mao, R., ‘The rank and crank of partitions modulo $3$ ’, Int. J. Number Theory 12(4) (2016), 1027–1053.CrossRefGoogle Scholar
Chen, D., Chen, R. and Garvan, F., ‘Congruences modulo powers of 5 for the rank parity functions’, Hardy-Ramanujan J. 43 (2020), 24–45.Google Scholar
Dyson, F. J., ‘Some guesses in the theory of partitions’, Eureka 8 (1944), 10–15.Google Scholar
Fan, Y., Xia, E. X. W. and Zhao, X., ‘New equalities and inequalities for the ranks and cranks of partitions’, Adv. Appl. Math. 146 (2023), Article no. 102486.CrossRefGoogle Scholar
Garvan, F. G., ‘A tutorial for the MAPLE ETA package’, Preprint, 2019, arXiv:1907.09130.Google Scholar
Lewis, R., ‘On the ranks of partitions modulo $9$ ’, Bull. Lond. Math. Soc. 23(5) (1991), 417–421.CrossRefGoogle Scholar
Mao, R., ‘Ranks of partitions modulo $10$ ’, J. Number Theory 133 (2013), 3678–3702.CrossRefGoogle Scholar
Mao, R. and Zhou, Z., ‘Congruences modulo powers of $5$ for odd ranks’, Preprint.Google Scholar
Newman, M., ‘Construction and application of a class of modular functions. II’, Proc. Lond. Math. Soc. (3) 9 (1959), 373–387.CrossRefGoogle Scholar
Paule, P. and Radu, S., ‘The Andrews–Sellers family of partition congruences’, Adv. Math. 230(3) (2012), 819–838.CrossRefGoogle ScholarPubMed
Santa-Gadea, N., ‘On some relations for the rank moduli $9$ and $12$ ’, J. Number Theory 40(2) (1992), 130–145.Google Scholar
Wang, L. and Yang, Y., ‘The smallest parts function associated with $\omega (q)$ ’, Int. J. Number Theory 18(10) (2022), 2279–2297.CrossRefGoogle Scholar