Hostname: page-component-77c89778f8-9q27g Total loading time: 0 Render date: 2024-07-20T05:19:24.332Z Has data issue: false hasContentIssue false
  • English
  • Français

Composition operators on weighted Bergman-Orlicz spaces

Published online by Cambridge University Press:  17 April 2009

Ajay K. Sharma  and
S. D. Sharma
Ajay K. Sharma
Affiliation:
Department of Applied Physics and Mathematics, Shri Mata Vaishno Devi University, Jammu–180006, India, e-mail: aksju_76@yahoo.com
S. D. Sharma
Affiliation:
Department of Mathematics, University of Jammu, Jammu–180006, India, e-mail: somdatt_jammu@yahoo.co.in
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper, composition operators acting on Bergman-Orlicz spaces

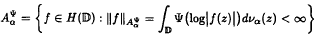
are studied, where ψ is a non-constant, non-decreasing convex function defined on (-∞, ∞) which satisfies the growth condition 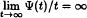. In fact, under a mild condition on ∞, we show that every holomorphic-self map ∞ of 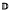induces a bounded composition operator on 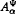and C∞ is compact on 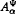if and only if it is compact on .

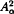Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 75 , Issue 2 , April 2007 , pp. 273 - 287
Copyright
Copyright © Australian Mathematical Society 2007

References

[1]Axler, S., ‘Bergman spaces and their operators’, in Surveys of some recent results in operator theory, Vol. 1, Pitman Research Notes in Math. 171 (Longman Science and Technology, Harlow, 1988), pp. 1–50.Google Scholar
[2]Cima, J. and Matheson, A., ‘Essential norms of a Composition operators and Aleksandrov Measures’, Pacific J. Math. 179 (1997), 59–63.CrossRefGoogle Scholar
[3]Hasumi, M. and Kataoka, S., ‘Remarks on Hardy–Orlicz classes’, Arch. Math. 51 (1988), 455–463.CrossRefGoogle Scholar
[4]MacCluer, B.D. and Shapiro, J.H., ‘Angular derivatives and compact composition operators on Hardy and Bergman spaces’, Canad. J. Math. 38 (1986), 878–906.CrossRefGoogle Scholar
[5]Schwartz, H.J., Composition operators on HP, (Thesis) (University of Toledo, 1969).Google Scholar
[6]Shapiro, J.H. and Sundberg, C., ‘Compact composition operators on L 1’, Proc. Amer. Math. Soc. 108 (1990), 443–449.Google Scholar
[7]Shapiro, J.H. and Taylor, P.D., ‘Compact, nuclear and Hilbert-Schmidt composition operators on H 2’, Indiana Univ. Math. J. 23 (1973), 471–496.CrossRefGoogle Scholar
[8]Shapiro, J.H., ‘The essential norm of a composition operator’, Ann. of Math. (2) 125 (1987), 375–404.CrossRefGoogle Scholar
[9]Shapiro, J.H., Composition operators and classical function theory (Springer-Verlag, New York, 1993).CrossRefGoogle Scholar
[10]Stevic, S., ‘On generalised weighted Bergman spaces’, Complex Var. Theory. Appl. 49 (2004), 109–124.Google Scholar