Article contents
CENTRALISERS IN THE INFINITE SYMMETRIC INVERSE SEMIGROUP
Published online by Cambridge University Press: 28 September 2012
Abstract
For an arbitrary set 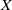 $X$ (finite or infinite), denote by
$X$ (finite or infinite), denote by 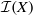 $\mathcal {I}(X)$ the symmetric inverse semigroup of partial injective transformations on
$\mathcal {I}(X)$ the symmetric inverse semigroup of partial injective transformations on 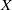 $X$. For
$X$. For  $ \alpha \in \mathcal {I}(X)$, let
$ \alpha \in \mathcal {I}(X)$, let 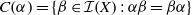 $C(\alpha )=\{ \beta \in \mathcal {I}(X): \alpha \beta = \beta \alpha \}$ be the centraliser of
$C(\alpha )=\{ \beta \in \mathcal {I}(X): \alpha \beta = \beta \alpha \}$ be the centraliser of  $ \alpha $ in
$ \alpha $ in 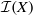 $\mathcal {I}(X)$. For an arbitrary
$\mathcal {I}(X)$. For an arbitrary  $ \alpha \in \mathcal {I}(X)$, we characterise the transformations
$ \alpha \in \mathcal {I}(X)$, we characterise the transformations 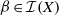 $ \beta \in \mathcal {I}(X)$ that belong to
$ \beta \in \mathcal {I}(X)$ that belong to 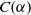 $C( \alpha )$, describe the regular elements of
$C( \alpha )$, describe the regular elements of 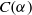 $C(\alpha )$, and establish when
$C(\alpha )$, and establish when 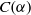 $C( \alpha )$ is an inverse semigroup and when it is a completely regular semigroup. In the case where
$C( \alpha )$ is an inverse semigroup and when it is a completely regular semigroup. In the case where 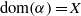 $\operatorname {dom}( \alpha )=X$, we determine the structure of
$\operatorname {dom}( \alpha )=X$, we determine the structure of 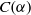 $C(\alpha )$in terms of Green’s relations.
$C(\alpha )$in terms of Green’s relations.
MSC classification
- Type
- Research Article
- Information
- Copyright
- Copyright © 2012 Australian Mathematical Publishing Association Inc.
References
- 4
- Cited by




