Hostname: page-component-84b7d79bbc-dwq4g Total loading time: 0 Render date: 2024-07-30T19:14:15.144Z Has data issue: false hasContentIssue false
  • English
  • Français

Arithmetic on certain families of elliptic curves

Published online by Cambridge University Press:  17 April 2009

Andrzej Dabrowski  and
Małgorzata Wieczorek
Andrzej Dabrowski
Affiliation:
University of Szczecin, Institute of Mathematics, ul. Wielkopolska 15, 70-451 Szczecin, Poland e-mail: dabrowsk@sus.univ.szczecin.pl
Małgorzata Wieczorek
Affiliation:
University of Szczecin, Institute of Mathematics, ul. Wielkopolska 15, 70-451 Szczecin, Poland e-mail: dabrowsk@sus.univ.szczecin.pl
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Consider a family of elliptic curves 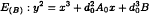(A, A0, d0 fixed integers). We prove that, under certain conditions on A0 and d0, the rational torsion subgroup of E(B) is either cyclic of order ≤ 3 or non-cyclic of order 4. Also, assuming standard conjectures, we establish estimates for the order of the Tate-Shafarevich groups as B varies.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 61 , Issue 2 , April 2000 , pp. 319 - 327
Copyright
Copyright © Australian Mathematical Society 2000

References

REFERENCES

[1]Cremona, J.E., Algorithms for modular elliptic curves (Cambridge University Press, Cambridge, 1992).Google Scholar
[2]Dabrowski, A. and Pomykała, J., ‘On the order of the Tate-Shafarevich group in a quadratic family of elliptic curves’, (submitted).Google Scholar
[3]Goldfeld, D., Hoffstein, J. and Patterson, S.J., ‘On automorphic functions of half-integral weight with applications to elliptic curves’, in Number Theory Related to Fermat's Last Theorem (Birkhäuser, Boston, MA, 1982), pp. 153–193.CrossRefGoogle Scholar
[4]Iwaniec, H., ‘Almost-primes represented by quadratic polynomials’, Invent. Math 47 (1978), 171–188.CrossRefGoogle Scholar
[5]Kubert, D.S., ‘Universal bounds on the torsion of elliptic curves’, Proc. London Math. Soc 33 (1976), 193–237.CrossRefGoogle Scholar
[6]Lang, S., ‘Conjectured diophantine estimates on elliptic cures’, in Arithmetic and Geometry - Papers dedicated to I.R. Shafarevich 1 (Birkhäuser, Boston, MA, 1983), pp. 155–171.Google Scholar
[7]Lieman, D., ‘Nonvanishing of L-series associated to cubic twists of elliptic curves’, Ann. Math 140 (1994), 81–108.CrossRefGoogle Scholar
[8]Mai, L. and Murty, M.R., ‘A note on quadratic twists of an elliptic curve’, in CRM Proc. Lecture Notes 4 (American Mathematical Society, Providence, RI, 1994), pp. 121–124.Google Scholar
[9]Mazur, B., ‘Rational isogenies of prime degree’, Invent. Math 44 (1978), 129–162.CrossRefGoogle Scholar
[10]Olson, L.D., ‘Torsion points on elliptic curves with given j-invariant’, Manuscripta Math 16 (1975), 145–150.CrossRefGoogle Scholar
[11]Rohrlich, D.E., ‘Variation of the root number in families of elliptic curves’, Compositio Math 87 (1993), 119–151.Google Scholar
[12]Silverman, J., The arithmetic of elliptic curves, Springer-Verlag Graduate Texts in Mathematics 106 (Springer-Verlag, Berlin, Heidelber, New York, 1986).CrossRefGoogle Scholar
[13]Tate, J., ‘Algorithms for determining the type of a singular type in an elliptic pencil’ in Modular Functions of One Variable IV, Lecture Notes in Mathematics 476 (Springer-Verlag, Berlin, Heidelberg, New York, 1972), pp. 33–52.CrossRefGoogle Scholar
[14]Tunnell, J., ‘A classical diophantine problem and modular forms of weight 3/2’, Invent. Math 72 (1983), 323–334.Google Scholar