Hostname: page-component-5c6d5d7d68-txr5j Total loading time: 0 Render date: 2024-08-16T15:45:24.719Z Has data issue: false hasContentIssue false
  • English
  • Français

Analogues of the Liouville theorem for linear fractional relations in Banach spaces

Published online by Cambridge University Press:  17 April 2009

V.A. Khatskevich ,
M.I. Ostrovskii  and
V.S. Shulman
V.A. Khatskevich
Affiliation:
Department of Mathematics, ORT Braude College, College Campus, P.O. Box, 78, Karmiel 21982, ISRAEL, e-mail: victor_kh@hotmail.com
M.I. Ostrovskii
Affiliation:
Department of Mathematics and Computer Science, St.-John's University, 8000 Utopia Parkway, Queens, NY 11439, United States of America, e-mail: ostrovsm@stjohns.edu
V.S. Shulman
Affiliation:
Department of Mathematics, Vologda State Technical University, 15 Lenina str., Vologda 160000, Russia, e-mail: shulam_v@yahoo.com
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Consider a bounded linear operator T between Banach spaces ℬ, ℬ′ which can be decomposed into direct sums ℬ = ℬ1 ⌖ ℬ2, ℬ′ = ℬ1′ ⌖ ℬ2′. Such linear operator can be represented by a 2 × 2 operator matrix of the form 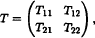where Tij ∈ ℒ(ℬj, ℒi′) i, j = 1, 2. (By ℒ(ℬj, ℒi′) we denote the space of bounded linear operators acting from ℬj to ℬi′ (i, j = 1, 2).) The map GT from L (B1, B2) into the set of closed affine subspaces of ℒ(ℬ1′ ℬ2′), defined by 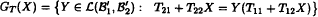is called a linear fractional relation associated with T.

Such relations can be considered as a generalisation of linear fractional transformations which were studied by many authors and found many applications. Many traditional and recently discovered areas of application of linear fractional transformations would benefit from a better understanding of the behaviour of linear fractional relations. The present paper is devoted to analogues of the Liouville theorem “a bounded entire function is constant” for linear fractional relations.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 73 , Issue 1 , February 2006 , pp. 89 - 105
Copyright
Copyright © Australian Mathematical Society 2006

References

Referenes

[1]Alpay, D. and Khatskevich, V., ‘Linear fractional transformations: basic properties, applications to spaces of analytic functions and Schroeder's equation’, Int. J. Appl. Math. 2 (2000), 459–476.Google Scholar
[2]Azizov, T.Ya. and Iokhvidov, I.S., Linear operators in spaces with an indefinite metric (John Wiley and Sons, Chichester, 1989).Google Scholar
[3]Cowen, C.C., ‘Iteration and the solution of functional equations for functions analytic in the unit disk’, Trans. Amer. Math. Soc. 265 (1981), 69–95.CrossRefGoogle Scholar
[4]Cowen, C.C. and MacCluer, B.D., ‘Linear fractional maps of the ball and their composition operators’, Acta Sci. Math. (Szeged) 66 (2000), 351–376.Google Scholar
[5]Dunford, N. and Schwartz, J.T., Linear operators, Part I: General Theory (Interscience Publishers, New York, 1958).Google Scholar
[6]Elin, M. and Khatskevich, V., ‘Triangular plus-operators in Banach spaces: applications to the Koenigs embedding problem’, J. Nonlinear Convex Anal. 6 (2005), 173–185.Google Scholar
[7]Helton, J.W., ‘Operators unitary in an indefinite metric and linear fractional transformations’, Acta Sci. Math. (Szeged) 32 (1971), 261–266.Google Scholar
[8]Iohvidov, I.S., Kreĭn, M.G. and Langer, H., Introduction to the spectral theory of operators in spaces with an indefinite metric (Akademie-Verlag, Berlin, 1982).Google Scholar
[9]Khatskevich, V.A., ‘Fixed points of generalized linear-fractional transformations’, (in Russian), Izv. Akad. Nauk SSSR Ser. Mat. 39 (1975), 1130–1141.Google Scholar
[10]Khatskevich, V., ‘Some global properties of fractional-linear transformations’, in Non-selfadjoint operators and related topics (Beer Sheva, 1992), Oper. Theory Adv. Appl. 73 (Birkhäuser, Basel, 1994), pp. 355–361.CrossRefGoogle Scholar
[11]Khatskevich, V., ‘Generalized fractional linear transformations: convexity and compactness of the image and the pre-image; applications’, Studia Math. 137 (1999), 169–175.CrossRefGoogle Scholar
[12]Khatskevich, V.A., Ostrovskii, M.I. and Shulman, V.S., ‘Linear fractional relations for Hilbert space operators’, Math. Nachrichten (to appear).Google Scholar
[13]Khatskevich, V., Reich, S. and Shoikhet, D., ‘One-parameter semigroups of fractional-linear transformations’, in Operator theory, system theory and related topics (Beer-Sheva/Rehovot, 1997), Oper. Theory Adv. Appl. 123 (Birkhäuser, Basel, 2001), pp. 401–411.CrossRefGoogle Scholar
[14]Khatskevich, V., Reich, S. and Shoikhet, D., ‘Abel-Schröder equations for linear fractional mappings and the Koenigs embedding problem’, Acta Sci. Math. (Szeged) 69 (2003), 67–98.Google Scholar
[15]Khatskevich, V. and Senderov, V., ‘Basic properties of linear fractional mappings of operator balls: Schroeder's equation’, in Operator theory and its applications (Winnipeg, MB, 1998), Fields Inst. Commun. 25 (Amer. Math. Soc., Providence, RI, 2000), pp. 331–344.Google Scholar
[16]Krein, M.G., ‘On an application of the fixed point principle in the theory of linear transformations of spaces with an indefinite metric’, (in Russian), Uspehi Matem. Nauk (N.S.) 36 (1950), 180–190.Google Scholar
[17]Krein, M.G., ‘A new application of the fixed-point principle in the theory of operators in a space with indefinite metric’, (in Russian), Dokl. Akad. Nauk SSSR 154 (1964), 1023–1026.Google Scholar
[18]Krein, M.G. and Smuljan, J.L., ‘Plus-operators in a space with indefinite metric’, (in Russian), Matem. Issled. 1 (1966), 131–161. English translation Amer. Math. Soc. Transl. 85 (1969), 93–113.Google Scholar
[19]Krein, M.G. and Smuljan, J.L., ‘-polar representation of plus-operators’, (in Russian), Matem. Issled. 1 (1966), 172–210. English translation Amer. Math. Soc. Transl. 85 (1969), 115–143.Google Scholar
[20]Krein, M.G. and Smuljan, J.L., ‘On linear-fractional transformations with operator coefficients’, (in Russian), Matem. Issled. 2 (1967), 64–96. English translation Amer. Math. Soc. Transl. 103 (1974), 125–152.Google Scholar
[21]Lindenstrauss, J. and Tzafriri, L., Classical Banach spaces, Lecture Notes in Math. 338 (Springer-Verlag, Berlin, 1973).Google Scholar
[22]Vesentini, E., ‘Semigroups of linear contractions for an indefinite metric’, Atti. Acad. Naz. Lincei Cl. Sci. Fis. Mat. Natur. Mem. (9) Mat. Appl. 2 (1994), 53–83.Google Scholar