Hostname: page-component-76fb5796d-skm99 Total loading time: 0 Render date: 2024-04-26T08:27:14.877Z Has data issue: false hasContentIssue false
  • English
  • Français

ALGEBRAIC NUMBERS WITH BOUNDED DEGREE AND WEIL HEIGHT

Part of: Algebraic number theory: global fields

Published online by Cambridge University Press:  18 July 2018

ARTŪRAS DUBICKAS Open the ORCID record for ARTŪRAS DUBICKAS [Opens in a new window]
ARTŪRAS DUBICKAS*
Affiliation:
Institute of Mathematics, Faculty of Mathematics and Informatics, Vilnius University, Naugarduko 24, LT-03225 Vilnius, Lithuania email arturas.dubickas@mif.vu.lt
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

For a positive integer 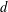$d$ and a nonnegative number 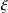$\unicode[STIX]{x1D709}$, let 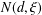$N(d,\unicode[STIX]{x1D709})$ be the number of 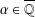$\unicode[STIX]{x1D6FC}\in \overline{\mathbb{Q}}$ of degree at most 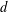$d$ and Weil height at most 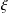$\unicode[STIX]{x1D709}$. We prove upper and lower bounds on 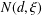$N(d,\unicode[STIX]{x1D709})$. For each fixed 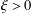$\unicode[STIX]{x1D709}>0$, these imply the asymptotic formula 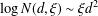$\log N(d,\unicode[STIX]{x1D709})\sim \unicode[STIX]{x1D709}d^{2}$ as 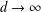$d\rightarrow \infty$, which was conjectured in a question at Mathoverflow [https://mathoverflow.net/questions/177206/].

Keywords

Mahler measureWeil heightcounting functionirreducible polynomial

MSC classification

Primary: 11R06: PV-numbers and generalizations; other special algebraic numbers; Mahler measure
Secondary: 11R09: Polynomials (irreducibility, etc.)
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 98 , Issue 2 , October 2018 , pp. 212 - 220
Copyright
© 2018 Australian Mathematical Publishing Association Inc. 

Footnotes

This research was funded by the European Social Fund according to the activity Improvement of researchers qualification by implementing world-class R&D projects of Measure no. 09.3.3-LMT-K-712-01-0037.

References

Barroero, F., ‘Algebraic S-integers of fixed degree and bounded height’, Acta Arith. 167 (2015), 67–90.Google Scholar
Chern, S.-J. and Vaaler, J. D., ‘The distribution of values of Mahler’s measure’, J. reine angew. Math. 540 (2001), 1–47.Google Scholar
Dubickas, A., ‘Nonreciprocal algebraic numbers of small measure’, Comm. Math. Univ. Carolin. 45 (2004), 693–697.Google Scholar
Dubickas, A., ‘Bounding univariate and multivariate reducible polynomials with restricted height’, Period. Math. Hungar., to appear.Google Scholar
Dubickas, A. and Jankauskas, J., ‘Nonreciprocal algebraic numbers of small Mahler’s measure’, Acta Arith. 157 (2013), 357–364.Google Scholar
Dubickas, A. and Konyagin, S. V., ‘On the number of polynomials of bounded measure’, Acta Arith. 86 (1998), 325–342.Google Scholar
Erdős, P., ‘On the normal number of prime factors of p - 1 and some other related problems concerning Euler’s 𝜙-function’, Quart. J. Math. (Oxford Ser.) 6 (1935), 205–213.Google Scholar
Erdős, P., ‘On pseudoprimes and Carmichael numbers’, Publ. Math. Debrecen 4 (1956), 201–206.Google Scholar
Grizzard, R. and Gunther, J., ‘Slicing the stars: counting algebraic numbers, integers, and units by degree and height’, Algebra and Number Theory 11 (2017), 1385–1436.Google Scholar
Masser, D. and Vaaler, J. D., ‘Counting algebraic numbers with large height. I’, in: Diophantine Approximation, Festschrift for Wolfgang Schmidt, Developments in Mathematics, vol. 16 (eds. Schlickewei, H. P. et al. ) (Springer, Vienna, 2008), 237–243.Google Scholar
Masser, D. and Vaaler, J. D., ‘Counting algebraic numbers with large height. II’, Trans. Amer. Math. Soc. 359 (2007), 427–445.Google Scholar
Mathoverflow, ‘Asymptotics for algebraic numbers of height less than one’, Question 177206 https://mathoverflow.net/questions/177206/.Google Scholar
Mignotte, M., ‘On algebraic integers of small measure’, in: Topics in Classical Number Theory (Budapest, 1981), Colloq. Math. Soc. János Bolyai 34, II (ed. Halász, G.) (North-Holland, Amsterdam, 1984), 1069–1077.Google Scholar
Pomerance, C., ‘Popular values of Euler’s function’, Mathematika 27 (1980), 84–89.Google Scholar
Specht, W., ‘Abschätzungen der Wurzeln algebraischer Gleichungen’, Math. Z. 52 (1949), 310–321.Google Scholar
Waldschmidt, M., Diophantine Approximation on Linear Algebraic Groups. Transcendence Properties of the Exponential Function in Several Variables, Grundlehren der Mathematischen Wissenschaften, 326 (Springer, Berlin, 2000).Google Scholar
Widmer, M., ‘Integral points of fixed degree and bounded height’, Int. Math. Res. Not. IMRN 2016(13) (2016), 3906–3943.Google Scholar