No CrossRef data available.
Article contents
PARTITIONS OF NATURAL NUMBERS AND THEIR WEIGHTED REPRESENTATION FUNCTIONS
Published online by Cambridge University Press: 27 October 2023
Abstract
For any positive integers 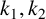 $k_1,k_2$ and any set
$k_1,k_2$ and any set 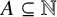 $A\subseteq \mathbb {N}$, let
$A\subseteq \mathbb {N}$, let 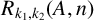 $R_{k_1,k_2}(A,n)$ be the number of solutions of the equation
$R_{k_1,k_2}(A,n)$ be the number of solutions of the equation 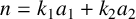 $n=k_1a_1+k_2a_2$ with
$n=k_1a_1+k_2a_2$ with 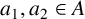 $a_1,a_2\in A$. Let g be a fixed integer. We prove that if
$a_1,a_2\in A$. Let g be a fixed integer. We prove that if 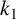 $k_1$ and
$k_1$ and 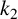 $k_2$ are two integers with
$k_2$ are two integers with 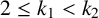 $2\le k_1<k_2$ and
$2\le k_1<k_2$ and 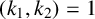 $(k_1,k_2)=1$, then there does not exist any set
$(k_1,k_2)=1$, then there does not exist any set 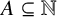 $A\subseteq \mathbb {N}$ such that
$A\subseteq \mathbb {N}$ such that 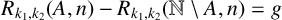 $R_{k_1,k_2}(A,n)-R_{k_1,k_2}(\mathbb {N}\setminus A,n)=g$ for all sufficiently large integers n, and if
$R_{k_1,k_2}(A,n)-R_{k_1,k_2}(\mathbb {N}\setminus A,n)=g$ for all sufficiently large integers n, and if 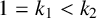 $1=k_1<k_2$, then there exists a set A such that
$1=k_1<k_2$, then there exists a set A such that 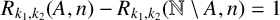 $R_{k_1,k_2}(A,n)-R_{k_1,k_2}(\mathbb {N}\setminus A,n)=1$ for all positive integers n.
$R_{k_1,k_2}(A,n)-R_{k_1,k_2}(\mathbb {N}\setminus A,n)=1$ for all positive integers n.
MSC classification
- Type
- Research Article
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.
Footnotes
This work is supported by the National Natural Science Foundation of China (Grant Nos. 12101009 and 12371005), Anhui Provincial Natural Science Foundation (Grant No. 2108085QA02) and University Natural Science Research Project of Anhui Province (Grant No. 2022AH050171).





