Hostname: page-component-8448b6f56d-m8qmq Total loading time: 0 Render date: 2024-04-23T06:30:43.143Z Has data issue: false hasContentIssue false
  • English
  • Français

THE NUMBER OF ROOTS OF A POLYNOMIAL SYSTEM

Part of: Commutative algebra: Homological methods Graph theory Algebraic combinatorics Extremal combinatorics

Published online by Cambridge University Press:  09 November 2020

NGUYEN CONG MINH Open the ORCID record for NGUYEN CONG MINH [Opens in a new window] ,
LUU BA THANG Open the ORCID record for LUU BA THANG [Opens in a new window]  and
TRAN NAM TRUNG Open the ORCID record for TRAN NAM TRUNG [Opens in a new window]
NGUYEN CONG MINH
Affiliation:
Department of Mathematics, Hanoi National University of Education, 136 Xuan Thuy, Hanoi, Vietnam e-mail: minhnc@hnue.edu.vn
LUU BA THANG*
Affiliation:
Department of Mathematics, Hanoi National University of Education, 136 Xuan Thuy, Hanoi, Vietnam
TRAN NAM TRUNG
Affiliation:
Institute of Mathematics, VAST, 18 Hoang Quoc Viet, Hanoi, Vietnam and TIMAS, Thang Long University, Hanoi, Vietnam e-mail: tntrung@math.ac.vn
*
e-mail: thanglb@hnue.edu.vn
Get access Rights & Permissions [Opens in a new window]

Abstract

Let I be a zero-dimensional ideal in the polynomial ring $K[x_1,\ldots ,x_n]$ over a field K. We give a bound for the number of roots of I in 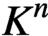$K^n$ counted with combinatorial multiplicity. As a consequence, we give a proof of Alon’s combinatorial Nullstellensatz.

Keywords

combinatorial Nullstellensatzmultiplicitymultisetroot

MSC classification

Primary: 05D40: Probabilistic methods
Secondary: 05C90: Applications 05E40: Combinatorial aspects of commutative algebra 05E45: Combinatorial aspects of simplicial complexes 13D45: Local cohomology
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 103 , Issue 3 , June 2021 , pp. 369 - 378
Check for updates
Copyright
© 2020 Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The third author is partially supported by NAFOSTED (Vietnam), grant number 101.04–2018.307.

References

Alon, N., ‘Combinatorial Nullstellensatz’, Combin. Probab. Comput. 8 (1999), 7–29.10.1017/S0963548398003411CrossRefGoogle Scholar
Alon, N., Nathanson, M. B. and Ruzsa, I. Z., ‘The polynomial method and restricted sums of congruence classes’, J. Number Theory 56 (1996), 404–417.CrossRefGoogle Scholar
Atiyah, M. F. and Macdonald, I. G., Introduction to Commutative Algebra (Addison-Wesley, Reading, MA, 1969).Google Scholar
Cox, D., Little, J. and O’Shea, D., Using Algebraic Geometry (Springer, New York–Berlin–Heidelberg, 1997).Google Scholar
Cox, D., Little, J. and O’Shea, D., Ideals, Varieties, and Algorithms: An Introduction to Computational Algebraic Geometry and Commutative Algebra, 3rd edn (Springer, New York, 2006).Google Scholar
Feng, G.-L., Rao, T. R. N., Berg, G. A. and Zhu, J., ‘Generalized Bezout’s theorem in its applications in coding theory’, IEEE Trans. Inform. Theory 43 (1997), 1799–1810.10.1109/18.641546CrossRefGoogle Scholar
Geil, O. and Høholdt, T., ‘Footprints or generalized Bezout’s theorem’, IEEE Trans. Inform. Theory 46(2) (2000), 635–641.CrossRefGoogle Scholar
Grayson, D. R. and Stillman, M. E., Macaulay2, a Software System for Research in Algebraic Geometry, available at http://www.math.uiuc.edu/Macaulay2/.Google Scholar
Kós, G. and Rónyai, L., ‘Alon’s Nullstellensatz for multisets’, Combinatorica 32(5) (2012), 589–605.10.1007/s00493-012-2758-0CrossRefGoogle Scholar
Lasoń, M., ‘A generalization of combinatorial Nullstellensatz’, Electron. J. Combin. 17(1) (2010), Note 32, 6 pages.CrossRefGoogle Scholar
Tao, T., ‘Algebraic combinatorial geometry: the polynomial method in arithmetic combinatorics, incidence combinatorics, and number theory’, EMS Surv. Math. Sci. 1 (2014), 1–46.10.4171/EMSS/1CrossRefGoogle Scholar