Hostname: page-component-7479d7b7d-rvbq7 Total loading time: 0 Render date: 2024-07-11T08:06:46.089Z Has data issue: false hasContentIssue false
  • English
  • Français

HECKE OPERATORS AND DRINFELD CUSP FORMS OF LEVEL 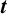$\boldsymbol {t}$

Part of: Special matrices Discontinuous groups and automorphic forms

Published online by Cambridge University Press:  15 June 2022

ANDREA BANDINI Open the ORCID record for ANDREA BANDINI [Opens in a new window]  and
MARIA VALENTINO Open the ORCID record for MARIA VALENTINO [Opens in a new window]
ANDREA BANDINI*
Affiliation:
Dipartimento di Matematica, Università di Pisa, Largo Bruno Pontecorvo 5, Pisa 56127, Italy
MARIA VALENTINO
Affiliation:
Dipartimento di Matematica e Informatica, Università della Calabria, Ponte P. Bucci, Cubo 30B, Rende 87036 (CS), Italy e-mail: maria.valentino@unical.it
*
e-mail: andrea.bandini@unipi.it
Get access Rights & Permissions [Opens in a new window]

Abstract

We use a linear algebra interpretation of the action of Hecke operators on Drinfeld cusp forms to prove that when the dimension of the 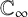$\mathbb {C}_\infty $ -vector space 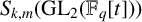$S_{k,m}(\mathrm {{GL}}_2(\mathbb {F}_q[t]))$ is one, the Hecke operator 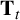$\mathbf {T}_t$ is injective on 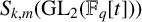$S_{k,m}(\mathrm {{GL}}_2(\mathbb {F}_q[t]))$ and 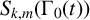$S_{k,m}(\Gamma _0(t))$ is a direct sum of oldforms and newforms.

Keywords

Drinfeld cusp formHecke operatorAtkin–Lehner operatornewformoldform

MSC classification

Primary: 11F52: Modular forms associated to Drinfel'd modules
Secondary: 11F25: Hecke-Petersson operators, differential operators (one variable) 15B99: None of the above, but in this section
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 107 , Issue 2 , April 2023 , pp. 184 - 195
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Atkin, A. O. L. and Lehner, J., ‘Hecke operators on ${\varGamma}_0(\text{m})$ ’, Math. Ann. 185 (1970), 134–160.CrossRefGoogle Scholar
Bandini, A. and Valentino, M., ‘On the Atkin ${U}_t$ -operator for ${\varGamma}_1(t)$ -invariant Drinfeld cusp forms’, Int. J. Number Theory 14 (2018), 2599–2616.CrossRefGoogle Scholar
Bandini, A. and Valentino, M., ‘On the Atkin ${U}_t$ -operator for ${\varGamma}_0(t)$ -invariant Drinfeld cusp forms’, Proc. Amer. Math. Soc. 147 (2019), 4171–4187.CrossRefGoogle Scholar
Bandini, A. and Valentino, M., ‘On the structure and slopes of Drinfeld cusp forms’, Exp. Math., to appear. Published online (25 November 2019).CrossRefGoogle Scholar
Bandini, A. and Valentino, M., ‘On Drinfeld cusp forms of prime level’, Preprint, 2019, arXiv:1908.09768 [math.NT].Google Scholar
Bandini, A. and Valentino, M., ‘Drinfeld cusp forms: oldforms and newforms’, J. Number Theory 237 (2022), 124–144.CrossRefGoogle Scholar
Böckle, G., ‘An Eichler–Shimura isomorphism over function fields between Drinfeld modular forms and cohomology classes of crystals’, available online at https://www1.iwr.uni-heidelberg.de/fileadmin/groups/arithgeo/templates/data/Gebhard_Boeckle/EiShNew.pdf.Google Scholar
Cornelissen, G., ‘A survey of Drinfeld modular forms’, in: Drinfeld Modules, Modular Schemes and Applications (eds. Gekeler, E. U., van der Put, M., Reversat, M. and van Geel, J.) (World Scientific, Singapore, 1997), 167–187.Google Scholar
Dalal, T. and Kumar, N., ‘Notes on Atkin–Lehner theory for Drinfeld modular forms’, Preprint, 2021, arXiv:2112.10340 [math.NT].10.1017/S000497272200123XCrossRefGoogle Scholar
Diamond, F. and Shurman, J., A First Course in Modular Forms, Graduate Texts in Mathematics, 228 (Springer, New York, 2005).Google Scholar
Fresnel, J. and van der Put, M., Géométrie Analytique Rigide et Applications, Progress in Mathematics, 18 (Birkhäuser, Boston, MA, 1981).Google Scholar
Teitelbaum, J. T., ‘The Poisson kernel for Drinfeld modular curves’, J. Amer. Math. Soc. 4(3) (1991), 491–511.CrossRefGoogle Scholar
Valentino, M., ‘Atkin–Lehner theory for Drinfeld modular forms and applications’, Ramanujan J. 58 (2022), 633–649.CrossRefGoogle Scholar