Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Wuthrich, Mario V.
2013.
Non-Life Insurance: Mathematics & Statistics.
SSRN Electronic Journal,
Merz, Michael
and
Wuthrich, Mario V.
2014.
Claims Run-Off Uncertainty: The Full Picture.
SSRN Electronic Journal,
Linde, Marc
2016.
Multi-Year Non-Life Insurance Risk for Correlated Loss Portfolios Under Chain Ladder Model Assumptions.
SSRN Electronic Journal ,
Lindholm, Mathias
Lindskog, Filip
and
Wahl, Felix
2018.
Estimation of Conditional Mean Squared Error of Prediction for Claims Reserving.
SSRN Electronic Journal,
Dahms, René
2018.
CHAIN-LADDER METHOD AND MIDYEAR LOSS RESERVING.
ASTIN Bulletin,
Vol. 48,
Issue. 1,
p.
3.
Gisler, Alois
2019.
THE RESERVE UNCERTAINTIES IN THE CHAIN LADDER MODEL OF MACK REVISITED.
ASTIN Bulletin,
Vol. 49,
Issue. 03,
p.
787.
Wahl, Felix
Lindholm, Mathias
and
Verrall, Richard
2019.
The collective reserving model.
Insurance: Mathematics and Economics,
Vol. 87,
Issue. ,
p.
34.
England, P.D.
Verrall, R.J.
and
Wüthrich, M.V.
2019.
On the lifetime and one-year views of reserve risk, with application to IFRS 17 and Solvency II risk margins.
Insurance: Mathematics and Economics,
Vol. 85,
Issue. ,
p.
74.
Wahl, Felix
2019.
Explicit moments for a class of micro-models in non-life insurance.
Insurance: Mathematics and Economics,
Vol. 89,
Issue. ,
p.
140.
Lindholm, Mathias
Lindskog, Filip
and
Wahl, Felix
2020.
Estimation of conditional mean squared error of prediction for claims reserving.
Annals of Actuarial Science,
Vol. 14,
Issue. 1,
p.
93.
Siegenthaler, Filippo
2020.
The Prediction Uncertainties in the Chain-Ladder Model of Mack: Building on the Latest Gisler Developments.
SSRN Electronic Journal ,
Szatkowski, Marcin
and
Delong, Łukasz
2021.
One-Year and Ultimate Reserve Risk in Mack Chain Ladder Model.
Risks,
Vol. 9,
Issue. 9,
p.
152.
Szatkowski, Marcin
and
Delong, Lukasz
2021.
One-year and ultimate reserve risk in Mack Chain Ladder model.
SSRN Electronic Journal ,
Gisler, Alois
2021.
Estimation error and bootstrapping in the chain-ladder model of Mack.
European Actuarial Journal,
Vol. 11,
Issue. 1,
p.
269.
Siegenthaler, Filippo
2021.
The ultimate prediction uncertainty in the chain-ladder model of Mack: An unbiased estimator.
SSRN Electronic Journal ,
Embrechts, Paul
and
Wüthrich, Mario V.
2022.
Recent Challenges in Actuarial Science.
Annual Review of Statistics and Its Application,
Vol. 9,
Issue. 1,
p.
119.
Siegenthaler, Filippo
2023.
Unbiased estimator for the ultimate claim prediction error in the chain-ladder model of Mack.
Annals of Actuarial Science,
Vol. 17,
Issue. 1,
p.
118.
Zou, Hong
2024.
Esearch on the optimization path of campus football teaching based on deep learning mode.
Applied Mathematics and Nonlinear Sciences,
Vol. 9,
Issue. 1,
Engler, Nils
and
Lindskog, Filip
2024.
Mack’s estimator motivated by large exposure asymptotics in a compound poisson setting.
ASTIN Bulletin,
Vol. 54,
Issue. 2,
p.
310.
Chang, Le
Gao, Guangyuan
and
Shi, Yanlin
2024.
A semi-parametric claims reserving model with monotone splines.
Annals of Operations Research,
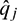 , where ûj measures the (relative) uncertainty around the jth development factor and
, where ûj measures the (relative) uncertainty around the jth development factor and 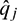 the proportion of the estimated ultimate loss that it affects. The error propagation method also provides a natural split into process error and parameter error. Our proofs identify and exploit symmetries of “chain ladder processes” in a novel way. For the sake of wider practical applicability of the formulae derived, we allow for incomplete historical data and the exclusion of outliers in the triangles.
the proportion of the estimated ultimate loss that it affects. The error propagation method also provides a natural split into process error and parameter error. Our proofs identify and exploit symmetries of “chain ladder processes” in a novel way. For the sake of wider practical applicability of the formulae derived, we allow for incomplete historical data and the exclusion of outliers in the triangles.



