Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Billinge, Simon J. L.
Duxbury, Phillip M.
Gonçalves, Douglas S.
Lavor, Carlile
and
Mucherino, Antonio
2018.
Recent results on assigned and unassigned distance geometry with applications to protein molecules and nanostructures.
Annals of Operations Research,
Vol. 271,
Issue. 1,
p.
161.
Lavor, Carlile
Liberti, Leo
Donald, Bruce
Worley, Bradley
Bardiaux, Benjamin
Malliavin, Thérèse E.
and
Nilges, Michael
2019.
Minimal NMR distance information for rigidity of protein graphs.
Discrete Applied Mathematics,
Vol. 256,
Issue. ,
p.
91.
Camargo, Valter S.
Castelani, Emerson V.
Fernandes, Leandro A. F.
and
Fidalgo, Felipe
2019.
Geometric Algebra to Describe the Exact Discretizable Molecular Distance Geometry Problem for an Arbitrary Dimension.
Advances in Applied Clifford Algebras,
Vol. 29,
Issue. 4,
Alencar, Jorge
Lavor, Carlile
and
Liberti, Leo
2019.
Realizing Euclidean distance matrices by sphere intersection.
Discrete Applied Mathematics,
Vol. 256,
Issue. ,
p.
5.
Guler, Basak
Avestimehr, A. Salman
and
Ortega, Antonio
2019.
Privacy-Aware Distributed Graph-Based Semi-Supervised Learning.
p.
1.
Gonçalves, Douglas S.
Lavor, Carlile
Liberti, Leo
and
Souza, Michael
2021.
A New Algorithm for the $$^K$$DMDGP Subclass of Distance Geometry Problems with Exact Distances.
Algorithmica,
Vol. 83,
Issue. 8,
p.
2400.
Lavor, Carlile
Souza, Michael
Carvalho, Luiz M.
Gonçalves, Douglas S.
and
Mucherino, Antonio
2021.
Improving the sampling process in the interval Branch-and-Prune algorithm for the discretizable molecular distance geometry problem.
Applied Mathematics and Computation,
Vol. 389,
Issue. ,
p.
125586.
Duxbury, Phil
Lavor, Carlile
Liberti, Leo
and
de Salles-Neto, Luiz Leduino
2022.
Unassigned distance geometry and molecular conformation problems.
Journal of Global Optimization,
Vol. 83,
Issue. 1,
p.
73.
Lavor, Carlile
Alves, Rafael
and
Fernandes, Leandro A.F.
2022.
Linear and geometric algebra approaches for sphere and spherical shell intersections in Rn.
Expert Systems with Applications,
Vol. 187,
Issue. ,
p.
115993.
Labiak, Rodrigo
Lavor, Carlile
and
Souza, Michael
2022.
Distance geometry and protein loop modeling.
Journal of Computational Chemistry,
Vol. 43,
Issue. 5,
p.
349.
Ondes, Burla E.
and
Hunter, Susan R.
2023.
An upper bound on the Hausdorff distance between a Pareto set and its discretization in bi-objective convex quadratic optimization.
Optimization Letters,
Vol. 17,
Issue. 1,
p.
45.
Riter, Vinicius
Alves, Rafael
and
Lavor, Carlile
2024.
Advanced Computational Applications of Geometric Algebra.
Vol. 13771,
Issue. ,
p.
88.
Espinoza, Jesús F.
and
Esquer-Pérez, Cynthia G.
2024.
Intersection Properties of Finite Disk Collections.
Mathematics,
Vol. 12,
Issue. 4,
p.
547.
Xu, Chaonong
and
Jiang, Yujie
2024.
Collaborative Computing: Networking, Applications and Worksharing.
Vol. 563,
Issue. ,
p.
173.
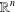 $\mathbb{R}^{n}$
$\mathbb{R}^{n}$ $n$-dimensional spheres in
$n$-dimensional spheres in 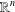 $\mathbb{R}^{n}$ is an interesting problem with applications in trilateration, global positioning systems, multidimensional scaling and distance geometry. In this paper, we generalize some known results on finding the intersection of spheres, based on QR decomposition. Our main result describes the intersection of any number of
$\mathbb{R}^{n}$ is an interesting problem with applications in trilateration, global positioning systems, multidimensional scaling and distance geometry. In this paper, we generalize some known results on finding the intersection of spheres, based on QR decomposition. Our main result describes the intersection of any number of  $n$-dimensional spheres without the assumption that the centres of the spheres are affinely independent. A possible application in the interval distance geometry problem is also briefly discussed.
$n$-dimensional spheres without the assumption that the centres of the spheres are affinely independent. A possible application in the interval distance geometry problem is also briefly discussed.



