1 Introduction
The motivation for our modelling comes from a European Study Group with Industry held in 2017 at the University of Limerick. Electromagnetic measurements made by an automatic microwave analyser during offload of bauxite ore from a ship to an alumina factory were provided to the study group. Signal attenuation data indicated a highly nonlinear dependence on bauxite depth or height h, at odds with the linear calibration used in the microwave analyser to infer moisture content [Reference McGuinness, Bohun, Cregan, Lee, Dewynne, O’Keeffe, Vo, McKibbin, Wake and Saeki23].
The alumina company has a strong interest in accurately measuring moisture content in bauxite ore, because payment for ore is by the tonne and the moisture content has a strong effect on the weight of the ore mix. So it is desirable to reliably and automatically check the moisture content. Spot checks on samples have traditionally been made and are a gold standard approach, being based on changes in mass measured in the lab after driving off the water content of a sample by heating. However, this process is labour-intensive and cannot be undertaken very frequently. Water has a relatively high permittivity for microwaves, so using a low-power microwave analyser to detect moisture content in a way that is nondestructive and almost continuous in time is a promising approach.
The microwave analyser is mounted across a conveyor belt that is transporting bauxite ore from ship to factory, with a square-shaped transmitting antenna close below the belt and an identical receiving antenna approximately 0.6 m above, arranged so that transmitted signals pass through the ore mixture before arriving at the receiving antenna, as sketched in Figure 1. This is termed the free space transmission method, especially when used to determine dielectric properties [Reference Gonçalves, Brancaccio, Ferreira and da Silva8], although our purpose here is rather to measure moisture content.

Figure 1 A sketch of the microwave analyser antennae mounted across a bauxite ore conveyor belt, showing key dimensions. The blue arrows illustrate microwave rays scattering from the rough ore surface, with some being lost to the environment. The ore is travelling into the page. (Colour available online.)
The analyser measures raw electromagnetic microwave signal data, and a separately mounted ultrasound system simultaneously detects the height of bauxite currently on the belt. Measurements are made while the ore is moving on the conveyor belt at 1.8 m s
![]() $^{-1}$
. Movement of the microwaves is to a good approximation one-dimensional and vertical. The ore is at varying heights but typically approximately 250 mm high and is approximately level on the top. However, the top is not smooth and has lumps of ore of varying size there. Once each second, the analyser outputs a moisture content M (wet basis, that is, the mass of water in a sample divided by the total mass of that sample of moist bauxite mixture). The algorithm used by the analyser to infer M is
$^{-1}$
. Movement of the microwaves is to a good approximation one-dimensional and vertical. The ore is at varying heights but typically approximately 250 mm high and is approximately level on the top. However, the top is not smooth and has lumps of ore of varying size there. Once each second, the analyser outputs a moisture content M (wet basis, that is, the mass of water in a sample divided by the total mass of that sample of moist bauxite mixture). The algorithm used by the analyser to infer M is
where the constants
![]() $c_0$
,
$c_0$
,
![]() $c_1$
and
$c_1$
and
![]() $c_2$
are fitted during calibration to the moisture content of laboratory samples,
$c_2$
are fitted during calibration to the moisture content of laboratory samples,
![]() $\Delta \phi $
is the phase shift in radians in the complex valued electric field signal
$\Delta \phi $
is the phase shift in radians in the complex valued electric field signal
![]() $E(h)$
at the receiving antenna when bauxite height is h and L is the signal attenuation, given in dB by
$E(h)$
at the receiving antenna when bauxite height is h and L is the signal attenuation, given in dB by
This form for attenuation is also referred to as the electromagnetic shielding efficiency [Reference Vojtech, Neruda and Hajek37] of the bauxite material. The phase shift (from the phase value of the detected electric field when
![]() $h=0$
) is the argument of the complex number
$h=0$
) is the argument of the complex number
![]() $E(h)/E(0)$
,
$E(h)/E(0)$
,
This is similar to the approach reported by Vianna [Reference Vianna36] for a microwave analyser in an alumina factory in Brazil. They had access to belt tonnage measurements, but they reported more reliable results if they used measurements of material height, thereby assuming (as we do here) constant material porosity.
The raw data measured by the microwave analyser are signal strength (
![]() $-L$
) and two phase shifts. The scales for this data are arbitrary, calibrated when setting up the analyser to be a number in the range [0,1000]. The two phase values, together with ore height values, may be interpreted, as explained by [Reference McGuinness, Bohun, Cregan, Lee, Dewynne, O’Keeffe, Vo, McKibbin, Wake and Saeki23], to obtain the lifted or total phase shift of the microwave signal
$-L$
) and two phase shifts. The scales for this data are arbitrary, calibrated when setting up the analyser to be a number in the range [0,1000]. The two phase values, together with ore height values, may be interpreted, as explained by [Reference McGuinness, Bohun, Cregan, Lee, Dewynne, O’Keeffe, Vo, McKibbin, Wake and Saeki23], to obtain the lifted or total phase shift of the microwave signal
![]() $\Delta \phi $
in radians, zeroed at
$\Delta \phi $
in radians, zeroed at
![]() $h=0$
. One phase shift of the received signal relative to a reference signal is usually computed in electronic equipment by clipping each signal to a square wave with amplitude in the set {0,1}, then taking the average area of the XOR of the waves over some time that is much larger than their period. This provides a number
$h=0$
. One phase shift of the received signal relative to a reference signal is usually computed in electronic equipment by clipping each signal to a square wave with amplitude in the set {0,1}, then taking the average area of the XOR of the waves over some time that is much larger than their period. This provides a number
![]() $\theta $
for the phase difference in the range [0,
$\theta $
for the phase difference in the range [0,
![]() $\pi $
] for a signal expressed using radians as (say)
$\pi $
] for a signal expressed using radians as (say)
![]() $\sin \theta $
. A second phase shift is obtained by shifting the first by approximately
$\sin \theta $
. A second phase shift is obtained by shifting the first by approximately
![]() $\pi /2$
, so that together, they can be used to provide a phase shift in the range [0, 2
$\pi /2$
, so that together, they can be used to provide a phase shift in the range [0, 2
![]() $\pi $
]. The phase shift range can be extended indefinitely [Reference McGuinness, Bohun, Cregan, Lee, Dewynne, O’Keeffe, Vo, McKibbin, Wake and Saeki23] beyond [0, 2
$\pi $
]. The phase shift range can be extended indefinitely [Reference McGuinness, Bohun, Cregan, Lee, Dewynne, O’Keeffe, Vo, McKibbin, Wake and Saeki23] beyond [0, 2
![]() $\pi $
] by also using the height data that are simultaneously collected by an ultrasound system attached to the microwave analyser.
$\pi $
] by also using the height data that are simultaneously collected by an ultrasound system attached to the microwave analyser.
The linear dependence on bauxite height h used in the calibration (1.1) is a poor fit to signal strength data [Reference McGuinness, Bohun, Cregan, Lee, Dewynne, O’Keeffe, Vo, McKibbin, Wake and Saeki23, Reference Paea, Paea and McGuinness25]. A linear behaviour is consistent with semi-infinite models that ignore reflections in ore and air layers, whereas data indicate that attenuation is dominated by the nonlinear interference effects associated with reflections that depend strongly on a variable bauxite ore height h. Hence, the linear regression that is routinely used in automated microwave analysers may fail to accurately infer moisture content from signal strength, when the range of ore heights or ore wetness gives a strongly nonlinear dependence on h.
The four-layer model developed by Paea et al. [Reference Paea, Paea and McGuinness25] provides a better match to nonlinear attenuation data and notes the important effects of signal reflections on that data. There is some exploration of the effects of mixture electromagnetic properties on data. However, there is no consideration in [Reference Paea, Paea and McGuinness25] of how to determine moisture content using the four-layer model.
Our primary motivation here is to use mixture theory to connect moisture content to average electromagnetic properties, especially permittivity and electric conductivity, allowing the use of the four-layer model to predict moisture content from phase shift and attenuation data. This would be considered as an improvement in the usefulness of the four-layer model in the industrial context, where the interest is in inferring moisture content from analyser data. It also improves the accuracy of the model by explicitly allowing for the fact that variations of moisture content affect both permittivity and conductivity, so that these two parameters are not really independent as assumed by Paea et al. [Reference Paea, Paea and McGuinness25].
A concerning result in that paper [Reference Paea, Paea and McGuinness25] is that data are not always invertible when inferring electromagnetic properties, particularly when inferring mixture permittivity solely from strength data. This raises an important question as to whether the same issue of noninvertibility applies to inferring moisture content from data when using the four-layer model. So while our primary motivation in linking moisture to electromagnetic properties is to be useful to users of the microwave analyser, such a link will allow us also to answer the question: is it mathematically possible to infer moisture content from data according to the mathematical model solution?
A second motivation and point of difference for the present work is that we seek to improve the four-layer model by extending it to allow for the effects of scattering at the rough upper surface of the bauxite ore.
We summarise in Section 2 the four-layer model and solution of Paea et al. [Reference Paea, Paea and McGuinness25], then in Section 3, we review the existing relationships between ore electromagnetic properties, and its porosity and moisture content, which allow us to provide preliminary results on the use of a microwave analyser for inferring moisture content of bauxite ore in real time.
In Section 4, we extend the four-layer model to allow for the effects of scattering in the region above the bauxite. Our extended model is solved to provide an explicit forward formula for the received signal when microwaves pass through bauxite ore and scatter in the air space above it. This formula depends on the operating frequency of the microwaves, antenna properties, the amount of scattering above the bauxite, the permittivity of solid ore, the porosity of the mined ore mixture, the electrical conductivity of the liquid in the pores and the moisture content of the ore. The extended model is compared in Section 5 with our previous model, and the invertibility of our extended model is explored, together with its dependence on the key parameters of the bauxite and microwave system. Conclusions follow in Section 6.
2 Four-layer mathematical model
We begin with a description of the model published by Paea et al. [Reference Paea, Paea and McGuinness25], which provides good fits to analyser data. The four layers or regions in our conceptual and mathematical model (a layer of bauxite ore sandwiched between two air layers, with a conducting antenna or receiver on the top) are sketched in Figure 2 together with directions of travel for the plane wave solutions, approximated at this stage as being in the vertical dimension. We do not explicitly model the transmitting antenna.

Figure 2 A sketch of the four-layer model, showing origin, and the distances D and h in the x-direction. Arrows indicate directions of travel for the plane electromagnetic waves.
The origin of the model is fixed at the surface of the empty conveyor belt. The variable nonnegative bauxite height is denoted h, while the receiving antenna is fixed at
![]() $x = D>h$
. The wave arriving at the base of the bauxite from the transmitting antenna is taken to be a free space wave travelling in the positive x-direction, with axes oriented so that the electric field has z-component
$x = D>h$
. The wave arriving at the base of the bauxite from the transmitting antenna is taken to be a free space wave travelling in the positive x-direction, with axes oriented so that the electric field has z-component
![]() $E(x) e^{-i \omega t}$
and the magnetic field has y-component
$E(x) e^{-i \omega t}$
and the magnetic field has y-component
![]() $H(x) e^{-i \omega t}$
. The angular frequency is
$H(x) e^{-i \omega t}$
. The angular frequency is
![]() $\omega =2 \pi f$
and the operating frequency f is listed in Table 1 for the data we use. It is a consequence of Maxwell’s equations that electric fields
$\omega =2 \pi f$
and the operating frequency f is listed in Table 1 for the data we use. It is a consequence of Maxwell’s equations that electric fields
![]() $E(x)$
in all layers then satisfy the wave equation, which is a linear differential equation,
$E(x)$
in all layers then satisfy the wave equation, which is a linear differential equation,
 $$ \begin{align} \frac{\partial ^2 E}{\partial x^2} =-\mu \omega^2 \epsilon E -i\mu\omega \sigma E , \end{align} $$
$$ \begin{align} \frac{\partial ^2 E}{\partial x^2} =-\mu \omega^2 \epsilon E -i\mu\omega \sigma E , \end{align} $$
where
![]() $i^2=-1$
. The permittivity
$i^2=-1$
. The permittivity
![]() $\epsilon $
and the electrical conductivity
$\epsilon $
and the electrical conductivity
![]() $\sigma $
take different values in different layers, while the permeability is taken to be that of free space
$\sigma $
take different values in different layers, while the permeability is taken to be that of free space
![]() $\mu = \mu _0$
in all four layers, since bauxite ore is usually considered to be nonmagnetic [Reference Paea, Paea and McGuinness25]. Parameter values used later, unless noted otherwise, are listed in Table 1.
$\mu = \mu _0$
in all four layers, since bauxite ore is usually considered to be nonmagnetic [Reference Paea, Paea and McGuinness25]. Parameter values used later, unless noted otherwise, are listed in Table 1.
Table 1 Model parameters and default values used in four-layer model simulations.

Without loss of generality, we take permittivity
![]() $\epsilon $
and conductivity
$\epsilon $
and conductivity
![]() $\sigma $
to be real quantities. The permittivity is
$\sigma $
to be real quantities. The permittivity is
![]() $\epsilon = \epsilon _r \epsilon _0$
, where relative permittivities
$\epsilon = \epsilon _r \epsilon _0$
, where relative permittivities
![]() $\epsilon _r$
take the value one in air and antenna. The relative permittivity of the bauxite ore mixture depends strongly on moisture content, because water has a high value of relative permittivity compared with dry solid bauxite. Electrical conductivity
$\epsilon _r$
take the value one in air and antenna. The relative permittivity of the bauxite ore mixture depends strongly on moisture content, because water has a high value of relative permittivity compared with dry solid bauxite. Electrical conductivity
![]() $\sigma $
is zero in air and negligible in solid bauxite, and is high in the receiving antenna. It is also an important property in the bauxite mixture that varies with moisture content, because pore water is expected to contain significant dissolved salts.
$\sigma $
is zero in air and negligible in solid bauxite, and is high in the receiving antenna. It is also an important property in the bauxite mixture that varies with moisture content, because pore water is expected to contain significant dissolved salts.
The substitution of
![]() $E = e^{ikx}$
into (2.1) gives a quadratic for wavenumber k,
$E = e^{ikx}$
into (2.1) gives a quadratic for wavenumber k,
where the dissipation
![]() ${\cal D} = \sigma /(\omega \epsilon )$
is the magnitude of the conduction current density divided by the magnitude of the displacement current density [Reference Lorrain, Corson and Lorrain22], and is zero in air. Then there are two solutions
${\cal D} = \sigma /(\omega \epsilon )$
is the magnitude of the conduction current density divided by the magnitude of the displacement current density [Reference Lorrain, Corson and Lorrain22], and is zero in air. Then there are two solutions
![]() $\pm k$
, complex-valued in bauxite and in the receiving antenna, but real-valued in air:
$\pm k$
, complex-valued in bauxite and in the receiving antenna, but real-valued in air:
The real part of k may be written in the form [Reference Lorrain, Corson and Lorrain22, 11.3.1]
 $$\begin{align*}\Re (k) = \omega \sqrt{ \frac{\epsilon \mu }{2}} ( \sqrt{1 + {\cal D}^2} + 1)^{1/2} ,\end{align*}$$
$$\begin{align*}\Re (k) = \omega \sqrt{ \frac{\epsilon \mu }{2}} ( \sqrt{1 + {\cal D}^2} + 1)^{1/2} ,\end{align*}$$
while the imaginary part of k may be written in the form
 $$\begin{align*}\Im (k) = \omega \sqrt{ \frac{\epsilon \mu }{2}} ( \sqrt{1 + {\cal D}^2} - 1 )^{1/2}. \end{align*}$$
$$\begin{align*}\Im (k) = \omega \sqrt{ \frac{\epsilon \mu }{2}} ( \sqrt{1 + {\cal D}^2} - 1 )^{1/2}. \end{align*}$$
The real part of k gives the wavelength
![]() $\lambda = 2 \pi / \Re (k) $
of electric field oscillations. The imaginary part gives growth or decay rates of the amplitudes of these oscillations as x increases.
$\lambda = 2 \pi / \Re (k) $
of electric field oscillations. The imaginary part gives growth or decay rates of the amplitudes of these oscillations as x increases.
2.1 Model solutions
The solutions to the differential equations in each layer take the general form
Each part of the solution (2.3), when considered together with the time dependence
![]() $e^{-i \omega t}$
, corresponds to a wave that travels in the positive or negative x-direction, respectively. We seek the solution at the surface
$e^{-i \omega t}$
, corresponds to a wave that travels in the positive or negative x-direction, respectively. We seek the solution at the surface
![]() $x=D$
of the receiving antenna, the upward-travelling wave
$x=D$
of the receiving antenna, the upward-travelling wave
Solving our coupled system of differential equations is possible, determining at the same time all reflection and transmission coefficients, thanks to the boundary conditions that arise from requiring continuity of electric and magnetic fields tangential at each interface in the model. The details are given in detail in [Reference Paea, Paea and McGuinness25] and are summarised in Appendix A for completeness. The solution is
 $$ \begin{align} E_a = E_{4+} = \frac{ 8 Z_0^2 Z_A Z_b \; e^{ik(D-h)} e^{ik_b h}}{F} , \end{align} $$
$$ \begin{align} E_a = E_{4+} = \frac{ 8 Z_0^2 Z_A Z_b \; e^{ik(D-h)} e^{ik_b h}}{F} , \end{align} $$
where
 $$ \begin{align*} F &= (Z_b^2 - Z_0^2)(Z_0-Z_A) ( e^{2ik_b h} - 1 ) e^{2ik(D-h)} \nonumber \\ & \quad + [ (Z_0-Z_b)^2 e^{2i k_b h} - (Z_0+Z_b)^2 ](Z_0 + Z_A) , \end{align*} $$
$$ \begin{align*} F &= (Z_b^2 - Z_0^2)(Z_0-Z_A) ( e^{2ik_b h} - 1 ) e^{2ik(D-h)} \nonumber \\ & \quad + [ (Z_0-Z_b)^2 e^{2i k_b h} - (Z_0+Z_b)^2 ](Z_0 + Z_A) , \end{align*} $$
and the impedance of material with subscript
![]() $i= 0, A, b$
(free space, antenna and bauxite ore) is
$i= 0, A, b$
(free space, antenna and bauxite ore) is
![]() $Z_i = \mu _i \omega / k_i $
. Elsewhere, the subscript b indicates properties of the bauxite ore mixture and the subscript A indicates effective properties in the receiving antenna region. The symbol k with no subscript is used for the wavenumber in air, where the dissipation
$Z_i = \mu _i \omega / k_i $
. Elsewhere, the subscript b indicates properties of the bauxite ore mixture and the subscript A indicates effective properties in the receiving antenna region. The symbol k with no subscript is used for the wavenumber in air, where the dissipation
![]() ${\cal D}$
is zero and k is real.
${\cal D}$
is zero and k is real.
Equation (2.4) looks complicated, but the exponential terms indicate the major dependence on
![]() $k(D-h)$
, due to the air layer in Region 3 of thickness
$k(D-h)$
, due to the air layer in Region 3 of thickness
![]() $D-h$
with no attenuation, and on
$D-h$
with no attenuation, and on
![]() $k_b h$
, due to the bauxite layer in Region 2 of thickness h with some attenuation. In particular, the wavelengths of the resulting received signal can be seen to be determined by the sums and differences of the real part of
$k_b h$
, due to the bauxite layer in Region 2 of thickness h with some attenuation. In particular, the wavelengths of the resulting received signal can be seen to be determined by the sums and differences of the real part of
![]() $k_b$
and k. Bauxite mixture properties affect the values of
$k_b$
and k. Bauxite mixture properties affect the values of
![]() $\epsilon _b$
and
$\epsilon _b$
and
![]() $\sigma _b$
, which directly affect
$\sigma _b$
, which directly affect
![]() $k_b$
and
$k_b$
and
![]() $Z_b$
according to (A.1).
$Z_b$
according to (A.1).
Previous work [Reference Paea, Paea and McGuinness25] has shown that the four-layer solution (2.4) has behaviour that is a good match to attenuation data obtained from an alumina manufacturer in Ireland. A typical set of matches of our model solution to attenuation and phase data is presented here in Figure 3 for two different values for the effective relative permittivity
![]() $\epsilon _r$
of the bauxite mixture. In particular, the wavelengths associated with reflections and interference in the air gap Region 3 above the bauxite, and the shorter wavelengths arising from reflections within the bauxite ore, are apparent in the attenuation data and, to a lesser extent, in the phase shift data.
$\epsilon _r$
of the bauxite mixture. In particular, the wavelengths associated with reflections and interference in the air gap Region 3 above the bauxite, and the shorter wavelengths arising from reflections within the bauxite ore, are apparent in the attenuation data and, to a lesser extent, in the phase shift data.

Figure 3 Model solutions (lines) compared with data (dot symbols) obtained with a microwave analyser. The data are signal strength and phase shift
![]() $\Delta \phi $
(radians) at the receiving antenna, plotted against ore height h. Signal strength data have been linearly scaled to provide a visual match to the model results, which are in dB. The relative permittivities of the bauxite ore mixture used for the two model solutions are listed in the legend. Sag is set to zero here. Other parameter values are listed in Table 1.
$\Delta \phi $
(radians) at the receiving antenna, plotted against ore height h. Signal strength data have been linearly scaled to provide a visual match to the model results, which are in dB. The relative permittivities of the bauxite ore mixture used for the two model solutions are listed in the legend. Sag is set to zero here. Other parameter values are listed in Table 1.
3 Moisture in ore
The outstanding question is the one originally posed by the alumina manufacturer at the European Study Group with Industry at the University of Limerick in 2017, that is, how to use the microwave analyser data to accurately infer moisture content in the bauxite ore. The four-layer model [Reference Paea, Paea and McGuinness25] provides good matches to analyser data and explains what is causing the oscillations seen especially in attenuation, but it only allows to infer electromagnetic properties of the ore mixture and stops short of using data to infer the moisture content of the ore.
We briefly review theories of how the relative amounts of components of a mixture of solid bauxite, air and water affect the measured average or effective values of permittivity and conductivity of the bulk mixture. We adopt soil and porous medium conventions for describing the mixture. The ore is considered to be a solid with porosity n, and the pore space is occupied by air and water. The term solid is used to refer to all of the components in the mix that are not air or liquid water, irrespective of their state. The liquid saturation S is the volume fraction of pore space occupied by liquid water. Air then occupies the remaining volume fraction
![]() $1-S$
of pore space. Saturation ranges from zero to one in value and, together with porosity and densities, determines the water fraction by weight. Solid ore occupies the volume fraction
$1-S$
of pore space. Saturation ranges from zero to one in value and, together with porosity and densities, determines the water fraction by weight. Solid ore occupies the volume fraction
![]() $(1-n)$
. We seek averaged or effective properties of the ore as a conducting dielectric mixture, when high-frequency EM waves pass through at frequencies above 100 MHz.
$(1-n)$
. We seek averaged or effective properties of the ore as a conducting dielectric mixture, when high-frequency EM waves pass through at frequencies above 100 MHz.
The relative permittivity of the solid matrix that characterises the dry bauxite parent matrix is variable and is sensitive to clay content, but it remains much less that the value for water. Schön [Reference Schön28, Section 8.7.2] lists values for smectite, kaolin, illite and quartz in the range
![]() $4 \le \epsilon _{rb} \le 10$
, with lower values for frequencies near 1 GHz. Anecdotally, there are four different types of bauxite shipped into the factory near Limerick, which may have four different values for solid permittivity. The water content is known to have a strong influence on the mixture permittivity
$4 \le \epsilon _{rb} \le 10$
, with lower values for frequencies near 1 GHz. Anecdotally, there are four different types of bauxite shipped into the factory near Limerick, which may have four different values for solid permittivity. The water content is known to have a strong influence on the mixture permittivity
![]() $\epsilon _r$
. The solid permittivity is an unknown parameter that needs to be determined by calibration or directly measured before using a microwave analyser to infer moisture content.
$\epsilon _r$
. The solid permittivity is an unknown parameter that needs to be determined by calibration or directly measured before using a microwave analyser to infer moisture content.
The moisture content M as a mass fraction on a wet basis is the mass of water in a given mass of mixture,
with parameter values given in Table 1. Rearranging this definition gives the saturation S as a function of M for given n and density values,
 $$ \begin{align} S = \frac{M[ (1-n) \rho_s + n \rho_a]}{n [ \rho_w (1-M) + \rho_a] }. \end{align} $$
$$ \begin{align} S = \frac{M[ (1-n) \rho_s + n \rho_a]}{n [ \rho_w (1-M) + \rho_a] }. \end{align} $$
A plot of saturation S versus moisture content M over the moisture range [0.04,0.14] will be nearly linear since
![]() $1-M \approx 1$
. The plots in Figure 4 for porosity
$1-M \approx 1$
. The plots in Figure 4 for porosity
![]() $n=0.5$
illustrate how linear
$n=0.5$
illustrate how linear
![]() $S(M)$
is, as well as the typical ranges of S resulting from the usual ranges of moisture content seen in bauxite ore shipments.
$S(M)$
is, as well as the typical ranges of S resulting from the usual ranges of moisture content seen in bauxite ore shipments.

Figure 4 Liquid water saturation S as a function of water content M (mass %, wet basis) (symbols). The straight solid line joins the first and last data points to illustrate linearity. Parameter values used are as listed in Table 1.
The laboratory measurements that are used in the bauxite industry to independently measure water content and then to calibrate the microwave analyser are based on weights measured before and after heating the bauxite samples in an oven. Heating to 100
![]() $^\circ $
C may not drive off tightly bound water [Reference Wang, Lu, Ren and Lu39]. Heating to 200
$^\circ $
C may not drive off tightly bound water [Reference Wang, Lu, Ren and Lu39]. Heating to 200
![]() $^\circ $
C is usually enough to drive off most of the bound water. Bound water content can be up to 4% by weight if organic matter is not present, depending on the specific surface area of the soil (especially the clay content); typically, approximately 20% of bound water is tightly bound.
$^\circ $
C is usually enough to drive off most of the bound water. Bound water content can be up to 4% by weight if organic matter is not present, depending on the specific surface area of the soil (especially the clay content); typically, approximately 20% of bound water is tightly bound.
Connolly et al. [Reference Connolly, Josh, O’Neill, Seltzer, Wigand, Clennell, May and Johns6] note that at frequencies above 10 MHz, the dielectric permittivity of reservoir rocks containing water and oil relates primarily to the volume fractions of constituent minerals and saturation, and is not sensitive to the distinction between bound and free water. At low frequencies below 10 MHz, bound water is associated with interfacial polarisation, electro-diffusion and ohmic conduction, which have an affect on measurements. Hence, for our purposes, the distinction between bound and free water is not relevant as the frequencies under consideration are above 10 MHz.
The mining and loading process means that an approximation of the bauxite ore mixture as a random mixture of solid, air and liquid is likely a good one. The bauxite offloaded from a ship has been mined from natural rock formations which, before mining, have a wide range of porosities. It contains a range of particle sizes and looks like lumpy soil. It typically consists of a reddish clay material, containing hydrated alumina with variable proportions of iron oxides, silica and titanium dioxide. The space available to be filled with water inside the bauxite is the porosity n, a volume fraction. Porosity takes values ranging from 0.41 to 0.67 for loams and sands [Reference Reynolds, Bowman, Drury, Tan and Lu27]. Polydisperse sands [Reference Nimmo and Hillel24] have
![]() $n \in [0.30,0.35]$
. Guelph silt loam [Reference Smith, Smettem, Broadbridge and Woolhiser33] has
$n \in [0.30,0.35]$
. Guelph silt loam [Reference Smith, Smettem, Broadbridge and Woolhiser33] has
![]() $n \in [0.4,0.5]$
. Bulk density of bauxite is typically 1400–1500 kg m
$n \in [0.4,0.5]$
. Bulk density of bauxite is typically 1400–1500 kg m
![]() $^{-3}$
. If rock density is 2800 kg m
$^{-3}$
. If rock density is 2800 kg m
![]() $^{-3}$
, this implies a porosity of value 0.5.
$^{-3}$
, this implies a porosity of value 0.5.
We will use the notation
for relative permittivities of mixture, bauxite solids, air and water, respectively.
3.1 Mixture permittivity
Reviews of studies of the macroscopic dielectric properties in the geophysical and physics contexts include [Reference Chelidze and Gueguen3, Reference Landauer, Garland and Tanner21, Reference Sihvola31, Reference Sihvola32, Reference Stroud34]. Early work on how the properties of mixtures depend on the properties of constituents goes right back to Maxwell in 1864 and the Clausius–Mossotti relation [Reference Lorrain, Corson and Lorrain22, Section 3.8] for the effective relative permittivity
![]() $\epsilon _r$
when there are
$\epsilon _r$
when there are
![]() $N_j$
molecules of species j present in a unit volume of free space, each with polarisability
$N_j$
molecules of species j present in a unit volume of free space, each with polarisability
![]() $\alpha _j$
:
$\alpha _j$
:
 $$ \begin{align*} \frac{\epsilon_r-1}{\epsilon_r+2} = \frac{1}{3\epsilon_0}\sum_jN_j\alpha_j. \end{align*} $$
$$ \begin{align*} \frac{\epsilon_r-1}{\epsilon_r+2} = \frac{1}{3\epsilon_0}\sum_jN_j\alpha_j. \end{align*} $$
L.V. Lorenz and H.A. Lorentz obtained a similar formula for refractive index [Reference Sihvola31, Ch. 1].
In 1892, Lord Rayleigh used the Clausius–Mossotti relation to calculate the Rayleigh mixing formula for the effective relative permittivity
![]() $\epsilon _r$
of a mixture with spherical or cylindrical inclusions ordered in a rectangular matrix. It generalises for K different types of inclusion in free space to [Reference Sihvola31, Section 4.1]
$\epsilon _r$
of a mixture with spherical or cylindrical inclusions ordered in a rectangular matrix. It generalises for K different types of inclusion in free space to [Reference Sihvola31, Section 4.1]
 $$ \begin{align} \frac{\epsilon_r - 1}{\epsilon_r + 2} = \sum _{j=1} ^K f_j \bigg( \frac{\epsilon_j - 1}{\epsilon_j + 2}\bigg), \end{align} $$
$$ \begin{align} \frac{\epsilon_r - 1}{\epsilon_r + 2} = \sum _{j=1} ^K f_j \bigg( \frac{\epsilon_j - 1}{\epsilon_j + 2}\bigg), \end{align} $$
where
![]() $f_j$
is the volume fraction occupied by the jth type of inclusion which has relative permittivity
$f_j$
is the volume fraction occupied by the jth type of inclusion which has relative permittivity
![]() $\epsilon _j$
.
$\epsilon _j$
.
The Rayleigh mixing formula is also known as the Maxwell–Garnett mixing rule [Reference Sihvola31, Reference Sihvola32] and is related to work by Wagner in 1924 [Reference Chelidze and Gueguen3], when made explicit in the effective permittivity.
This early work was derived in the limit of very dilute mixtures and was found to give poor matches to experimental measurements. A response with good matches to data has been termed the Maxwell–Wagner–Bruggeman–Hanai (MWBH) theory of effective media [Reference Bruggeman2, Reference Chen and Or5, Reference Hanai, Koizumi and Gotoh12]. Bruggeman developed new theories which do not require dilute mixtures, which take account of bulk properties, shape and volume fractions of components. The MWBH theory has been found to correctly predict both the permittivity and the conductivity for porous water-bearing rocks at frequencies greater than 10 MHz [Reference Chelidze and Gueguen3, Reference Chelidze, Gueguen and Ruffet4]. At lower frequencies, surface effects associated with bound water can render the MWBH theory ineffective in matching experimental data. The frequencies in which we are interested allow us to use the MWBH theory, which depends on bulk or total water content.
Bruggeman developed two major formulae, one symmetric and one nonsymmetric, for a single inclusion in a parent material. In terms of a parent material that is solid bauxite, with water included via a saturated porosity n, Bruggeman’s symmetric mixing formula is
The effective relative permittivity
![]() $\epsilon _r$
of the mixture is given implicitly by (3.3). The same result can be derived using a self-consistency argument in the effective medium approach [Reference Apresyan, Rasmagin, Krasovskiy, Kryshtob and Kazaryan1, Reference Kolesnikov, Yakovlev, Bardushkin, Lavrov, Sychev and Yakovlev19, Reference Landauer20, Reference Stroud34].
$\epsilon _r$
of the mixture is given implicitly by (3.3). The same result can be derived using a self-consistency argument in the effective medium approach [Reference Apresyan, Rasmagin, Krasovskiy, Kryshtob and Kazaryan1, Reference Kolesnikov, Yakovlev, Bardushkin, Lavrov, Sychev and Yakovlev19, Reference Landauer20, Reference Stroud34].
The symmetric formula (3.3) can be written as a quadratic in the permittivity
![]() $\epsilon _r$
of the averaged medium. The correct root may be chosen by noting that there are bounds on its value, corresponding to parallel and series circuits [Reference Jansson and Arwin16], also termed Weiner’s upper and lower bounds [Reference Jansson and Arwin16]. Alternatively, the correct root follows by ensuring one chooses the root with the correct limiting values as n goes to zero or one. A simple approach is to express n as a function of
$\epsilon _r$
of the averaged medium. The correct root may be chosen by noting that there are bounds on its value, corresponding to parallel and series circuits [Reference Jansson and Arwin16], also termed Weiner’s upper and lower bounds [Reference Jansson and Arwin16]. Alternatively, the correct root follows by ensuring one chooses the root with the correct limiting values as n goes to zero or one. A simple approach is to express n as a function of
![]() $\epsilon _r$
, then switch x- and y-axes. Porosity does not have to be small in (3.3). Relatively modern derivations of Bruggeman’s symmetric equation (3.3) use effective medium approximations [Reference Apresyan, Rasmagin, Krasovskiy, Kryshtob and Kazaryan1, Reference Kolesnikov, Yakovlev, Bardushkin, Lavrov, Sychev and Yakovlev19, Reference Stroud34].
$\epsilon _r$
, then switch x- and y-axes. Porosity does not have to be small in (3.3). Relatively modern derivations of Bruggeman’s symmetric equation (3.3) use effective medium approximations [Reference Apresyan, Rasmagin, Krasovskiy, Kryshtob and Kazaryan1, Reference Kolesnikov, Yakovlev, Bardushkin, Lavrov, Sychev and Yakovlev19, Reference Stroud34].
Using his symmetric form, Bruggeman developed and solved a differential equation, obtaining a nonsymmetric form for permittivity as a function of volume fraction of contaminant,
 $$ \begin{align} \bigg( \frac{\epsilon_{rw }- \epsilon_r}{\epsilon_{rw}- \epsilon_{rb}} \bigg) \bigg( \frac{\epsilon_{rb}}{\epsilon_r }\bigg)^{1/3} = 1 - n. \end{align} $$
$$ \begin{align} \bigg( \frac{\epsilon_{rw }- \epsilon_r}{\epsilon_{rw}- \epsilon_{rb}} \bigg) \bigg( \frac{\epsilon_{rb}}{\epsilon_r }\bigg)^{1/3} = 1 - n. \end{align} $$
Some authors [Reference Chelidze and Gueguen3, Reference Chen and Or5] refer to this nonsymmetric Bruggeman solution (3.4) as the MWBH solution. Hanai [Reference Hanai and Sherman11] showed that both Bruggeman formulae can be generalised to electrical conductivities or complex-valued permittivities. Hanai et al. [Reference Hanai10, Reference Hanai, Koizumi and Gotoh12, Reference Hanai, Koizumi, Sugamo and Gotoh13] find that the nonsymmetric Bruggeman solution (3.4) is a good match to measurements of dielectric permittivity, and of electrical conductivity in water and oil emulsions.
Comparisons of Bruggeman’s nonsymmetric formula (3.4) and symmetric formula (3.3) with data from saturated sandstone in Figure 5 suggest that both formulae give reasonable matches.

Figure 5 Comparisons of measured permittivity in saturated sandstones (symbols) with Bruggeman’s nonsymmetric formula (3.4) (the MWBH formula, dashed line) and his symmetric mixing formula (3.3) (solid line). Measured data are at frequency 0.5 GHz in saturated tight gas sandstones [Reference De Waal, Nooteboome and Poley7]. A dry bauxite permittivity
![]() $\epsilon _b=7$
has been used for the theoretical formulae.
$\epsilon _b=7$
has been used for the theoretical formulae.
Pecharroman and Iglesias [Reference Pecharromán and Iglesias26] note that Landauer [Reference Landauer20] has also obtained Bruggeman’s symmetric formula, which is easily extended to cases with more than one inclusion [Reference Landauer, Garland and Tanner21]. It seems that Landauer was at first unaware of Bruggeman’s results [Reference Halperin and Bergman9] from 1935.
The Bruggeman nonsymmetric formula is for a single inclusion (water) in solid bauxite. A very interesting extension to this model, which allows for two inclusions (water and air) in solid bauxite, is provided by Jayannavar and Kumar [Reference Jayannavar and Kumar17]. They begin with Bruggeman’s symmetric mixing formula (3.3) which becomes the following for our mixture of solid bauxite, air and water:
where
![]() $\epsilon _r$
is the effective relative permittivity of the mixture. They point out that the unsymmetrical Bruggeman formula is more appropriate to physical situations like saturated porous media, where the background solid phase is not on an equal footing with the filling phase. The symmetrical formula is more suited to ideal binary systems where the two phases should be treated on an equal basis. In seeking a unified treatment of the symmetrical and unsymmetrical formulae, Jayannavar and Kumar use a renormalisation procedure very much like Bruggeman’s derivation that provides an effective medium for a ternary system, like our present case of a solid bauxite porous medium with porosity occupied by air and water. They find a unified solution for the effective relative permittivity
$\epsilon _r$
is the effective relative permittivity of the mixture. They point out that the unsymmetrical Bruggeman formula is more appropriate to physical situations like saturated porous media, where the background solid phase is not on an equal footing with the filling phase. The symmetrical formula is more suited to ideal binary systems where the two phases should be treated on an equal basis. In seeking a unified treatment of the symmetrical and unsymmetrical formulae, Jayannavar and Kumar use a renormalisation procedure very much like Bruggeman’s derivation that provides an effective medium for a ternary system, like our present case of a solid bauxite porous medium with porosity occupied by air and water. They find a unified solution for the effective relative permittivity
![]() $\epsilon _r$
of the mixture that is given in our notation by
$\epsilon _r$
of the mixture that is given in our notation by
 $$ \begin{align} \bigg| \frac{\epsilon_+ - \epsilon_r}{\epsilon_+ - \epsilon_{rb}} \bigg| ^B \bigg| \frac{\epsilon_- - \epsilon_r}{\epsilon_- - \epsilon_{rb}} \bigg|^C \bigg( \frac{\epsilon_{rb}}{\epsilon_r } \bigg)^{1/3} = 1 - n , \end{align} $$
$$ \begin{align} \bigg| \frac{\epsilon_+ - \epsilon_r}{\epsilon_+ - \epsilon_{rb}} \bigg| ^B \bigg| \frac{\epsilon_- - \epsilon_r}{\epsilon_- - \epsilon_{rb}} \bigg|^C \bigg( \frac{\epsilon_{rb}}{\epsilon_r } \bigg)^{1/3} = 1 - n , \end{align} $$
where
 $$ \begin{align} \begin{split} B & = \frac{(\epsilon_{rw} + 2 \epsilon_+)(\epsilon_{ra} + 2 \epsilon_+)}{6 \epsilon_+(\epsilon_+ - \epsilon_-)} , \\ C & = \frac{(\epsilon_{rw} + 2 \epsilon_-)(\epsilon_{ra} + 2 \epsilon_-)}{6 \epsilon_-(\epsilon_- - \epsilon_+)} , \end{split} \end{align} $$
$$ \begin{align} \begin{split} B & = \frac{(\epsilon_{rw} + 2 \epsilon_+)(\epsilon_{ra} + 2 \epsilon_+)}{6 \epsilon_+(\epsilon_+ - \epsilon_-)} , \\ C & = \frac{(\epsilon_{rw} + 2 \epsilon_-)(\epsilon_{ra} + 2 \epsilon_-)}{6 \epsilon_-(\epsilon_- - \epsilon_+)} , \end{split} \end{align} $$
and
![]() $\epsilon _{\pm }$
are the roots of the quadratic in
$\epsilon _{\pm }$
are the roots of the quadratic in
![]() $\epsilon $
,
$\epsilon $
,
The power of 1/3 follows from inserting the air permittivity value
![]() $\epsilon _{ra}=1$
. This specialises (3.5) to apply to relative permittivity; using absolute permittivities is also possible using the same formula.
$\epsilon _{ra}=1$
. This specialises (3.5) to apply to relative permittivity; using absolute permittivities is also possible using the same formula.
The unified solution (3.5) of Jayannavar and Kumar extends Bruggeman’s nonsymmetric solution to the case to two inclusions, and implicitly gives the relative permittivity of a mixture of bauxite, liquid water and air, where solid bauxite has porosity n and the liquid saturation is S in the pores. This provides the connection we need between porosity, saturation and permittivity of bauxite ore. It is symmetrical with respect to interchanging air and water.
As Jayannavar and Kumar point out, their solution provides a unification of Bruggeman’s very successful formulae, symmetrical and nonsymmetrical. If we let
![]() $S \to 0$
or
$S \to 0$
or
![]() $S \to 1$
, then we find that
$S \to 1$
, then we find that
![]() $C \to 0$
and
$C \to 0$
and
![]() $B \to 1$
, and the original MWBH (nonsymmetrical) formula for one contaminant (air or water, respectively) is recovered. If we set the permittivity of air to match that for water, we also recover the MWBH nonsymmetrical formula. However, if we set porosity to one, we recover the symmetrical Bruggeman formula for air and water in free space (because then,
$B \to 1$
, and the original MWBH (nonsymmetrical) formula for one contaminant (air or water, respectively) is recovered. If we set the permittivity of air to match that for water, we also recover the MWBH nonsymmetrical formula. However, if we set porosity to one, we recover the symmetrical Bruggeman formula for air and water in free space (because then,
![]() $\epsilon _r = \epsilon _+$
or
$\epsilon _r = \epsilon _+$
or
![]() $\epsilon _r = \epsilon _-$
and the quadratic (3.7) is the symmetrical formula).
$\epsilon _r = \epsilon _-$
and the quadratic (3.7) is the symmetrical formula).
The permittivities in the above may be absolute permittivity or relative permittivity. When real permittivities are used, as in our development, there are always two different real roots of the quadratic (3.7).
Then given bauxite porosity n and the moisture content by mass fraction M, (3.1) gives liquid volume saturation S, and (3.7) gives the quadratic whose roots
![]() $\epsilon _{\pm }$
are needed. The roots can be found numerically or by using the quadratic formula. Then the terms B and C in (3.6) can be calculated, and (3.5) can be solved implicitly to find the relative permittivity
$\epsilon _{\pm }$
are needed. The roots can be found numerically or by using the quadratic formula. Then the terms B and C in (3.6) can be calculated, and (3.5) can be solved implicitly to find the relative permittivity
![]() $\epsilon _r$
of the mixture of bauxite, water and air. This provides for our model the connection between water content and the permittivity of the bauxite mixture.
$\epsilon _r$
of the mixture of bauxite, water and air. This provides for our model the connection between water content and the permittivity of the bauxite mixture.
The Jayannavar and Kumar unified solution has a critical value of saturation
![]() $S=S_c$
at which
$S=S_c$
at which
![]() $\epsilon _+ = \epsilon _{rb}$
. Then the solution (3.5) is undefined, and the correct solution is that the effective relative permittivity of the mixture is constant and is equal to
$\epsilon _+ = \epsilon _{rb}$
. Then the solution (3.5) is undefined, and the correct solution is that the effective relative permittivity of the mixture is constant and is equal to
![]() $\epsilon _{rb}$
, independent of n. This is because at this value of saturation, the combination of water and air that is being added or subtracted as n varies has the same permittivity as the parent bauxite, so changing the porosity has no effect on permittivity.
$\epsilon _{rb}$
, independent of n. This is because at this value of saturation, the combination of water and air that is being added or subtracted as n varies has the same permittivity as the parent bauxite, so changing the porosity has no effect on permittivity.
One way to solve (3.5) explicitly is to make porosity n the subject, giving n explicitly in terms of
![]() $\epsilon _r$
and S. Then switch axes to obtain
$\epsilon _r$
and S. Then switch axes to obtain
![]() $\epsilon _r$
versus n at a given value of S, as illustrated in Figure 6 for
$\epsilon _r$
versus n at a given value of S, as illustrated in Figure 6 for
![]() $S=1$
.
$S=1$
.

Figure 6 Solutions (3.5) obtained by calculating porosity n for given average relative permittivity of a mixture of bauxite, water and air, then switching abscissa and ordinate axes to get permittivity as a function of n. In panel (a), each curve is for a different value of saturation S as shown in the legend. Each curve doubles back at
![]() $n=1$
and is multiple-valued, requiring care when the inverse function is sought. In panel (b), the saturated case
$n=1$
and is multiple-valued, requiring care when the inverse function is sought. In panel (b), the saturated case
![]() $S=1$
(solid line) is compared with saturated sandstone data [Reference De Waal, Nooteboome and Poley7] (symbols). The solid matrix relative permittivity has been set to 8.5 in both plots. (Colour available online.)
$S=1$
(solid line) is compared with saturated sandstone data [Reference De Waal, Nooteboome and Poley7] (symbols). The solid matrix relative permittivity has been set to 8.5 in both plots. (Colour available online.)
For a given S, there are typically two branches of the solution formula (3.5) seen, joined at
![]() $n=1$
, when trying
$n=1$
, when trying
![]() $\epsilon _r$
in the range [1,
$\epsilon _r$
in the range [1,
![]() $\epsilon _{rw}$
]. This is illustrated in Figure 6, where mixture relative permittivity
$\epsilon _{rw}$
]. This is illustrated in Figure 6, where mixture relative permittivity
![]() $\epsilon _r$
is plotted against porosity n for several fixed values of saturation S and with solid bauxite relative permittivity set to
$\epsilon _r$
is plotted against porosity n for several fixed values of saturation S and with solid bauxite relative permittivity set to
![]() $\epsilon _{rb}=8.5$
for illustration purposes. It is important to choose the branch that comes out of the correct initial value
$\epsilon _{rb}=8.5$
for illustration purposes. It is important to choose the branch that comes out of the correct initial value
![]() $\epsilon _r(0)= \epsilon _{rb} =8.5$
, before doubling back at
$\epsilon _r(0)= \epsilon _{rb} =8.5$
, before doubling back at
![]() $n=1$
. For saturations above critical, this is the lower branch; for saturations below critical, the correct branch is the upper one, in a plot of
$n=1$
. For saturations above critical, this is the lower branch; for saturations below critical, the correct branch is the upper one, in a plot of
![]() $\epsilon _r(n)$
.
$\epsilon _r(n)$
.
We are interested in the effect of adding water to, or removing it from, bauxite, with a given fixed porosity. This means changing the saturation S for fixed n. Note that the branches join at
![]() $n=1$
, that is, when
$n=1$
, that is, when
![]() $\epsilon _r = \epsilon _+$
, which is when
$\epsilon _r = \epsilon _+$
, which is when
where a, b and c are the coefficients in the quadratic (3.7) for
![]() $\epsilon $
expressed in the popular form
$\epsilon $
expressed in the popular form
![]() $a \epsilon ^2 + b \epsilon + c =0$
, and
$a \epsilon ^2 + b \epsilon + c =0$
, and
Note that the correct solution branches all have
![]() $\epsilon _r$
values that lie between dry bauxite
$\epsilon _r$
values that lie between dry bauxite
![]() $\epsilon _{rb}$
and the fully saturated solutions
$\epsilon _{rb}$
and the fully saturated solutions
![]() $\epsilon _r = \epsilon _+$
. Hence, we ensure we are on the correct branch when solving implicitly, by restricting the search for the value of
$\epsilon _r = \epsilon _+$
. Hence, we ensure we are on the correct branch when solving implicitly, by restricting the search for the value of
![]() $\epsilon _r$
, given S, as follows:
$\epsilon _r$
, given S, as follows:
-
(a) if
 $S<S_c$
, the correct branch lies in
$S<S_c$
, the correct branch lies in
 $[\epsilon _+,\epsilon _{rb}]$
;
$[\epsilon _+,\epsilon _{rb}]$
; -
(b) if
 $S=S_c$
, the solution is
$S=S_c$
, the solution is
 $\epsilon _r = \epsilon _{rb}$
;
$\epsilon _r = \epsilon _{rb}$
; -
(c) if
 $S>S_c$
, the correct branch lies in
$S>S_c$
, the correct branch lies in
 $[\epsilon _{rb},\epsilon _+]$
.
$[\epsilon _{rb},\epsilon _+]$
.
The resulting values of mixture relative permittivity
![]() $\epsilon _r$
are plotted against liquid water saturation for
$\epsilon _r$
are plotted against liquid water saturation for
![]() $n \in [0.3,0.6]$
in Figure 7, after setting
$n \in [0.3,0.6]$
in Figure 7, after setting
![]() $\epsilon _{rb} = 8.5$
for illustration purposes. Note the curves all pass through the critical value
$\epsilon _{rb} = 8.5$
for illustration purposes. Note the curves all pass through the critical value
![]() $S_c \approx 0.361$
, where mixture permittivity matches dry bauxite permittivity.
$S_c \approx 0.361$
, where mixture permittivity matches dry bauxite permittivity.

Figure 7 Solutions to (3.5) obtained by using an implicit equation solver (fzero in Matlab) on restricted ranges of mixture permittivity. Mixture permittivity is plotted against liquid water saturation, for porosity values
![]() $n =$
0.3, 0.4, 0.5, 0.6 as in the legend. Dry bauxite relative permittivity has been set to 8.5. (Colour available online.)
$n =$
0.3, 0.4, 0.5, 0.6 as in the legend. Dry bauxite relative permittivity has been set to 8.5. (Colour available online.)
A plot of inferred mixture relative permittivity, as a function of moisture content that is given by (3.5), is presented in Figure 8 for various porosity values and using dry bauxite permittivity
![]() $\epsilon _{rb} = 8.5$
. Equation (3.1) is used to convert from moisture content M to saturation. We use (3.5) and (3.1) to connect bauxite mixture permittivity to moisture content in the remainder of this paper.
$\epsilon _{rb} = 8.5$
. Equation (3.1) is used to convert from moisture content M to saturation. We use (3.5) and (3.1) to connect bauxite mixture permittivity to moisture content in the remainder of this paper.

Figure 8 Mixture relative permittivity as a function of water content M (mass %, wet basis). Relative permittivity calculated using the extended nonsymmetric Bruggeman solution (3.5), with saturation given as the function (3.1) of water content M. Density values used are listed in Table 1. Porosity is set to 0.4 in panel (a) and to values in the range [0.3, 0.6] as indicated in the legend in panel (b). Solid dry bauxite relative permittivity has been set to 8.5 in all plots for illustration purposes. (Colour available online.)
3.2 Bauxite conductivity
The Bruggeman approach outlined above may, in principle, be used to also calculate mixture conductivity. Equation (3.5) cannot be directly translated from permittivities to conductivities as, for example, the power of 1/3 is directly due to air having a relative permittivity of one. Using the Rayleigh mixing formula (3.2) or Bruggeman’s symmetric formula (3.3) leads to a mixture conductivity that is linear in moisture content, whereas experiments indicate that a quadratic power law (Archie’s law) is a more accurate fit [Reference Hunt, Ewing and Ghanbarian14, Reference Hunt15].
Measured values of conductivity for soils depend strongly on the clay component, partly because finer soils retain more moisture. Values for sands are
![]() $\sigma \in [0.1,2]$
mS m
$\sigma \in [0.1,2]$
mS m
![]() $^{-1}$
, for silts
$^{-1}$
, for silts
![]() $\sigma \in [2,20]$
mS m
$\sigma \in [2,20]$
mS m
![]() $^{-1}$
and for clays
$^{-1}$
and for clays
![]() $\sigma \in [10,1000]$
mS m
$\sigma \in [10,1000]$
mS m
![]() $^{-1}$
[Reference Serrano, Shahidian and Marques da Silva30]. Other measurements of dry and wet soils [Reference Serrano, Shahidian and Marques da Silva29, Reference Serrano, Shahidian and Marques da Silva30] give electrical conductivity values in the range of 10–100 mS m
$^{-1}$
[Reference Serrano, Shahidian and Marques da Silva30]. Other measurements of dry and wet soils [Reference Serrano, Shahidian and Marques da Silva29, Reference Serrano, Shahidian and Marques da Silva30] give electrical conductivity values in the range of 10–100 mS m
![]() $^{-1}$
.
$^{-1}$
.
The electrical conductivity of air is zero and we expect that the electrical conductivity of perfectly dry solid bauxite is negligible, since feldspars have
![]() $\sigma \approx 10^{-11}$
S m
$\sigma \approx 10^{-11}$
S m
![]() $^{-1}$
, and clays have
$^{-1}$
, and clays have
![]() $\sigma \approx 10^{-7} $
S m
$\sigma \approx 10^{-7} $
S m
![]() $^{-1}$
[Reference Knight and Butler18]. Hence, our case is similar to that of a single conductor (brine) in free space. A simpler derivation of the equivalent to Bruggeman’s nonsymmetric formula is then possible. Landauer [Reference Landauer, Garland and Tanner21], for example, finds that starting with pure conductor and removing portions of it, renormalising in the same spirit as Bruggeman, Archie’s law can be derived giving the mixture conductivity as
$^{-1}$
[Reference Knight and Butler18]. Hence, our case is similar to that of a single conductor (brine) in free space. A simpler derivation of the equivalent to Bruggeman’s nonsymmetric formula is then possible. Landauer [Reference Landauer, Garland and Tanner21], for example, finds that starting with pure conductor and removing portions of it, renormalising in the same spirit as Bruggeman, Archie’s law can be derived giving the mixture conductivity as
with
![]() $\sigma $
equal to the pure conductor value
$\sigma $
equal to the pure conductor value
![]() $\sigma _0$
, when the volume fraction of pure conductor is
$\sigma _0$
, when the volume fraction of pure conductor is
![]() $\theta =1$
.
$\theta =1$
.
Hunt et al. [Reference Hunt, Ewing and Ghanbarian14] find that electrical conductivity is better modelled for porous media in three dimensions by Archie’s empirical law with power two, giving
where
![]() $\theta = n S$
is moisture content as a volume fraction and
$\theta = n S$
is moisture content as a volume fraction and
![]() $\sigma _w$
is related to the conductivity of the water in the pores. Hence, in this simple percolation model,
$\sigma _w$
is related to the conductivity of the water in the pores. Hence, in this simple percolation model,
![]() $\sigma $
starts at zero for completely dry bauxite and then increases with an increasing amount of water in pores. The behaviour (3.8) is a good match to numerous experiments on partially saturated soils [Reference Hunt, Ewing and Ghanbarian14, Reference Hunt15], so this is the model we will use here.
$\sigma $
starts at zero for completely dry bauxite and then increases with an increasing amount of water in pores. The behaviour (3.8) is a good match to numerous experiments on partially saturated soils [Reference Hunt, Ewing and Ghanbarian14, Reference Hunt15], so this is the model we will use here.
The pore water is in contact with salts in the solid bauxite and is also vulnerable to seawater entry during shipment to a factory. It is likely to contain ions, which can strongly increase its electrical conductivity. Seawater has surface conductivities
![]() $\sigma _w$
that range from 2.5 to 5 S m
$\sigma _w$
that range from 2.5 to 5 S m
![]() $^{-1}$
[Reference Tyler, Boyer, Minami, Zweng and Reagan35]. This provides an order of magnitude guide to the upper limit we might expect for
$^{-1}$
[Reference Tyler, Boyer, Minami, Zweng and Reagan35]. This provides an order of magnitude guide to the upper limit we might expect for
![]() $\sigma _w$
. Calibrating our four-layer model to data from the Maia shipment of bauxite, where
$\sigma _w$
. Calibrating our four-layer model to data from the Maia shipment of bauxite, where
![]() $\sigma = 40$
mS m
$\sigma = 40$
mS m
![]() $^{-1}$
and lab moisture measurements are approximately
$^{-1}$
and lab moisture measurements are approximately
![]() $M=$
10%, so that
$M=$
10%, so that
![]() $S=0.5$
and
$S=0.5$
and
![]() $\theta \approx 0.2$
, suggests that the pore water in the ore has
$\theta \approx 0.2$
, suggests that the pore water in the ore has
The resulting dependence of electrical conductivity for wet bauxite of porosity 0.4 on moisture content M is plotted in Figure 9.
3.3 Preliminary results
We now use in our four-layer model solution (2.4) the dependences of mixture permittivity and conductivity on moisture content summarised in (3.5) and (3.8), together with the relationship (3.1) between saturation S and moisture content M.
The four-layer model solution (2.4) then depends on a number of parameters that need to be determined by calibrating against data. They are
![]() $D_0$
(distance from empty belt to receiving antenna), ore porosity n, water conductivity
$D_0$
(distance from empty belt to receiving antenna), ore porosity n, water conductivity
![]() $\sigma _w$
, solid ore relative permittivity
$\sigma _w$
, solid ore relative permittivity
![]() $\epsilon _{rb}$
and the main quantity that we are interested in determining from analyser data, moisture content M (mass fraction, wet basis). There is also a small dependence on belt sag.
$\epsilon _{rb}$
and the main quantity that we are interested in determining from analyser data, moisture content M (mass fraction, wet basis). There is also a small dependence on belt sag.
Values that are used in the following sections (unless otherwise stated) are listed together with posited antenna values in Table 1. Salty pore water has almost the same relative permittivity as pure water, so we use
![]() $\epsilon _{rw} = 80$
. The data used for comparison in the figures to follow have been obtained using a microwave analyser during offload of ore from the ship Maia.
$\epsilon _{rw} = 80$
. The data used for comparison in the figures to follow have been obtained using a microwave analyser during offload of ore from the ship Maia.
Attempts to fit the four-layer solution to signal strength data and phase shift data (plotted versus ore height h) indicate strong sensitivity to parameter values and highly correlated effects. When using the existing model, it is difficult to obtain solution plots that are everywhere reasonably close to signal strength data behaviour. This difficulty is illustrated in Figure 10, which has been obtained after a hand-search for the best values of the parameters
![]() $D_0$
, n,
$D_0$
, n,
![]() $\sigma _w$
and
$\sigma _w$
and
![]() $\epsilon _{rb}$
, and also guided by indicative values from technical drawings and existing literature on soil properties.
$\epsilon _{rb}$
, and also guided by indicative values from technical drawings and existing literature on soil properties.

Figure 10 Four-layer model solutions (lines) compared with data (dot symbols) for various moisture content values. The data are signal strength SS (dB) and phase shift
![]() $\Delta \phi $
(radians) at the receiving antenna. The moisture contents used in the model are given in the legend. Other parameter values are listed in Table 1. There is no scattering or sag allowed for in this model. (Colour available online.)
$\Delta \phi $
(radians) at the receiving antenna. The moisture contents used in the model are given in the legend. Other parameter values are listed in Table 1. There is no scattering or sag allowed for in this model. (Colour available online.)
Some of the plots in Figure 10 provide a reasonable match to small h signal strength data, while others give better matches to larger h data points. While the four-layer model is promising in capturing many aspects of the large and small oscillations present in data, it fails to provide a single set of parameter values giving a reasonably good match (especially to signal strength data) over the entire height range. Hence, we seek to improve our four-layer model. We do this by considering the effects of scattering off the rough surface of the ore and the effects of belt sag.
Note that the model results for signal strength in Figure 10 indicate a problem with nonuniqueness. There are places where the model is not invertible. That is, a unique value of moisture content cannot be found from the signal strength data, in some ranges of ore height, as evidenced by the crossing-over of model solution curves.
The model results for phase shift do not suffer from this problem; they are nonlinear, but are invertible giving a unique moisture content for a data point
![]() $(h, \Delta \phi )$
.
$(h, \Delta \phi )$
.
4 Extended four-layer model
Before further investigation of the four-layer model’s sensitivity to parameter values, we extend the model by allowing for the effects of scattering in a simple way. Scattering is inherently a two- or three-dimensional phenomenon, with waves incident on the rough upper surface of the ore being scattered in various directions. One consequence is that some of the waves escape to free space without again meeting the receiving antenna, reducing the received signal strength.
The surface of the bauxite ore has been modelled as a level smooth surface that is normal to the direction of microwave travel. This has allowed the use of a model that has a single spatial dimension. In reality, the surface of the ore is lumpy and a little curved, with lump sizes ranging from 12 to 30 mm in diameter. The wavelength in air of our microwaves is approximately 330 mm. This puts the scattering from lumps at this interface in the upper region of the Rayleigh scattering regime where the wavelength is much greater than the roughness length-scale [Reference Voronovich38].
The effect of the roughness is to scatter microwaves, as they exit the bauxite ore into Region 3 in Figure 2 and as they reflect back upwards from the ore surface after going downwards towards it. There is an entire field of mathematical physics devoted to the study of scattering at interfaces, for example, [Reference Voronovich38].
The effect of the scattering is to dissipate some of the microwave power out to the environment, undetected by the receiving antenna. Scattering is properly captured by going to a model that is fully three-dimensional, but we seek to imitate some of the consequences of scattering by modifying our four-layer model, by adding attenuation in Region 3, while retaining the simplicity of a one-dimensional model (in space).
The transmitting and receiving antennae are squares with sides
![]() $L\approx 0.5$
m, as illustrated in the sketch in Figure 1. The distance from the surface of the ore to the receiving antenna is
$L\approx 0.5$
m, as illustrated in the sketch in Figure 1. The distance from the surface of the ore to the receiving antenna is
![]() $D-h$
. This distance varies, from approximately
$D-h$
. This distance varies, from approximately
![]() $L=0.5$
m when the belt is empty to approximately 0.2 m when the belt is fully loaded. The solid angle fraction subtended by the receiving antenna on the shadow of the transmitting antenna at the ore surface varies from order one when this distance is near zero to a value that varies approximately linearly with
$L=0.5$
m when the belt is empty to approximately 0.2 m when the belt is fully loaded. The solid angle fraction subtended by the receiving antenna on the shadow of the transmitting antenna at the ore surface varies from order one when this distance is near zero to a value that varies approximately linearly with
![]() $D-h$
, increasing as
$D-h$
, increasing as
![]() $D-h$
increases.
$D-h$
increases.
A simple over-estimate of an upper limit on losses due to scattering in Region 3 is based on assuming a uniform distribution of energy – the area
![]() $L^2$
of the receiving antenna divided by the total area
$L^2$
of the receiving antenna divided by the total area
![]() $L^2 + 4L (D-h)$
of the virtual box of height
$L^2 + 4L (D-h)$
of the virtual box of height
![]() $D-h$
covering the bauxite provides an estimate of received signal strength
$D-h$
covering the bauxite provides an estimate of received signal strength
![]() $SF$
as a fraction of total signal,
$SF$
as a fraction of total signal,
 $$\begin{align*}SF \approx \frac{L^2}{L^2 + 4L (D-h)}. \end{align*}$$
$$\begin{align*}SF \approx \frac{L^2}{L^2 + 4L (D-h)}. \end{align*}$$
Here,
![]() $SF$
varies from one when
$SF$
varies from one when
![]() $D-h$
is zero to 1/3 when
$D-h$
is zero to 1/3 when
![]() $D-h$
reaches its maximum value
$D-h$
reaches its maximum value
![]() $L/2$
.
$L/2$
.
We simulate the loss of signal by introducing a decay term through the value of k in Region 3. Previously, k was the real value valid for propagation through air. We will modify k to
![]() $k_3 = k + i k_s$
in Region 3, where
$k_3 = k + i k_s$
in Region 3, where
![]() $k = \omega \sqrt {\epsilon _0 \mu _0} = \omega /c$
is the real value in free space. The value
$k = \omega \sqrt {\epsilon _0 \mu _0} = \omega /c$
is the real value in free space. The value
![]() $k_s$
of the imaginary part of
$k_s$
of the imaginary part of
![]() $k_3$
due to scattering will be hand-fitted to get a better model fit to signal strength data. An estimate for
$k_3$
due to scattering will be hand-fitted to get a better model fit to signal strength data. An estimate for
![]() $k_s$
is found by requiring the damping term
$k_s$
is found by requiring the damping term
![]() $e^{-k_s (D-h)}$
to equal the upper estimate value of 1/3 when
$e^{-k_s (D-h)}$
to equal the upper estimate value of 1/3 when
![]() $D-h$
is
$D-h$
is
![]() $L/2$
, so that
$L/2$
, so that
Then using
![]() $L = 0.5$
m, our upper estimate is
$L = 0.5$
m, our upper estimate is
![]() $ k_s \approx 4 \; \mathrm {m}^{-1}$
. In practice, we find a suitable value for
$ k_s \approx 4 \; \mathrm {m}^{-1}$
. In practice, we find a suitable value for
![]() $k_s \approx 1.5$
m
$k_s \approx 1.5$
m
![]() $^{-1}$
by matching to data and we generally expect scattering losses to be represented by a number that is much less than four.
$^{-1}$
by matching to data and we generally expect scattering losses to be represented by a number that is much less than four.
4.1 Scattering above ore
We seek to modify the four-layer model, to allow the wavenumber
![]() $k_3$
in Region 3 in Figure 2 to be different to k in free space to imitate one effect of scattering at the surface of the bauxite ore by allowing decaying wave amplitudes in the direction of travel in this region. The augmented matrix (A.8) in Appendix A that summarises the continuity conditions at the three interfaces is then modified to
$k_3$
in Region 3 in Figure 2 to be different to k in free space to imitate one effect of scattering at the surface of the bauxite ore by allowing decaying wave amplitudes in the direction of travel in this region. The augmented matrix (A.8) in Appendix A that summarises the continuity conditions at the three interfaces is then modified to
 $$ \begin{align*} \left( \begin{array}{cccccc|c} 1, & 1, & -Z_0, & 0, & 0, & 0 & -Z_0\\ 1, & -1, & Z_b, & 0, & 0, & 0 & -Z_b\\ e^{i k_b h} , & -e^{-i k_b h} , & 0,& Z_b e^{i k_3 h} , & Z_b e^{-i k_3 h} , & 0& 0\\ e^{i k_b h} , & e^{-i k_b h} , & 0,& Z_3 e^{i k_3 h} , & -Z_3 e^{-i k_3 h} , & 0& 0\\ 0,&0,&0,&Z_a e^{i k_3 D} , & Z_a e^{-i k_3 D}, & 1 & 0\\ 0,&0,&0,&Z_3 e^{i k_3 D} , & -Z_3 e^{-i k_3 D}, & 1 & 0 \end{array} \right ), \end{align*} $$
$$ \begin{align*} \left( \begin{array}{cccccc|c} 1, & 1, & -Z_0, & 0, & 0, & 0 & -Z_0\\ 1, & -1, & Z_b, & 0, & 0, & 0 & -Z_b\\ e^{i k_b h} , & -e^{-i k_b h} , & 0,& Z_b e^{i k_3 h} , & Z_b e^{-i k_3 h} , & 0& 0\\ e^{i k_b h} , & e^{-i k_b h} , & 0,& Z_3 e^{i k_3 h} , & -Z_3 e^{-i k_3 h} , & 0& 0\\ 0,&0,&0,&Z_a e^{i k_3 D} , & Z_a e^{-i k_3 D}, & 1 & 0\\ 0,&0,&0,&Z_3 e^{i k_3 D} , & -Z_3 e^{-i k_3 D}, & 1 & 0 \end{array} \right ), \end{align*} $$
where
![]() $Z_3 = \mu _0 \omega / k_3$
is the new impedance of Region 3. A series of row reductions leads to an upper triangular augmented matrix that allows to solve for the unknowns,
$Z_3 = \mu _0 \omega / k_3$
is the new impedance of Region 3. A series of row reductions leads to an upper triangular augmented matrix that allows to solve for the unknowns,
 $$ \begin{align*} \small \left(\begin{array}{cccccc|c} 1, & 0, & (Z_b-Z_0)/2, & 0, & 0, & 0 & -(Z_0+Z_b)/2\\ 0, & 1, & -(Z_b+Z_0)/2, & 0, & 0, & 0 & (Z_b-Z_0)/2\\[.2cm] 0 , & 0 , & (Z_b + Z_0)e^{-ik_bh},& (Z_0-Z_b) e^{i k h} , & -(Z_0+Z_b) e^{-i k h} , & 0& (Z_0-Z_b)e^{-ik_bh}\\[.2cm] 0 , & 0 , & 0,& A_s e^{ik_3 h} , & B_s e^{-i k_3 h} , & 0& C \\[.2cm] 0,&0,&0,&0 , & 2Z_3 Z_a e^{-i k_3 D}, & Z_3-Z_a & 0\\ 0,&0,&0,&0 , & 0 , & F_s & -2C Z_3 Z_a \end{array}\right), \end{align*} $$
$$ \begin{align*} \small \left(\begin{array}{cccccc|c} 1, & 0, & (Z_b-Z_0)/2, & 0, & 0, & 0 & -(Z_0+Z_b)/2\\ 0, & 1, & -(Z_b+Z_0)/2, & 0, & 0, & 0 & (Z_b-Z_0)/2\\[.2cm] 0 , & 0 , & (Z_b + Z_0)e^{-ik_bh},& (Z_0-Z_b) e^{i k h} , & -(Z_0+Z_b) e^{-i k h} , & 0& (Z_0-Z_b)e^{-ik_bh}\\[.2cm] 0 , & 0 , & 0,& A_s e^{ik_3 h} , & B_s e^{-i k_3 h} , & 0& C \\[.2cm] 0,&0,&0,&0 , & 2Z_3 Z_a e^{-i k_3 D}, & Z_3-Z_a & 0\\ 0,&0,&0,&0 , & 0 , & F_s & -2C Z_3 Z_a \end{array}\right), \end{align*} $$
where
The solution at the receiving antenna with scattering included is given by the last row,
This can be written in the form
where
and the Fresnel coefficients for each region are
Attenuation and phase shift are relative to zero bauxite height values, so we consider the ratio of
![]() $E_{4+}^s(h)$
to
$E_{4+}^s(h)$
to
![]() $E_{4+}^s(0)$
, which can be written in the form
$E_{4+}^s(0)$
, which can be written in the form
 $$ \begin{align} \frac{E_{4+}^s(h)}{E_{4+}^s (0)} = \frac{(R_1 + R_2)R_3 e^{i k_3D} + (R_1 R_2 + 1)e^{-i k_3D}} {(R_1 e^{i k_b h} + R_2 e^{-i k_b h})R_3 e^{i k_3(D-h)} + (R_1 R_2 e^{i k_b h} + e^{-i k_b h})e^{-i k_3(D-h)}}. \end{align} $$
$$ \begin{align} \frac{E_{4+}^s(h)}{E_{4+}^s (0)} = \frac{(R_1 + R_2)R_3 e^{i k_3D} + (R_1 R_2 + 1)e^{-i k_3D}} {(R_1 e^{i k_b h} + R_2 e^{-i k_b h})R_3 e^{i k_3(D-h)} + (R_1 R_2 e^{i k_b h} + e^{-i k_b h})e^{-i k_3(D-h)}}. \end{align} $$
This equation reduces to (2.4) if
![]() $k_3$
is replaced by the free space value k and
$k_3$
is replaced by the free space value k and
![]() $Z_3$
is replaced by
$Z_3$
is replaced by
![]() $Z_0$
.
$Z_0$
.
Equation (4.1) provides the signal detected at the receiving antenna, normalised on the signal received when no bauxite ore is present. It has a complicated-looking appearance, but consists of terms that are independent of bauxite height h, and terms that depend on bauxite height h through exponentials of
![]() $i k_3 h$
and
$i k_3 h$
and
![]() $i k_b h$
. These exponentials are multiplied in the denominator of (4.1) to produce exponentials that depend on sums and differences
$i k_b h$
. These exponentials are multiplied in the denominator of (4.1) to produce exponentials that depend on sums and differences
![]() $i (k_3 + k_b) h$
and
$i (k_3 + k_b) h$
and
![]() $i (k_3 - k_b) h$
. The real parts of
$i (k_3 - k_b) h$
. The real parts of
![]() $k_3+k_b$
and
$k_3+k_b$
and
![]() $k_3 - k_b$
provide wave numbers that give wavelengths for the oscillations described by (4.1). The imaginary parts provide oscillation amplitudes that decay in the direction of wave motion.
$k_3 - k_b$
provide wave numbers that give wavelengths for the oscillations described by (4.1). The imaginary parts provide oscillation amplitudes that decay in the direction of wave motion.
Evaluating
![]() $k_3 $
and
$k_3 $
and
![]() $k_b$
using (3.5), (3.8) and (3.1), together with the parameter values listed in Table 1, gives the approximate values,
$k_b$
using (3.5), (3.8) and (3.1), together with the parameter values listed in Table 1, gives the approximate values,
and for the Fresnel coefficients,
The real parts of the sums and differences are
The resulting wavelengths (
![]() $2 \pi /k$
) for oscillations due to sums and differences of the k are 90 mm and 200 mm. The signal strength according to the four-layer model is
$2 \pi /k$
) for oscillations due to sums and differences of the k are 90 mm and 200 mm. The signal strength according to the four-layer model is
 $$ \begin{align*} SS = 20 \log _{10} \bigg| \frac{E_{4+}^s(h)}{E_{4+}^s (0)} \bigg|. \end{align*} $$
$$ \begin{align*} SS = 20 \log _{10} \bigg| \frac{E_{4+}^s(h)}{E_{4+}^s (0)} \bigg|. \end{align*} $$
Taking the absolute value of a signal that is oscillating about the origin leads to a halving of the apparent wavelength, so that these model results would be consistent with oscillations in signal strength with apparent wavelengths 45 mm and 100 mm. This is broadly in agreement with the signal strength data and model solutions plotted in Figures 10 and 13.
The same wavelengths are visible to a lesser extent in the oscillations in phase shift data and model solutions in Figures 10 and 13. The overall behaviour of the model solution phase shifts is linear in h because it is determined by the term involving the exponential of
![]() $i (k_3-k_b) h$
. This term has a modulus that remains larger than the other terms in the denominator of equation (4.1) as h increases, so that adding the other terms modifies it but does not prevent it from winding up in an approximately linear fashion, to reach a total of ten radians phase shift when h is approximately 0.3 m. This total phase shift is seen in the data and is obtained from the model using the parameter values listed in Table 1.
$i (k_3-k_b) h$
. This term has a modulus that remains larger than the other terms in the denominator of equation (4.1) as h increases, so that adding the other terms modifies it but does not prevent it from winding up in an approximately linear fashion, to reach a total of ten radians phase shift when h is approximately 0.3 m. This total phase shift is seen in the data and is obtained from the model using the parameter values listed in Table 1.
5 Full results
We now present results from our extended four-layer model, which allows for losses due to scattering of reflected signal off the top of the bauxite ore, and for belt sag. We compare the accuracy of our extension that allows for scattering effects with our previous model which did not allow for scattering. We also investigate the invertibility of data when trying to obtain moisture content from data and we explore the model’s sensitivity to parameter values.
5.1 Comparison with previous model
In a previous paper [Reference Paea, Paea and McGuinness25], there was no scattering in Region 3 of Figure 2. We reproduce that model here by fixing our scattering parameter
![]() $k_s=0$
. We compare that previous model with our extended model, by allowing Matlab to automatically minimise the sum of squared residuals between the measured data for signal strength and phase shift and our model results. Allowed ranges and starting values for the parameters that were searched upon are listed in Table 2. For the extended model with scattering, we set the range
$k_s=0$
. We compare that previous model with our extended model, by allowing Matlab to automatically minimise the sum of squared residuals between the measured data for signal strength and phase shift and our model results. Allowed ranges and starting values for the parameters that were searched upon are listed in Table 2. For the extended model with scattering, we set the range
![]() $k_s \in [0,4]$
m
$k_s \in [0,4]$
m
![]() $^{-1}$
with initial value
$^{-1}$
with initial value
![]() $k_s = 1.3$
, which found the value
$k_s = 1.3$
, which found the value
![]() $k_s = 0.73$
m
$k_s = 0.73$
m
![]() $^{-1}$
. For the previous model with no scattering, we set the range
$^{-1}$
. For the previous model with no scattering, we set the range
![]() $k_s \in [0,0]$
. Our extended model with scattering did obtain a fit with a smaller sum of squared residuals (2190) than the previous model (2290), although the extended model did not reach a satisfactory minimum value for the sum of squared residuals during the optimization process.
$k_s \in [0,0]$
. Our extended model with scattering did obtain a fit with a smaller sum of squared residuals (2190) than the previous model (2290), although the extended model did not reach a satisfactory minimum value for the sum of squared residuals during the optimization process.
The resulting fits for the extended model with scattering and for the previous model without scattering are shown in Figures 11 and 12. The extension to approximate the effect of scattering has resulted in a slightly improved fit to the data, as evidenced by the slight reduction in the sum of squares, and by the graphical evidence in Figures 11 and 12 that some of the finer features of the data are better captured by our extended model. The fitted parameters are not much different between the two models. Automated fitting does not provide very convincing fits to the data at typical loading heights near 240 mm, where most of the data are. The curves go nicely through this data region, but do not reproduce very successfully the variation with ore height nearby.
Table 2 Model parameters used in an automated search for optimal model fits: initial values used and ranges allowed in minimising the sum of squared residuals between four-layer model solutions and analyser data. The last two columns of numbers are the optimal values found, without scattering and with scattering.


Figure 11 Optimal extended four-layer model solution (circles) obtained by fitting automatically to data (dots) by minimising the sum of squared residuals. The model signal strength SS is in dB. The data SS are in arbitrary units and have been linearly scaled to match model SS in dB as part of the optimisation process. Fitted parameter values are listed in Table 2. Scattering in Region 3 is also searched upon by adjusting the parameter
![]() $k_s$
.
$k_s$
.

Figure 12 Optimal previous four-layer model solution (circles) obtained by setting scattering to zero, fitted automatically to data (dots) by minimising the sum of squared residuals. Details are otherwise as in the caption to Figure 11.
5.2 Invertibility for moisture content
An important question that will be addressed in this subsection is whether signal strength and phase shifts are invertible with respect to moisture content, when using the extended four-layer model. The forward problem is solved by our received signal solution (4.1), which provides signal strength and phase shift values, given a variable moisture content and calibrated for the other parameter values affecting the signal. The inverse problem is what needs to be solved when using the microwave analyser to infer moisture content from signal strength and phase shift.

Figure 13 Extended four-layer model solutions (lines) compared with data (dot symbols). This model has scattering and sag included. The data are signal strength SS (dB) and phase shift
![]() $\Delta \phi $
(radians) at the receiving antenna. The moisture contents M used in the model are listed in the legend. Other parameter values are listed in Table 1. (Colour available online.)
$\Delta \phi $
(radians) at the receiving antenna. The moisture contents M used in the model are listed in the legend. Other parameter values are listed in Table 1. (Colour available online.)
In a previous paper [Reference Paea, Paea and McGuinness25], examples were shown where permittivity often could not be inferred solely from signal strength data. This was because there is often no unique solution for permittivity, given signal strength. Another result [Reference Paea, Paea and McGuinness25] was that phase shift had very small sensitivity to mixture conductivity. Our Figure 10 indicates that for the un-modified four-layer model, signal strength cannot, in general, be used to uniquely infer moisture content, due to the crossing of lines of constant moisture.
Now that both permittivity and conductivity are given by moisture content through our mixture models, we investigate the extended four-layer model dependence on the single variable M that is moisture content. Also important in the mixture models are the values of
![]() $D_0$
, sag, porosity, pure solid bauxite permittivity and pore water conductivity. We fit these values using Maia ship data and acknowledging that different bauxites will likely have different permittivities. Water conductivity depends strongly on dissolved salts and is also expected to vary from shipment to shipment. Zero conductivity is a good assumption for pure bauxite, and water permittivity is well known and does not vary much if dissolved salts are present. Parameter values used for model simulations are listed in Table 1.
$D_0$
, sag, porosity, pure solid bauxite permittivity and pore water conductivity. We fit these values using Maia ship data and acknowledging that different bauxites will likely have different permittivities. Water conductivity depends strongly on dissolved salts and is also expected to vary from shipment to shipment. Zero conductivity is a good assumption for pure bauxite, and water permittivity is well known and does not vary much if dissolved salts are present. Parameter values used for model simulations are listed in Table 1.
Plots equivalent to those in Figure 10, of the extended four-layer model for various moisture contents, are given in Figure 13. Including scattering has largely improved the invertibility of the signal strength data. There remain issues with noninvertibility in some smaller h ranges, especially near
![]() $h=50$
mm and 100 mm. However, at the usual load values with h values above 200 mm, signal strength data are now invertible, potentially providing unique moisture values. Phase data remain invertible – unique moisture values are, in principle, determined by data points.
$h=50$
mm and 100 mm. However, at the usual load values with h values above 200 mm, signal strength data are now invertible, potentially providing unique moisture values. Phase data remain invertible – unique moisture values are, in principle, determined by data points.
Independent laboratory measurements, taken on the day the data in Figure 13 were recorded, indicate that moisture content was typically approximately 10% (wet basis) and varied by approximately
![]() $\pm 1$
%. This guided the hand-fitting process that we used to obtain the parameter values listed in Table 1 and used to obtain the model solutions in Figure 13.
$\pm 1$
%. This guided the hand-fitting process that we used to obtain the parameter values listed in Table 1 and used to obtain the model solutions in Figure 13.
The model solutions give signal strengths in Figure 13 that are highly sensitive to moisture content. The match to signal strength data in that figure suggests that during the day that the microwave and laboratory data were gathered, moisture content varied in the range of 10–11%, assuming that other mixture properties like porosity, solid material permittivity and water purity do not change during the day. The match is not perfect and the phase shift data match indicates a slightly different moisture range of 8–10%.
5.3 Sensitivity to parameters
We investigate the sensitivity of our extended four-layer model solution (4.1) to values of the distance
![]() $D_0$
, sag, scattering, solid bauxite relative permittivity
$D_0$
, sag, scattering, solid bauxite relative permittivity
![]() $\epsilon _{rb}$
, pore water conductivity
$\epsilon _{rb}$
, pore water conductivity
![]() $\sigma _w$
and porosity n. Note that signal strength data are output in arbitrary units by the microwave analyser. In the following plots, these data have been rescaled for a visual match to solutions to our extended four-layer model, which are in dB.
$\sigma _w$
and porosity n. Note that signal strength data are output in arbitrary units by the microwave analyser. In the following plots, these data have been rescaled for a visual match to solutions to our extended four-layer model, which are in dB.
5.3.1 Spacing
 $D_0$
$D_0$
It is clear from Figure 14 that signal strength data are very sensitive to changes in the distance
![]() $D_0$
from the empty conveyor belt to the receiving antenna. Phase shift data are barely affected at the resolutions plotted. If signal strength data are to be used, accurate field measurement of
$D_0$
from the empty conveyor belt to the receiving antenna. Phase shift data are barely affected at the resolutions plotted. If signal strength data are to be used, accurate field measurement of
![]() $D_0$
is essential.
$D_0$
is essential.

Figure 14 Extended four-layer model solutions (lines) compared with data (dot symbols) for various
![]() $D_0$
values. The data are signal strength SS (dB) and phase shift
$D_0$
values. The data are signal strength SS (dB) and phase shift
![]() $\Delta \phi $
(radians) at the receiving antenna. The values of
$\Delta \phi $
(radians) at the receiving antenna. The values of
![]() $D_0$
used for each line are given in the legend in mm. Other parameter values are listed in Table 1.
$D_0$
used for each line are given in the legend in mm. Other parameter values are listed in Table 1.
5.3.2 Sag
The effects on model solutions of changing the belt sag amplitude term
![]() $S_m$
may be seen in Figure 15. Both phase shift and signal strength have visible and significant changes at ore heights above 150 mm, for a sag difference of just 20 mm. Field measurements of belt sag would help eliminate this source of uncertainty in the model.
$S_m$
may be seen in Figure 15. Both phase shift and signal strength have visible and significant changes at ore heights above 150 mm, for a sag difference of just 20 mm. Field measurements of belt sag would help eliminate this source of uncertainty in the model.

Figure 15 Extended four-layer model solutions (lines) compared with data (dot symbols) for various sag
![]() $S_m$
values. The data are signal strength SS (dB) and phase shift
$S_m$
values. The data are signal strength SS (dB) and phase shift
![]() $\Delta \phi $
(radians) at the receiving antenna. The values of
$\Delta \phi $
(radians) at the receiving antenna. The values of
![]() $S_m$
used to compute the sag for each line are given in the legend in mm. Other parameter values are listed in Table 1.
$S_m$
used to compute the sag for each line are given in the legend in mm. Other parameter values are listed in Table 1.

Figure 16 Extended four-layer model solutions for various scattering values. Signal strength SS (dB) and phase shift
![]() $\Delta \phi $
(radians) are plotted against apparent bauxite height. Data are represented by dot symbols. The values of
$\Delta \phi $
(radians) are plotted against apparent bauxite height. Data are represented by dot symbols. The values of
![]() $k_s$
used for each line for model solutions are given in the legend with units m
$k_s$
used for each line for model solutions are given in the legend with units m
![]() $^{-1}$
. Other parameter values are listed in Table 1. (Colour available online.)
$^{-1}$
. Other parameter values are listed in Table 1. (Colour available online.)
5.3.3 Scattering
Plots showing the effects of scattering on the extended four-layer model solutions can be found in Figure 16. Data have been included, although the scattering data rescaling is arbitrarily chosen to plot near the middle of the model results. There are large amplitude oscillations in signal strength visible when the damping effect
![]() $k_s$
from scattering in Region 3 is set to zero. These damp out as
$k_s$
from scattering in Region 3 is set to zero. These damp out as
![]() $k_s$
increases towards 3 m
$k_s$
increases towards 3 m
![]() $^{-1}$
, leaving behind just the oscillations that are due to reflections inside the bauxite ore layer in Region 2. These oscillations are smaller in amplitude and in wavelength than the oscillations due to reflections in Region 3. The effects of changing scattering values on phase shifts are much smaller. This set of plots is useful for understanding the effects of the two sources of oscillations in the solution, the bigger effect from reflections and (constructive and destructive) interference within Region 3, and the smaller effect from reflections and interference within Region 2. Region 3 variations in extent have a bigger effect on signal strength because there is less damping effect in air (due to scattering) in Region 3 than within the bauxite in Region 2.
$^{-1}$
, leaving behind just the oscillations that are due to reflections inside the bauxite ore layer in Region 2. These oscillations are smaller in amplitude and in wavelength than the oscillations due to reflections in Region 3. The effects of changing scattering values on phase shifts are much smaller. This set of plots is useful for understanding the effects of the two sources of oscillations in the solution, the bigger effect from reflections and (constructive and destructive) interference within Region 3, and the smaller effect from reflections and interference within Region 2. Region 3 variations in extent have a bigger effect on signal strength because there is less damping effect in air (due to scattering) in Region 3 than within the bauxite in Region 2.

Figure 17 Extended four-layer model solutions (lines) compared with data (dot symbols) for various values of solid bauxite relative permittivity
![]() $\epsilon _{rb}$
. The data are signal strength SS (dB) and phase shift
$\epsilon _{rb}$
. The data are signal strength SS (dB) and phase shift
![]() $\Delta \phi $
(radians) at the receiving antenna. The values of
$\Delta \phi $
(radians) at the receiving antenna. The values of
![]() $\epsilon _{rb}$
used for each line are given in the legend. Other parameter values are listed in Table 1.
$\epsilon _{rb}$
used for each line are given in the legend. Other parameter values are listed in Table 1.
5.3.4 Bauxite permittivity
The calibration of values of solid bauxite permittivity
![]() $\epsilon _{rb}$
is informed by the plots in Figure 17, where signal strength and phase shifts for the extended four-layer model are plotted against the apparent height h, and compared with data. The phase shift data provide good calibration information, in part because it is in radians and there is no rescaling required. However, the signal strength gives multiple values of solid permittivity for each single data point for most of the data range and is not invertible – in general, it is difficult to infer permittivity from a single signal strength data point. However, the entire graph of signal strength data against bauxite height does provide some guidance for choosing
$\epsilon _{rb}$
is informed by the plots in Figure 17, where signal strength and phase shifts for the extended four-layer model are plotted against the apparent height h, and compared with data. The phase shift data provide good calibration information, in part because it is in radians and there is no rescaling required. However, the signal strength gives multiple values of solid permittivity for each single data point for most of the data range and is not invertible – in general, it is difficult to infer permittivity from a single signal strength data point. However, the entire graph of signal strength data against bauxite height does provide some guidance for choosing
![]() $\epsilon _{rb}$
.
$\epsilon _{rb}$
.
5.3.5 Water conductivity
The electrical conductivity
![]() $\sigma _w$
is varied in the plots shown in Figure 18 and model results are compared to data. The effect on phase shifts is negligible, while the effect on signal strength is significant. When
$\sigma _w$
is varied in the plots shown in Figure 18 and model results are compared to data. The effect on phase shifts is negligible, while the effect on signal strength is significant. When
![]() $\sigma _w=0$
, there is no attenuation in the bauxite and signal strength oscillates about a mean value that increases slightly with ore height. This possibly surprising increase is due to the net effect of the ore providing a better impedance match to the transmitted wave at the receiving antenna.
$\sigma _w=0$
, there is no attenuation in the bauxite and signal strength oscillates about a mean value that increases slightly with ore height. This possibly surprising increase is due to the net effect of the ore providing a better impedance match to the transmitted wave at the receiving antenna.
5.3.6 Ore porosity
The extended four-layer model is seen to be very sensitive to the value of porosity n used for fixed moisture content
![]() $M=0.1$
in Figure 19, in both signal strength and phase shift. Since moisture content is fixed, the sensitivity is due to the diluting effect of having more air inside the ore as porosity increases, giving smaller phase shifts and smaller reductions in signal strength.
$M=0.1$
in Figure 19, in both signal strength and phase shift. Since moisture content is fixed, the sensitivity is due to the diluting effect of having more air inside the ore as porosity increases, giving smaller phase shifts and smaller reductions in signal strength.

Figure 18 Extended four-layer model solutions (lines) compared with data (dot symbols) for various values of water conductivity. The values of water conductivity
![]() $\sigma _w$
used for each line are given in the legend in S.m
$\sigma _w$
used for each line are given in the legend in S.m
![]() $^{-1}$
. Other parameter values are listed in Table 1.
$^{-1}$
. Other parameter values are listed in Table 1.

Figure 19 Extended four-layer model solutions (lines) compared with data (dot symbols) for various values of ore porosity n. The values of ore porosity n used for each line are given in the legend as volume fractions. Other parameter values are listed in Table 1.
5.3.7 Discussion of sensitivity and fit
The model is still challenged to accurately fit the signal strength behaviour versus ore height. Fits that match well for smaller heights require different parameter values to fits that match at larger heights. The four-layer model with scattering provides fits that appear better than without scattering.
The data with which we are comparing has been collected during one day of loading, and is subject to natural variations in moisture content as well as possibly random instrumental errors and variability in physical parameters like porosity and solid permittivity with time. The sensitivity of our model to moisture content exhibited in Figure 13 suggests that moisture content only varies by up to
![]() $\pm 1$
% during one day, which is consistent with laboratory measurements taken during that day that gave actual moisture values in the range
$\pm 1$
% during one day, which is consistent with laboratory measurements taken during that day that gave actual moisture values in the range
![]() $[9,11]$
%. The high sensitivity seen in Figures 14 and 15 to the distance between the bauxite and the upper antenna, as seen in
$[9,11]$
%. The high sensitivity seen in Figures 14 and 15 to the distance between the bauxite and the upper antenna, as seen in
![]() $D_0$
and sag values, means it is important to accurately measure this distance and its variability to an accuracy of millimetres rather than centimetres.
$D_0$
and sag values, means it is important to accurately measure this distance and its variability to an accuracy of millimetres rather than centimetres.
Changes in solid ore relative permittivity have significant effects on both signal strength and phase shift, with changes of order one corresponding to the scatter seen at typical operating ore heights in Figure 17. This sensitivity to the permittivity of the parent ore indicates the importance of regular re-calibration, with significant changes to the data expected if the source of the ore changes, for example, from shipload to shipload. Another option is to investigate how this parameter (solid ore permittivity) varies with source, perhaps in a study conducted alongside of the factory operations over a period of time. The salinity of the water in the ore is also poorly known and can be seen in Figure 18 to have a strong effect on signal strength but negligible effect on phase shift. In the absence of a good prior knowledge of the conductivity of pore water, regular re-calibration will be important if signal strengths are to be included in the microwave analyser’s operational inference of moisture content. An accuracy of
![]() $\pm 10$
mS.m
$\pm 10$
mS.m
![]() $^{-1}$
in values of pore water electrical conductivity is needed to get correct signal strength values in the model. Ore porosity values are closely related to conductivity, since salty pore water is the most important contributor to mixture conductivity. Figure 19 indicates that accurate values for porosity with an accuracy of
$^{-1}$
in values of pore water electrical conductivity is needed to get correct signal strength values in the model. Ore porosity values are closely related to conductivity, since salty pore water is the most important contributor to mixture conductivity. Figure 19 indicates that accurate values for porosity with an accuracy of
![]() $\pm 0.01$
are required, either by calibration or by direct measurements on offloaded ore.
$\pm 0.01$
are required, either by calibration or by direct measurements on offloaded ore.
Overall, the nonlinear and strong dependence on ore height seen in data and in model results means that it is important to accurately measure ore height, and to compensate accurately for the offset inherent in the location and timing of the ultrasound height instrument compared with the microwave receiving antenna.
5.4 Microwave frequency
The extended four-layer model provides an explanation for the nonlinear behaviour observed in data obtained when detecting microwaves that have passed through a layer of ore of thickness h. Signal strength is particularly strongly affected by reflections within the bauxite ore and in the air region between ore and receiving antenna. These reflections lead to augmentation and cancellation effects in the received signal.
One possibly helpful adjustment to improve the operations of the microwave analyser is to try changing the wavelength of the microwaves, which directly impacts these interference effects by changing the wavelengths. A lower frequency increases the wavelengths of microwaves in both air and ore, and might be hoped to reduce the amount of change of interference over the height ranges of ore typically encountered (0–300 mm). We show a series of plots in Figure 20 of strength and phase shifts for model solutions with varying moisture content for various choices of microwave operating frequencies that are smaller than used for our data.

Figure 20 Extended four-layer model solutions (lines) for various values of moisture content M. Signal frequency has been reduced to 50 MHz, 100 MHz and 200 MHz in the model. Model signal strength SS (dB) and phase shift
![]() $\Delta \phi $
(radians) at the receiving antenna are plotted against ore height h. The values of moisture content M used for each line are given in the legend as %. Other parameter values are listed in Table 1. (Colour available online.)
$\Delta \phi $
(radians) at the receiving antenna are plotted against ore height h. The values of moisture content M used for each line are given in the legend as %. Other parameter values are listed in Table 1. (Colour available online.)
An operating frequency of 50 MHz (which is getting low enough to be radio frequency) has a wavelength in air of approximately 6 m. Our model results in Figure 20 suggest that near this frequency, the assumptions of linear dependence on
![]() $SS/h$
and
$SS/h$
and
![]() $\Delta \phi / h$
will be much better approximations to actual data behaviour. Higher frequencies lead to more nonlinear behaviour in the signal strength and to less resolution in phase shift data at ore heights below 200 mm.
$\Delta \phi / h$
will be much better approximations to actual data behaviour. Higher frequencies lead to more nonlinear behaviour in the signal strength and to less resolution in phase shift data at ore heights below 200 mm.
Using much higher frequencies, in the range of 1–30 GHz, leads to more rapid oscillations in signal strength data that render it unusable for inferring moisture content. It also leads to large phase shifts that might be more difficult to accurately track electronically.
6 Conclusions
An extended four-layer model for microwave propagation through a slab region of bauxite ore has been proposed and solved exactly. The solution successfully matches the main overall characteristics of signal strength and phase shift data obtained from a microwave analyser. Accurate detection of ore moisture content using a standard setup of the analyser has been modelled here and compared with data. The use of signal strength data is not recommended for a linear regression estimate of moisture content at the data operating frequency of 900 MHz, but looks very promising at relatively low frequencies near 50 MHz.
We have sought to improve upon previous modelling work [Reference Paea, Paea and McGuinness25] by explicitly linking model results to ore moisture content and by allowing for scattering effects at the top of the ore. Automated fits for both the original and the extended models, as illustrated in Figures 11 and 12, give similar results for moisture content, 9.6% for the extended model and 10.8% for the original model. Both match laboratory results taken during the same time period, where moisture content was measured at various values lying in the range of 9–11%. Automated fitting fails to reproduce the finer details of signal strength behaviour, which are evident however (if not accurately matched) in hand-fitted parameter value sensitivity plots of model solutions.
The modelling we have undertaken, in this paper and in the previous work by Paea et al. [Reference Paea, Paea and McGuinness25], is clearly an improvement on the simple linear model that underlies the operation of a microwave analyser. Our results indicate that reflections and the consequent effects of signal augmentation and cancellation largely explain the highly oscillatory behaviour of data. However, it remains true that our extended four-layer model could be further improved to better explain the finer details of signal oscillations seen in the data.
We are focussed here on the forward problem, producing the signal given the moisture content of bauxite ore. The inverse problem remains of interest, the inference of moisture content given a measured signal. The forward modelling reveals and solves for the important role played by multiple reflections within a bauxite ore layer, as well as within the air layer between ore and receiving antenna. These reflections challenge the inverse problem, the interpretation of data to infer moisture content, especially signal strength data. Further work on the practical implications of the four-layer solution for calibrating the microwave analyser, and for using the analyser to infer moisture content in real time while loading ore, is needed. It would be useful to improve upon the current practice when using the analyses of regressing against
![]() $SS/h$
and
$SS/h$
and
![]() $\Delta \phi /h$
, the linear responses consistent with a semi-infinite model.
$\Delta \phi /h$
, the linear responses consistent with a semi-infinite model.
The model is validated by comparing it to over 20,000 data points collected during one day of operation of a microwave analyser. The model has just six adjustable parameters, so is in no danger of being over-parametrised. Furthermore, the fitting that has been done is simply to narrow down values for these parameters. The physics the modelling is based on, Maxwell’s equations and the mixture theory used to relate moisture content to electromagnetic properties, is firmly founded on experimental data and on tested knowledge about electromagnetic wave propagation.
The addition of scattering to our four-layer model was prompted by a desire to improve model fits, and it has improved them even if only slightly. The question of noninvertible signal strength results has also been allayed by adding scattering, as illustrated in Figure 13, where it is clear that a unique moisture content is associated with a given signal strength, provided ore heights are above 100 mm. In any case, any attempt to infer moisture content that uses both signal strength and phase shifts from our model should not suffer from noninvertibility, as the phase shifts resolve any questions about which of several moisture contents to use.
The four-layer model with scattering provides the best fits we have obtained, but the model has taken serious liberties with how it deals with scattering effects. This may be why our model still fails to provide a very accurate match in fine detail to data over the full range of ore heights. A major simplification that remains in our model is that it is one-dimensional in space and that interfaces are normal to the direction of wave propagation. Improvements might include a higher-dimensional treatment of the effects of scattering and curvature at the bauxite ore surface, and allow for the geometry of the conveyor belt and bauxite ore load.
The modelling we have conducted does not consider the possibly important role played by noise in obtaining analyser data. Future modelling with a focus on the inverse problem might profitably investigate the importance of signal-to-noise ratios, especially for very wet ores, as well as the effects of scattering on noise. It would also be useful to investigate the implications of our four-layer model for using data obtained using two different operating frequencies to improve estimates of moisture content.
Appendix A. Four-layer model and solutions
In this Appendix, we summarise the method for solving our four-layer model, for completeness. The description here follows that of Paea et al. [Reference Paea, Paea and McGuinness25].
We choose Cartesian axes so that, in Region 1 of Figure 2,
![]() $x \leqslant 0 $
and the upwards-travelling incident radiation is
$x \leqslant 0 $
and the upwards-travelling incident radiation is
 $$ \begin{align*} \mathbf{H}_i &= ( 0, e^{ikx}, 0)e^{-i\omega t} , \\ \mathbf{E}_i &= ( 0, 0, E_{1+} e^{ikx})e^{-i\omega t} , \end{align*} $$
$$ \begin{align*} \mathbf{H}_i &= ( 0, e^{ikx}, 0)e^{-i\omega t} , \\ \mathbf{E}_i &= ( 0, 0, E_{1+} e^{ikx})e^{-i\omega t} , \end{align*} $$
with magnetic field amplitude set to one. Note that the linearity of the equations being solved, and our later normalisation with respect to the solution when
![]() $h=0$
, make this amplitude irrelevant. The downwards-travelling reflected wave of unknown amplitude R is
$h=0$
, make this amplitude irrelevant. The downwards-travelling reflected wave of unknown amplitude R is
 $$ \begin{align*} \mathbf{H}_r &= ( 0, Re^{-ikx}, 0 )e^{-i\omega t} , \\ \mathbf{E}_r &= ( 0, 0, E_{1-} e^{-ikx} )e^{-i\omega t} , \end{align*} $$
$$ \begin{align*} \mathbf{H}_r &= ( 0, Re^{-ikx}, 0 )e^{-i\omega t} , \\ \mathbf{E}_r &= ( 0, 0, E_{1-} e^{-ikx} )e^{-i\omega t} , \end{align*} $$
with
and
The value of
![]() $E_{1+} $
follows from setting the upwards-travelling magnetic field amplitude to one, together with Maxwell’s equation
$E_{1+} $
follows from setting the upwards-travelling magnetic field amplitude to one, together with Maxwell’s equation
![]() $\nabla \times \mathbf {E} = - \mu \partial \mathbf {H}/ \partial t $
relating electric and magnetic fields. Equation (2.2) becomes
$\nabla \times \mathbf {E} = - \mu \partial \mathbf {H}/ \partial t $
relating electric and magnetic fields. Equation (2.2) becomes
 $$\begin{align*}k^2 = \omega^2 \epsilon_0 \mu_0 = \frac{\omega^2}{c^2} , \end{align*}$$
$$\begin{align*}k^2 = \omega^2 \epsilon_0 \mu_0 = \frac{\omega^2}{c^2} , \end{align*}$$
where
![]() $k=2\pi /\lambda $
is the wavenumber in free space or air and
$k=2\pi /\lambda $
is the wavenumber in free space or air and
![]() $\lambda $
is the wavelength in free space. Furthermore,
$\lambda $
is the wavelength in free space. Furthermore,
![]() $k=\omega /c = \omega \sqrt {\epsilon _0 \mu _0 }$
, where c is the speed of light. The impedance
$k=\omega /c = \omega \sqrt {\epsilon _0 \mu _0 }$
, where c is the speed of light. The impedance
is a useful combination of parameter values since it appears a number of times.
In Region 2 of Figure 2, where
![]() $0 \leqslant x \leqslant h$
, the waves are travelling through the bauxite mixture, with fields
$0 \leqslant x \leqslant h$
, the waves are travelling through the bauxite mixture, with fields
where
![]() $E(x)$
in the bauxite can be written in the form
$E(x)$
in the bauxite can be written in the form
Equation (2.2) gives
where the dissipation is
![]() ${\cal D}_b = \sigma _b/(\omega \epsilon _b)$
in the bauxite ore mixture. The real part of
${\cal D}_b = \sigma _b/(\omega \epsilon _b)$
in the bauxite ore mixture. The real part of
![]() $k_b$
can be written
$k_b$
can be written
 $$\begin{align*}\operatorname{Re} (k_b) = \omega \sqrt{ \frac{\epsilon_b \mu_b }{2}} ( \sqrt{1 + {\cal D}_b^2 } + 1 )^{1/2} ,\end{align*}$$
$$\begin{align*}\operatorname{Re} (k_b) = \omega \sqrt{ \frac{\epsilon_b \mu_b }{2}} ( \sqrt{1 + {\cal D}_b^2 } + 1 )^{1/2} ,\end{align*}$$
while the imaginary part is
 $$\begin{align*}\operatorname{Im} (k_b) = \omega \sqrt{ \frac{\epsilon_b \mu_b }{2}} ( \sqrt{1 + {\cal D}_b^2} - 1 )^{1/2} .\end{align*}$$
$$\begin{align*}\operatorname{Im} (k_b) = \omega \sqrt{ \frac{\epsilon_b \mu_b }{2}} ( \sqrt{1 + {\cal D}_b^2} - 1 )^{1/2} .\end{align*}$$
In Region 3 of Figure 2 where
![]() $h \leqslant x \leqslant D $
, the radiation travelling upwards from the bauxite is
$h \leqslant x \leqslant D $
, the radiation travelling upwards from the bauxite is
 $$ \begin{align*} \mathbf{H}_t &= ( 0, T_3 e^{ikx}, 0)e^{-i\omega t} \\ \mathbf{E}_t &= ( 0, 0, E_{3+} e^{ikx})e^{-i\omega t} , \end{align*} $$
$$ \begin{align*} \mathbf{H}_t &= ( 0, T_3 e^{ikx}, 0)e^{-i\omega t} \\ \mathbf{E}_t &= ( 0, 0, E_{3+} e^{ikx})e^{-i\omega t} , \end{align*} $$
and the travelling wave reflected downwards from the receiving antenna is
 $$ \begin{align*} \mathbf{H}_{r3} &= ( 0, R_3 e^{-ikx}, 0 )e^{-i\omega t} ,\\ \mathbf{E}_{r3} &= ( 0, 0, E_{3-} e^{-ikx})e^{-i\omega t} \end{align*} $$
$$ \begin{align*} \mathbf{H}_{r3} &= ( 0, R_3 e^{-ikx}, 0 )e^{-i\omega t} ,\\ \mathbf{E}_{r3} &= ( 0, 0, E_{3-} e^{-ikx})e^{-i\omega t} \end{align*} $$
with
![]() $ E_{3+} = -T_3 Z_0 $
and
$ E_{3+} = -T_3 Z_0 $
and
![]() $ E_{3-} = R_3 Z_0 $
.
$ E_{3-} = R_3 Z_0 $
.
In Region 4 of Figure 2 where
![]() $x \geqslant D$
, the receiving antenna is modelled as a semi-infinite material with relatively high electrical conductivity, so that
$x \geqslant D$
, the receiving antenna is modelled as a semi-infinite material with relatively high electrical conductivity, so that
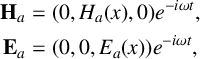 $$ \begin{align*} \mathbf{H}_a & = (0,H_a(x) , 0) e^{-i \omega t} , \\ \mathbf{E}_a & =(0,0, E_a(x) ) e^{-i \omega t}, \end{align*} $$
$$ \begin{align*} \mathbf{H}_a & = (0,H_a(x) , 0) e^{-i \omega t} , \\ \mathbf{E}_a & =(0,0, E_a(x) ) e^{-i \omega t}, \end{align*} $$
and we write the upwards-travelling electric field in the antenna in the form
Equation (2.2) gives
The electromagnetic properties of the receiving antenna are not known to us. The model results are not very sensitive to these parameter values, which are listed in Table 1. Since the root
![]() $k_a$
has a positive imaginary part,
$k_a$
has a positive imaginary part,
![]() $E_a$
vanishes as
$E_a$
vanishes as
![]() $x \to \infty $
.
$x \to \infty $
.
There are six unknown constants R,
![]() $E_{2+}$
,
$E_{2+}$
,
![]() $E_{2-}$
,
$E_{2-}$
,
![]() $T_3 $
,
$T_3 $
,
![]() $R_3$
and
$R_3$
and
![]() $E_{4+}$
. Their values are provided by the boundary conditions which give six linear equations that are to be solved simultaneously. The solution we are interested in here is the field amplitude
$E_{4+}$
. Their values are provided by the boundary conditions which give six linear equations that are to be solved simultaneously. The solution we are interested in here is the field amplitude
![]() $E_{4+}$
detected at the receiving antenna.
$E_{4+}$
detected at the receiving antenna.
Continuity of E and H at
![]() $x=0$
, together with the use of Maxwell’s equation
$x=0$
, together with the use of Maxwell’s equation
gives the boundary conditions
Continuity of E and H at
![]() $x=h$
gives the boundary conditions
$x=h$
gives the boundary conditions
Continuity of electric and magnetic tangential fields at
![]() $x=D$
gives the boundary conditions
$x=D$
gives the boundary conditions
Here,
![]() $Z_b = \mu _b \omega / k_b $
is the impedance of the bauxite mixture and
$Z_b = \mu _b \omega / k_b $
is the impedance of the bauxite mixture and
![]() $Z_a = \mu _a \omega / k_a $
is the impedance of the receiving antenna.
$Z_a = \mu _a \omega / k_a $
is the impedance of the receiving antenna.
Then (A.2)–(A.7) can be written in matrix form:
 $$ \begin{align*} \left(\begin{array}{cccccc} 1, & 1, & -Z_0, & 0, & 0, & 0 \\ 1, & -1, & Z_b, & 0, & 0, & 0 \\ e^{i k_b h} , & -e^{-i k_b h} , & 0,& Z_b e^{i k h} , & Z_b e^{-i k h} , & 0\\ e^{i k_b h} , & e^{-i k_b h} , & 0,& Z_0 e^{i k h} , & -Z_0 e^{-i k h} , & 0\\ 0,&0,&0,&Z_a e^{i k D} , & Z_a e^{-i k D}, & 1 \\ 0,&0,&0,&Z_0 e^{i k D} , & -Z_0 e^{-i k D}, & 1 \\ \end{array} \right ) \left ( \begin{array}{c} E_{2+}\\ E_{2-} \\ R \\ T_3 \\ R_3 \\ E_{4+} \end{array} \right ) = \left ( \begin{array}{c } -Z_0\\ -Z_b \\ 0 \\ 0 \\ 0 \\ 0 \end{array} \right), \end{align*} $$
$$ \begin{align*} \left(\begin{array}{cccccc} 1, & 1, & -Z_0, & 0, & 0, & 0 \\ 1, & -1, & Z_b, & 0, & 0, & 0 \\ e^{i k_b h} , & -e^{-i k_b h} , & 0,& Z_b e^{i k h} , & Z_b e^{-i k h} , & 0\\ e^{i k_b h} , & e^{-i k_b h} , & 0,& Z_0 e^{i k h} , & -Z_0 e^{-i k h} , & 0\\ 0,&0,&0,&Z_a e^{i k D} , & Z_a e^{-i k D}, & 1 \\ 0,&0,&0,&Z_0 e^{i k D} , & -Z_0 e^{-i k D}, & 1 \\ \end{array} \right ) \left ( \begin{array}{c} E_{2+}\\ E_{2-} \\ R \\ T_3 \\ R_3 \\ E_{4+} \end{array} \right ) = \left ( \begin{array}{c } -Z_0\\ -Z_b \\ 0 \\ 0 \\ 0 \\ 0 \end{array} \right), \end{align*} $$
and represented in augmented matrix form as
 $$ \begin{align} \left(\begin{array}{cccccc|c} 1, & 1, & -Z_0, & 0, & 0, & 0 & -Z_0\\ 1, & -1, & Z_b, & 0, & 0, & 0 & -Z_b\\ e^{i k_b h} , & -e^{-i k_b h} , & 0,& Z_b e^{i k h} , & Z_b e^{-i k h} , & 0& 0\\ e^{i k_b h} , & e^{-i k_b h} , & 0,& Z_0 e^{i k h} , & -Z_0 e^{-i k h} , & 0& 0\\ 0,&0,&0,&Z_a e^{i k D} , & Z_a e^{-i k D}, & 1 & 0\\ 0,&0,&0,&Z_0 e^{i k D} , & -Z_0 e^{-i k D}, & 1 & 0 \end{array} \right ). \end{align} $$
$$ \begin{align} \left(\begin{array}{cccccc|c} 1, & 1, & -Z_0, & 0, & 0, & 0 & -Z_0\\ 1, & -1, & Z_b, & 0, & 0, & 0 & -Z_b\\ e^{i k_b h} , & -e^{-i k_b h} , & 0,& Z_b e^{i k h} , & Z_b e^{-i k h} , & 0& 0\\ e^{i k_b h} , & e^{-i k_b h} , & 0,& Z_0 e^{i k h} , & -Z_0 e^{-i k h} , & 0& 0\\ 0,&0,&0,&Z_a e^{i k D} , & Z_a e^{-i k D}, & 1 & 0\\ 0,&0,&0,&Z_0 e^{i k D} , & -Z_0 e^{-i k D}, & 1 & 0 \end{array} \right ). \end{align} $$
A.1. Four-layer model solution
Row reduction of the augmented matrix (A.8) can be used to write it in upper triangular form, allowing back-substitution to solve for all of the unknown field amplitudes. In particular, the solution for the electric field at the receiving antenna can be written in the form [Reference Paea, Paea and McGuinness25]
 $$ \begin{align*} E_a = E_{4+} = \frac{ 8 Z_0^2 Z_a Z_b \; e^{ik(D-h)} e^{ik_b h}}{F} , \end{align*} $$
$$ \begin{align*} E_a = E_{4+} = \frac{ 8 Z_0^2 Z_a Z_b \; e^{ik(D-h)} e^{ik_b h}}{F} , \end{align*} $$
where
 $$ \begin{align*} F &= (Z_b^2 - Z_0^2)(Z_0-Z_a) ( e^{2ik_b h} - 1) e^{2ik(D-h)} \nonumber \\ & \quad + [ (Z_0-Z_b)^2 e^{2i k_b h} - (Z_0+Z_b)^2](Z_0 + Z_a). \end{align*} $$
$$ \begin{align*} F &= (Z_b^2 - Z_0^2)(Z_0-Z_a) ( e^{2ik_b h} - 1) e^{2ik(D-h)} \nonumber \\ & \quad + [ (Z_0-Z_b)^2 e^{2i k_b h} - (Z_0+Z_b)^2](Z_0 + Z_a). \end{align*} $$
A.2. Belt sag
We here consider the possibility that as the amount of ore on the conveyor belt increases, the ore weight causes the belt to sag between the rollers that drive it. This is a summary of the approach described by Paea et al. [Reference Paea, Paea and McGuinness25]. The microwave analyser is mounted between rollers. Adding belt sag to our model gives a small improvement to fits to signal strength data, by allowing a difference between heavily loaded and lightly loaded conveyor belts. We compute the sag using the formula
so that sag depends on the true height h of bauxite ore present on the belt. Model matches to data were improved with the choices
![]() $S_m = 40$
mm for maximum sag amplitude,
$S_m = 40$
mm for maximum sag amplitude,
![]() $h_m=200$
mm for the middle of the sag region and
$h_m=200$
mm for the middle of the sag region and
![]() $S_e=100$
mm for the extent of the region over which sagging occurs. These values will be used as default values, unless otherwise stated, in the remainder of this paper. Figure 21 illustrates the dependence of sag on h given by (A.9) and plots the true bauxite height against the height measured in the data. Conversations with an engineer from the bauxite company suggest that belt sag is unlikely to exceed 30 mm.
$S_e=100$
mm for the extent of the region over which sagging occurs. These values will be used as default values, unless otherwise stated, in the remainder of this paper. Figure 21 illustrates the dependence of sag on h given by (A.9) and plots the true bauxite height against the height measured in the data. Conversations with an engineer from the bauxite company suggest that belt sag is unlikely to exceed 30 mm.

Figure 21 Belt sag versus true bauxite height h, and the true bauxite height versus the height measured in strength and phase data. The dashed line in panel (b) shows when true height is equal to data height.
Data heights are measured using an ultrasound device attached to the upper receiving antenna, pointing downwards to the top of the bauxite layer. Hence, sag will have two effects on the four-layer model. It will increase the distance D from the bottom of the bauxite layer to the receiving antenna, as
and it will make the measured data heights
![]() $h_m$
smaller than the true thickness values h, so that
$h_m$
smaller than the true thickness values h, so that
All plots that appear later in this manuscript are against data or apparent
![]() $h_m$
values, that is,
$h_m$
values, that is,
![]() $h - $
sag values are used for plotting model results, to be able to compare them with data.
$h - $
sag values are used for plotting model results, to be able to compare them with data.
Acknowledgements
We are grateful to John and Hilary Ockendon (Mathematical Institute, University of Oxford) for conversations during an online Study Group in India that led directly to our approach here. Mark McGuinness is grateful to the MACSI group in the Department of Mathematics and Statistics at the University of Limerick in Ireland for hosting the original Study Group that led to this work, and for their continued support.





















































