Introduction
The Qinghai-Tibetan Plateau (QTP) in western China, situated at 4000 m a.s.l., is the highest plateau in the world, with an area of ∽ 2.3 x 106 km2. Its high elevation plays a key role in the climate and environment of the plateau. Recent surveys show that the warming trend experienced in high-altitude regions appears to be greater than that at low altitude (Reference Beniston, Diaz and BradleyBeniston and others, 1997; Reference Diaz and BradleyDiaz and Bradley, 1997). This suggests that the QTP is one of the most sensitive areas to global climate change (Reference Liu and ZhangLiu and Zhang, 1998; Reference Liu and ChenLiu and Chen, 2000).
The vast cryosphere, including permafrost, glaciers and lake ice, is one of the main features of the QTP because of its unique geological and geographic settings. Changes in the cryospheric components have significant impacts on land surface hydrology, ecosystems, landscape and geomorphologic processes, and engineering constructions. Comparing previous work on the permafrost and glaciers of the QTP (e.g. Reference Wu, Zhang and LiuWu and others, 2010; Reference Cheng and JinCheng and Jin, 2013; Reference Wang, Siegert, Zhou and FrankeWang and others, 2013a; Reference YuYu and others, 2013), only a few studies in the literature deal with lake ice on the plateau.
Alpine lakes are widespread on the QTP and are often covered by ice for 5-7 months of the year because of the severe cold weather. The presence of ice cover on a lake can greatly reduce the amount of solar radiation passing into the lake due to the higher albedo of ice, thus impeding heat exchange, as well as hydrodynamic and transport processes between the overlying atmosphere and the underlying water (Reference Stefanovic and StefanStefanovic and Stefan, 2002). Recent studies show that change in ice cover is a good indicator of climate change, because the freeze-thaw cycles of ice cover result from local meteorological conditions, in particular, air temperature (Reference Robertson, Ragotzkie and MagnusonRobertson and others, 1992; Reference Johnson and StefanJohnson and Stefan, 2006).
Natural freshwater lake ice on the QTP is composed of pure ice and gas bubbles (Reference Huang, Han, Shi, Niu, Deng and LiHuang and others, 2013a). Studies suggest that the thermophysical properties of ice are sensitive to ice temperature (Reference YenYen, 1981; Reference FukusakoFukusako, 1990). However, these studies deal with a wide range of ice temperatures, which is not suitable for studying in detail the characteristics of natural lake ice thermal properties with a narrow range of ice temperatures. Thus, it is useful to investigate the thermal properties of QTP lake ice, in particular, at higher temperature regimes, as global warming is exposing lake ice to prolonged periods of warmth.
Thermal diffusivity, which measures the ability of a material to conduct thermal energy relative to its ability to store the energy, is a directly measurable thermal property (Reference YenYen, 1981) and a key factor in the heat transfer process. Our study of thermal diffusivity of lake ice is important, because the formation of lakes on the QTP has increased as a result of an unstable permafrost and climate warming (Reference Lin, Niu, Xu, Xu and WangLin and others, 2010). Furthermore, thermal diffusivity is useful for the development of lake-ice models to simulate ice-growth processes in high-boreal lakes (Reference Duguay, Flato, Jeffries, nard, Rouse and MorrisDuguay and others, 2003), as well as the heat budget of the air–ice–water system on the QTP. In this study, we evaluate the thermal diffusivity of lake ice using the optimal control method, to improve our understanding of the thermal processes of lake ice on the QTP, in particular, in the higher temperature regime.
We first analyze in situ measurements for a typical thermokarst lake in the Beiluhe basin of the QTP. Secondly, we apply an optimal control model and, based on the measured ice temperature data, examine the thermal diffusivity change of the lake ice with ice temperature on the plateau. We then compare our results with previous numerical and experimental findings, and evaluate the characteristics of the thermal diffusivity of thermokarst lake ice in the Beiluhe basin. We also discuss the influence of gas bubbles on the thermal diffusivity.
Study Area
The Beiluhe basin is located on the central QTP, with a mean annual air temperature of –3.8°C and a mean annual ground temperature range of -1.8 to -0.5°C (Reference Huang, Li, Han, Niu, Lin and LeppärantaHuang and others, 2012). We choose a typical thermokarst lake, BLH-A lake (34°49.5 ′N, 92°55.4 ′E), with a roughly elliptical shape as our study area in the Beiluhe basin (Fig. 1). This lake has an area of ~15 000 m2 and the lake shore is ~100 m away from the Qinghai-Tibet railway. Detailed descriptions of the lake can be found, for example, in Reference Lin, Niu, Xu, Xu and WangLin and others (2010, Reference Lin, Niu, Liu and Lu2011) and Reference Huang, Han, Shi, Niu, Deng and LiHuang and others (2012). BLH-A lake is a perennial lake with a water depth of up to 2 m. Ice on this lake is considered to be freshwater ice (Reference Huang, Han, Shi, Niu, Deng and LiHuang and others, 2013a), so the influence of the water and ice geochemistry can be ignored in this study. The average ice thickness is ~0.45-0.5 m throughout the cold season. In general, a stable ice cover forms in early November and melts in late April or early May the following year. The upper layer beneath the water in this thermokarst lake consists of 0.6 m of peaty soil underlain by a mixture of fine gravel, sand and mudstone (Reference Lin, Niu, Liu and LuLin and others, 2011). There is no snow cover on the ice surface, largely owing to little snowfall and a strong prevailing wind (Reference Huang, Li, Han, Niu, Lin and LeppärantaHuang and others, 2012).

Fig. 1. Aerial view of the study area. The locations of BLH-A lake and the Beiluhe Research Station are shown by a red star and a green circle, respectively. Image courtesy of Google Earth, 26 August 2011.
Data Collection and Analysis
Because of the distinct meteorological and stratigraphic features of the QTP, the variation of air, ice and water temperature, and the inner structure within ice (e.g. gas bubble shape and size, gas content, ice crystal type and crystal size) in BLH-A lake must possess their own characteristics (Reference Huang, Li, Han, Niu, Lin and LeppärantaHuang and others, 2012). The growth and decay of lake ice in the QTP are dominated by the thermal process, temperature in particular. We therefore focus on the temperature of lake ice on the QTP. A thermistor cable was deployed at the deepest point (~2 m) at the southeast end of BLH-A lake (Reference Huang, Li, Han, Niu, Lin and LeppärantaHuang and others, 2012). A series of air, ice and under-ice water temperatures were measured from late October 2010 to June 2011 through the thermistor cable. The ice and under-ice water temperatures were recorded automatically (with a precision of 0.1°C) every 30 min, with a vertical interval of 5 cm.
The change of temperature, and the daily temperature difference, in air, ice and in water under the ice is shown in Figure 2 for the period 20 October 2010 to 20 April 2011. We process the data using the moving average method with a window of 24 hours to remove the effect of outliers and missing measurements. The air temperature at 150 cm above the ice surface, and the surface ice temperature change substantially and at a similar rate. However, with increasing depth, the ice/water temperature becomes higher and much more stable, and the temperature change is smaller. This phenomenon may be explained by the strong solar radiation in the daytime and the insulation of the ice cover (Reference Nicolaus, Hudson, Gerland and MunderlohNicolaus and others, 2010). The variation of daily temperature difference in Figure 2 (blue line) also illustrates the same trend. The daily temperature differences decrease with increasing depth; there is almost no change in the daily water temperature difference at 70 cm below the ice surface. In general, we observe that the daily water temperature variability decreases with water depth.

Fig. 2. Variation of air and ice/water temperature (black line) and their daily temperature difference (blue line) from a thermistor cable in BLH-A lake.
Based on the analysis of the temperature of the air, ice and water under the ice, the temperature decreases from early November to late January, then remains stable until March and then begins to increase again. It is difficult to identify exactly when the ice is growing simply based on the decreasing air temperature, because air temperature alone is not sufficient to support thermodynamic ice growth (Reference WangWang and others, 2013b). However, we are still able to analyze the temperature data to identify the growth period before ice melted. Based on the above discussion, we define the ice layer used in our study as ranging from 5 cm under the ice surface to the position of the temperature sensor embedded in the bottom of the ice, measured during the night (21:00-5:00). This ensures that the ice temperature data in our calculations are less affected by the air temperature, under-ice water and solar radiation. Furthermore, 0°C is considered as the freezing point of BLH-A lake ice, which is used to distinguish the ice/water interface and the position of the temperature sensor embedded in the bottom of the ice.
In addition to ice temperature, the inner structure of the ice can also help us understand ice growth processes. As a composite material, the various thermal, physical, biological and geochemical processes of lake ice are strongly affected by its composition and structure (Reference Wang, Carson, North and ClelandWang and others, 2008). It is thought that lake ice in the QTP has high porosity and large gas pores (Reference Huang, Li, Han, Niu, Lin and LeppärantaHuang and others, 2012), which is likely to be an important influencing factor on the thermal diffusivity of BLH-A lake ice. We therefore present photographs of gas bubbles (Fig. 3) from ice samples ~3m away from the thermistor cable taken in BLH-A lake on 9 December 2010 (during the phase of rapid ice growth). The photographs illustrate the unique characteristics of gas bubbles. It is surprising that the gas bubbles from the two ice samples are completely different, although the sampling sites are only ~3m apart in the same lake. It is clear that the size and volume of the rachis-shaped bubbles (Fig. 3a) are greater than those of the dotted-line shaped bubbles (Fig. 3b). The rachis-shaped bubbles are relatively large, have a regular pattern of an oblate round cake or a quasi-sphere with an even top and a circular bottom (1-5 cm in diameter and 1-2 cm high) and are connected to each other in series. The dotted-line shaped bubbles are smaller, consist of vertical strings of tiny gas pockets with diameters of 0.3-2.5 mm and can be considered as ‘cylindrical bubbles’ (specifically, vertical spherical bubble strings) with aspect ratios (the ratio of the width of a shape to its height) of 100-200 (Reference Huang, Li, Han, Niu, Lin and LeppärantaHuang and others, 2012).

Fig. 3. Photographs of gas bubbles with (a) rachis and (b) dotted-line shapes from BLH-A lake ice taken on 9 December 2010. Gas and pure ice are shown in white and black, respectively.
Thermal Diffusivity Model
The heat transfer process within the ice in the vertical direction is governed by the classical one-dimensional heat conduction equation (Reference Reid and CroutReid and Crout, 2008):
where ρ is ice density, c is the specific heat capacity, T is ice temperature, z is the vertical coordinate, positive downward, t is the time, kis the thermal conductivity and I is the heat source term, equivalent to the fraction of the down-welling radiation flux that has penetrated to depth z. Because we consider heat transfer only in the middle ice layer (from 5 cm under the ice surface to the position of the temperature sensor embedded in the bottom of the ice) during the night, the heat source term, primarily the solar radiation, can be ignored in the heatconduction equation.
Thus, Eqn (1) can be expressed as:
In our numerical calculations we consider small time (10 s) result, ice temperature changes slightly for each spatial step, and the corresponding change of thermal conductivity of ice becomes very small and its spatial derivative can be safely ignored.
temperature. Previous studies have also applied this simplified heat conduction equation (e.g. Reference SemtnerSemtner, 1976). The heat conduction equation with initial and boundary conditions is
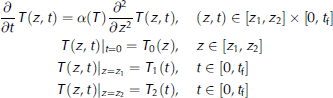
where ![]() is the thermal diffusivity of ice, z is the spatial variable with z ϵ [z
1, z2], z1 and z
2 are the upper and lower boundaries, t is the time variable with t ϵ [0, t
f], and t
f is the final time for measurement. The initial and boundary conditions are all given functions through interpolation and the fitting of the measured ice temperature. Because α{T), T
0(z), T
1
(t) and T2(t) are all continuous and differentiable within the model domain, satisfying T
0(z1) = T1(0), T
0(z
2) = T2(0), Eqn (3) has a unique solution. In this paper, we use a simple linear function to describe the relationship between the thermal diffusivity and ice temperature: α{T) = a + bT. In this case, (a, b) are the parameters to be determined.
is the thermal diffusivity of ice, z is the spatial variable with z ϵ [z
1, z2], z1 and z
2 are the upper and lower boundaries, t is the time variable with t ϵ [0, t
f], and t
f is the final time for measurement. The initial and boundary conditions are all given functions through interpolation and the fitting of the measured ice temperature. Because α{T), T
0(z), T
1
(t) and T2(t) are all continuous and differentiable within the model domain, satisfying T
0(z1) = T1(0), T
0(z
2) = T2(0), Eqn (3) has a unique solution. In this paper, we use a simple linear function to describe the relationship between the thermal diffusivity and ice temperature: α{T) = a + bT. In this case, (a, b) are the parameters to be determined.
Optimal Control Model
To examine the change of thermal diffusivity of lake ice with ice temperature in BLH-A lake, an optimal control model is applied in conjunction with measured ice temperature data, which can be expressed as
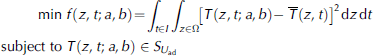
where T(z,t; a, b) is the calculated ice temperature from Eqn (3), and ![]() is a fitted function of the measured ice temperature. The purpose of the model is to minimize the difference between the calculated and measured ice temperature. The optimal control method has been used successfully to solve several problems in the numerical calculations (Reference Bai, Li, Han and LuBai and others, 2005, Reference Bai, Li, Lu, Zhang and Feng2007; Reference Shi, Li, Feng, Bai and YangShi and others, 2013) as well as in the theoretical analyses (Reference Lv, Feng and LiLv and others, 2008; Reference Fang, Wang, Feng and LiFang and others, 2011; Reference Tan, Lu, Li, Feng and WangTan and others, 2012) of ice. In the model
is a fitted function of the measured ice temperature. The purpose of the model is to minimize the difference between the calculated and measured ice temperature. The optimal control method has been used successfully to solve several problems in the numerical calculations (Reference Bai, Li, Han and LuBai and others, 2005, Reference Bai, Li, Lu, Zhang and Feng2007; Reference Shi, Li, Feng, Bai and YangShi and others, 2013) as well as in the theoretical analyses (Reference Lv, Feng and LiLv and others, 2008; Reference Fang, Wang, Feng and LiFang and others, 2011; Reference Tan, Lu, Li, Feng and WangTan and others, 2012) of ice. In the model ![]() the subscripts l "and u , denote the lower7 and upper limits respectively. The domain of parameter (a, b) is estimated from a ve of thermal diffusivities of ice from previous studies (Reference YenYen, 1981
Reference Bai, Li, Han and LuBai and others 2005
Reference Chen, Morikawa, Kishi and HashimotoChen an p others 2005) We defined S
U =
{T{ s, b)} so that S
U is a set including all the solutions of Eqn (3). When solving
Eqn (3), small time (10s) and space (0.5cm) intervals are employed in the iterative process. However, the optimal control model is applied to available in situ data that have 5 cm of spatial and 30 min of temporal resolutions.
the subscripts l "and u , denote the lower7 and upper limits respectively. The domain of parameter (a, b) is estimated from a ve of thermal diffusivities of ice from previous studies (Reference YenYen, 1981
Reference Bai, Li, Han and LuBai and others 2005
Reference Chen, Morikawa, Kishi and HashimotoChen an p others 2005) We defined S
U =
{T{ s, b)} so that S
U is a set including all the solutions of Eqn (3). When solving
Eqn (3), small time (10s) and space (0.5cm) intervals are employed in the iterative process. However, the optimal control model is applied to available in situ data that have 5 cm of spatial and 30 min of temporal resolutions.
Based on the solutions from the optimal control model, increasing ice tegime (Fig. 4). oachi p dly d value of thermal diffu ngM of f pe sh wa er ppr ng th ice tem ature regime, the th ty ermal diffusivity changes almost linea p y with ice temperature.
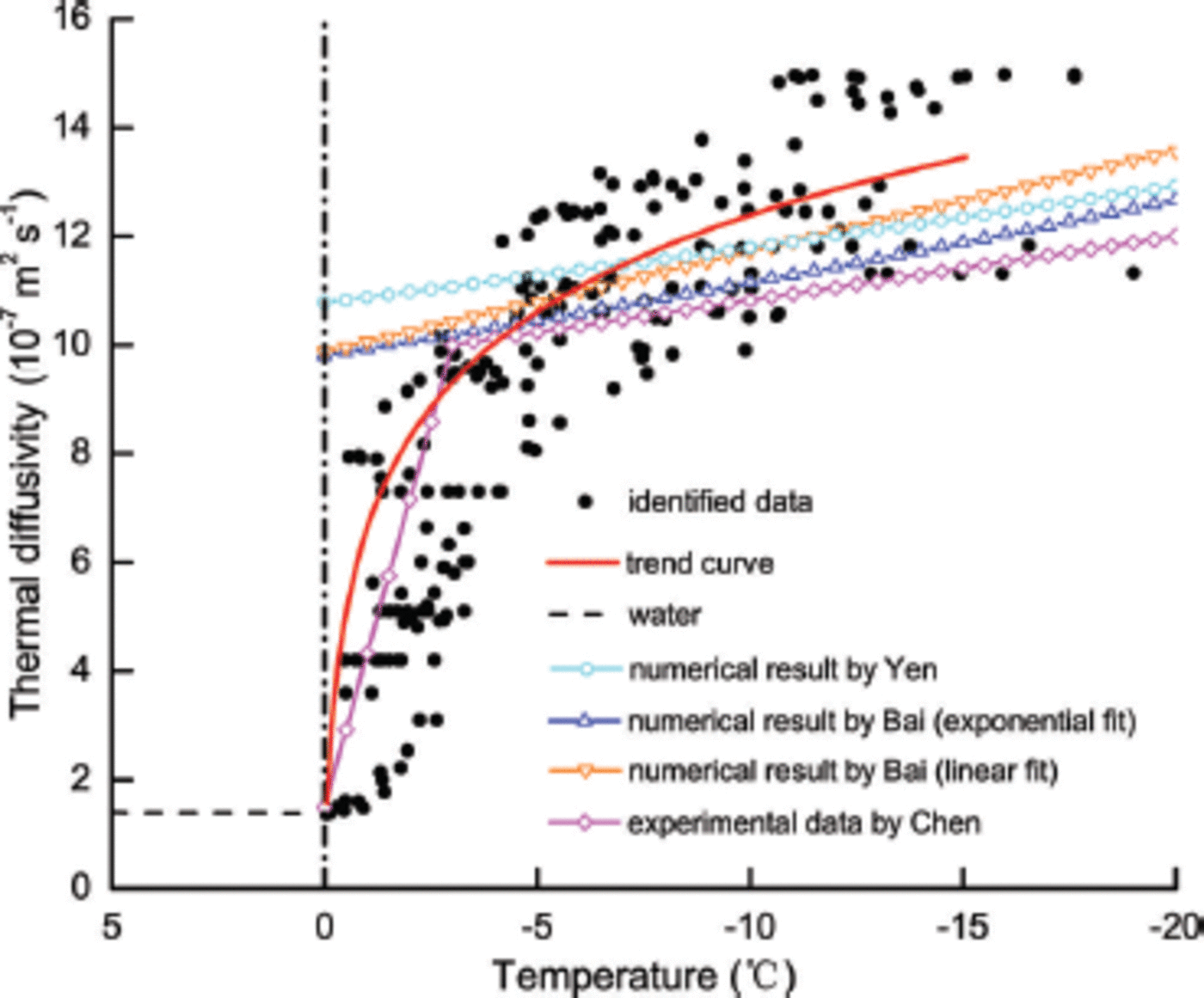
Fig. 4. The variationof thermal diffusivity with ice temperature in BLH-A lake ice.
We can express these results by fitting a trend line (red line in Fig. 4) as follows:
where α(T) is thermal diffusivity of ice (m2 s–1) and Tis ice temperature (°C).
We have presented a general description of the variability of thermal diffusivity with ice temperature in our study. Although a more accurate model with greater physical insight should be formulated to clarify the thermal diffusivity of BLH-A lake ice in the future, this simpler formula can help provide a general idea of how thermal diffusivity changes with ice temperature.
Discussion
Our thermal diffusivity results fare well compared with the numerical and experimental results reported in the literature (Fig. 4) (Reference YenYen, 1981; Reference Koubyshkin and SazonovKoubyshkin and Sazonov, 2004; Reference Bai, Li, Han and LuBai and others, 2005; Reference Chen, Morikawa, Kishi and HashimotoChen and others, 2005). The changes in the thermal diffusivity with ice temperature in the previous numerical studies (e.g. Reference YenYen 1981; Reference Koubyshkin and SazonovKoubyshkin and Sazonov, 2004; Reference Bai, Li, Han and LuBai and others, 2005) are similar. The thermal diffusivity of ice decreases with increasing ice temperature, and reaches a value close to 10.0 x 10-7m2 s–1 as ice temperature approaches the freezing point (Fig. 4). These previous studies were conducted within a wide temperature range, and therefore did not show the change of thermal diffusivity of lake ice with higher temperatures. It is therefore difficult to explain why the thermal diffusivity in these studies changed abruptly from ice (-10.0 x 10-7m2 s–1) to water (~1.35 x 10-7m2 s–1) at the freezing point, which is the limitation of the previous numerical results.
The experimental data determined by temperature wave analysis (Reference Chen, Morikawa, Kishi and HashimotoChen and others, 2005) are very different from the numerical results, especially at the higher temperature range (-3 to 0°C). The experimental results in Figure 4 show that the thermal diffusivity decreases rapidly to the value of thermal diffusivity of water when ice temperature approaches the freezing point. Nevertheless, our results from the optimal control model show a clear and rapid change of thermal diffusivity at higher ice temperatures close to the freezing point and a slow change at lower ice temperatures, which is consistent with the experimental data of Reference Chen, Morikawa, Kishi and HashimotoChen and others (2005).
When ice temperature approaches the freezing point, a phase transition (ice crystal melts into water) takes place. The composition of ice (pure ice and gas bubbles) becomes unstable and the corresponding thermal properties (e.g. thermal conductivity, density and heat capacity) inevitably change. In particular, some results have shown that thermal conductivity falls rapidly at higher ice temperatures close to the freezing point (Reference Li, Meng, Yan, Jin and YuLi and others, 1992; Reference Cogné, Andrieu, Laurent, Besson and NocquetCogné and others, 2003; Reference Huang, Li, Liu, Zhao, Guo and JiaHuang and others, 2013b).
Thermal diffusivity depends on thermal conductivity, density and specific heat capacity. When ice temperature approaches the freezing point, density decreases slightly (Reference YenYen, 1981; Reference Leppäranta and ManninenLeppäranta and Manninen, 1988), while thermal conductivity decreases dramatically (Reference Li, Meng, Yan, Jin and YuLi and others, 1992; Reference Cogné, Andrieu, Laurent, Besson and NocquetCogné and others, 2003; Reference Huang, Li, Liu, Zhao, Guo and JiaHuang and others, 2013b) and the specific heat capacity increases (Reference YenYen, 1981). Consequently, the thermal diffusivity determined by these three factors changes and decreases rapidly at higher temperatures.
Our results based on the optimal control model show the clear and rapid change of thermal diffusivity at higher ice temperatures close to the freezing point (Fig. 4). There is excellent agreement between our numerical results and experimental data (Reference Chen, Morikawa, Kishi and HashimotoChen and others, 2005). Figure 4 also demonstrates the ability of our numerical results to overcome limitations experienced by previous numerical studies (Reference YenYen, 1981; Reference Bai, Li, Han and LuBai and others, 2005) at temperatures between - 3 and 0°C. Therefore, the exponential change of the thermal diffusivity of ice at higher temperatures provided by our numerical study is an important supplement to previous numerical results.
It is also important to note that the thermal diffusivity of BHL-A lake ice clearly exceeds previous numerical results (Reference YenYen, 1981; Reference Bai, Li, Han and LuBai and others, 2005) and the experimental data (Reference Chen, Morikawa, Kishi and HashimotoChen and others, 2005) at temperatures between -5 and -15°C (Fig. 4), while comparable to the experimental data by Reference Chen, Morikawa, Kishi and HashimotoChen and others (2005) at temperatures above -5°C. We suggest that the presence of gas bubbles with large size and volume within the ice (Fig. 3a) may explain this result to some extent. Gas has a much greater thermal diffusivity than pure ice. As a result, the thermal diffusivity of ice with more gas bubbles is, in general, higher than pure ice or ice with fewer gas bubbles. In most cases, the size and content of gas bubbles is quite small (Reference Li, Huang, Jia and LeppärantaLi and others, 2011), and their influence on the thermal properties is difficult to examine and is often ignored. Thus, the gas bubbles in the ice may be one of the main factors causing the higher thermal diffusivity compared to previous research. It is also possible that the upper ice layer, where the thermistor cable was located, contained many rachis-shaped gas bubbles.
Conclusions
The ice cover on the QTP is a major component of the environmental and climatic systems of the region on both long and short timescales. In situ measurements suggest that the variations in temperature (of air, ice and water) decrease gradually with increasing depth. Using the optimal control method, we examined the change of the thermal diffusivity of BLH-A lake ice with changing ice temperature. At higher ice temperatures (–3 to 0°C), we find that the thermal diffusivity of the BLH-A lake ice decreases exponentially with increasing ice temperature, and approaches the thermal diffusivity value of fresh water at temperatures close to the freezing point. At lower ice temperatures (–15 to –3°C), thermal diffusivity gradually increases with decreasing ice temperature.
Comparing with previous numerical studies, we show that the thermal diffusivity of BLH-A lake ice, derived using the numerical method, is remarkably consistent with the experimental results. Our result on thermal diffusivity at higher ice temperatures serves as a supplement to previous numerical results that generally cover the low-temperature regimes. The abrupt change of thermal diffusivity at ice temperatures of –3 to 0°C is reasonable based on the experimental data and explains the large difference in thermal diffusivity between ice and water at the freezing point in previous numerical studies.
Although our results are preliminary at this stage, our study of the thermal diffusivity of BLH-A lake ice is helpful to understand the thermal process of lake ice on the QTP. It is also useful for the development of thermodynamic models of fresh water or sea ice in other regions. Further work is necessary in this area, in, for example, the determination of a more accurate model for thermal diffusivity, the quantitative analysis of the effect of gas bubbles on the thermal properties of ice during the growth and decay process, and the improvement of mathematical methods.
Acknowledgements
This study was supported by the National Program on Key Basic Research Project (973 Program) (No. 2012CB026101), the Western Project Program of the Chinese Academy of Sciences (CAS; KZCX2-XB3-19), the National Natural Science Foundation of China (No. 51079021) and the Open Fund of the State Key Laboratory of Frozen Soils Engineering, CAREERI, CAS (No. SKLFSE201202). The study of thermal diffusivity with ice temperature was also supported by ongoing international projects of the Vilho, Yrjö and Kalle Väisälä Fund of the Finnish Academy of Sciences and Letters (No. 2009), and the Norwegian Research Council project AMORA (No. 193592/S30). We also thank the staff at Beiluhe Observation Station for the fieldwork.








