Introduction
The position of tidewater glacier termini is controlled by a variety of factors, including water depth, submarine geomorphology, sedimentation, ice flux into the terminus, rate of calving, and melting of the ice face. The magnitudes and interaction of these various factors are complex (e.g.Reference Van derVeenVan der Veen, 1997) and poorly understood, and the contribution of submarine melting at the terminus remains particularly elusive. Melting has commonly been included implicitly as part of the calving flux, yet the relative magnitude of melting vs calving, and its seasonal variation, may profoundly influence terminus stability. The principal problem in investigating the role of submarine melting is that measurements at an actively calving face are extremely difficult, for obvious reasons.
Some investigators have estimated submarine melting by using relationships developed from field, experimental and analytical studies on icebergs drifting and melting in sea water (Reference Weeks and CampbellWeeks and Campbell, 1973; Reference Powell and MolniaPowell and Molnia, 1989; Reference SyvitskiSyvitski, 1989; Reference Hunter, Powell and LawsonHunter and others,1996). However, such analogies may not accurately reflect the more dynamic process of turbulent convective flow along the terminus face that is driven by discharge of buoyant subglacial water. In a field study of submarine ice melting at Glaciar San Rafael, Chile, Reference Warren, Glasser, Harrison, Winchester, Kerr and RiveraWarren and others (1995) estimated iceberg flux away from the terminus and compared it to the volume flux of ice into the terminus and changes in terminus position. Their results suggested that a significant portion of terminus attrition was due to submarine melting rather than calving, but the uncertainties are large. In another study, Reference Walters, Josberger and DriedgerWalters and others (1988) used heat- and water-balance analyses of oceanographic data to obtain an estimate of submarine melting at the terminus of Columbia Glacier, Alaska, U.S.A. They estimated that melting there was seasonally significant, with melt being about half the iceberg calving flux during the summer.
In late summer 2000 we made nearly simultaneous conductivity, temperature and depth (CTD) and current measurements in the proglacial fjordof LeConte Glacier, Alaska. We also have time-lapse photography of the terminus that spans a 21 month period, and a summer record of fjord water temperature at the terminus. These data are used to analyze heat, fresh- and sea-water balances in the proglacial fjord, and then to estimate submarine melting at the face. Our estimates are compared to analytical expressions for buoyant convective flow and forced convection that have been derived for icebergs drifting in sea water.
Leconte Glacier
LeConte Glacier is located approximately 35 km east of Petersburg, Alaska, and is the Northern Hemisphere’s southernmost tidewater glacier. It mantles the Coast Range Batholith, a complex of resilient tonalite sills and granodiorite plutons. The glacier is approximately 35 km long and has an area of 470 km2. Ice flows from a large accumulation area on the Stikine icefields (elevation range of the accumulation area = 2600–920m, AAR ≈ 0.90; Reference Post and MotykaPost and Motyka, 1995) into a deep, narrow fjord. In fall of 1994, after a 32 year period of terminus stability, it began a rapid 2 km long retreat, before re-stabilizing at a fjord narrows (Fig. 1). Drastic thinning has accompanied the retreat, averaging 1.9 ma−1 over the entire glacier and as much as 25ma−1 near the terminus (1996–2000; Reference Arendt, Echelmeyer, Harrison, Lingle and ValentineArendt and others, 2002).

Fig. 1. Proglacial region of LeConte Glacier showing locations of CTD casts (▲), current measurements (•) (gray dots denote stations used in analysis), time-lapse camera locations (■ ), fjord temperature loggers (×), and zones used in plume discharge calculations. Terminus positions with boundaries seasonal fluctuations shown as cross-hatch.
The near-terminus surface topography is steep, with surface slopes on the order of 10°. Heavy crevassing dominates the lower 8 km of the glacier, with the last 4 km composed mainly of seracs and ice pinnacles. Surface velocities near the terminus steadily increased while the glacier was in retreat, then stabilized at 27md− 1 since 1999 (Reference O’Neel, Echelmeyer and MotykaO’Neel and others, 2001). Terminus activity is high: mass loss via calving and submarine melting is approximately 15 times the entire glacier mass loss due to surface ablation during the year.
Our bathymetric data show that the recently deglaciated fjord is steep-walled and has a maximum proglacial depth of ∼270m below sea level. The terminus is completely grounded, but the majority of the terminal ice lies below sea level. With an average ice-cliff height of 40–60m above the sea surface, the terminus is currently only about 25 m above flotation (Reference O’Neel, Echelmeyer and MotykaO’Neel and others, 2001).
From 1962 to 1994 the average position of the terminus remained constant, but periodic surveys and air photos show that the terminus underwent seasonal fluctuations of up to 300 m, retreating from May to September and then readvancing by the following spring (Reference Motyka, Beget and BowenMotyka and others, 1998). The terminus underwent similar seasonal variations during its calving retreat in 1996 and 1997; similar seasonal fluctuations have been documented elsewhere, most notably at Columbia Glacier (Reference Krimmel and VaughnKrimmel and Vaughn, 1987; Reference KrimmelKrimmel, 2001). Since re-stabilizing in 1998, seasonal fluctuations at LeConte have averaged about 100m and, again, they have exceeded any annual change.
Methods and Basic Results
Terminus position of
To determine seasonal changes in terminus position, we conducted global positioning system (GPS) surveys from a helicopter in May, June and sometimes in late August of each year from 1998 to 2000 (Fig. 1). For reference, the total change along the central flowline was about 140 m from late August to early May in 1998–99, and 90 m in 1999–2000.
In order to track variations throughout the year, we installed a time-lapse camera near the terminus in August 1998; it was moved to a second site in May 1999 (Fig. 1). The images were subsequently analyzed following techniques discussed by Reference O’NeelO’Neel (2000). Controlpoints onbedrock across the channel and in the field of view allowed photogrammetric analysis of the horizontal surface area of the terminus that is visible in each photo frame. Areas were measured from the terminus edge to an up-glacier reference line, about 0.8 km above the seasonal minimum position. The results are displayed in Figure 2 as terminus area vs time. These data are broken into two sections by the camera move, and they were scaled to each other to allow a continuous picture of terminus change from August 1998 to May 2000. A low-frequency filter was applied to these data in order to bring out the long-term seasonal trends (gray line in Fig. 2).

Fig. 2. Horizontal terminus area determined from time-lapse photography (graydots) relative to fixed, up-glacier reference position relative to terminus shown in Figure 1. Filters were applied to data to bring out long-term trends illustrated (black
The terminus retreated during the summer of both years (Figs 1 and 2), with the retreat continuing into fall in both 1998 and 1999, until reaching a minimum in October. It then began advancing, gradually at first and then more rapidly. The rate of advance gradually diminished in late winter, with the terminus reaching a maximum position by late April in 1999 and by early April in 2000.
Proximal fjord water temperatures were measured at a site located about 200m from the south end of the calving terminus during summer 2001 (Fig. 1). Temperature loggers were installed at water depths of 15 and 40 m (the bottom of the fjord at this location). Figure 3 presents results from the lower sensor; data from the upper sensor are nearly identical. We again applied filters to the data to accentuate seasonal trends. Water temperatures rose 4 3 K between 1 June and 4 September 2001, signaling a significant seasonal change in proglacial fjord conditions. We expect that similar changes occur in other years.

Fig. 3. Water temperature vs time at 40 m depth near terminus (gray dots). Filters were applied to data to bring long-term trends illustrated (black line).
CTD and current measurements
On 7 September 2000 we made both CTD and current measurements at a number of locations within 200–500m of the calving face (Fig. 1). Oceanographic parameters were collected using a calibrated Seabird SBE19 CTD instrument, and included temperature, conductivity, pressure (depth), dissolved oxygen (DO), pH and optical backscatter (OBS), which is a measure of suspended sediments. Conductivity was converted to salinity (S). Data from the line of C TD casts nearest the terminus are shown in Figure 4; the other casts had similar features. Casts done in 1999 at similar locations and time of year showed nearly identical features, indicating the 2000 observations are not isolated or anomalous. Four different zones are identifiable in the water column. The first zone extends from the surface to about 30–35 m depth and is characterized by relatively constant t (6°C), comparatively low s (24ppt), high DO (9.0–92 mg L−1), and strong backscatter. All four parameters undergo abrupt changes at 35– 40 m depth (zone 2): t and s increase rapidly, while DO and OBS drop dramatically. These trends continue into zone 3 down to about 100–130 m depth, but at significantly reduced rates. t, s and DO then remain nearly constant to the bottom of the water column at 7.2°C, 27.1 ppt and 7.3 mg L−1, respectively. Backscatterance is also relatively constant except near the bottom, where it increases rapidly in the deepest part of the channel, but not in other casts. This increase in OBS at the sea-floor indicates either an underflow or a nepheloid layer (a layer of water in ocean basins that contains significant amounts of suspended sediments). We favor the latter because temperature and salinity data do not indicate freshwater input at depth.

Fig. 4. Data from CTD casts nearest terminus and closest to current measurements. Four zones were distinguished oceanographic characteristics and are discussed in text.
Near-surface water velocities were measured at 19 near-terminus locations (Fig. 1) with an electromagnetic flow probe. Given the turbulent-flow regime, the accuracy in the direction readings was on the order of ± 10° and ± 5 cm s−1 for velocity. Measurements were made at depth increments of 1.5 m from the surface to 7.6 m. Relative velocity data were converted to absolute values by integrating vessel drift as recorded using GPS. These results are discussed below.
Other observations
Observations show that the maximum position of the terminus coincides with a period when the fjord is usually clogged with icebergs, pan sea ice is prevalent, upwelling at the face is minor or non-existent, and iceberg movement is slow (0.2– 0.5 km d−1). In contrast, during late summer and early fall, upwelling at the face is often strong and icebergs move quickly down-channel (several km d−1). The position and strength of upwelling can fluctuate on several different time-scales: seasonally, daily and even hourly. The longer-term changes appear to be related primarily to changes in air temperature and precipitation (Reference O’Neel, Echelmeyer and MotykaO’Neel and others, 2001). However, large submarine calving events were observed to have strong short-term effects on the strength and position of upwelling.
With regard to conditions during our oceanographic measurements, we note that precipitation had been heavy during the preceding 3 days, averaging 2.4 cm d − 1 at regional weather stations, and air temperatures were relatively warm, 10–15°C. We observed powerful turbulent upwelling along the center of the terminus, which was sufficient to raise the water surface 0.5 m above the ambient level. Standing waves were clearly visible, and icebergs moved rapidly out of the region. The position of upwelling had noticeably changed since a visit 2 days earlier, and its strength had increased. We also observed 2 m deep flutes on the surface of some submarine icebergs calved during our visit, and such flutes had been observed at other times in LeConte Bay.We believe that these flutes were eroded into the submarine ice face by upwelling streams of relatively warm water.
We attempted two other methods of estimating submarine melt, but dismissed both because of inherent methodological problems and unacceptable uncertainties. The first method used visual observations of iceberg flux from the terminus and compared these with measured ice flux into the terminus region (e.g. Reference Warren, Glasser, Harrison, Winchester, Kerr and RiveraWarren and others, 1995). Although the fjord is narrow and has excellent platforms for such observations (Reference MotykaMotyka,1997), we found it was virtually impossible to accurately estimate the volume of iceberg flux. The problems lie with the subjectivity associated with observations of iceberg dimensions, particularly height above water; keeping track of the many icebergs generated by the extremely active terminus; and the inability to monitor calving around the clock. Errors in height are magnified by almost an order of magnitude when extrapolating to total iceberg volume since about 90% of the ice lies below the water-line.
Similar problems beset the second method attempted: consecutive-day photogrammetric surveys of iceberg volume in the proglacial fjord. Uncertainties in photogrammetric models proved intractable because, again, any uncertainty in ice height is magnified when estimating iceberg volume. It also proved difficult to accurately define boundaries between armadas of icebergs on successive air photos because of currents or iceberg disintegration. A further complication arose from the movement of the icebergs between acquisition of stereo photo pairs: motion increased parallax and therefore exaggerated true iceberg height.
Model of Convective Flow In Proglacial Waters
We interpret the combination of lower temperature and salinity, higher dissolved oxygen, and significantly higher backscatter exhibited in zones 1 and 2 as marking the boundary of an overflow plume emanating from the terminus. This plume must consist of a mixture of “warm” sea water and cold (∼0°C) fresh water, such as would be derived from subglacial discharge laden with suspended sediments and from ice melt at the terminus, as no other fresh-water and sediment sources exist this close to the terminus. The rapid transition in zone 2 likely reflects a shear zone between the outflow and the underlying water column. Some residual mixing continues to depths of 130 m or so. Zone 4 appears to consist of undiluted fjord sea water. Its temperature and salinity are similar to that measured in Fredrick Sound, which is the source of sea water entering LeConte Bay. The Stikine River, a major interior continental drainage system, empties into Fredrick Sound just south of LeConte Bay, which probably accounts for the relatively low salinity (27 ppt) of the sound’s waters when compared to average sea water (32–34ppt).
Figure 5 presents our model for convective flow in the proglacial fjord. The main features are based on CTD data, which show that the fjord 200–500m from the terminus is essentially isohaline (salinity = 27.1 ±0.2 ppt) and isothermal (7.2°C) below about 130 m depth. This deep, warm sea water is drawn towards the base of the terminus by buoyant upwelling of subglacial (and englacial) fresh water, possibly aidedby tidal forcing. Our observations of upwelling indicate that subglacial water pressures must be great enough to overcome the hydrostatic pressure of fjord waters. Subglacial discharge is likely driven by “artesian” pressure from influx of surface water at higher elevations that infiltrates to the base of the glacier. Water in subglacial channels is then confined by the ice overburden as it flows to the terminus. Evidence for this effect is basal water pressures near flotation observed in boreholes 12km upstream from the terminus of Columbia Glacier (Reference MeierMeier and others, 1994).

Fig. 5. Model of forced convective flow in proglacial Subglacial discharge, Qsg, carrying heat, Hsg, drives convection, drawing deep saline water (Qs, Hs) towards terminus where the two components mix and turbulently rise along the ice face. The ascending waters melt ice along the face (Qm, Hm), which adds to convection. The turbulent plume reaches the water surface then flows away from the terminus in over- flow plume (Qp, Hp). Dashed lines show possible seasonal geometries of submarine face for conditions of (1) little or no subglacial discharge and melting, and (2) significant sub- marine melting (see text for discussion).
The warm sea water then mixes with and becomes entrained in the cold, upwelling fresh water. This turbulent mixture melts ice as it rises up along the submarine face, which further adds to the forced convection.Whenthis mixed water reaches the surface, it is driven away from the calving face, resulting in a 40 m deep overflow plume. Although some mixing appears to continue down to 130 m, outward flow is primarily contained in the 40 m thick surface layer whose lower shear boundary is marked by the dramatic changes in various oceanographic characteristics (Figs 4 and 5).
Because convection is driven primarily by subglacial discharge in our model, we would expect it to be strongest during the ablation season and weakest during the winter months. Short-term increases in convection due to large amounts of rainfall and/or surface melting would be superimposed on the broader seasonal pattern of convective flow. Melting at the face is a function of both convection and the temperature of incoming sea water, and therefore would tend to be highest in late summer when sea-water temperatures are at their peak (Fig. 3). The geometry of the submarine face is therefore likely to change throughout the year as a function of convection and water temperature (e.g. dashed lines in Fig. 5). Calving observations at LeConte showed that a submarine shelf or foot could periodically exist during spring (Reference MotykaMotyka, 1997), a time when convection and water temperature, and therefore melting, are at a minimum. In contrast, the face may become undercut later in the season (e.g. Reference SyvitskiSyvitski, 1989), when submarine melting increases due to increased convection and higher water temperatures.
Discharge Calculations
Several steps were required to calculate discharge from the observed currents. These include: (1) evaluation of data consistency vs depth, (2) selection of representative data, (3) determination of depth-averaged velocity, and (4) calculation of unit discharge within each flow measurement zone.
Flow consistency within a profile was determined by using the statistics of the velocity and direction measurements. Outliers were eliminated. Typically, three or four readings were used to represent each current-depth profile and to calculate mean velocity, u0, and the representative direction for the upper 7.6 m of the water column. Averaged velocity vectors were then analyzed to identify spatial consistency in these data. It was determined that the data for several stations were too turbulent to provide reliable numbers due to their proximity to the ice margin and the upwelling plume. Stations located along the outer margins of the monitoring grid appeared to be located in gyres, with their flow opposing directions relative to neighboring samples, and therefore were not used. The remaining data were subdivided into nine zones, with one or two current soundings in each (Fig. 1). Based on the zonal boundaries, the total width of the outflow plume was estimated to be about 0.7 km. The resulting near-surface currents and flow directions are given in Table 1. Profile-averaged velocities range from 13 to 52 cm s−1 (Table 1). The direction of flow was generally away from the ice margin; however, large gyres created significant shear flows on the outside of the upwelling and outgoing plume.
Table 1. Summary of discharge calculations

To calculate the average velocity in a 40 m deep column of the overflow plume in each column, we assumed a standard logarithmic profile for shear flow over a smooth boundary layer (Reference Tennekes and LumleyTennekes and Lumley, 1994):
where ub is the “shear velocity”, u is the velocity, k is von Karman’s constant (∼0.4), and z is the distance from the bottom of the flow at 40 m depth. The characteristic shear velocity was determined by evaluating Equation (1) at the surface (z= 40 m) with u = u 0.
We then calculated the column volume discharge, q per unit cross-section of the plume for each zone:

where Zp is the thickness of the plume (40 m). To eliminate effects of turbulent eddies, we converted the directional component to an angle normal to the ice margin. This direction cosine was used to convert q to an ice-front normal discharge. The total zonal discharge (m3 s−1) for the ith zone (Qpi) was determined by multiplying this normal column discharge by the zone width. Values are listed in Table 1.
Zonal-discharge estimates range from 156 to 939 m3 s−1 away from the ice front, with the exception of zone H, which had a flow of 76 m3 s−1 towards the ice (Table 1; Fig. 1). The flow in zone H appeared to be somewhat transient in nature, and may have been affected by nearby eddies. (Water moving along the fjord walls is strongly affected by other eddies, and, as a result, discharge calculations were not extended into these outlying regions.) The total discharge of the outflowing near-surface plume, Qp, was determined by summing the zonal contributions, giving 4044m3 s−1 across the 0.7 kmwide flux band.
Water Balance
The water discharge in the outflowing plume, Q p, has both sea-water, Q s, and fresh-water, Q f, components:
where Q sg and Q m are the subglacial discharge and terminus ice melt, respectively. The fraction of sea water in the overflow plume was determined from the salinity, which is the most accurate parameter available to us for mixing calculations. Salinity of the sea-water component, ss, was taken to be that of the deep fjord water (27.1 ppt), and fresh water was assumed to have sf = 0. We estimate the fraction of sea water (xs) in the plume at a depth z as
where sp is the measured salinity. The total sea-water volume flux in a water column of unit dimension in zone i is then obtained by integration over the 40 m thick plume
Equation (5) was numerically integrated using the shear velocities calculated from u0 and Equation (1), and sp(z) obtained from CTD casts closest to the current measurement sites. The resulting sea-water discharge was multiplied by the width of the zone to give a zonal sea-water discharge,
The total sea-water discharge in the plume is then the sum of the zonal discharges. Table 1 shows that the fraction of sea water is nearly the same in each zone and it accounts for about 89% of the total discharge in the plume, or 3588m3 s−1. To obtain an estimate of the contribution of ice melting to the remaining fresh-water component, which is 11 % of the total, we must first analyze heat balance.
Heat Balance
From conservation of energy, the heat coming into the system via the warm sea water, hs, and via the subglacial water, hsg, must equal the heat leaving the system in the plume, hp, plus the latent heat lost to melting ice, hm:
Here we neglect heat generated by friction and heat lost to the atmosphere, and we assume that hsg = 0 because the ice and subglacial water are at 0°C, which is our reference state. Because the deep water is isothermal and isohaline, we can determine this incoming heat flow from
where C s is the specific heat (4023J kg−1 ˚C −1), ρ s is the density (1022 kg m−3), ts is the temperature of the deep sea water (7.2°C), and where, from conservation of sea water in the fjord, the rate of sea-water inflow near the terminus is assumed to be equal to outflow of sea water in the plume, qs, which was calculated above.
Heat carried away from the terminus by the overflow plume was computed by numerically integrating the following relation within each zone:
using the measured values of mixed-water density and temperature within each zone, and the velocity within the plume calculated from Equation (1). The heat capacity of the plume water was taken to be that of sea water, cs. The contributions from each zone were then added to obtain the total outgoing heat flow, hp (Table 2). The rate of ice melt, qm, is then computed from:
where L is the latent heat of fusion for ice. An adjustment for salt-water melting-point depression of approximately –1.5°C was included in this calculation.
Table 2. Summary of heat flow
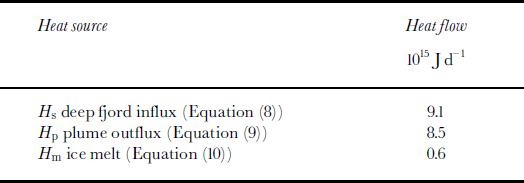
Heat flow is summarized in Table 2. The rate of ice melt determined from Equation (10) is 1.77 6 106 m3 d−1 we. This value was used to complete the water-balance analysis (Equation (3)), giving an estimate for the subglacial discharge, Qsg = 37.6 6 106 m3 d−1 (Table 3). These results show that the total submarine melting is only a small fraction of the overall discharge from the glacier during this late-summer period. However, this melting can be seen to be quite significant when expressed in terms of an average linear melt rate. In water equivalent units, qm corresponds to 12.4md−1 we. of loss over the entire submarine part of the calving face (first entry in Table 4), which has an area of 1.4 6 105 m2.
Table 3. Summary of water volume flow

Table 4. Comparisons of ice-melt rates, Vm (m d–1w.e.) averaged across the submarine terminus face
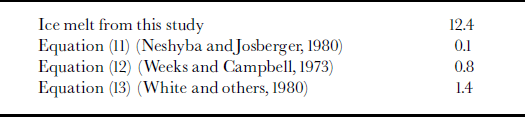
Comparison of Subglacial Discharge and Estimated Surface Water Input
Another estimate of the subglacial discharge at the terminus over this period can be obtained by considering the precipitation and surface melt in the hydrologic basin. LeConte drainage basin has an area of ∼810 km2, of which the glacier covers 470 km2. Limited field measurements indicate that precipitation at the terminus of LeConte Glacier is two or more times larger than that reported by the U.S. National Weather Service at Petersburg and other nearby communities (Reference O’Neel, Echelmeyer and MotykaO’Neel and others, 2001). The regional average rainfall during the 3 days preceding our oceanographic measurements was 2.4 cm d−1. It is improbable that precipitation fell as rain over the entire basin, but it may have rained over a large part of it since temperatures averaged 12°C at nearby sea-level communities during this period. If we assume a lapse rate of –0.007°Cm−1, rain would have fallen up to about 1700 m, or over about 80% of the drainage basin. If we further assume a conservative average rainfall of 4.8 cm d−1 over this area, and that there was no storage of this rainfall, then the resulting discharge at the terminus would have been 31 6 106 m3 d−1. Surface melt also contributed to subglacial discharge, as can be estimated using the same freezing level (1700 m). Assuming a daily ablation rate of 5 cmd−1 we. at lower elevations (Reference O’Neel, Echelmeyer and MotykaO’Neel and others, 2001), the glacier’s area–altitude distribution (Reference Post and MotykaPost and Motyka, 1995), and a linear decrease to zero melt at 1700 m, we estimate that total surface melt was 5 6 106 m3 d−1. Although these estimates are necessarily crude, the total discharge of ∼36 × 106 m3 d−1 is in good agreement with the subglacial discharge calculated in the previous section and listed in Table 3.
Melt Rates from Equations Developed for Icebergs
Other estimates of submarine melting at the terminal ice face can be made using the results of previous empirical and analytical studies of icebergs drifting in sea water. Here we take the ice to be temperate, and the ocean temperature to be t (°C). One such relation, developed by Reference Neshyba and JosbergerNeshyba and Josberger (1980), applies to simple buoyant convection caused by melting at a vertical ice face in stationary sea water:
vm is the melt rate in m a−1. For tidewater glaciers, this equation could apply to situations when there is little or no subglacial discharge at the terminus, such as during mid- to late winter, when fjord water temperatures are likely to be <3°C (Fig. 3). At that time of year, Equation (11) predicts a melt rate of 5 0.03 m d−1, which is quite small. Even in late summer, when there are warmer water temperatures, as shown in Figure 4, it gives melt rates of only 0.12 md−1, which is two orders of magnitude smaller than our heat-balance estimate (Table 4).
Reference Weeks and CampbellWeeks and Campbell (1973) developed another relation for the melting of an iceberg towed at a relative speed of utow (m s−1), which incorporates forced convection and turbulent flow along the submerged iceberg. The melt rate is given by
where lI is a characteristic ice length and vm is in m s−1.
Reference White, Spaulding and GominhoWhite and others (1980) developed a second approximate solution for turbulent flow past tabular icebergs:
Re and Pr are the Reynolds and Prandtl numbers, respectively, k is the thermal conductivity, ρ i is the density of ice, and vm is again in ms−1. At LeConte Glacier, late-summer water temperature is 7°C. We assume that the maximal current in the overflow plume (0.5 m s−1; Table 1) canbe used as a minimum vertical flow rate of water along the ice face, and that the water flows up the average submarine height of the calving face (lI = 200 m). Then Equations (12) and (13) give melting rates of 0.8 and 1.4 md−1, respectively. These values are still substantially less than our estimate of melting based on heat and water balances (Table 4). Streaming velocity along the ice face in Equations (12) and (13) would have to be an order of magnitude larger than that assumed here (0.5 m s−1) to obtain melt rates comparable to our heat-balance-derived estimate.
Terminus Ice Balance
The ice balance at the terminus can be written in terms of water equivalent volume fluxes as
where qc is the calving flux, Qm the melting, Qi n the ice flux into the terminus, and Qout is the rate of change of the terminus position (Reference O’Neel, Echelmeyer and MotykaO’Neel and others, 2001; Table 5). The average ice flux into the terminus during summer 2000 was 3.0 6 106 m3 d−1 based on bathymetry measured in 2000 and terminus ice velocities measured in 1999 (Reference O’Neel, Echelmeyer and MotykaO’Neel and others, 2001) and in 2000 (unpublished data). Our time-lapse photographic record indicates that average late-summer terminus retreat (Qout) was about –0.1 × 106 m3 d−1 we. in both 1998 and 1999. From Equation (14) we thus estimate that calving plus melt is about 3.1 × 106 m3 d−1 we. Our analysis (Tables 3 and 5) indicates that on 7 September 2000, submarine melting alone could account for 57% of this total mass loss. Comparison of average linear rates is even more striking. As noted before, Qm corresponds to 12.4md−1 we. loss over the entire submarine part of the calving face. For comparison, the cross-sectional average ice flow into the terminus (which includes the subaerial face and a total area of 1.9 6 105 m2) is about 16 m d−1 we. This suggests that submarine melting can periodically strongly undercut the subaerial terminus, thus provoking its calving.
Table 5. Ice fluxes (x106m3d−1w.e.) at terminus face

It is interesting to note that melting of the ice face above the water-line is much smaller than this submarine melting. Even with the increased surface area of the calving face, we would expect that the effective subaerial melt rate is on the order of 0.10 md−1.
Discussion
Our estimates of melt and subglacial discharge seem high, but we note that they are similar in relative magnitude to late-summer volume fluxes estimated by Reference Walters, Josberger and DriedgerWalters and others (1988) for Columbia Glacier. The primary sources of uncertainty in our water- and heat-balance estimates are the near-surface current measurements in the overflow plume, the assumed velocity profile, and the flux-band limitation. Temporal and spatial variations in current result in a large cumulative uncertainty in our estimate of plume discharge, which we conservatively estimate to be ±40%. This uncertainty translates directly to the estimates of both melt rate and subglacial discharge. However, even if the lower error bound is assumed, the calculated melt rate and subglacial discharge are still quite large: 1.1 6 106 m3 d−1 (or 6.7 m d−1 over the entire face) and 22.6 6 106 m3 d– 1, respectively.
Our model and analysis for forced convection in the near-terminus fjord suggests that relationships derived for melting of drifting icebergs significantly underestimate submarine melting at glacier termini. We believe this is because the forced convection of warm saline waters along the terminus face, driven by jets of buoyant subglacial water, is a much more complicated and dynamic process than that exemplified by iceberg drift in sea water. The observation of recently calved icebergs with melt-flutes 2 m deep and 2–4 m wavelengths also suggests that localized submarine melting can be quite large.
Our measurements are a snapshot of proglacial conditions at one point in time, in particular when the fjord waters were warm and there was significant, and perhaps exceptional, subglacial discharge from rainfall and surface melt. Our model indicates that submarine melt rates should vary seasonally as a function of fjord water temperature and subglacial discharge. Such melting is likely to be concentrated in zones of strong upwelling
Depending on the geometry of the subglacial discharge plume, submarine melting could substantially undercut the vertical ice cliff and thereby also promote calving of the unsupported ice above (cf. Reference SyvitskiSyvitski, 1989; Reference VieliVieli, 2001). Seasonal embayments in tidewater glacier termini where subglacial discharge occurs may be evidence of this combined effect.
In a recent study, we found that near-terminus ice speeds remained constant (27md−1) during summer 1999, as did ice speed 10 km up-glacier (3.5 md−1) (Reference O’Neel, Echelmeyer and MotykaO’Neel and others, 2001). The near-terminus surface geometry also remained nearly the same, so ice flux into the terminus was nearly constant. Thus either seasonal changes in calving or melting (or both) must account for the seasonal change in terminus position. Even though the data are from different years, the strong correlation of terminus position with changes in fjord water temperature and subglacial hydrology implicates melting of the ice face as a contributing factor. Causative increases in water temperature are due to the influx of warm sea water because fresh-water input is almost entirely from ice, snowmelt and subglacial discharge, which remains at 0°C. However, seasonal increases in subglacial discharge will also be important in forcing convection, and thus in causing submarine melting.
Calving itself may accelerate as a result of seasonal effects (e.g. undercutting by increased submarine melting, or changes in effective basal pressure associated with fluctuations in subglacial discharge (Reference O’NeelO’Neel, 2000)). However, it is likely that submarine melting does contribute directly and indirectly to both short- and long-term changes in terminus position. If so, we suggest that prolonged periods of exceptionally heavy rain, coupled with warm fjord water temperatures, could trigger terminus destabilization of a tidewater glacier. We note that LeConte Glacier began its retreat in fall of 1994, after a long period of exceptionally heavy rain. Also, during its early phases, retreat of Columbia Glacier took place almost entirely during the late summer and early fall (Reference Krimmel and VaughnKrimmel and Vaughn, 1987), a period when subglacial discharge is usually high and fjord sea-water temperatures are at their peak (Reference Walters, Josberger and DriedgerWalters and others, 1988). These observations suggest that calving dynamics control terminus stability rather then upstream processes (Reference Meier and ReehMeier, 1994), although long-term thinning must also play a role (Reference Van derVeenVan der Veen, 1996).
Submarine ablation could also help explain the correlation between annual “calving speed” and water depth found for many grounded tidewater glaciers (e.g. Reference Brown, Meier and PostBrown and others, 1982; Reference Pelto and WarrenPelto and Warren, 1991). The area of the terminus face exposed to submarine melting would increase as a function of water depth since cliff height above water at tidewater calving glaciers appears to remain constant at about 40–60 m, regardless of water depth. It has been noted that the calving-speed–water-depth correlation only holds when annually averaged values are used, and breaks down for shorter time periods (e.g. Reference Van derVeenVan der Veen, 1996). Our model is consistent with this observation, as seasonal changes in convective flow and sea-water temperatures would significantly affect melt rates, but annual melt rates should be approximately the same.
Buoyancy-driven submarine ablation and sea-water temperatures could also help explain the disparity in “calving speeds” between tidewater and lacustrine settings. The lack of a strong density contrast and the generally cooler water temperatures encountered near lacustrine calving glaciers (Reference Warren and KirkbrideWarren and Kirkbride, 2003) would inhibit convection and melting at a sublacustrine face in contrast to submarine environments.
Conclusions
Our analysis indicates that submarine melting can contribute substantially to ice loss at the terminus of a temperate tidewater glacier, especially deep-water systems. In the case of LeConte Glacier in late summer, we found that this melting was at least as significant as calving. Melt rates are related to fjord water temperatures and to forced convection driven by buoyant subglacial discharge. These melt rates are therefore likely to be highest in late summer and after periods of heavy rainfall. We suggest that seasonal fluctuations in the terminus position of tidewater glaciers are directly related to seasonal changes in submarine melting, much as termini of land-terminating glaciers are affected by seasonal changes in surface ablation. Submarine melt will also directly influence calving by undercutting the calving face.
Despite the drawbacks of dealing with iceberg-clogged fjords, we believe that coupling CTD and current measurements with water- and heat-balance analyses is perhaps the only reliable method for estimating submarine melt at tidewater termini. We re-emphasize that this method provides snapshots of discharge and melt at one point in time. Such estimates can be improved by repeat measurements under varying subglacial discharge and fjord conditions, which would provide a range of melt rates under different seasonal conditions.
Acknowledgements
Support for this work was provided by U. S. National Science Foundation grant OPP-9877057. We would like to acknowledge M. Truffer and M. Ferrick for helpful discussions on analysis, and S. O’Neel, J. Johnston, E. Orlikowska and J. Amundson for work on time-lapse photography. Thanks to D. I. Benn, C.R. Warrenandananonymousreviewer for their helpful comments. We also thank D. Lawson for providing the CTD and current meter, and boat captain R. Compton for maneuvering us so close to the terminus.














