Introduction
Many models have already been proposed to describe the motion of snow avalanches (Reference Mellor and VoightMellor, 1978;Reference Perla, Cheng and McClungPerla and others, 1980). In deriving the equations for avalanche motion, the most important factor must be the resistance force exerted during that motion. The resistance force, R, acting on a snow avalanche can be expressed as follows (Salm, 1966):
where the first term, which is independent of the velocity, u, is the Coulomb force, μ is the dry-friction coefficient, Ν is the normal force, the Bu term is the viscous force, and the Cu2 term is the turbulent force. In most earlier numerical simulations of snow avalanches the viscous force, Bu, has been neglected.
We have constructed mini-avalanche systems both in a cold-temperature laboratory and also in a snowfield, and have observed the behaviour of the flowing snow in each situation. This paper presents new results for this type of flowing motion obtained from the mini-avalanche experiments, and discusses the contribution of viscous resistance to snow-avalanche movement.
Measurements
A measured quantity of snow, 5–10 kg in weight, was supplied to an inclined chute within a period of 3–5 s from a fluidized snow feeder. The chute was 5.4 m long and 0.1 m wide, and was inclined at an angle of 40° to the horizontal axis, and is shown schematically in Figure 1. By having one wall of the chute made of glass and the other of wood, it was possible to determine that the decrease in velocity due to wall friction was negligibly small, and less than 10% of the centre velocity of the moving snow. The floor of the chute was covered with sandpaper to give non-slip conditions. The whole experimental system was installed in a cold room, and all the measurements were carried out at a temperature of −15°C. The snow used in the experiments was natural fine-grained snow, which was collected from the suburbs of Sapporo city and kept in a cold room at −10°C for about 10 months before use. The average diameter of the fine-grained snow particles was 0.5 mm.
The movement of individual snow particles, and also the depth of the flowing snow, was viewed and recorded from the side of the chute, with a high-speed video system (NAC HSV-200) which took one picture every two-hundredth of a second. The density of the flowing snow was measured by an electrical capacitance method, a description of which has been given by Reference Maeno and NishimuraMaeno and others (1987). The relative variations in the bulk density of the snow were observed at a height of 0–20 mm above the floor.
Additional experiments were also carried out in a snowfield where the fluidized snow feeder was not available. A weight of between 1.5 and 3 kg of loosened new snow was allowed to flow down an inclined chute, which is 19.8 m long and 0.24 m wide, and whose angle of inclination was 36°. For the first 16.2 m, the floor of the chute was covered with polyethylene film to minimize friction and to achieve higher velocities. The remaining 3.6 m of the chute floor was naturally set up to present a simulation of packed snow conditions. During the data-measurement period the air temperature was in the range −5° to −7°C. The movement of flowing snow was recorded from the side of the chute using a normal-speed video system which was set up 1.0 m above the end of the chute.
Results
Velocities of snow particles
Figure 2 shows a typical example of the variation in depth of snow flow with time for snow flowing down a chute in the low-temperature laboratory. The depth measurements were taken at X = 130 mm, where X is the distance of this position from the end of the chute (Fig. 1). The depth of the snow flow was found to range between 30 and 80 mm. Depth, flow velocity, and total weight of flow were then used to determine the average density of the snow, which was between 200 and 300 kg/m3. Although there were slight changes in the snow-flow depth, due mainly to the mechanism of action of the fluidized snow feeder, the overall profile was substantially reproducible. Figure 2 shows three regions, A, B, and C, which were chosen because the flow depth remained roughly constant or fluctuated around the mean. Figure 3 shows velocity profiles for individual snow particles. It is evident from the results obtained that a mass of flowing snow is composed of two layers: an upper layer in which snow particles move like a rigid body, and a lower layer in which a strong velocity gradient, that is a shear, exists. A similar result was obtained when new snow flowed over a packed snow surface in the field. This is shown in Figure 4.

Fig. 1. Schematic diagram showing the experimental arrangements. A, fluidized-snow feeder; B, chute; C, sandpaper.

Fig. 2. Variation in snow-flow depth with time; results obtained from low-temperature laboratory experiments.
If we regard a snow flow as fluid, then the vertical velocity profile observed in the shear layer can be compared with that derived theoretically. In a Newtonian fluid, shear stress τ is proportional to the velocity gradient, so that
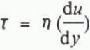
where n is the viscosity of the fluid. Assuming a steady and non-accelerating two-dimensional flow, and substituting Equation (2) into the Navier–Stokes equation, the velocity, u, at height y, can be expressed as follows (Reference Nishimura and MaenoNishimura and Maeno, 1987):
where h is the thickness of the shear layer and U is the velocity at y = h. The data in Figure 3 satisfactorily fit Equation (3) when the constant experimental values which are used are h = 2.5 cm at A, Β and C; U = 3.0 m/s at A, 2.5 m/s at B, and 3.5 m/s at C. Since the velocity profiles shown in Figures 3 and 4 were constructed using data for both the rigid and the shearing regions of the moving snow, the overall snow flow can reasonably be expressed by the Bingham-body model described below, to which model the results obtained on a non-slip horizontal chute in a low-temperature laboratory conform well (Reference Nishimura and MaenoNishimura and Maeno, 1987).
Shear stress in a Bingham-body model is defined as
where τ0 is a yield stress. A Bingham body remains rigid, and no flow takes place, when the shear stress is smaller than τ0; it flows like a Newtonian fluid when the shear stress exceeds τ0. By substituting Equation (4) into the Navier–Stokes equation, and assuming that τ = 0 at y = h, and τ = τ0 at y = H, the theoretical profile is obtained as


Fig. 3. Measured and calculated velocity profiles for flowing snow in the regions A, B, and C in Figure 2.
It is important to note that snow-particle velocities at y = 25 mm become greater with increasing total depth of snow flow, h, for the results represented in Figure 3, although the depth of the shear region, H, is constant, this result does not conflict with Equation (5).
The lower section of Figure 5 shows the variation in bulk density of the snow flow as measured by an electrical capacitance method at a depth of 0–20 mm in the fluidized snow layer, the snow-flow depth is shown in the upper section of the same figure. It will be seen that the internal density of the flow changed considerably with time and that the averaged density of the whole snow flow was in the range of 200–300 kg/m3. In particular, the density varied significantly in the regions marked D and E, although the snow depth in these regions was almost constant. Figure 6 shows that the average snow-flow velocity at E is greater than at D, in spite of the fact that the snow density is lower at E. Taking into account these experimental results, Equation (5) leads to a conclusion that n and τ0 are not constants, but are functions of the internal density of the snow flow.

Fig. 4. Measured and calculated velocity profiles for flowing snow on the surface of packed snow.

Fig. 5. Correlation between snow-flow depth and bulk density of snow at a depth of 0–20 mm.

Fig. 6. Velocity profiles for snow flow in the regions D and E in Figure 5.

Fig. 7. Schematic diagram of the experimental apparatus for generating fluidized snow and for measuring its viscosity.
Discussion
Although the viscous forces term has been neglected in most earlier numerical simulations of snow avalanches, our experimental results, as presented in Figures 3 and 4, suggest that this term should also be taken into account in order to achieve a more realistic and physically reasonable simulation of snow avalanches. The viscosity of fluidized snow has been discussed by Reference Maeno, Nishimura and KanedaMaeno and others (1980) and Reference Dent and LangLang and others (1983), but its dependence on snow density has not previously been studied. We have tried to determine a relationship between the viscosity and the density of fluidized snow. By using our results and substituting the calculated value for kinematic viscosity into an equation for avalanche motion, we hope to be able to simulate the observed avalanche motion in the Shiai-dani region.
Figure 7 shows the experimental apparatus used for generating the fluidized snow and for measuring its viscosity. Snow in the fluidized state was produced by the imposition of a vertical, upward air flow from the bottom of the snow contained in a transparent tube (A) of 75 mm internal diameter. The viscosity of the fluidized snow was then measured with a modified Stormer-type viscometer, Ueshima VR-901, in which the rotor consisted of two paddles with dimensions 18 mm × 7 mm × 0.5 mm. A constant torque was applied to the rotor set in the fluidized snow and the time for 100 revolutions, t100, was measured. The t100 value was converted to the absolute viscosity coefficient by calibration with standard oils. t100 was also measured in the same apparatus without snow in various upward air-flow conditions, giving constant values from which we can assume that the vertical air flow itself does not influence the viscosity of the snow.
The depth, h, of the fluidized snow was recorded from the side of the apparatus using our video system. Assuming that snow density does not change with depth in the fluidized layer, the average density can be calculated. All the measurements were made at a temperature of −15°C. The mean diameters of the snow particles used in the experiments were 0.65 and 0.53 mm. Figure 8 gives the kinematic viscosity values, that is the viscosity coefficient divided by the density, for fluidized snow obtained by the above method. The kinematic viscosity increases with snow density, and varies by approximately two orders of magnitude in the change from 200 to 400 kg/m3, the higher values being obtained for the larger particles.
The avalanche model (Reference Maeno, Naruse and NishimuraMaeno and Nishimura, 1987) used here treats the motion of the centre of mass of an avalanche in a manner similar to that used by Reference Perla, Cheng and McClungPerla and others (1980) and Reference NohguchiNohguchi (1983), but the following improvements were made: velocity-dependence has been considered in the snow-entrainment rate and in the frictional coefficient, the flow route of the avalanche has been computed automatically at every point on a given, real, three-dimensional topography and the viscous resistance force, Bu in Equation (1), which is usually neglected, has been included in the calculation. The friction coefficient, μ, of the Coulomb force was assumed to decrease with velocity as
where μ0 and μ∞ are respectively the friction coefficients at velocity values of zero and infinity, and uμ is a constant. In the following calculation, values of μ0 = 0.5, μ∞ = 0.1, and uμ = 50 m/s were used. The constant, B, is of the order of S = ρv/λ, where S is the area of avalanche bottom and λ, ρ, and v are respectively the depth, density, and kinematic viscosity of the shear layer.
Although the available information about the internal structure of avalanches is very limited, the internal density of the avalanche which occurred on 3 February 1978 in the Shiai-dani region was calculated as 261 kg/m3 (Reference Nishimura, Maeno and KawadaNishimura and others, in press) on the assumption that this avalanche was composed of fluidized snow and dense snow blocks. Thus, using data shown in Figure 8, v is estimated as ranging from 10−6 to 10−4 m2/s. In the following calculations we use a value of 103 kg/s as B, S = 1 × 104 m2, λ = 0.1 m, ρv = 1 × 10−2 Ν s/m2. Values of other parameters used in the calculation are shown in the captions for Figures 9 and 10. The equations of motion

Fig. 8. Kinematic viscosity measurements for fluidized snow.

Fig. 9. Numerical simulations of snow-avalanche motion in the Shiai-dani region, 3 February 1978. Three avalanche paths are calculated from different starting points. Values of parameters selected were as follows: initial avalanche mass, m0 = 1 × 103 kg, density, ρ, depth, D, and width, W, of the fresh snow to be entrained in the avalanche were 150 kg/m3, 2.0 m, and 250 m, respectively; entrainment rate, um = 15 m/s, and α∞ = 0.2; initial velocity, u0 = 3 m/s; Β = 1000 kg/s; C = 5 × 102 kg/m.

Fig. 10. Variations in calculated velocities of snow along the avalanche chute. Values of parameters selected except C are the same as in Figure 9.
were solved by Runge–Kutta method, the time step being selected as 0.1 s. Details of the equation of motion, other selected parameters, and the computation method are to be found in Reference Maeno and NishimuraMaeno and Nishimura (1987).
Figures 9 and 10 show the mathematical simulation of snow-avalanche motion in the Shiai-dani region, where the approximate length and angle of inclination of the valley are respectively about 2000 m and 33°. In Figure 9 the three avalanche paths shown have to be calculated as having different starting points. The unit of mesh is 25 m, the position of the centre of mass of the avalanche is given as a circle every 2 s interval whose radius is proportional to the avalanche mass at that time. Figure 10 shows the change in velocity along the avalanche chute; the solid, broken, and dotted lines are results obtained for C = 5 × l01, 5 × l02, and 5 × 103 kg/m, respectively. Since the avalanche velocity at the observation site, M (Fig. 9), has been calculated to be 22.5 m/s (Nishimura and others, 1988), the broken line, that is the line for C = 5 × 102 kg/m, is considered best to simulate the actual avalanche.
It should be noted that the turbulence coefficient, C, has been set as 5 × 102 kg/m, which is very much smaller than the values most frequently used because the viscous force must be taken into account.
Conclusion
Schaerer and others (1975) have indicated that three zones can be identified in a snow avalanche: a dense flow zone at the base, a middle zone of light flow, and a powder-snow zone. They also reported that the dense-flow snow is usually between 0.5 and 1.2 m deep, and contains the principal mass of the avalanche material. When considering our mini-avalanche experiments, the viscous force originating from momentum transfer in a shear layer must be allowed for, since the internal density of the snow is expected to be rather high in the dense flow region.
In this paper we have described how the kinematic viscosity coefficient of fluidized snow has been obtained experimentally and also how it has been used in the numerical simulation of the Shiai-dani avalanche. Taking into account the viscous term, B, the value of the turbulent resistance, C, was found to be much lower than the values which are most frequently used for it. In the Shiai-dani area many measurements are now being made at the mid-point of the avalanche slope using video cameras, including measurements of movements, impact forces, temperatures, air pressures, winds, and the capture of snow particles. It is hoped that in the near future it will be possible for the various dynamic parameters used in the numerical simulations to be compared with the data collected as a result of these measurements.
Acknowledgements
The authors would like to express their thanks to Drs R. Naruse and H. Narita of the Institute of Low Temperature Science, Hokkaido University, and also to graduate students G. Casassa, K. Kosugi, and K. Akagi for their help in carrying out the experimental measurements described in this paper.














