1. Introduction
The presence of sediments underneath glaciers has far reaching consequences for their dynamics. Where ice overrides a wet subglacial till, enhanced flow velocities may result from pervasive till deformation or sliding at the ice-till interface. Evidence for these mechanisms has been obtained both in the field (Reference Alley, Blankenship, Bentley and RooneyAlley and others, 1986, Reference Alley, Blankenship, Bentley and Rooney1987; Reference Iverson, Hanson, Hooke and JanssonIverson and others, 1995) and in the laboratory (Reference KambKamb, 1991). Their operation generally relies on the water pressure at the base being high, close to the overburden pressure of the ice above. More particularly, there have been attempts to explain ice-stream formation and the (possible) surging behaviour of ice sheets in terms of a feedback instability based on these mechanisms (Reference Fowler and JohnsonFowler and Johnson, 1995, Reference Fowler and Johnson1996; Reference Fowler and SchiaviFowler and Schiavi, 1998). The condition for instability is that the basal-water pressure increases with water flux. A crucial question is then: can drainage over a soft bed exhibit this property?
An earlier theory developed by Reference Walder and FowlerWalder and Fowler (1994) suggests that this is the case. Given the large size of ice sheets, water flow through the till or a subglacial aquifer is usually unable to evacuate all the basal meltwater (Reference ShoemakerShoemaker, 1986; Reference AlleyAlley, 1989); some kind of flow at the ice-till interface is therefore necessary. What Walder and Fowler have demonstrated is that for a soft bed, a network of channels can exist, each with water pressure, pc, increasing with discharge, Q, or equivalent^ effective pressure, NC, decreasing with Q. (Nc =Pi–pc is the difference between the overburden ice pressure and water pressure.) They refer to such channels as "canals". Overall, the subglacial interface is assumed to adopt a similar pressure-flux relationship, because of the distributed nature of the canal network.
Reference Walder and FowlerWalder and Fowler’s (1994) drainage law Nc ∝ Qβ, β ≤ 0, originates from an equilibrium consideration, much in the same way as in the classical theory of ice channels (Reference RothlisbergerRothhsberger, 1972). However, there are two main problems with their canal model: it lacks a detailed description of how the flow interacts with till sediments and also neglects the effect of downstream variation.
In this paper, both of these constituents are shown to be important in governing the channel characteristic, and accordingly we propose an improved model. In comparison to Reference Walder and FowlerWalder and Fowler’s (1994), the theory presented here is more complete, not only because it places emphasis on sediment transport, but also because our governing equations can describe the downstream distribution of effective pressure, as in the classical model. We find that a canal-type drainage law is still possible, but determination of effective pressure now requires knowledge of sediment flux as well as discharge through the channel. This result holds wider implications for the structure of soft-bed drainage systems and the transport of subglacial sediments, and thus also for the long-term dynamics of ice sheets.
The organization of this paper is as follows. We begin by describing our conceptual model (section 2). The governing equations are then introduced and analysed, and we conduct a numerical simulation relevant for an ice sheet (section 3). This is followed by discussion (section 4). Due to the limited space, only the essentials and preliminary results of our investigation will be covered. A detailed theory of canals and further justification of the model will be given elsewhere (Ng, manuscript in preparation).
2. Equilibrium Soft-Bed Channel
Consider a single channel located at the ice-till interface, carrying a discharge Q(s) and sediment volume flux q(s), where s is downstream distance (see Fig. 1a). Initially, let us suppose that the channel cross section is wide and shallow, with a variable aspect ratio (Fig. 1b). This presumption greatly simplifies our mathematical model and is consistent with the solution obtained later. We also impose (in a distributed sense) an inflow of meltwater and sediment to the channel; the supply rates are denoted respectively by M(s) and ε(s). We can therefore mimic the effect of till percolation and adjoining subglacial or englacial tributaries, without having to specify the drainage-network structure.
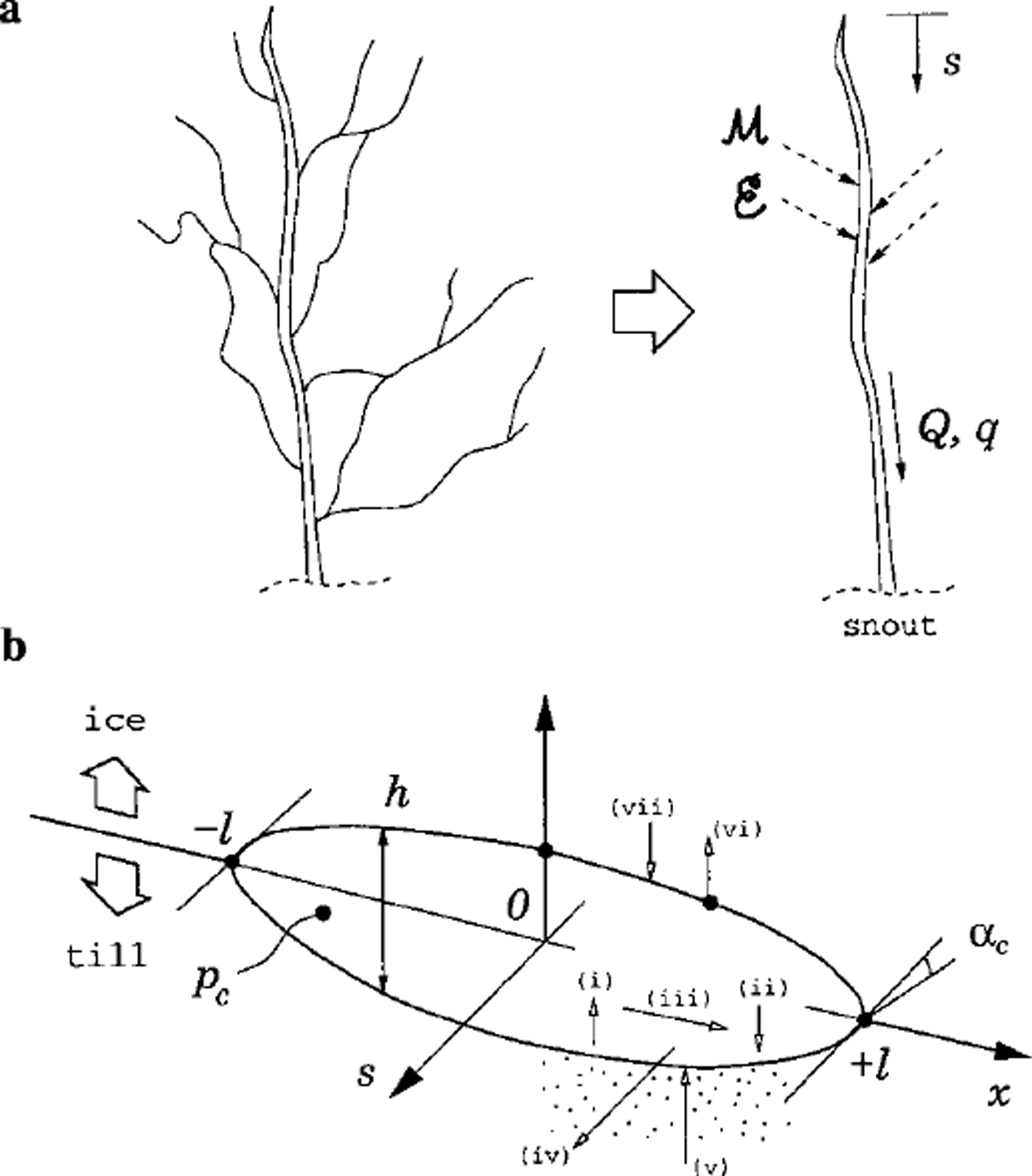
Fig. 1. Idealized model of the subglacial channel and mathematical notations used to characterize its (a) downstream and (b) cross-sectional properties. In (b), the channel boundaries evolve as a result of ( i) erosion, (ii) deposition, (iii) lateral transport, (w) downstream transport of sediment; (v) creep motion of the till; (vi) melting; and (vii) viscous closure of the ice.
Our model is based on the condition of equilibrium drainage, which requires the upper and lower boundaries of the channel to remain stationary. At the roof, this is achieved by a dynamic balance between creep closure and melting of the ice (Reference RothlisbergerRothlisberger, 1972); whereas at the bed, a greater number of constituent processes are involved. These include (1) erosion and (2) deposition of sediment, (3) lateral and (4) downstream sediment transport, and (5) creep motion of till into the channel. Generally, the till would be characterized by a heterogeneous grain-size distribution, so sediment transport may take place as bedload and suspended load as well and this complicates the situation. For convenience, we assume here a till which consists of sufficiently fine-grained, uniform material, such that under typical conditions (when the water flux is not too small), suspension would dominate and bedload may be neglected. A more complete formulation will be described elsewhere (Ng, manuscript in preparation).
The crux of the model is how the mobile bed interacts with the flow and this depends on the relative importance of the five processes listed above (Fig. 1b). Given a wide channel cross section, lateral sediment transport will be negligible because cross-stream gradients are small. The primary balance is then between sediment erosion and deposition. Essentially, this balance dictates the amount of suspended-sediment within the flow section. An analogous situation is found in alluvial river channels (Reference ParkerParker, 1978).
More specifically, lateral transport is relevant only in determining the bed position, but not the flow depth (Ng, manuscript in preparation); and the precise bed-balance is that between net erosion (i.e. erosion minus deposition) and increep of the till. Under typical drainage conditions, the rates of erosion and deposition will be roughly equal and far exceed their difference. Thus, although the creep velocity may be non-zero, its effect on the suspended-sediment concentration locally (within the cross section) will be negligible.
Having said this, the cumulative effect of till creep is important in the downstream direction. This is because suspended sediment is carried along by the flow. Consider the case where tributary supply is absent: ε(s) = 0 (Fig. 1a). At equilibrium, the observed sediment flux at any station along the channel must then be equal to the total creep flux integrated over the channel length, measured from its source to the station. Similarly, the roof is maintained by ice melting and closure, but the meltwater thus generated is advected downstream. The implication is that (at equilibrium) the channel geometry must vary downstream, in such a way that both the water and sediment phases are conserved, while local dynamic balance is maintained. As we shall see, these requirements provide sufficient constraints for determining the entire channel geometry and also the corresponding drainage characteristic. We provide a quantitative description of these ideas in the next section.
3. Mathematical Model
Gross-sectional processes
We define a channel of depth h(x,s) symmetrical in x, where × and s denote respectively its cross-stream and downstream coordinates (Fig. 1b). Hence, if l(s) is the half-width of the channel, then h > 0 in |x| ≤ I and h(x=±1) = 0. In addition we have h/l ≪ 1, since a "wide" cross section has been assumed. In this case, suitable equations to describe the local balances (in x) are
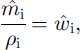
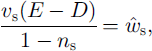
in which ![]() is the melt rate of ice (mass rate per unit width per unit length of channel),
is the melt rate of ice (mass rate per unit width per unit length of channel), ![]() and
and ![]() are respectively the creep-closure velocities at the roof and the bed, and E and D are coefficients which describe the erosion and deposition rates of sediment into/from the flow. Specifically, vs(E - D) represents the rate of net erosion, where vs
is the (constant) grain-settling velocity. The other constants are density of ice Pi and bed porosity ns. Note that Equations (1) and (2) apply in the "upward" direction, normal to the × and
s
axes.
are respectively the creep-closure velocities at the roof and the bed, and E and D are coefficients which describe the erosion and deposition rates of sediment into/from the flow. Specifically, vs(E - D) represents the rate of net erosion, where vs
is the (constant) grain-settling velocity. The other constants are density of ice Pi and bed porosity ns. Note that Equations (1) and (2) apply in the "upward" direction, normal to the × and
s
axes.
Melting is due to the heat dissipated by the turbulent flow. Given that the channel is inclined (downstream) at an angle, αc, and has a water pressure, po, the hydraulic gradient driving the flow is defined by
where ϕ is the water potential, pw is density of water and g is gravitational acceleration. In the following, we use the abbreviation Φ = −dϕ/ds for the hydraulic gradient, and also we introduce the effective channel pressure Nc (= Pi - pc) by rewriting Equation (3) as
in which Ψ is a "basic" hydraulic gradient, imposed externally by topography. A useful approximation is Ψ = pigsinαss, where sinαs is the ice-surface slope (Reference Walder and FowlerWalder and Fowler, 1994). For an ice sheet sin as ∼10−3, so Ψ ∼10 kg m−2 s−2.
Since the flow is wide, the upper and lower boundaries may be considered to be parallel, and its thermomechanics may be summarized by the model
(Reference Fowler and NgFowler and Ng, 1996). Here, r is the total shear stress exerted at the roof and the bed, ![]() is the depth-averaged flow velocity, / is a (constant) friction factor, and L is latent heat. These equations respectively represent a local force balance, a friction parameterization and focal energy balance. Typically / ∼ 0.1, by analogy to rivers (Reference RichardsRichards, 1982). Solving for
is the depth-averaged flow velocity, / is a (constant) friction factor, and L is latent heat. These equations respectively represent a local force balance, a friction parameterization and focal energy balance. Typically / ∼ 0.1, by analogy to rivers (Reference RichardsRichards, 1982). Solving for ![]() and
and ![]() in these equations, we obtain
in these equations, we obtain
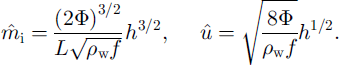
Our prescription for E and D is based on modelling studies in river mechanics. For wide channels, Reference ParkerParker (1978) proposed the expressions
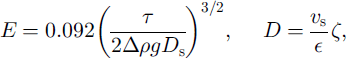
where Δp is the density difference ps - pw (ps is sediment density), and Ds is the representative sediment grain-size. ζ is the total suspended-sediment content-this is the volumetric sediment concentration (a dimensionless ratio) integrated over the vertical flow column, so it is a length with unit m. The eddy diffusivity ∊ is a (focal, depth-averaged) measure of the turbulent-flow intensity; under the parallel-flow formulation as used in Equations (5)-(7), an appropriate expression is

We assume non-linear rheology for both ice and till. If we adopt Glen’s law for ice (see Reference NyeNye, 1953) and the constitutive law proposed by Reference Boulton and HindmarshBoulton and Hindmarsh (1987) for sediment, then approximate relations for the closure rates are
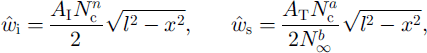
where N∞ is the effective pore-water pressure in the till, far from the channel (see Reference Ng, Wettlaufer, Dash and UntersteinerNg, 1997; Ng and Fowler, submitted). We use the flow-law constants AI = 2 × l0−24 Pa−3 s−1, n = 3, AT = 3 × 10−5 P a b-a s−1, α = 1.33 and b = 1.8.
Various authors have recently questioned the validity of Reference Boulton and HindmarshBoulton and Hindmarsh’s (1987) viscous law for till (e.g. Reference KambKamb, 1991; Reference Iverson, Hooyer and BakerIverson and others, 1998). However, the precise form for ![]() is of minor importance in our model. Notably our concept of downstream sediment conservation (see later) is unaltered so long as the till can deform; also, we argue here that creep effects are generally negligible in the bed balance. To do this, we use conservative estimates together with the fact that Equation (11) 2 is already an upper-bound expression, based on an infinitely deep till (Ng and Fowler, submitted). Suppose N∞ is not too small, say, >0.1 bar. Then taking Ds
= 0.05 mm, vs
= 0.05 ms–1 and the prospective values Nc≈5 bar, h= 0.1m, 1= 10 m, it is easy to show that ws
≪ vsE. Thus henceforth, we neglect the creep term from Equation (2), writing
is of minor importance in our model. Notably our concept of downstream sediment conservation (see later) is unaltered so long as the till can deform; also, we argue here that creep effects are generally negligible in the bed balance. To do this, we use conservative estimates together with the fact that Equation (11) 2 is already an upper-bound expression, based on an infinitely deep till (Ng and Fowler, submitted). Suppose N∞ is not too small, say, >0.1 bar. Then taking Ds
= 0.05 mm, vs
= 0.05 ms–1 and the prospective values Nc≈5 bar, h= 0.1m, 1= 10 m, it is easy to show that ws
≪ vsE. Thus henceforth, we neglect the creep term from Equation (2), writing
(This approximation is justified by our solution later.) Substitution of Equations (5), (8)b (9), (10) and (11)1 into Equations (1) and (12) leads to
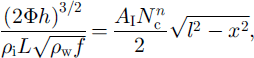
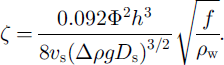
These equations provide the equilibrium depth and sediment distribution across the channel cross section, given Φ, Nc and I (which are functions of a only).
Downstream processes
Following our description in section 2, the downstream increment of discharge Q is due to ice-melting and tributary input; similarly, the increment of suspended-sediment flux, q, is due to sediment entering the channel via creep motion of the till and from tributaries. The corresponding mass-conservation equations are
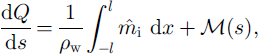
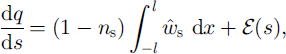
in which ![]() and
and ![]() denote the distributed supply rates (to be prescribed). The appropriate flux definitions are
denote the distributed supply rates (to be prescribed). The appropriate flux definitions are
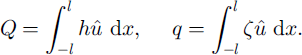
Our model is now completed by substituting for ![]() and ζ from Equations (8), (11)2 (13) and (14). At this point, it is algebraically convenient also to scale the model. This is described next.
and ζ from Equations (8), (11)2 (13) and (14). At this point, it is algebraically convenient also to scale the model. This is described next.
Non-dimensionalization
The head of our channel is taken at s = 0, and its downstream (snout) end at s = s0, where s0 is the total channel length. By choosing the distance scale to be [s] = s0, we can define a suitable dimensionless distance variable
Similarly, let us re-scale the other variables in the model by assigning
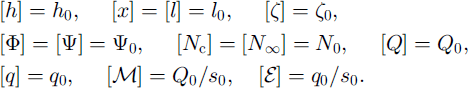
If we impose the scale relations
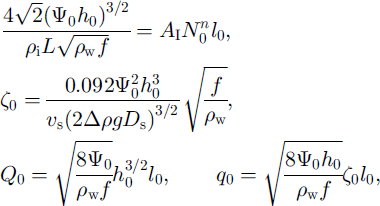
then, on non-dimensionahzing Equations (4) and (13)-(17), we obtain (dropping the asterisks*)
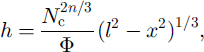
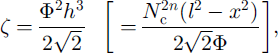
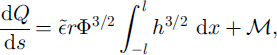
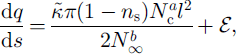
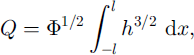
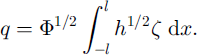
The parameters are given by
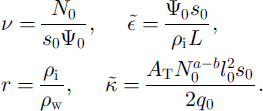
In the following, we assume the constants Pi = 900 kg m−3, Pw = 103 kg m−3, Ps = 2.65 × 103 kg m−3, g = 9.8 m s−2, L = 333.5 kJ k kg–1 " 11, f / / = 0.10.1., ns = 0.3, Ds = 5 × l0−5 m (coarse silt) and vs= 0.05 m s– 1.
The sizes of s
0, h
0, l
0, ζ0, Ψ0, N0, Q
0 and q0 have yet to be specified in the model. For an ice sheet, we can suppose Ψ 0 = 10 kg m–2 s−2, and that a typical drainage length scale is 100 km, i.e. s0 = 105 m. (It follows that ![]() As there are four relations in Equation (20) it is necessary to prescribe two other scales in order to determine the remaining ones. We put N0 = 1 bar, based on borehole measurements on Ice Stream B, Antarctica (Reference Engelhardt and KambEngelhardt and Kamb, 1997). And since
As there are four relations in Equation (20) it is necessary to prescribe two other scales in order to determine the remaining ones. We put N0 = 1 bar, based on borehole measurements on Ice Stream B, Antarctica (Reference Engelhardt and KambEngelhardt and Kamb, 1997). And since ![]() it is natural to ensure in Equation (24) that
it is natural to ensure in Equation (24) that ![]() , by choosing an appropriate value of
, by choosing an appropriate value of ![]() . Strictly speaking, this scale can be estimated from the basal-ice-melt rate and channel spacing, but the specification of these is difficult (particularly for ice sheets). Alternatively, one can simply prescribe Q0 to be the (expected) outlet discharge. Here we use the nominal value Q0
= 1 m3 s−1; then, the remaining scales are
. Strictly speaking, this scale can be estimated from the basal-ice-melt rate and channel spacing, but the specification of these is difficult (particularly for ice sheets). Alternatively, one can simply prescribe Q0 to be the (expected) outlet discharge. Here we use the nominal value Q0
= 1 m3 s−1; then, the remaining scales are
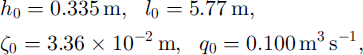
and the corresponding parameters are
Evidently, discharge contribution from roof melting is going to be negligible (since ε ≪ 1, independent of the choice of N0
and Q0), whereas the effect of till creep can be quite significant (since ![]() in Equation (25); remember however, that
in Equation (25); remember however, that ![]() is an upper bound estimate and depends on N0
and Q0). These inferences are unaffected if we had chosen s0 according to the ice-sheet length scale (e.g. 103 km) instead.
is an upper bound estimate and depends on N0
and Q0). These inferences are unaffected if we had chosen s0 according to the ice-sheet length scale (e.g. 103 km) instead.
The reduced model
By eliminating h and ζ from Equations (21)-(27), we obtain, after some algebra,
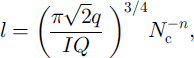
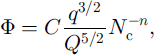
and the following coupled model for Q, q and Nc :
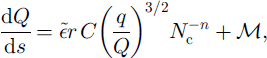
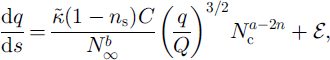
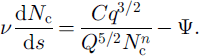
Here the constants are ![]() (by numerical integration) and C = π 5 / 2 / 2 1 / 4 / 3 / 2 ≪ 10.2.
(by numerical integration) and C = π 5 / 2 / 2 1 / 4 / 3 / 2 ≪ 10.2.
Equation (35) describes the effective pressure distribution Nc(s) and is our drainage equation for a soft bed. This is supplemented by Equations (33) and (34) which provide recipes for Q and q. Note that, if in our derivation we had neglected the sediment processes and imposed a cylindrical channel geometry (by putting h = I, dimensionally), then we would obtain
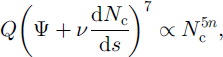
which is essentially the classical result (cf Reference RothlisbergerRöthlisberger, 1972; equation (11)).
Given suitable boundary conditions, Equations (33)-(35) may be solved. We put Ψ = 1, and for simplicity we assume ![]() and
and ![]() to be constants. These supply rates can be estimated from the typical discharge values expected at the snout. For instance, setting
to be constants. These supply rates can be estimated from the typical discharge values expected at the snout. For instance, setting ![]() (which gives Q(snout) ≈ 1 m3s−1 ) is consistent with our current model scaling, and as a first estimate, we can choose
(which gives Q(snout) ≈ 1 m3s−1 ) is consistent with our current model scaling, and as a first estimate, we can choose ![]() , such that the
, such that the ![]() ratio corresponds to a (influx) suspended-sediment concentration of tens of grams per litre, typical of glacier-fed streams (Reference LawsonLawson, 1993). In general, the actual concentration in the channel would increase with downstream distance and exceed this, due to the effect of till creep (since
ratio corresponds to a (influx) suspended-sediment concentration of tens of grams per litre, typical of glacier-fed streams (Reference LawsonLawson, 1993). In general, the actual concentration in the channel would increase with downstream distance and exceed this, due to the effect of till creep (since ![]() Our simulation results later confirm this, with the outflow-sediment load predicted at roughly 100 g IT1, which is still within the plausible range.
Our simulation results later confirm this, with the outflow-sediment load predicted at roughly 100 g IT1, which is still within the plausible range.
We also specify a nominal (dimensional) value N∞ = lbar. The parameters in Equations (33) and (34) are then ![]() and
and ![]() (an upper bound estimate). These values indicate that Q is an increasing function of s, with &Q/&S ≪ M, whereas q(s) also increases monotonically, but not necessarily linearly.
(an upper bound estimate). These values indicate that Q is an increasing function of s, with &Q/&S ≪ M, whereas q(s) also increases monotonically, but not necessarily linearly.
The solution for Nc is more complicated, v ≪ 1 suggests that Equation (35) may be approximated as
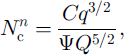
which indicates a canal-type characteristic, i.e. Nc α Q3, where (5 = - 5 / 2 n ≤ 0 (and (5 = - 5 / 6 with n = 3). However, this is a singular approximation because v multiplies into a first-order derivative. There will be a boundary layer (of thickness O(y) corresponding to a distance of 10 km) in which effective pressure gradients are significant, and this occurs at the head of the stream. Nevertheless, the canal drainage law (Equation (37)) is applicable outside this boundary layer, sufficiently far downstream that pressure gradients are negligible.
Last, we discuss the form of the boundary conditions at s = 0. Care is required here in order to avoid the righthand terms in Equations (33)-(35) becoming singular, which will occur if Nc = 0 or Q = 0 there. Our prescription is based on the following consideration. Although the channel has its top end defined at s = 0, we envisage that it is connected to (Darcy) drainage in the till via some kind of channel filaments, in which the water flux is small but non-Zero- hence, Q should not vanish there, or Q(0) > 0. On the other hand we specify q(0) = 0, by assuming that the incipient discharge would be too small to sustain sediment transport, i.e. the flow stress at the bed ( ≪ τ / 2 ) there is below its critical value for sediment entrainment. As a result, we can also expect these incipient channels to behave essentially like hard-bed channels, with Nc directly related to Q (Reference RothlisbergerRöthlisberger, 1972). Therefore Ac(0) should be relatively small (but non-zero, since that would imply flotation of the ice), and a natural choice is Ac(0) = N∞. Given these boundary conditions, a local analysis of the model shows that the solutions are well-behaved, and in particular neither Nc nor Q would vanish in 0 ≤ S ≤ 1.
Numerical solution
Equations (33)-(35) have been solved by using a simple Euler predictor-corrector algorithm. This algorithm uses finite difference and steps forwards in s from s = 0, where we specify the dimensionless initial conditions Q(0) = 10–2 (corresponding to 0.01 m3 s−1, ∼ ∼Q(snout)/100), q(0) = 0, and Ac(0) = 1 (corresponding to lbar). As a trial simulation, we employ the scales and parameters given in Equations (29) and (30), and also the model constants M = 1, ε = 0.1, Ψ = 1.
Figure 2 shows the computed results plotted in dimensioned units. As expected, we see the downstream increase of Q and q (Fig. 2a) and the boundary-layer behaviour in Nc (Fig. 2b). The canal solution in Equation (37) has been included for comparison, and is found to be a good approximation in s > 30 km, where the predicted effective pressure is NC ≪ 1.5 bar. We have also investigated the effect of varying Ac(0) in the simulation. Downstream in the "canal" region, Nc is insensitive to its boundary value at the stream head (Fig. 2c).
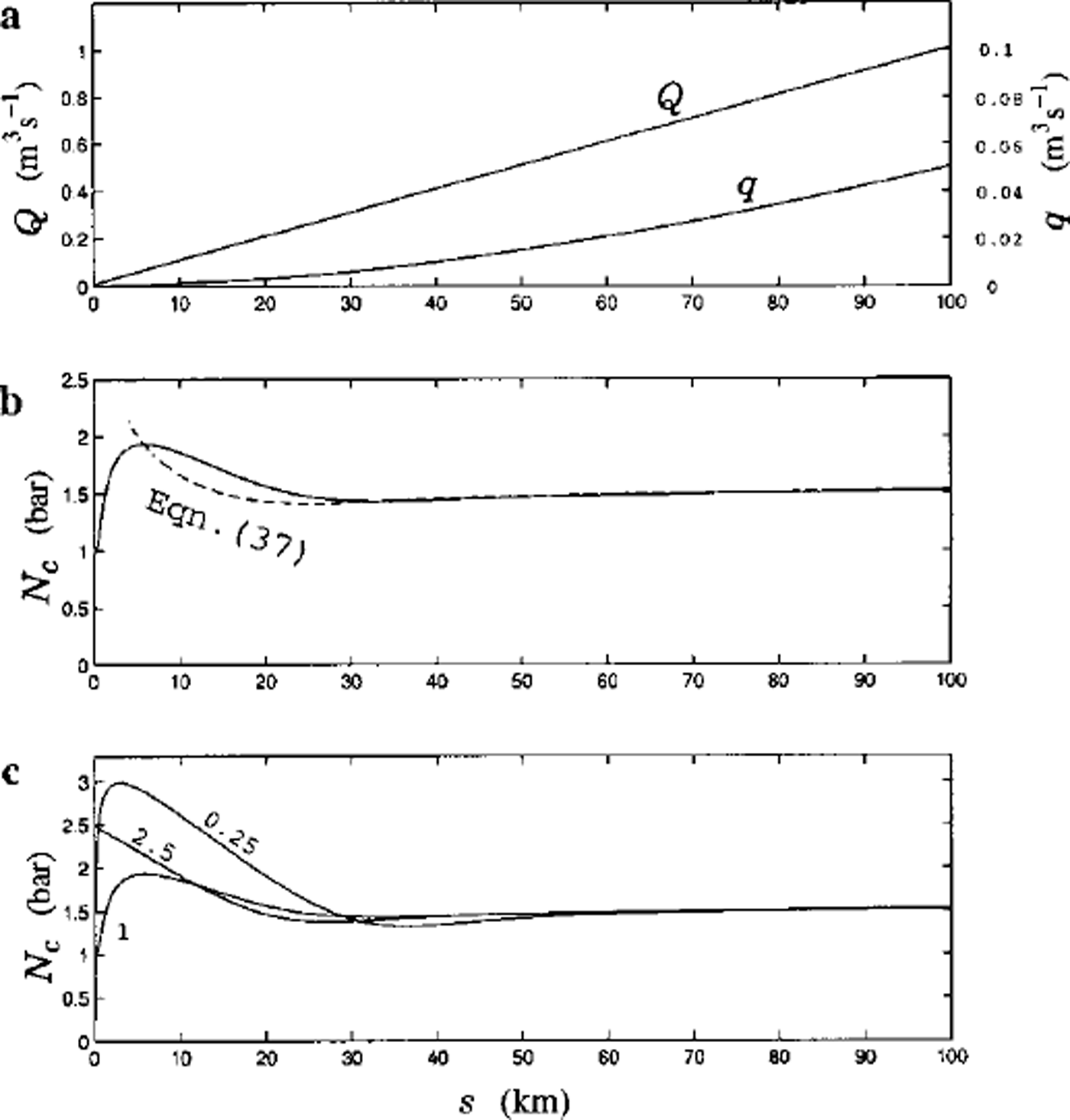
Fig. 2. (a) Computed discharge, Q, and sediment flux, q, and (b) computed effective channel pressure, Nc, as functions of downstream distance, s. Dashed line represents Nc as given by Equation (37). (c) Sensitivity of the simulated Nc(s) to its upstream boundary condition. Test values are Ac(0) = 0.25,1 (as in (b)), and 2.5 bar.
Figure 3 shows other results derived from Figure 2a and b. The suspended-sediment load in g L–1 is calculated by evaluating psq/Q (Fig. 3a), and is found to be of the order of 100 g L−1, rather high in the plausible range of values. This is due to the large (upper-bound) value of ![]() used in the simulation. For example, reducing k by a factor often would reduce the sediment load at the outlet to about 50 g L–1. In addition, we have calculated the depth and width variations of the channel h(x=0,s) and l(s) via Equations (22) and (31) (see Fig. 3b and c). In general h ≪ 21, so the channel adopts a wide cross section, consistent with model assumptions. (h appears to blow up close to s = 0. This spurious feature is due to the neglect of bedload transport in the model, and does not affect the canal approximation downstream. Further examination of this is given by Ng (manuscript in preparation).) At the snout, the channel cross section is approximately 5 m across by 0.45 m deep.
used in the simulation. For example, reducing k by a factor often would reduce the sediment load at the outlet to about 50 g L–1. In addition, we have calculated the depth and width variations of the channel h(x=0,s) and l(s) via Equations (22) and (31) (see Fig. 3b and c). In general h ≪ 21, so the channel adopts a wide cross section, consistent with model assumptions. (h appears to blow up close to s = 0. This spurious feature is due to the neglect of bedload transport in the model, and does not affect the canal approximation downstream. Further examination of this is given by Ng (manuscript in preparation).) At the snout, the channel cross section is approximately 5 m across by 0.45 m deep.
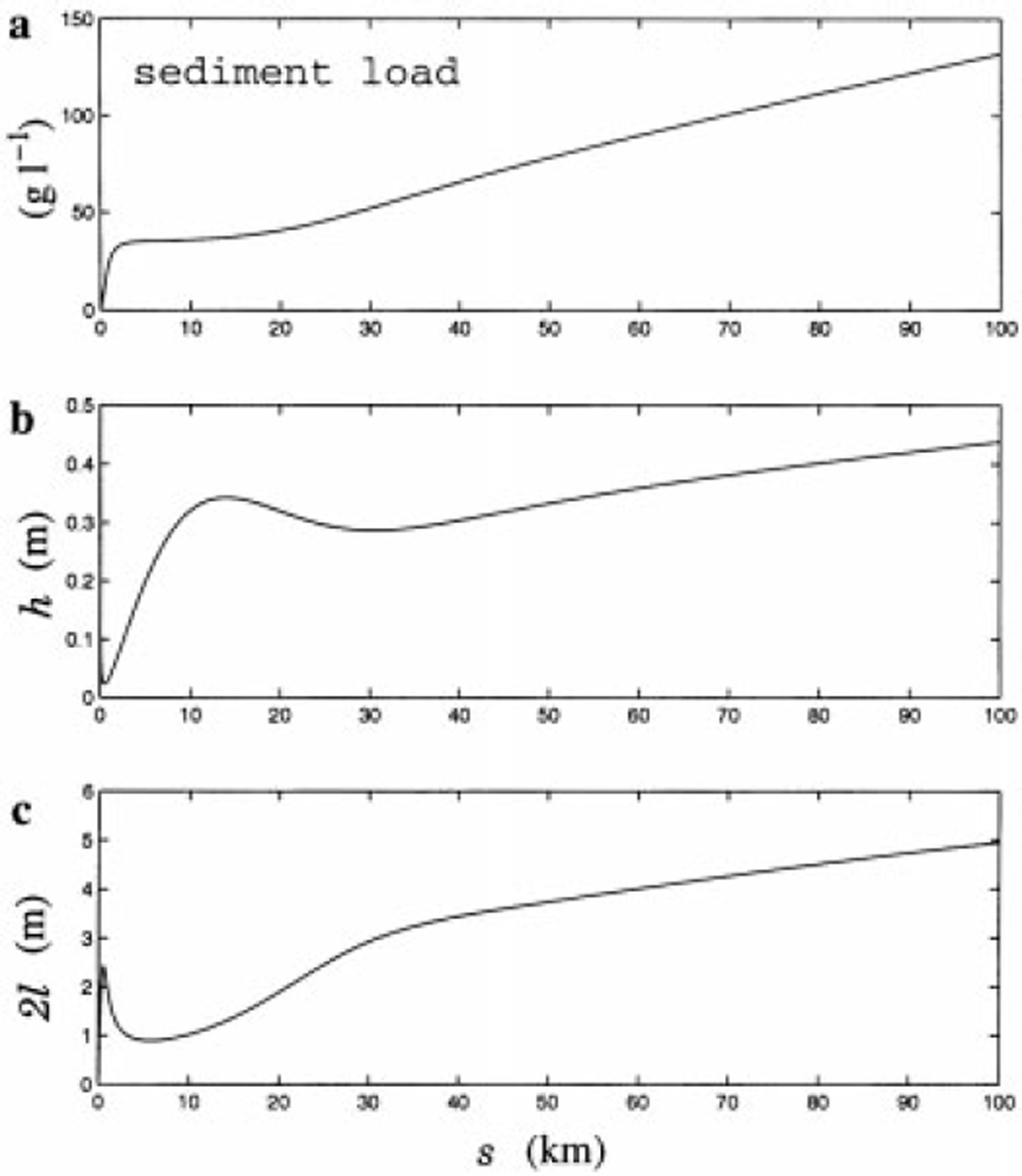
Fig. 3. Downstream variations of (a) sediment load, (b) channel depth h(× = 0,s) and (c) total channel width 2 × l(s), corresponding to the simulation in Figure 2a and b.
Finally, our solution (and Equation (37)) indicates a nonzero value of Nc at s = 100 km. This is significant because if the ice thickness (Hi) vanishes at the snout then the channel water pressure (pc) would become negative (!) there. In practice, we suppose open-channel flow occurs when Pc = 0, so our model predicts that pressurized flow would terminate some distance back from the snout. The position of this transition s = sco is given approximately by the relation
For our model ice sheet, Hi(Sco) is about 20 m.
4. Discussion
The present work furthers our understanding of soft-bed subglacial channels and exposes some of the limitations of previous models. Where ice overrides till, the coupled flow of water and sediment is inevitable, and any realistic theory of soft-bed drainage must take this into account. We have developed a model which supersedes that of Reference Walder and FowlerWalder and Fowler (1994) and our findings support their conclusion that sediment-floored channels can exhibit canal-type characteristics, with effective pressure inversely related to discharge; the exact relation depends on the channel sediment flux. This behaviour, summarized by Equation (37), occurs where effective pressure gradients are small and is independent of the value assumed for the constant n in Glen’s flow law, as long as n > 0.
Regarding downstream variation, it is interesting to compare the predictions of our theory and the classical theory (Reference RothlisbergerRothhsberger, 1972), where sediment processes are ruled out altogether and restriction of a cylindrical-channel cross section is enforced. The main difference lies in the form of the respective drainage equations. Written in the form of Equation (35) (which applies for a canal), Equation (36) (for an R channel) would have a positive power of Nc appearing in the numerator of the first righthand term. The implication is that Nc can decrease to a small value only with negative slope (dNc/ds ≤ 0). For instance, taking Nc (snout) = 0 (the boundary condition used by Röthlisberger) and a linearly increasing distribution for Q, it is straightforward to confirm this by integrating Equation (36) numerically. In this case, the boundary layer in Nc occurs near the channel outlet, with Nc reaching a near-constant (high) value upstream. This is essentially the opposite result to that for the canal, where Nc may assume any non-zero (but presumably low) till value at the stream head because the boundary layer occurs there (see Fig. 2b and c); in this case however, Nc cannot vanish at the outlet, so the canal model actually predicts the position of the closed/open-channel flow transition near the snout. (Although Reference RothlisbergerRothlisberger’s (1972) model does allow the possibility of open-channel flow under some conditions, he defined the channel outlet to be situated where the flow transition takes place, without specifying its position relative to the snout; see p. 178 and 185.)
Our theory can be extended to a more general description for soft-bed drainage. Notably, it provides a starting point for investigating how the canals would couple to each other and to other forms of drainage. Currently, the quantities Nc(0), Q(0), M(s) and ε(s) are poorly constrained in the model. The question of how to specify these is intimately related to the problem of determining the architecture of the drainage network.
For instance, one can consider a network in which the tributary channels feeding our main channel are themselves sustained by finer tributaries, and so on; each level of the hierarchy may be described by our ingredient model. In building a model for the entire drainage system, the four quantities in question would then appear as unknowns, instead of being externally prescribed. In particular, Nc(0) and Q(0) would describe how the canals are connected to the till via incipient channels, and in isolated cases, to englacial sources; M and ε would describe the network structure (channel spacing and order of linkage). Model solution determines the system architecture, the basal-water-pressure distribution, and in addition, the rate at which till sediments are depleted by drainage. The last of these is relevant to the sediment budget and is clearly important in the long term, as changes of till thickness could have a drastic effect on the nature of basal-ice dynamics. This generalized model awaits further investigation.
Acknowledgements
The author thanks St. John’s College, University of Oxford for a Junior Research Fellowship position. A. C. Fowler continues to be a constant source of inspiration.




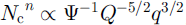 where N
where N


