Article contents
On the chordwise lift distribution at the centre of swept wings
Published online by Cambridge University Press: 07 June 2016
Summary
The present note deals with the peculiarities of the lift distribution on swept wings. The influence of the angle of sweep is expected to be greatest in its effect on the chordwise lift distribution at the centre section of the wing. It is assumed that the essential characteristics of this chordwise lift distribution are predominantly determined by the special configuration of the bound vortices and not so much by the trailing vortices. In calculating the downwash, induced by a continuous chordwise distribution of swept vortex lines of infinite span, it is found that the downwash at the centre line is to be expected to differ from its two-dimensional form mainly by a term proportional to the local vortex strength. Solutions of this simplified downwash equation have been obtained. They differ from the ordinary fiat-plate distribution only in the exponent which instead of 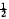 becomes
becomes 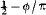 .It is suggested that this type of function is more appropriate for the centre-section of swept wings and that it may replace the ordinary flat-plate distribution in all those cases where the lifting surface is swept.
.It is suggested that this type of function is more appropriate for the centre-section of swept wings and that it may replace the ordinary flat-plate distribution in all those cases where the lifting surface is swept.
- Type
- Research Article
- Information
- Copyright
- Copyright © Royal Aeronautical Society. 1950
References
- 5
- Cited by


