Article contents
Approximation algorithms in combinatorial scientific computing
Published online by Cambridge University Press: 14 June 2019
Abstract
We survey recent work on approximation algorithms for computing degree-constrained subgraphs in graphs and their applications in combinatorial scientific computing. The problems we consider include maximization versions of cardinality matching, edge-weighted matching, vertex-weighted matching and edge-weighted 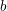 $b$-matching, and minimization versions of weighted edge cover and
$b$-matching, and minimization versions of weighted edge cover and 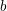 $b$-edge cover. Exact algorithms for these problems are impractical for massive graphs with several millions of edges. For each problem we discuss theoretical foundations, the design of several linear or near-linear time approximation algorithms, their implementations on serial and parallel computers, and applications. Our focus is on practical algorithms that yield good performance on modern computer architectures with multiple threads and interconnected processors. We also include information about the software available for these problems.
$b$-edge cover. Exact algorithms for these problems are impractical for massive graphs with several millions of edges. For each problem we discuss theoretical foundations, the design of several linear or near-linear time approximation algorithms, their implementations on serial and parallel computers, and applications. Our focus is on practical algorithms that yield good performance on modern computer architectures with multiple threads and interconnected processors. We also include information about the software available for these problems.
- Type
- Research Article
- Information
- Copyright
- © Cambridge University Press, 2019
Footnotes
The work of the first two authors was supported in part by US NSF grant CCF-1637534; the US Department of Energy through grant DE-FG02-13ER26135; and the Exascale Computing Project (17-SC-20-SC), a collaborative effort of the DOE Office of Science and the NNSA.
References
REFERENCES 2
- 9
- Cited by




