1 Introduction

In July 2012, the CMS and Atlas collaborations working at the Large Hadron Collider (LHC) at CERN in Geneva, Switzerland jointly announced [Reference Aad, Abajyan and Abbott1],[Reference Chatrchyan, Khachatryan and Sirunyan2] the detection of a scalar boson of mass roughly 125 GeV decaying into two photons and exhibiting the properties of the Higgs boson, the particle remnant of the electroweak symmetry-breaking mechanism of the Standard Model (SM) of particle physics. For their theoretical work describing this mechanism, P. Higgs and F. Englert were jointly awarded the 2013 Nobel Prize in Physics. This prize was really all about the role of symmetry, its form and its realization, in the electroweak interactions. Symmetry has also played a crucial role in the development of the theory of strong interactions, Quantum Chromodynamics (QCD), the other component of the Standard Model. In fact, one might argue that the deeper understanding of symmetry in many ways underlies much of the physics of the past century. In this Element we discuss the role symmetry played leading to the construction of the SM. The treatment makes no real attempt to strictly follow the chronological development of the SM. However, we try to indicate some of the important hurdles encountered along the way and how they were overcome. In addition, this approach gives us the opportunity to introduce in a natural fashion some of the basic concepts that underlie the Standard Model. We then briefly discuss some of the model’s successes and limitations as well as some open questions that appear to require extensions beyond the model.

The modern view of the role of symmetry originated with Albert Einstein, whose general theory of relativity [Reference Einstein3],[Reference Einstein4] related gravitational interactions to the principle of general coordinate invariance. The use of a symmetry principle as the primary feature of nature that constrains and even dictates the allowable dynamical laws lies at the heart of the Standard Model. The Standard Model is designed to describe the strong, weak and electromagnetic interactions while treating gravity as a classical (flat) background. Thus it must respect the principles of special relativity. In addition, the dynamics needs to conform to the postulates of quantum theory. Since special relativity allows for particle pair production, any formulation must be able to account for arbitrary and varying numbers of particles. The only consistent way to achieve this is using a relativistic quantum field theory, with the textbook of Peskin and Schroeder [Reference Peskin and Schroeder5] being one commonly used for reference. Here the particle modes arise as excitations of operator quantum fields ${\zeta }_a\left(x\right)$ , labeled by the space-time point $x^{\mu }$ and an index $a$ that distinguishes the various fields. (Appendix A.1 details the notations and convention employed.) The dynamics is encoded within the action functional

$S\left[\zeta \right]=\int d^{4}xL\left(x\right),$(1.1)

where the local Lagrangian density $L\left(x\right)$ is a function of the quantum fields and their space-time derivatives. This Lagrangian will also depend on various parameters. To fully define the theory, these parameters need to be fixed by certain normalization conditions. Using the Lagrangian, one extracts the various Feynman rules that can be employed in perturbative calculations. Some of the radiative corrections that arise from Feynman graphs containing closed loops can be included by defining scale-dependent (running) couplings to replace the couplings appearing in the Lagrangian. The form of the running coupling can be most easily secured using the renormalization group [Reference Peskin and Schroeder5–Reference Wilson and Kogut9].

2 Wigner–Weyl Realization of Global Symmetries

Symmetries are represented by transformations of the fields that leave the action functional invariant. Included within this class are the space-time Poincaré transformations (space-time translations, spatial rotations and Lorentz boosts) of special relativity.

In addition to space-time symmetries, the action is constructed to be invariant under various transformations of the fields that depend on continuous parameters, $\left\{{\omega }_i\right\}$ , which do not alter the space-time point. When the parameters themselves are independent of space-time, such symmetries are referred to as continuous global internal symmetries. In this case, a symmetry of the action is necessarily a symmetry of the Lagrangian density. Wigner’s theorem [Reference Wigner10] then dictates that these symmetries can be implemented on the Hilbert space of states by unitary operators, $U\left(\right\{{\omega }_i\left\}\right)$ , depending on parameters characterizing the transformation. Here $i=1,\dots ,n$ , with $n$ being the number of group parameters. The invariance is then the statement that the Lagrangian density commutes with the unitary operator $U$ :

$U^{-1}\left(\right\{{\omega }_i\left\}\right)L\left(x\right)U\left(\right\{{\omega }_i\left\}\right)=L\left(x\right).$(2.1)

We shall primarily focus on continuous global transformations that form a Lie group. (See, for example, the text by H. Georgi [Reference Georgi11].)

Although the Lagrangian $L$ is constructed to be invariant under a certain set of transformations, the quantum fields will, in general, transform among themselves under these same transformations. We shall concentrate on quantum fields ${\zeta }_a\left(x\right)$ that transform irreducibly under the symmetry. The concept of irreducibility is simply that, under the transformation, a set of fields ${\zeta }_a$ will go into a linear combination of themselves. That is, one has

$U^{-1}\left(\right\{{\omega }_i\left\}\right){\zeta }_a\left(x\right)U\left(\right\{{\omega }_i\left\}\right)=R_{ab}\left(\right\{{\omega }_i\left\}\right){\zeta }_b\left(x\right).$(2.2)

Here $R_{ab}\left(\right\{{\omega }_i\left\}\right)$ are matrix elements of the representation matrices describing the given symmetry transformation.

Because we are dealing with continuous symmetries, it is possible and convenient to restrict attention to infinitesimal transformations. Finite transformations can then be obtained by simply compounding these infinitesimal transformations using the group property. For an infinitesimal transformation characterized by a set of dimensionless parameters $\left\{\delta {\omega }_i\right\}$ , with $|\delta {\omega }_i|\ll 1$ , one can write the operator $U\left(\right\{\delta {\omega }_i\left\}\right)$ as

$U\left(\right\{\delta a_i\left\}\right)=1+i\delta {\omega }_i{G}_i.$(2.3)

The operators $G_i$ are known as the generators of the transformation. For each independent infinitesimal parameter $\delta {\omega }_i$ there is one generator associated with it. With no loss of generality, one can take these parameters to be real. The unitarity of the $U\left(\right\{\delta {\omega }_i\left\}\right)$ then dictates that the generators $G_i$ are Hermitian: $G_i=G_i^{†}$ . The group composition property associated with the symmetry transformations is encoded in the Lie algebra obeyed by the generators and characterized by a set of structure constants $c_{ijk}$ so that

$[G_i,G_j]=i{c}_{ijk}{G}_k.$(2.4)

The structure constants are obviously antisymmetric in $i$ and $j$ . Moreover, by suitably defining the generator basis, they can also be made totally antisymmetric in $i,j$ and $k$ . For infinitesimal transformations, the representation matrices $R$ have a similar decomposition to Eq. (2.3) involving Hermitian matrices ${\tau }_i$ :

$R_{ab}\left(\right\{\delta {\omega }_i\left\}\right)={\delta }_{ab}+i\delta {\omega }_i({\tau }_i{)}_{ab}.$(2.5)

These matrices provide a representation for the generators $G_i$ and thus obey Eq. (2.4). Using Eqs. (2.4) and (2.5). It is easy to check that the transformation law for the fields ${\zeta }_{\alpha }$ , given in Eq. (2.2), specifies the commutator of the generators $G_i$ with the quantum fields being

$[G_i,{\zeta }_a(x\left)\right]=-\left({\tau }_i{)}_{ab}{\zeta }_b\right(x).$(2.6)

A general consequence of having a Lagrangian density $L$ invariant under some global symmetry group is that associated with each of the independent symmetry transformations there exists a conserved operator (Noether) current [Reference Noether12] and a related time-independent operator charge. In fact, the operator charges are just the generators $G_i$ , which for any given theory can be expressed in terms of the quantum fields ${\zeta }_a$ . The Noether current is given by

$J_i^{\mu }\left(x\right)=\frac{\partial L}{\partial {\partial }_{\mu }{\zeta }_a\left(x\right)}\frac{1}{i}\left({\tau }_i{)}_{ab}{\zeta }_b\right(x),$(2.7)

which after application of the Euler–Lagrange field equation

$\frac{\partial L}{\partial {\zeta }_a\left(x\right)}-{\partial }_{\mu }\frac{\partial L}{\partial {\partial }_{\mu }{\zeta }_a\left(x\right)}=0$(2.8)

is found to be conserved:

${\partial }_{\mu }{J}_i^{\mu }\left(x\right)=0.$(2.9)

The associated time-independent charge is

$G_i=\int d^{3}x{J}_i^0\left(x\right).$(2.10)

Provided that the vacuum state of the theory is left invariant by all of the symmetry transformations so that

$U\left(\right\{{\omega }_i\left\}\right)|0⟩=|0⟩,$(2.11)

or equivalently

$G_i|0⟩=0,$(2.12)

there are mass degenerate multiplets of states in the physical spectrum. When both the Lagrangian and the vacuum state are invariant under the global symmetry transformation, the symmetry is said to be realized à la Wigner–Weyl [Reference Wigner13, Reference Weyl14].

To establish that in the case of a Wigner–Weyl realized global symmetry there are mass degenerate multiplets of states in the theory, we need to recall some properties of single-particle states. For each of the quantum fields ${\zeta }_a\left(x\right)$ , one can effectively associate a single-particle state $|p;\alpha ⟩$ , with $p^{\mu }=(\sqrt{{\vec{p}}^2+m_{\alpha }^2},\vec{p})$ , by the Lehmann, Symanzik, Zimmermann (LSZ) prescription [Reference Lehmann, Symanzik and Zimmermann15]. For a scalar field ${\zeta }_a$ , for example, one writes

(2.13)

where $|0⟩$ is the vacuum state and $⟨0\left|{\chi }_a\right(0\left)\right|p;\alpha ⟩=\sqrt{Z}.$ (Since for single-particle states, there is no distinction between in and out states, one can take the limit either as $x^0$ goes to $+\infty$ or $-\infty$ .) The notation $px$ here is a shorthand for $p^{\mu }{x}_{\mu }$ , while $A{\overleftrightarrow{\partial }}_{0}B\equiv A{\partial }_{0}B-\left({\partial }_{0}A\right)B$ . Acting with $U^{-1}\left(\right\{{\omega }_i\left\}\right)$ on the preceding expression gives

$U^{-1}\left(\right\{{\omega }_i\left\}\right)|p;a⟩=\underset{x^0\to \pm \infty }{lim}\frac{-i}{\sqrt{Z}}\int d^{3}x{e}^{ipx}{\overleftrightarrow{\partial }}_0{U}^{-1}(\left\{{\omega }_i\right\}\left){\chi }_a\right(x\left)\right|0⟩.$(2.14)

If one assumes that the vacuum state is invariant under the symmetry transformation, so that

$U\left(\right\{{\omega }_i\left\}\right)|0⟩=|0⟩,$(2.15)

then the unitary operator $U\left(\right\{{\omega }_i\left\}\right)$ can be inserted with impunity between the vacuum state and ${\chi }_a\left(x\right)$ . In this case, one can use Eq. (2.2) to immediately deduce that the single-particle states $|p;a⟩$ transform as

$U^{-1}\left(\right\{{\omega }_i\left\}\right)|p;a⟩=R_{ab}(\left\{{\omega }_i\right\}\left)\right|p;\beta ⟩.$(2.16)

That is, these states transform irreducibly among themselves when acted upon by the unitary operator $U^{-1}$ .

The Hamiltonian of the theory, $H$ , because of the invariance of $L$ under the symmetry transformations, commutes with $U^{-1}\left(\right\{{\omega }_i\left\}\right)$ :

$[H,U^{-1}(\left\{{\omega }_i\right\}\left)\right]=0.$(2.17)

By definition, the action of $H$ on a single-particle state at rest gives the mass of that state

$H|p;a{⟩}_{rest}=m_a|p;a{⟩}_{rest}.$(2.18)

Using the preceding equations, it follows that

$0=\left(H,U^{-1}\left(\right\{{\omega }_i\left\}\right)\right)|p;a{⟩}_{rest}=R_{ab}(\left\{{\omega }_i\right\}\left)\right(m_a-m_b\left)\right|p;b{⟩}_{rest}.$(2.19)

Because the preceding must hold for all transformations $R_{ab}\left(\right\{{\omega }_i\left\}\right)$ , it follows that

$m_a=m_b.$(2.20)

Thus, provided that the vacuum state is invariant under the symmetry, then each irreducible representation corresponds to a multiplet of single-particle states degenerate in mass.

3 Local $U\left(1\right)$ Invariance and QED

An explicit example of a continuous global invariance is afforded by the free field Dirac action

$S_{Dirac}[\psi ,\bar{\psi }]=\int d^{4}x{L}_{Dirac}\left(x\right),$(3.1)

with associated Lagrangian

$L_{Dirac}\left(x\right)=-\bar{\psi }\left(x\right)\left({\gamma }^{\mu }\frac{1}{i}{\partial }_{\mu }+m\right)\psi \left(x\right),$(3.2)

whose Euler–Lagrange equations are simply the free Dirac equation

$\left({\gamma }^{\mu }\frac{1}{i}{\partial }_{\mu }+m\right)\psi \left(x\right)=0$(3.3)

and its Hermitian conjugate. Said Lagrangian is invariant under the global, continuous phase transformation

$\psi \left(x\right)\to e^{i{q}_{\psi }\omega }\psi \left(x\right);\bar{\psi }\left(x\right)\to e^{-i{q}_{\psi }\omega }\bar{\psi }\left(x\right),$(3.4)

which corresponds to a $U\left(1\right)$ Abelian group. (In this case, the structure constants vanish: $c_{ijk}=0$ .) Here $\omega$ is a real space-time–independent parameter and $q_{\psi }$ is a real number that for electrons is chosen by convention (which can be traced to Benjamin Franklin) as $q_e=-1$ . For infinitesimal parameter $\delta \omega$ , $\psi \left(x\right)\to \psi \left(x\right)+\delta \psi \left(x\right)$ with $\delta \psi \left(x\right)=i{q}_{\psi }\delta \omega \psi \left(x\right)$ . Similarly $\delta \bar{\psi }\left(x\right)=-i{q}_{\psi }\delta \omega \bar{\psi }\left(x\right)$ . This invariance and the application of the field equations leads via Noether’s theorem to the conserved electromagnetic current operator

$J_{EM}^{\mu }\left(x\right)=q_{\psi }\bar{\psi }\left(x\right){\gamma }^{\mu }\psi \left(x\right)=-\bar{\psi }\left(x\right){\gamma }^{\mu }\psi \left(x\right),$(3.5)

with ${\partial }_{\mu }{J}_{EM}^{\mu }\left(x\right)=0$ and the time-independent electric charge operator

$Q_{EM}=\int d^{3}r{J}_{EM}^0\left(x\right).$(3.6)

Since the vacuum carries zero electric charge so that $Q_{EM}|0⟩=0$ , it follows that this symmetry is realized à la Wigner–Weyl and results in a mass degeneracy. In this case, the degeneracy is between the electron and positron masses.

Now suppose one allows the transformation parameter to vary from point to point in space-time so that $\omega =\omega \left(x\right)$ . Under this local or gauged $U\left(1\right)$ phase transformation,

$\psi \left(x\right)\to e^{i{q}_{\psi }\omega \left(x\right)}\psi \left(x\right);\bar{\psi }\left(x\right)\to e^{-i{q}_e\omega \left(x\right)}\bar{\psi }\left(x\right),$(3.7)

the free Dirac Lagrangian is no longer invariant:

$L\to L-J_{EM}^{\mu }{\partial }_{\mu }\omega .$(3.8)

In order to restore the invariance, one simply replaces the derivative by a covariant derivative

${\partial }_{\mu }\to D_{\mu }={\partial }_{\mu }-ie{A}_{\mu }\left(x\right),$(3.9)

where the four-vector potential $A_{\mu }\left(x\right)$ transforms as

$e{A}_{\mu }\left(x\right)\to e{A}_{\mu }\left(x\right)+{\partial }_{\mu }\omega \left(x\right).$(3.10)

Here we have introduced the QED coupling $e$ . Demanding local or gauge invariance then results in the action of Quantum Electrodynamics (QED). (For selected fundamental papers in the development of QED, see, for example, reference [Reference Schwinger16].)

$S_{QED}[\psi ,\bar{\psi },A^{\mu }]=\int d^{4}x{L}_{QED}\left(x\right),$(3.11)

where

$L_{QED}\left(x\right)=L_{Dirac}\left(x\right)+e{J}_{EM}^{\mu }\left(x\right)A_{\mu }\left(x\right)+L_{Maxwell}\left(x\right).$(3.12)

Here the Maxwell Lagrangian

$L_{Maxwell}\left(x\right)=-\frac{1}{4}{F}^{\mu \nu }\left(x\right)F_{\mu \nu }\left(x\right),$(3.13)

with gauge-invariant field strength

$F_{\mu \nu }\left(x\right)={\partial }_{\mu }{A}_{\nu }\left(x\right)-{\partial }_{\nu }{A}_{\mu }\left(x\right),$(3.14)

provides the kinetic term for the photon field. Thus we extract the main lesson that the interaction term between the electron field and the photon field arises as a consequence of the imposition of the local or gauge invariance. For QED, the interaction is the coupling of the conserved electromagnetic vector current to the vector photon field: $e{J}_{EM}^{\mu }\left(x\right)A_{\mu }\left(x\right)$ . Any field carrying an electric charge contributes to the current and directly couples to the photon. Note that since photons themselves carry zero electric charge, they do not have any direct self-interactions. By the late 1940s, R. P. Feynman, J. Schwinger, S. I. Tomonaga and F. Dyson established [Reference Schwinger16] that QED could be consistently interpreted order by order in perturbation theory once the coupling and mass of the electron were fixed as inputs.

Theoretical calculations in QED can be performed perturbatively in powers of the fine structure constant $\alpha =\frac{e^2}{4\pi }$ , whose numerical value at the electron mass scale is experimentally extracted as [Reference Morel, Yao, Cladé and Guellati-Khélifa17] ${\alpha }^{-1}=137.035999206\left(81\right)$ . At present, these calculations have been carried out with exquisite precision and exhibit remarkable agreement with electrodynamic measurements, which have been performed with incredible accuracy. For example, consider the single-electron matrix element of the electromagnetic current

$⟨e^{-}\left(p_1\right)\left|J_{EM}^{\mu }\right(0\left)\right|e^{-}\left(p_2\right)⟩={\bar{U}}_e\left(p_1\right)\left({\gamma }^{\mu }{F}_1\left(q^2\right)+{\sigma }^{\mu \nu }{q}_{\nu }{F}_2\left(q^2\right)\right)U_e\left(p_2\right),$(3.15)

which encodes the electron electromagnetic properties. This decomposition is a general consequence of Lorentz invariance and the fact that the electromagnetic current $J_{EM}^{\mu }$ is conserved. Here $\left|e^{-}\right(p_1)⟩$ and $\left|e^{-}\right(p_2)⟩$ are single-electron states with energy-momentum $p_1^{\mu }=\left(\sqrt{{\vec{p}}_1^2+m^2},{\vec{p}}_1\right)$ and $p_2^{\mu }=\left(\sqrt{{\vec{p}}_2^2+m^2},{\vec{p}}_2\right)$ respectively and $q^{\mu }=p_2^{\mu }-p_1^{\mu }$ is the momentum transfer. Note that the form of this decomposition holds if the electron is replaced by any single fermion state. Moreover, it is applicable in any theory where there is a conserved electromagnetic current. This is true if the electromagnetic current is associated with a gauged symmetry as in QED or is an external current as, for example, in the theory of strong interactions, QCD. All that will change are the form factors $F_1\left(q^2\right)$ and $F_2\left(q^2\right)$ . In some cases, such as QED, these form factors can be computed perturbatively. In other cases, like the theory of strong interactions, the computation of the form factors, in general, requires a nonperturbative analysis.

The physical interpretation of the form factors at zero momentum transfer is secured by further coupling the electron to an external static electromagnetic field. From the coupling to the external electric field, one deduces that $F_1\left(0\right)$ is the charge on the electron. Since $Q_{EM}$ generates the electric charge symmetry, it follows that

$[Q_{EM},\bar{\psi }(x\left)\right]=\bar{\psi }\left(x\right),$(3.16)

which acting on the vacuum gives

$Q_{EM}\bar{\psi }\left(x\right)|0⟩-\bar{\psi }\left(x\right)Q_{EM}|0⟩=\bar{\psi }\left(x\right)|0⟩.$(3.17)

Using $Q_{EM}|0⟩=0$ , it follows that

$Q_{EM}\left|e^{-}\right(p_1)⟩=|e^{-}\left(p_1\right)⟩.$(3.18)

Taking the matrix element with $⟨e^{-}\left(p_1\right)|$ and using the preceding decomposition, Eq. (3.15), in conjunction with the fact that the electromagnetic current is conserved so the time-independent electric charge operator is $Q_{EM}=\int d^{3}r{J}_{EM}^0\left(x\right)$ , then yields

$F_1\left(0\right)=q_e=-1,$(3.19)

which is the experimentally observed value. Note that if the electron states are replaced by muon states, one again finds $F_1\left(0\right)=-1$ , while if electron states are replaced by proton states, $F_1\left(0\right)=1$ , which gives the electric charge of the proton. Note that the value of $F_1\left(0\right)$ for the electron is unchanged by the higher-order perturbative QED interactions or in the proton case by electromagnetic or strong interactions. That is, the charge form factor at zero momentum transfer does not get renormalized. This is a consequence of electromagnetic current conservation. Moreover, the fact that $F_1\left(0\right)$ has the same magnitude for electrons, muons and protons reflects a universality of the QED interaction.

On the other hand, the coupling to an external magnetic field dictates that the magnetic moment operator for the electron is

${\vec{\mu }}_e=-{\mu }_B{g}_e\frac{1}{2}\vec{\sigma },$(3.20)

where the $\vec{\sigma }$ are the three $2\times 2$ Pauli matrices. Here

${\mu }_B=\frac{e}{2m}$(3.21)

is the Bohr magneton and the electron $g_e$ factor is

$g_e=2(1+F_2\left(0\right))$(3.22)

so that

$F_2\left(0\right)=\frac{1}{2}(g_e-2)\equiv a_e.$(3.23)

Free Dirac theory (coupled to the external EM field) gives $F_2\left(0\right){|}_{Dirac}=a_e{|}_{Dirac}=0$ , thus accounting for the dominant contribution $g_e{|}_{Dirac}=2$ , which was one of its major successes. However, radiative (loop) corrections due to QED modify this result, producing a nontrivial anomalous magnetic moment $a_e$ . The 1-loop $O\left(\alpha \right)$ theoretical calculation giving $a_e^{1loop}=\frac{\alpha }{2\pi }$ was first performed by J. Schwinger [Reference Schwinger18] in 1948. Subsequently the calculation has been extended to include terms analytically [Reference Laporta and Remiddi19] of $O\left({\alpha }^3\right)$ and numerically through $O\left({\alpha }^5\right)$ yielding [Reference Aoyama, Kinoshita and Nio20]

$a_e^{th}=0.00115965218161\left(23\right).$(3.24)

(Note that this value includes the contributions from the weak and strong interactions in addition to the pure QED result.) Experimentally, the anomalous magnetic moment of the electron has been measured [Reference Hanneke, Fogwell Hoogerheide and Gabrielse21] as

$a_e^{exp}=0.00115965218073\left(28\right),$(3.25)

so there is agreement to 10 significant figures. Both the experimental measurement and theoretical calculation of this anomalous magnetic moment of the electron are truly monumental achievements. Their agreement certainly provides credence to the validity of QED.

4 Global Symmetry Structure of the Strong Interactions

While no viable theory of the strong nuclear force holding the nucleus together yet existed, nonetheless, shortly after the 1932 J. Chadwick discovery [Reference Chadwick22] of the neutron with a mass nearly degenerate with that of the proton, W. Heisenberg [Reference Heisenberg23] proposed that this near-mass degeneracy could be accounted for if the interactions exhibit an $SU(2{)}_V$ global vector symmetry realized à la Wigner–Weyl with the proton and neutron transforming as a doublet. The charge operators, $T_{i}i=1,2,3$ , of this non-Abelian strong isotopic symmetry satisfy the $SU\left(2\right)$ Lie algebra

$[T_i,T_j]=i{ϵ}_{ijk}{T}_k,$(4.1)

where ${ϵ}_{ijk}$ is the Levi–Civita tensor satisfying ${ϵ}_{123}=1$ . The associated conserved vector currents are $SU(2{)}_V$ generalizations of the conserved electromagnetic current except now the currents carry a net electric charge. The small explicit breaking of the isospin symmetry producing the relatively small neutron-proton mass difference is today recognized as resulting from a combination of the up-down quark mass differences and the perturbative electromagnetic interactions, which affects differently the charged and neutral components of the multiplet. The origin of each of these effects lies outside the strong interaction. Thus the strong interaction itself respects the global $SU(2{)}_V$ isospin symmetry. After the introduction of a new conserved quantum number dubbed strangeness following the discovery of the neutral and charged spin zero kaons and the baryonic $\Lambda$ , this global classification symmetry was extended to an $SU(3{)}_V$ symmetry independently by M. Gell-Mann [Reference Gell-Mann24] and Y. Ne’eman [Reference Ne’eman25] in 1961. (There is far larger mass splitting among the components of mesonic and baryonic $SU(3{)}_V$ multiplets relative to that within the $SU(2{)}_V$ multiplets. Today, this is recognized as due to the $s$ quark mass being larger than the $u$ and $d$ masses.)

The charged and neutral pions are the lowest-mass hadronic states. They transform as a triplet under the global $SU(2{)}_V$ isospin symmetry, which explains the near-degeneracy of the ${\pi }^{\pm }$ and ${\pi }^0$ masses. It was established that many of the pion properties could be accounted for by assuming there existed partially conserved axial vector currents (PCAC) [Reference Gell-Mann26] with the small explicit symmetry breaking being proportional to the square of the pion mass. The origin of this small explicit breaking mass is due to the up and down quark masses and thus again lies outside the strong interaction. Consequently, the strong interactions have a conserved global $SU(2{)}_A$ axial symmetry and associated conserved axial vector currents. However, since no near-mass-degenerate opposite parity states exist, it follows that this symmetry is not realized à la Wigner–Weyl. The understanding of the way this symmetry is realized proved pivotal to the understanding of the weak interaction and hence the construction of the Standard Model.

5 Fermi Theory of the Weak Interactions

Attempting to model the short-ranged ( $\sim {10}^{-18}$ m) weak nuclear force responsible for nuclear beta decay data, E. Fermi [Reference Fermi27–Reference Fermi29] introduced in 1933 a local current-current coupling. The currents were taken as vector currents in analogy with the current appearing in electrodynamics, but they were electric-charge-carrying currents. The Fermi model conserved parity. However in 1956, C. N. Yang and T. D. Lee raised [Reference Yang and Lee30] the possibility that parity might be violated by the weak interactions. The experiment they proposed to test this hypothesis was successfully performed by C.-S. Wu and her collaborators [Reference Wu, Ambler, Hayward, Hoppes and Hudson31] in 1957 with the conclusion that parity was indeed violated by the weak interactions. To account for this parity violation, R. Feynman and M. Gell-Mann [Reference Feynman and Gell-Mann32] and independently R. Marshak and E. C. G. Sudarshan [Reference Marshak and Sudarshan33] modified the Fermi model so that charged currents were of a vector-axial vector (V-A) form

$J_{cc}^{\mu }=V_{cc}^{\mu }-A_{cc}^{\mu }$(5.1)

and the modified Fermi theory interaction Lagrangian reads

$L_{Fermi}=G_F{J}_{cc}^{\mu }{J}_{cc\mu }.$(5.2)

Here $G_F\sim {10}^{-5}$ GeV ${}^{-2}$ is the Fermi constant, which sets the scale of the weak interactions, and the currents were composed of a sum of hadronic and leptonic pieces. Moreover, they and independently S. Gershtein and Ya. B. Zeldovich [Reference Gershtein and Zeldovich34] proposed that the hadronic piece of the vector current is the conserved vector current of the global isotopic spin $SU(2{)}_V$ symmetry of strong interactions introduced by Heisenberg. This is referred to as the conserved vector current (CVC) hypotheis. A bit later, M. Gell-Mann further proposed [Reference Gell-Mann26] that the hadronic piece of the axial vector current is the conserved axial vector current of the global $SU(2{)}_A$ symmetry of the strong interaction. The current-current interaction could account reasonably well at the time for the nuclear beta decay data using lowest-order perturbation theory since the amplitudes varied as $G_F{E}^2$ and the energies were less than 1 GeV. However, the model was internally inconsistent once higher-order (loop) corrections were included.

As early as 1948, attempting to more closely mimic the successful QED interaction, O. Klein [Reference Klein35] suggested replacing the local current-current Fermi model with a model that coupled the charged weak interaction currents to charged intermediate vector boson fields, $W_{\mu }^{\pm }$ , as

$L_{cc}=g_W(J_{cc}^{\mu }{W}_{\mu }^{+}+J_{cc}^{†\mu }{W}_{\mu }^{-}).$(5.3)

The vector particle excitations, $W^{\pm }$ , of the vector fields need to be far more massive than the momentum exchanged to account for the short-range nature of the weak interaction processes probed at that time. To reproduce the results of the Fermi theory, one simply approximates the massive vector (Proca) propagator by its ultralocal form ( $M_W^2\gg q^2$ ),

${\Delta }_{\mu \nu }\left(q\right)=\frac{{\eta }_{\mu \nu }+\frac{q_{\mu }{q}_{\nu }}{M_w^2}}{q^2+M_W^2-iϵ}\to \frac{{\eta }_{\mu \nu }}{M_W^2},$(5.4)

while identifying $G_F\sim \frac{g_W^2}{M_W^2}$ . Here, ${\eta }_{\mu \nu }$ is the Minkowski space metric tensor. Taking $g_W\sim {10}^{-1}$ , which is the strength of the electromagnetic coupling, gives $M_W\sim 100\text{GeV}$ . Unfortunately, simply mimicking the form of the QED interaction is not enough to cure the model of its sicknesses. The root of the problem lies in the origin of the vector mass. Simply adding a direct $W^{\pm }$ mass term to the model Lagrangian yields a Proca vector propagator, which does not fall off at large energies as does the massless photon propagator in QED. Thus, as in the local current-current Fermi theory, unitarity is violated at energies of the order of 300 GeV.

6 Nambu–Goldstone Realization of $SU(2{)}_A$

A significant advance in the understanding of the realization of the global $SU(2{)}_A$ symmetry of the strong interactions was achieved by Y. Nambu [Reference Nambu38] who was inspired by the J. Bardeen, L. Cooper, R. Schrieffer (BCS) theory [Reference Bardeen, Cooper and Schrieffer36],[Reference Bardeen, Cooper and Schrieffer37] of superconductivity, which accounts for the attractive force leading to bound Cooper pairs of electrons in a spin singlet state as arising from their interaction with phonons in the lattice. Due to the condensate of Cooper pairs, the BCS ground state does not exhibit the full symmetry structure of the BCS Hamiltonian. In 1960, Nambu suggested that the vacuum state of the strong interactions, in analogy to the superconducting ground state, might not respect the full symmetries of the theory, and the elementary particles might acquire mass in a manner analogous to the energy gap of the quasiparticle excitations of BCS theory. To study this conjecture, Nambu and G. Jona-Lasinio [Reference Nambu and Jona-Lasinio39] introduced a Lorentz invariant model, the NJL model, in which the Lagrangian is invariant under independent vector and axial vector global $U\left(1\right)$ phase transformations. This is tantamount to having independent phase transformations for the left-handed and right-handed components of the fermion field:

$\begin{array}{cc}{f}_L\left(x\right)& =\frac{1}{2}(1-{\gamma }_5)f\left(x\right),\\ f_R\left(x\right)& =\frac{1}{2}(1+{\gamma }_5)f\left(x\right).\end{array}$(6.1)

Invariance under the axial transformation forbids a direct fermion mass term. This NJL model, whose interaction term was a chirally invariant four-fermion coupling, was self-consistently analyzed in mean field approximation. A nontrivial vacuum fermion-antifermion condensate emerged, which broke the axial symmetry and resulted in a nonzero fermion mass. Thus while the model Lagrangian is invariant under the axial symmetry, the vacuum state is not. The symmetry is said to be spontaneously broken. (The nomenclature was introduced by S. Glashow and M. Baker [Reference Glashow and Baker41]. Unfortunately it is not an accurate description of what is going on, as the symmetry is not really broken. A better name is hidden or secret symmetry as coined by S. Coleman [Reference Coleman42]. Nonetheless, the spontaneous symmetry breaking moniker stuck.) In addition, the model predicted the appearance of a massless composite pseudoscalar particle whose interactions were derivatively coupled.

A very useful phenomenological description of superconductivity predating BCS is the Ginzburg–Landau Model [Reference Ginzburg and Landau43]. The model introduces an electrically charged scalar order parameter field $\varphi \left(\vec{r}\right)$ representing the wavefunction of the condensate of Cooper pairs whose Hamiltonian,

$H_{GL}={\varphi }^{*}\left(\vec{r}\right)\frac{1}{2m}\left(\frac{1}{i}\nabla -2e\vec{A}\left(\vec{r}\right)\right)+V\left({\varphi }^{*}\varphi \right),$(6.2)

with potential

$V\left({\varphi }^{*}\varphi \right)=\beta {\varphi }^{*}\varphi +\frac{1}{2}\gamma ({\varphi }^{*}\varphi {)}^2$(6.3)

respects a U(1) gauge invariance. The coefficients, $\beta$ and $\gamma$ , are temperature dependent with $\beta$ changing sign at the critical temperature, $T_c$ , going negative for $T<T_c$ . Thus for these temperatures the potential minimum is at ${\varphi }^{*}\varphi =-\frac{\beta }{\gamma }$ . The magnitude of the order parameter is fixed, but the phase is arbitrary corresponding to a family of degenerate ground states. The selection of a particular ground state corresponds to a spontaneous breaking of the $U\left(1\right)$ symmetry of the Hamiltonian by the ground state. Thus this nonrelativistic model exhibits a spontaneous symmetry breaking and is a precursor to the Lorentz–invariant U(1) Goldstone and Higgs models we shall soon address.

An earlier example of a spontaneously broken global symmetry is afforded by the W. Heisenberg description [Reference Heisenberg44] of ferromagnetism using a Hamiltonian,

$\begin{array}{c}{H}_{\text{Heisenberg}}=-\frac{1}{2}\sum _{x,y}{J}_{x-y}{\vec{S}}_x\cdot {\vec{S}}_y,\end{array}$(6.4)

where ${\vec{S}}_x$ denotes the spin at site $x$ and $J$ is the strength of the interaction, which depends on the distance between the sites $x$ and $y$ and is assumed to fall rapidly as the distance becomes large. The model is invariant under a simultaneous rotation of all the spins. For positive $J$ , the lowest energy state is one with all spins aligned; the particular direction is arbitrary. Thus there is a degeneracy of ground states. From one such ground state, one can make a rotation of all the spins and get another ground state degenerate in energy. Once a particular ground state is chosen, the rotational symmetry of the Hamiltonian is spontaneously broken. The model exhibits an excitation, the spin wave, whose energy vanishes in long wavelength limit.

While the Nambu–Jona–Lasinio model yielded a nonzero fermion mass, it did not prove to be the correct theory of strong interactions. In fact, the model was actually inconsistent when higher-order radiative corrections were taken into account. (It is nonrenormalizable.) An alternative model exhibiting a global $SU(2{)}_V\times SU(2{)}_A$ symmetry where the axial symmetry is spontaneously broken, resulting in a nonzero fermion mass was suggested by J. Schwinger [Reference Schwinger40]. He studied aspects of what later would be called the Gell-Mann–Levy $\sigma$ model [Reference Gell-Mann and Levy45]. The model degrees of freedom consisted of an $SU(2{)}_V$ nucleon doublet $N$ (proton and neutron), the three pions, $\vec{\pi }$ , forming an $SU(2{)}_V$ triplet and a hypothetical $SU(2{)}_V$ singlet field $\sigma$ . The $SU(2{)}_V\times SU(2{)}_A$ symmetry is realized as

$\begin{array}{cc}N\left(x\right)& \to \left(1+i\delta {\vec{\omega }}_V\frac{\vec{\sigma }}{2}+i\delta {\vec{\omega }}_A\cdot \frac{\vec{\sigma }}{2}{\gamma }_5\right)N\left(x\right),\\ \sigma \left(x\right)& \to \sigma \left(x\right)+\delta {\vec{\omega }}_A\cdot \vec{\pi }\left(x\right),\\ \vec{\pi }\left(x\right)& \to \vec{\pi }\left(x\right)-\delta {\vec{\omega }}_V\times \vec{\pi }\left(x\right)-\delta {\vec{\omega }}_A\sigma \left(x\right),\end{array}$(6.5)

and forbids a fermion mass term. Here the $\vec{\sigma }$ are the three $2\times 2$ Pauli matrices. The chirally invariant interaction is of the Yukawa form:

$L_{\text{Yukawa}}=g_{\text{Yukawa}}\bar{N}(\sigma +i\vec{\sigma }\cdot \vec{\pi }{\gamma }_5)N.$(6.6)

If the $\sigma$ field develops a nontrivial vacuum expectation value, $⟨\sigma ⟩\ne 0$ , the fermion mass $m_N=g_{\text{Yukawa}}⟨\sigma ⟩$ is generated. This Schwinger mechanism of fermion mass generation is basically how fermion masses are produced in the standard electroweak theory.

At roughly the same time as Nambu’s work, J. Goldstone [Reference Goldstone46] studied the simplest Lorentz-invariant model exhibiting a spontaneous global continuous symmetry breaking. It consisted of a single complex scalar field $\varphi \left(x\right)$ whose dynamics is invariant under a global $U\left(1\right)$ phase transformation $\varphi \left(x\right)\to e^{i\omega }\varphi \left(x\right)$ . The invariant Lagrangian is

$\begin{array}{c}{L}_{\text{Goldstone}}=-{\partial }_{\mu }{\varphi }^{†}\left(x\right){\partial }^{\mu }\varphi \left(x\right)-V\left(\varphi \right)\end{array}$(6.7)

with

$V\left(\varphi \right)={\mu }^2{\varphi }^{†}\left(x\right)\varphi \left(x\right)+\frac{1}{2}\lambda ({\varphi }^{†}\left(x\right)\varphi \left(x\right){)}^2.$(6.8)

So long as ${\mu }^2>0$ , the potential is minimized at $\varphi =0$ and the spectrum consists of a charged scalar and its antiparticle degenerate in mass, namely a Wigner–Weyl realization. But for ${\mu }^2<0$ , the potential takes the form of a sombrero as displayed in Figure 6.1. In this case, the potential is minimized for ${\varphi }^{†}\varphi =\frac{v^2}{2}$ , where $v^2=-\frac{{\mu }^2}{\lambda }$ . Hence the lowest energy states are such that $\varphi$ has magnitude $\frac{v}{\sqrt{2}}$ but arbitrary phase and the vacuum state is infinitely degenerate. Once the phase is fixed (the particular value is physically unobservable), the global symmetry is spontaneously broken. Choosing the phase to vanish so $⟨\varphi ⟩=v$ is real and expanding about that point as

Figure 6.1 Sombrero potential: massless mode rolls along bottom of well; massive mode sloshes up and down wall. The colorbar represents the value of the potential value ranging from its minimum (dark blue) to its maximum (yellow).

$\varphi \left(x\right)=\frac{1}{\sqrt{2}}(v+{\varphi }_1(x)+i{\varphi }_2(x\left)\right)$(6.9)

with ${\varphi }_1,{\varphi }_2$ Hermitian fields, the model describes two spin zero particles, one with mass $m_{{\varphi }_1}=\sqrt{\lambda }v$ , while the other is massless, $m_{{\varphi }_2}=0$ . Once again, there is a massless spin zero particle associated with a spontaneously broken continuous global symmetry. The massless particle is referred to as a Nambu–Goldstone boson (NGB) and the spontaneously broken symmetry constitutes a Nambu–Goldstone realization of the continuous global symmetry. In Nambu–Goldstone realizations, the action is still invariant under the symmetry transformations, which continue to be represented by unitary operators so that

$U^{-1}\left(\right\{{\omega }_i\left\}\right)L\left(x\right)U\left(\right\{{\omega }_i\left\}\right)=L\left(x\right).$(6.10)

Now, however, the vacuum state does not respect the symmetry, so

$U\left(\right\{{\omega }_i\left\}\right)|0⟩\ne |0⟩.$(6.11)

J. Goldstone, A. Salam and S. Weinberg [Reference Goldstone, Salam and Weinberg47] provided a general proof of a theorem which dictates the appearance of a massless, spin zero, Nambu–Goldstone boson (NGB) for every spontaneously broken continuous global internal symmetry in any model with manifest Lorentz invariance. The proof is independent of the particular dynamics employed to spontaneously break the symmetry. This constituted an apparent death knoll for all such models, as no such massless spin 0 particles were observed.

7 Yang–Mills Theory

C. N. Yang and R. Mills [Reference Yang and Mills48] were the firstFootnote ¹ to construct a mathematically consistent four space-time dimensional theory containing spin-one particles which carry nontrivial gauge group quantum numbers. To do so requires a non-Abelian gauge theory that generalizes the Abelian U(1) gauge theory of QED to non-Abelian gauge groups. (In their original paper, they focused on an $SU\left(2\right)$ group. The more general case soon followed.) This involves promoting the local phase invariance of the Abelian model to a matrix-valued local phase invariance. Consider a non-Abelian gauge group with Lie algebra of dimension $n$ , which is also the number of group generators $G_i$ , group parameters ${\omega }_i\left(x\right)$ and vector gauge fields $A_i^{\mu }$ where $i=1,2,\dots ,n$ . It proves convenient to define the matrix-valued field $A^{\mu }=A_i^{\mu }{\tau }_i$ , where ${\tau }_i$ are matrix representations of the group generators $G_i$ that satisfy the non-Abelian algebra

$[G_i,G_j]=i{c}_{ijk}{G}_k$(7.1)

with group structure constants $c_{ijk}$ . It follows that the $A^{\mu }$ transformation takes the form

$A_{\mu }\left(x\right)\to R\left(\omega \right(x\left)\right)A_{\mu }\left(x\right)R^{-1}\left(\omega \right(x\left)\right)-\frac{i}{g}R\left(\omega \right(x\left)\right){\partial }_{\mu }{R}^{-1}\left(\omega \right(x\left)\right),$(7.2)

where $R\left(\omega \right(x\left)\right)=e^{i{\omega }_i\left(x\right){\tau }_i}$ is a matrix representation of the non-Abelian group element.

Yang and Mills constructed the invariant Lagrangian

$L_{YM}\left(x\right)=-\frac{1}{4}{F}_{\mu \nu i}\left(x\right)F_i^{\mu \nu }\left(x\right),$(7.3)

where

$F_i^{\mu \nu }\left(x\right)={\partial }^{\mu }{A}_i^{\nu }\left(x\right)-{\partial }^{\nu }{A}_i^{\mu }\left(x\right)+g{c}_{ijk}{A}_j^{\mu }\left(x\right)A_k^{\nu }\left(x\right)$(7.4)

is the Yang–Mills field strength, which transforms as the adjoint representation. Contrary to the QED photon field, the non-Abelian vectors are self-coupled and the Yang–Mills Lagrangian contains three- and four-point vector interactions whose couplings are related in a definite way.

Note, however, that the mass term $A_i^{\mu }\left(x\right)A_{\mu i}\left(x\right)$ is not invariant under the above gauge transformation and thus is forbidden. Consequently, it would appear that to maintain the non-Abelian gauge symmetry, the non-Abelian vectors are necessarily massless. Thus the theory was initially considered a failure since it seemed incapable of explaining the short-ranged weak interactions nor did it seem relevant for the strong interactions. As it turned out, Yang–Mills theories provide the proper framework to describe both the strong and electroweak interactions.

8 Quantum Chromodynamics

Quantum Chromodynamics (QCD) as the theory of strong interactions was introduced in the early 1970s by M. Gell-Mann, H. Fritzsch, W. Bardeen, and H. Leutwyler [Reference Gell-Mann49], [Reference Fritzsch, Gell-Mann, Jackson and Roberts50–Reference Fritzsch, Gell-Mann and Leutwyler52]. It is an unbroken $SU(3{)}_c$ gauge theory where the local symmetry involves transformations in the space of a new quantum number dubbed color. The Yang–Mills fields mediating the interaction are the massless self-interacting vector gluon fields, $A_i^{\mu }\left(x\right),i=1,2,\dots 8$ , which transform as in Eq. (7.2) and also interact with the fermionic spin 1/2 quark fields which transform as the fundamental (triplet) representation. The QCD Lagrangian is

$L_{QCD}=\sum _{\alpha }L(q_a^{\alpha },D_{\mu }{q}_a^{\alpha })-\frac{1}{4}{G}_i^{\mu \nu }{G}_{\mu \nu i},$(8.1)

where

$L(q_a^{\alpha },D_{\mu }{q}_a^{\alpha })=-{\bar{q}}_a^{\alpha }{\gamma }^{\mu }\frac{1}{i}{D}_{\mu }{q}_a^{\alpha }-m_{\alpha }{\bar{q}}_a^{\alpha }{q}_a^{\alpha },$(8.2)

with covariant derivative

$D_{\mu }{q}_a^{\alpha }=\left({\delta }_{ab}{\partial }_{\mu }-i{g}_3{\left(\frac{{\lambda }_i}{2}\right)}_{ab}{A}_{\mu i}\right)q_b^{\alpha }.$(8.3)

The gluon field strength,

$G_i^{\mu \nu }={\partial }^{\mu }{A}_i^{\nu }-{\partial }^{\nu }{A}_i^{\mu }+g_3{f}_{ijk}{A}_j^{\mu }{A}_k^{\nu },$(8.4)

transforms as the adjoint (octet) representation under $SU(3{)}_c$ . In the preceding equations, $\alpha =\{u,d,c,s,t,b\}$ is a quark flavor label, while $a=1,2,3$ , and $i=1,2,..,8$ , are color labels. The ${\lambda }_i$ are the Gell-Mann matrices, which form the $3\times 3$ fundamental representation for $SU(3{)}_c$ , while the $f_{ijk}$ are the $SU(3{)}_c$ group structure constants and $g_3$ is the $SU(3{)}_c$ gauge coupling.

While the role of a color quantum as a necessary property for the spin 1/2 quarks was emphasized very early [Reference Greenberg53–Reference Han and Nambu56] in order for the quark model for baryons to be consistent with the spin-statistics theorem, the dynamical importance of having a non-Abelian local symmetry describing the interactions of quarks did not really become manifest until the discovery of asymptotic freedom by D. Gross and F. Wilczek [Reference Gross and Wilczek57] and independently by H. D. Politzer [Reference Politzer58] in 1973 who demonstrated that due to the non-Abelian QCD vector gluon self-couplings, the interaction strength (logarithmically) decreases at shorter and shorter distances or equivalently at higher and higher energies. Note that this running of the QCD coupling is opposite to the case of the Abelian QED where the interaction strength decreases at longer distances due to electric charge screening.

Explicitly, D. Gross, F. Wilczek and H. D. Politzer computed the 1-loop running of the gauge coupling in a Yang–Mills theory with gauge group $G$ and $n_R$ fermions carrying gauge representation $R$ and showed that asymptotic freedom emerges provided

$\sum _R{n}_{R}T\left(R\right)<\frac{11}{4}{C}_2\left(G\right).$(8.5)

Here $C_2\left(G\right)$ is the value of the quadratic Casimir operator for the adjoint representation of the gauge group $G$ and $T\left(R\right)$ is given by

$rT\left(R\right)=d\left(R\right)C_2\left(R\right),$(8.6)

with $C_2\left(R\right)$ is the value of the quadratic Casimir operator for the representation $R$ , $d\left(R\right)$ the dimension of the representation $R$ and $r$ the dimension (number of generators) of the group $G$ . For an $SU\left(N\right)$ group, $C_2\left(SU\right(N\left)\right)=N$ and $d=N^2-1$ , while for fermions transforming as the fundamental representation of $SU\left(N\right)$ with dimension $d\left(N\right)=N$ , the Casimir operator is $C_2\left(N\right)=\frac{N^2-1}{2N}$ so that $T\left(N\right)=\frac{1}{2}$ . In this case, the condition for asympotic freedom, Eq. (8.5) is

$\frac{n_g}{2}<\frac{11}{4}N,$(8.7)

which dictates that QCD with gauge group $SU\left(3\right)$ will be asympotically free, provided that there are less than $\frac{33}{2}$ quark flavors transforming as the fundamental representation. This condition is clearly satisfied by the currently observed six such flavors. On the other hand, $SU\left(3\right)$ Yang–Mills theory with more than two octets of fermions is not asymptotically free.

Note that an analogous running of the gauge coupling had previously been observed in quantum electrodynamics coupled to a charged vector field, by V. S. Vanyashin and M. V. Terent’ev [Reference Vanyashin and Terent’ev59] in 1965 and in pure Yang–Mills theory by I. Khriplovich [Reference Khriplovich60] in 1970 and G. ’t Hooft [61] in 1972, but its physical significance was not fully realized until the work of Gross, Wilczek and Politzer.

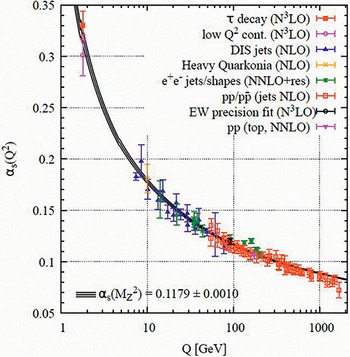
Figure 8.1 displays a plot of the observed running of the strong coupling ${\alpha }_s=\frac{g_3^2}{4\pi }$ as a function of probed energy for a wide range of processes and energy scales and its comparison to the QCD prediction. The agreement with the experiment results is well established and the running of the QCD coupling is quite apparent.

Figure 8.1 Summary of measurements [Reference Zyla, Barnett and Beringer62] of the running ${\alpha }_s$ as a function of the energy scale $Q$ . The agreement between the data and the QCD expectations is apparent. The order of QCD perturbation theory used in the extraction of ${\alpha }_s$ is indicated in brackets (NLO: next-to-leading order; NNLO: next-to-next-to-leading order; NNLO+res.: NNLO matched to a re-summed calculation; N ${}^3$ LO: next-to-NNLO).

The ramifications of asymptotic freedom were immediate and far reaching.Starting in 1968, SLAC began a series of experiments on the inelastic scattering of an electron from a proton: $e^{-}\left(\ell \right)+p\left(p\right)=e^{-}\left({\ell }^{\prime }\right)+X$ , where $X$ can be anything. Here ${\ell }^{\mu }\left({\ell }^{\prime \mu }\right)$ are the 4-momentum of the incident (final) electron and $p^{\mu }$ is the 4-momentum of the incident proton. Using general properties of Lorentz covariance and electric charge conservation, the differential cross for this inelastic process due to a single photon exchange in the rest frame of the incident proton where $p^{\mu }=(M,\vec{0})$ , ${\ell }^{\mu }=(E,\vec{\ell }),{\ell }^{\prime \mu }=(E^{\prime },\overrightarrow{{\ell }^{\prime }})$ and $\theta$ is the scattering angle between the initial and final state electrons takes the form

$\frac{d^2\sigma }{d{E}^{\prime }d\Omega }=\frac{{\alpha }_{EM}^2}{4E^2{sin}^4\left(\frac{\theta }{2}\right)}\frac{1}{\nu }\left(F_2(x,q^2){cos}^2\left(\frac{\theta }{2}\right)+\frac{2\nu }{M}{F}_1(x,q^2){sin}^2\left(\frac{\theta }{2}\right)\right).$(8.8)

Here $q^{\mu }=({\ell }^{\prime }-\ell {)}^{\mu }$ is the momentum transfer, $\nu =\frac{qp}{M}$ and $0<x=\frac{q^2}{2M\nu }<1$ . The $F_{1,2}(x,q^2)$ are the structure functions. In the rest frame, $\nu =E-E^{\prime }$ gives the electron energy loss.

It was observed [Reference Bloom, Coward and DeStaebler63; Reference Breidenbach, Friedman and Kendall64] (for a review, see [Reference Friedman and Kendall65]) that in the deep inelastic limit (sometimes referred to as the Bjorken limit) where $q^2,\nu \to \infty$ at fixed $x$ , the structure functions were independent of $q^2$ and dependent only on the dimensionless scaling variable $x$ so $F_{1,2}(x,q^2)=F_{1,2}\left(x\right)$ . This behavior was previously suggested by Bjorken [Reference Bjorken66] and is consistent with scattering off point-like constituents of the proton. Similar scaling behavior was also observed in deep inelastic muon- and neutrino-scattering experiments conducted at FNAL.

This scaling behavior could be accounted for by the parton model introduced by Feynman [Reference Feynman67],[Reference Feynman68] in his study of hadron–hadron collisions. The “naive” parton model describes the proton as a collection of point-like constituents called partons. At high momentum (“infinite momentum frame”) the partons are taken as free. Therefore, the interaction of one parton with the electron does not affect the other partons and this leads to scaling in $x$ . Today these partons are understood to be identical with the quarks postulated by Gell-Mann [Reference Gell-Mann69] in 1964 and independently by G. Zweig [Reference Zweig70]. The quark-parton model was successfully applied by Bjorken and Paschos [Reference Bjorken and Paschos71] to reproduce the observed scaling in deep inelastic electron-proton scattering. The observation of Bjorken scaling in deep inelastic scattering was instrumental in providing the first dynamical evidence of quarks and then gaining their acceptance as constituents of the proton. While the quark-parton model produced the scaling behavior observed at the time, the model itself lacked a firm theoretical foundation. It was not a quantum field theory and could not account for the strong interquark forces needed to account for the nonobservation of the partons in remnants of the collision. Due to its asympototic freedom, QCD interaction strength falls at large momentum transfers as $\frac{1}{\ell n{q}^2}$ and thus behaves in a manner similar to the parton model. In fact, in subsequent experiments, deviations from the exact scaling behavior of the structure functions appeared. The scaling violations were precisely detected in a muon scattering experiment at FNAL in 1975 [Reference Chang, Chen and Fox72]. The observed $q^2$ dependence of the structure functions was accurately accounted for by QCD as reviewed in [Reference Ellis73], marking a major success of the theory.

In a grander sense, the concept of asymptotic freedom provided a sensible interpretation of a quantum field theory at extreme ultraviolet energies. For nonasymptotically free theories, the running coupling increases with increasing energy diverging at the Landau poleFootnote ² [Reference Landau, Abrikosov and Khalatnikov74]. Asymptotic freedom in QCD also played an important role in theoretical work in early Universe cosmology. In the first few microseconds after the big bang, the Universe was comprised of a hot soup of quarks, leptons, gauge bosons and Higgs particles, which, as a consequence of asymptotic freedom, interacted very feebly and thus had properties amenable to calculation. This success in applying particle physics ideas to addressing puzzles in cosmology has led to a deep connection between the two disciplines, sometimes referred to as astroparticle physics, and has had a far-ranging influence on how one thinks about and treats cosmological problems. See [Reference Kolb and Turner75] for a readable introduction. Asymptotic freedom has also been displayed in a variety of condensed matter systems. For a discussion of various such systems, see, for example, reference [Reference Majorana151].

Motivated by the property of asymptotic freedom, it is suggestive that the attractive coupling grows at longer distances, leading to the confinement of all colored objects. Thus the quarks and gluons can never appear as physical states in the spectrum. Only net colored singlet hadrons (and glueballs) are physical states. Through the confinement mechanism, the potential long-range force that would naively arise from the massless gluons is obviated. This nonperturbative confinement mechanism has been demonstrated in lattice QCD [Reference Wilson77], which is a well-established nonperturbative approach to solving QCD. The lattice gauge theory is formulated on a grid or lattice of points in space and time. When the size of the lattice is taken infinitely large and its sites infinitesimally close to each other, the continuum QCD is recovered. Additional details can be found in [Reference Gattringer and Lang78–Reference Montvay and Münster80]. Lattice QCD has been used to compute the masses of the various hadrons as explicitly shown in reference [Reference Kronfeld81].

In the limit of massless up and down quarks, QCD exhibits the continuous global $SU(2{)}_V\times SU(2{)}_A$ chiral symmetry, which is dynamically broken to $SU(2{)}_V$ via the formation of a nonvanishing quark-antiquark vacuum condensate, which in turn gives mass to the nucleons. The pions are the pseudo Nambu–Goldstone bosons of the spontaneously broken axial $SU(2{)}_A$ . (The pions develop a small mass as a consequence of the up and down quark mass, which provides a small explicit breaking of the $SU(2{)}_A$ symmetry). Thus QCD automatically displays the global symmetry structure of the strong interactions.

QCD has been very well tested and proven highly successful [Reference Zyla, Barnett and Beringer62]. It constitutes one of the components of the Standard Model.

9 $SU(2{)}_L\times U(1)$ Invariant Lepton Couplings to the Electroweak Vectors

As we have seen, simply adding a vector mass term to the Lagrangian violates the gauge invariance. However, in 1962, J. Schwinger argued that the gauge invariance might not preclude a vector mass once the radiative corrections are included, provided the current coupling to the vector is sufficiently strong that it can create a massless pole in the current-current correlation function, $\Pi \left(q^2\right)$ . In that case, the full vector propagator varies as

$\frac{1}{q^2}\frac{1}{1-\Pi \left(q^2\right)}\to \frac{1}{q^2}\frac{1}{1+\frac{M_V^2}{q^2}}=\frac{1}{q^2+M_V^2},$(9.1)

which corresponds to a massive particle. The nonzero mass is said to be dynamically generated. While he was unable to demonstrate the existence of such a pole in any Lorentz-invariant model containing vectors in four space-time dimensions, he showed it was possible in a two space-time dimensional model, the Schwinger Model. In a very short, but extremely elegant paper [Reference Schwinger82], he studied a version of QED but in one space and one time dimension and with massless fermions. Since the fermions were massless, the QED ${}_2$ Lagrangian exhibits separate phase invariances for vector and axial vector transformations. Schwinger analytically solved the model and found a dynamically generated fermion-antifermion condensate that spontaneously breaks the axial symmetry and moreover the vacuum polarization function does indeed develop a massless pole so that the “photon” gets a nonvanishing mass. Although one can legitimately argue that the mass-generating mechanism is an artifact of the 1+1-dimensional nature of the model, this paper nonetheless was (and continues to be) extremely influential in that it showed that “vector” masses were possible in gauge theories.

A further elucidation of this idea was provided by P. Anderson [Reference Anderson83] in 1963 who argued that the gauging of the spontaneously broken global continuous $U\left(1\right)$ symmetry in BCS theory essentially leads to a massive vector photon, which was then unable to penetrate the superconductor (Meissner effect [Reference Meissner and Ochsenfeld84]). Here the massless pole is provided by the massless phonons mediating between the Cooper pairs in the superconductor. The model provided a mechanism for vector mass generation in a nonrelativistic setting. Much discussion in the literature followed regarding the general applicability of Anderson’s ideas to relativistic theories without any definitive resolution at the time.

Actually, there is an even earlier realization of the vector mass generation mechanism. In 1938, E. Stueckelberg [Reference Stueckelberg85] proposed a model of massive quantum electrodynamics using an additional scalar field that nonlinearly realized the symmetry. Like much of his work, it was well ahead of its time and largely ignored.

While the simple mimicking of QED by introducing vector bosons with direct mass terms was not an accurate description of the weak interactions, there was still considerable motivation for believing that the correct description should involve vector and axial vector fields. For one thing, the parity-violating extension of the Fermi theory was quite successful in describing low-energy, weak-interaction processes using lowest-order perturbation theory. A nice description of the phenomenological theory of the weak interactions before the advent of the electroweak gauge theory is contained in the monograph [Reference Källén86]. In addition, the Fermi description involved currents as did QED, albeit electric-charge-carrying currents that were both of a vector and an axial vector nature and moreover the hadronic piece of the vector current was conserved as is the vector current in QED. Finally, another property of the weak interactions where the resemblance to QED is striking is its universality [Reference Pontecorvo87],[Reference Puppi88]. That is, the weak processes of $\beta$ decay, muon decay and muon capture all had basically the same strength. This is reminiscent of the common magnitude of the electromagnetic charge of electrons, muons and protons.

J. Schwinger [Reference Schwinger40] was the first who attempted (unsuccessfully) to combine weak and electromagnetic interactions together in an $SU\left(2\right)$ Yang–Mills gauge theory using the charged massive $W^{\pm }$ and massless photons as the gauge vectors. His student S. Glashow [Reference Glashow89] and independently A. Salam and J. Ward [Reference Salam and Ward90] did arrive at a model of leptons based on the gauge group $SU(2{)}_L\times U(1)$ , which includes the correct couplings of the leptons to the electroweak gauge bosons. The model has two independent coupling constants $g_2,g_1$ associated with the $SU(2{)}_L$ and $U\left(1\right)$ gauge groups respectively. The product group has four generators and four associated vector bosons. To reproduce the V-A structure of charged weak interaction, the left-handed electron and its associated neutrino transform as a doublet, $L_L\left(x\right)=\left(\begin{array}{c}{\nu }_e\left(x\right)\\ e_L\left(x\right)\end{array}\right)$ , under $SU(2{)}_L$ , while the right-handed electron, $e_R\left(x\right)$ , is an $SU(2{)}_L$ singlet. Here we focus on the first generation of leptons consisting of the electron and its associated neutrino. The inclusion of the other lepton families is straightforward and will be discussed shortly. The model includes no right-handed neutrino field. To secure the couplings to the vector bosons, one follows the usual procedure of replacing ${\partial }_{\mu }{L}_L\left(x\right)\to D_{\mu }{L}_L$ and ${\partial }_{\mu }{e}_R\left(x\right)\to D_{\mu }{e}_R$ in the leptonic kinetic terms. Here the covariant derivatives are

$\begin{array}{cc}{D}_{\mu }{L}_L\left(x\right)& =\left({\partial }_{\mu }-i{g}_2\frac{{\sigma }_a}{2}{W}_{a_{\mu }}\left(x\right)+i{g}_1\frac{1}{2}{Y}_{\mu }\left(x\right)\right)L_L\left(x\right),\\ D_{\mu }{e}_R\left(x\right)& =({\partial }_{\mu }+i{g}_1{Y}_{\mu }\left(x\right))e_R\left(x\right),\end{array}$(9.2)

where ${\sigma }_a$ ; $a=1,2,3$ are the three Pauli matrices. The resultant locally invariant $SU(2{)}_L\times U(1)$ Lagrangian is

$L_e=-{\bar{L}}_L{\gamma }^{\mu }\frac{1}{i}{D}_{\mu }{L}_L-{\bar{e}}_R{\gamma }^{\mu }\frac{1}{i}{D}_{\mu }{e}_R.$(9.3)

The electron and its associated neutrino couplings to the gauge fields are thus dictated by the local $SU(2{)}_L\times U(1)$ invariance to be

$L_{{int}_e}=g_2{J}_{a_e}^{\mu }{W}_{{\mu }_a}+g_1{J}_{Y_e}^{\mu }{Y}_{\mu },$(9.4)

where the $SU(2{)}_L$ and $U\left(1\right)$ electron family currents are

$\begin{array}{cc}{J}_{a_e}^{\mu }& ={\bar{L}}_L{\gamma }^{\mu }\frac{{\sigma }_a}{2}{L}_L,\end{array}$(9.5)

$\begin{array}{cc}{J}_{Y_e}^{\mu }& =-\frac{1}{2}{\bar{L}}_L{\gamma }^{\mu }{L}_L-{\bar{e}}_R{\gamma }^{\mu }{e}_R.\end{array}$(9.6)

Two of the conserved currents of $SU(2{)}_L$ ,

$J_{{\pm }_e}^{\mu }=2(J_{1_e}^{\mu }\pm i{J}_{2_e}^{\mu }),$(9.7)

are identified with the weak-interaction charged currents, which couple to the associated vectors

$W_{\pm }^{\mu }=\frac{1}{\sqrt{2}}(W_1^{\mu }\pm i{W}_2^{\mu })$(9.8)

as

$L_{c{c}_e}=\frac{g_2}{2\sqrt{2}}\left(J_{{-}_e}^{\mu }{W}_{\mu +}+J_{{+}_e}^{\mu }{W}_{\mu -}\right).$(9.9)

There are two neutral generators: the third component $T_3$ of the weak isospin $SU(2{)}_L$ and the weak hypercharge generator $Y$ of the $U\left(1\right)$ . One combination is identified as the electric charge generator

$Q_{E{M}_e}=T_{3_e}+Y_e,$(9.10)

thus fixing the weak hypercharges with their values appearing in the covariant derivatives so that the electron has electric charge $-$ 1 and the neutrino is neutral.