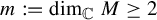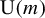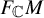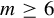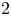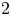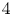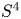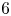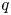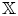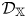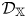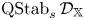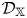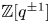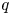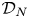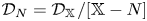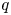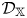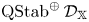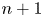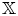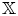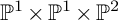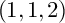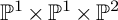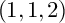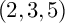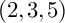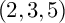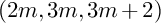56 results in 32Qxx
Strict positivity of Kähler–Einstein currents
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 27 May 2024, e68
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On divisorial stability of finite covers
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 22 May 2024, e65
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
K-stable smooth Fano threefolds of Picard rank two
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 20 March 2024, e41
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Positivity of Schur forms for strongly decomposably positive vector bundles
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 08 January 2024, e9
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Stability conditions for polarised varieties
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 20 November 2023, e104
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the ergodicity of unitary frame flows on Kähler manifolds
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 8 / August 2024
- Published online by Cambridge University Press:
- 16 October 2023, pp. 2143-2172
- Print publication:
- August 2024
-
- Article
- Export citation
K-stability of birationally superrigid Fano 3-fold weighted hypersurfaces
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 11 October 2023, e93
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Examples of dHYM connections in a variable background
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 02 October 2023, pp. 1-29
-
- Article
- Export citation
Realization of GKM fibrations and new examples of Hamiltonian non-Kähler actions
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 10 / October 2023
- Published online by Cambridge University Press:
- 24 August 2023, pp. 2149-2190
- Print publication:
- October 2023
-
- Article
- Export citation
q-stability conditions on Calabi–Yau-𝕏 categories
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 7 / July 2023
- Published online by Cambridge University Press:
- 07 June 2023, pp. 1347-1386
- Print publication:
- July 2023
-
- Article
- Export citation
K-STABLE DIVISORS IN
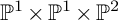 $\mathbb {P}^1\times \mathbb {P}^1\times \mathbb {P}^2$ OF DEGREE
$\mathbb {P}^1\times \mathbb {P}^1\times \mathbb {P}^2$ OF DEGREE 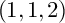 $(1,1,2)$
$(1,1,2)$
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 251 / September 2023
- Published online by Cambridge University Press:
- 28 April 2023, pp. 686-714
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Convergence of the gradient flow of renormalized volume to convex cores with totally geodesic boundary
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 4 / April 2023
- Published online by Cambridge University Press:
- 04 April 2023, pp. 830-859
- Print publication:
- April 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The existence of the Kähler–Ricci soliton degeneration
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 11 / 2023
- Published online by Cambridge University Press:
- 10 March 2023, e9
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
LINES ON HOLOMORPHIC CONTACT MANIFOLDS AND A GENERALIZATION OF
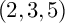 $(2,3,5)$-DISTRIBUTIONS TO HIGHER DIMENSIONS
$(2,3,5)$-DISTRIBUTIONS TO HIGHER DIMENSIONS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 251 / September 2023
- Published online by Cambridge University Press:
- 23 February 2023, pp. 652-668
- Print publication:
- September 2023
-
- Article
- Export citation
Second-order estimates for collapsed limits of Ricci-flat Kähler metrics
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 05 January 2023, pp. 912-926
- Print publication:
- September 2023
-
- Article
- Export citation
Pseudo-holomorphic dynamics in the restricted three-body problem
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 174 / Issue 3 / May 2023
- Published online by Cambridge University Press:
- 05 December 2022, pp. 663-693
- Print publication:
- May 2023
-
- Article
- Export citation
Smooth hypersurfaces in abelian varieties over arithmetic rings
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 28 October 2022, e97
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
K-stability of Fano varieties via admissible flags
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 10 / 2022
- Published online by Cambridge University Press:
- 30 June 2022, e15
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A note on holomorphic sectional curvature of a hermitian manifold
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 64 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 04 March 2022, pp. 739-745
- Print publication:
- September 2022
-
- Article
- Export citation
Almost existence from the feral perspective and some questions
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 2 / February 2022
- Published online by Cambridge University Press:
- 10 June 2021, pp. 792-834
- Print publication:
- February 2022
-
- Article
- Export citation

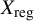
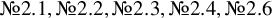 and
and 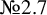 are K-stable, and we also prove that smooth Fano threefolds in the family
are K-stable, and we also prove that smooth Fano threefolds in the family 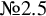 that satisfy one very explicit generality condition are K-stable.
that satisfy one very explicit generality condition are K-stable.