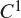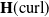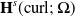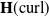158 results in 65Nxx
Adaptive finite element methods
- Part of
-
- Journal:
- Acta Numerica / Volume 33 / July 2024
- Published online by Cambridge University Press:
- 04 September 2024, pp. 163-485
- Print publication:
- July 2024
-
- Article
-
- You have access
- Open access
- Export citation
A finite-volume scheme for fractional diffusion on bounded domains
- Part of
-
- Journal:
- European Journal of Applied Mathematics , First View
- Published online by Cambridge University Press:
- 16 April 2024, pp. 1-21
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
NUMERICAL SIMULATIONS FOR LARGELY DEFORMED BEAMS AND RINGS ADOPTING A NONTENSILE SMOOTHED PARTICLE HYDRODYNAMICS ALGORITHM
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 64 / Issue 4 / October 2022
- Published online by Cambridge University Press:
- 15 August 2023, pp. 355-379
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The virtual element method
- Part of
-
- Journal:
- Acta Numerica / Volume 32 / May 2023
- Published online by Cambridge University Press:
- 11 May 2023, pp. 123-202
- Print publication:
- May 2023
-
- Article
-
- You have access
- Open access
- Export citation
Low-rank tensor methods for partial differential equations
- Part of
-
- Journal:
- Acta Numerica / Volume 32 / May 2023
- Published online by Cambridge University Press:
- 11 May 2023, pp. 1-121
- Print publication:
- May 2023
-
- Article
-
- You have access
- Open access
- Export citation
A LOCAL PROJECTION STABILIZATION FOR CONVECTION–DIFFUSION–REACTION EQUATIONS USING BIORTHOGONAL SYSTEMS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 64 / Issue 3 / July 2022
- Published online by Cambridge University Press:
- 20 February 2023, pp. 205-226
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Solving two-dimensional H(curl)-elliptic interface systems with optimal convergence on unfitted meshes
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 34 / Issue 4 / August 2023
- Published online by Cambridge University Press:
- 05 January 2023, pp. 774-805
-
- Article
- Export citation
A COMPREHENSIVE STUDY OF OPTION PRICING WITH TRANSACTION COSTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 3 / December 2022
- Published online by Cambridge University Press:
- 22 August 2022, pp. 522-524
- Print publication:
- December 2022
-
- Article
-
- You have access
- HTML
- Export citation
ELECTRICAL IMPEDANCE TOMOGRAPHY USING NONCONFORMING MESH AND POSTERIOR APPROXIMATED REGRESSION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 03 March 2022, pp. 520-522
- Print publication:
- June 2022
-
- Article
-
- You have access
- HTML
- Export citation
A REVIEW OF ONE-PHASE HELE-SHAW FLOWS AND A LEVEL-SET METHOD FOR NONSTANDARD CONFIGURATIONS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 63 / Issue 3 / July 2021
- Published online by Cambridge University Press:
- 23 September 2021, pp. 269-307
-
- Article
- Export citation
OPTIMAL CONTROL OF THE DECUMULATION OF A RETIREMENT PORTFOLIO WITH VARIABLE SPENDING AND DYNAMIC ASSET ALLOCATION
- Part of
-
- Journal:
- ASTIN Bulletin: The Journal of the IAA / Volume 51 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 28 July 2021, pp. 905-938
- Print publication:
- September 2021
-
- Article
- Export citation
Mass-conserving diffusion-based dynamics on graphs
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 33 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 14 April 2021, pp. 423-471
-
- Article
-
- You have access
- Open access
- Export citation
Mean-field models for segregation dynamics
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 33 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 23 December 2020, pp. 111-132
-
- Article
- Export citation
ADAPTIVE GRID REFINEMENT USING THE GENERALISED FINITE-DIFFERENCE METHOD
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 11 September 2020, p. 349
- Print publication:
- April 2021
-
- Article
-
- You have access
- Export citation
FINITE-ELEMENT METHODS AND MULTI-FIELD APPLICATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 1 / August 2020
- Published online by Cambridge University Press:
- 20 May 2020, pp. 174-176
- Print publication:
- August 2020
-
- Article
-
- You have access
- Export citation
A MODIFIED IMMERSED FINITE VOLUME ELEMENT METHOD FOR ELLIPTIC INTERFACE PROBLEMS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 62 / Issue 1 / January 2020
- Published online by Cambridge University Press:
- 13 May 2020, pp. 42-61
-
- Article
- Export citation
NUMERICAL INVESTIGATION AND APPLICATION OF FRACTIONAL DYNAMICAL SYSTEMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 23 October 2019, pp. 163-165
- Print publication:
- February 2020
-
- Article
-
- You have access
- Export citation
Scattering coefficients of inhomogeneous objects and their application in target classification in wave imaging
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 31 / Issue 4 / August 2020
- Published online by Cambridge University Press:
- 03 July 2019, pp. 553-573
-
- Article
- Export citation
Minimal convex extensions and finite difference discretisation of the quadratic Monge–Kantorovich problem
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 30 / Issue 6 / December 2019
- Published online by Cambridge University Press:
- 21 September 2018, pp. 1041-1078
-
- Article
- Export citation
CALCULATION OF CRITICAL PARAMETERS FOR SPONTANEOUS COMBUSTION FOR SOME COMPLEX GEOMETRIES USING AN INDIRECT NUMERICAL METHOD
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 59 / Issue 3 / January 2018
- Published online by Cambridge University Press:
- 26 February 2018, pp. 402-412
-
- Article
-
- You have access
- Export citation