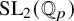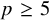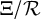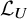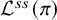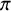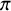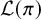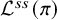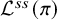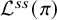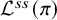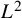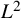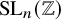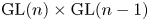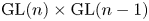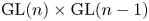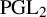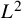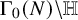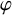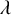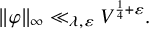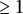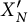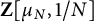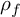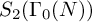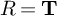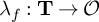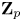540 results in 11Fxx
DISCREPANCY BOUNDS FOR THE DISTRIBUTION OF RANKIN–SELBERG L-FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 18 October 2024, pp. 1-11
-
- Article
-
- You have access
- HTML
- Export citation
PARITY OF CONJUGATE SELF-DUAL REPRESENTATIONS OF INNER FORMS OF
 $\operatorname { {GL}}_n$ OVER p-ADIC FIELDS
$\operatorname { {GL}}_n$ OVER p-ADIC FIELDS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu , First View
- Published online by Cambridge University Press:
- 20 September 2024, pp. 1-23
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Stability in the category of smooth mod-p representations of
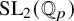 ${\mathrm {SL}}_2(\mathbb {Q}_p)$
${\mathrm {SL}}_2(\mathbb {Q}_p)$
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 09 September 2024, e77
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Local parameters of supercuspidal representations
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 12 / 2024
- Published online by Cambridge University Press:
- 09 September 2024, e13
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the local
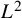 $L^2$-Bound of the Eisenstein series
$L^2$-Bound of the Eisenstein series
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 06 September 2024, e76
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Cyclic base change of cuspidal automorphic representations over function fields
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 9 / September 2024
- Published online by Cambridge University Press:
- 11 September 2024, pp. 1959-2004
- Print publication:
- September 2024
-
- Article
-
- You have access
- HTML
- Export citation
On the Gross–Prasad conjecture with its refinement for (SO(5), SO(2)) and the generalized Böcherer conjecture
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 9 / September 2024
- Published online by Cambridge University Press:
- 13 September 2024, pp. 2115-2202
- Print publication:
- September 2024
-
- Article
-
- You have access
- HTML
- Export citation
Period relations for Rankin–Selberg convolutions for
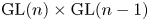 ${\mathrm {GL}}(n)\times {\mathrm {GL}}(n-1)$
${\mathrm {GL}}(n)\times {\mathrm {GL}}(n-1)$
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 8 / August 2024
- Published online by Cambridge University Press:
- 11 September 2024, pp. 1871-1915
- Print publication:
- August 2024
-
- Article
-
- You have access
- HTML
- Export citation
Differential forms on universal K3 surfaces
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society , First View
- Published online by Cambridge University Press:
- 12 July 2024, pp. 1-9
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ARITHMETIC PROPERTIES OF AN ANALOGUE OF t-CORE PARTITIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 03 June 2024, pp. 1-12
-
- Article
-
- You have access
- HTML
- Export citation
L-invariants for cohomological representations of PGL(2) over arbitrary number fields
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 30 May 2024, e71
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Theta functions, fourth moments of eigenforms and the sup-norm problem II
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 12 / 2024
- Published online by Cambridge University Press:
- 30 May 2024, e11
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
TWISTED GAN–GROSS–PRASAD CONJECTURE FOR CERTAIN TEMPERED L-PACKETS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu , First View
- Published online by Cambridge University Press:
- 24 May 2024, pp. 1-23
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ARCHIMEDEAN NEWFORM THEORY FOR
 $\operatorname {\mathrm {GL}}_n$
$\operatorname {\mathrm {GL}}_n$
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu , First View
- Published online by Cambridge University Press:
- 17 May 2024, pp. 1-76
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The Heisenberg covering of the Fermat curve
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 10 May 2024, pp. 1-27
-
- Article
-
- You have access
- HTML
- Export citation
NORMAL BASES FOR FUNCTION FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 1 / August 2024
- Published online by Cambridge University Press:
- 06 May 2024, pp. 44-55
- Print publication:
- August 2024
-
- Article
-
- You have access
- HTML
- Export citation
WILES DEFECT OF HECKE ALGEBRAS VIA LOCAL-GLOBAL ARGUMENTS: WITH AN APPENDIX BY NAJMUDDIN FAKHRUDDIN AND CHANDRASHEKHAR B. KHARE
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu , First View
- Published online by Cambridge University Press:
- 25 April 2024, pp. 1-81
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Completed prismatic F-crystals and crystalline Zp-local systems
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 5 / May 2024
- Published online by Cambridge University Press:
- 18 April 2024, pp. 1101-1166
- Print publication:
- May 2024
-
- Article
-
- You have access
- HTML
- Export citation
ON THE DISTINCTION OF IWAHORI-SPHERICAL DISCRETE SERIES REPRESENTATIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu , First View
- Published online by Cambridge University Press:
- 17 April 2024, pp. 1-15
-
- Article
-
- You have access
- HTML
- Export citation
Summation formulae of multiplicative functions over arithmetic progressions and applications
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 12 April 2024, pp. 1-28
-
- Article
-
- You have access
- HTML
- Export citation