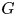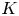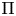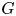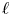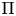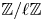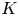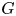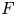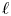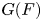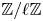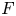1. Introduction
A particular case of Langlands’ principle of functoriality is cyclic base change, which has been established in significant generality over global fields of characteristic ![]() $0$, but not global fields of characteristic
$0$, but not global fields of characteristic ![]() $p$. The results towards cyclic base change functoriality in characteristic 0 were worked out in a long series of papers by many authors, including Saito, Shintani, Langlands, Arthur, Clozel, Labesse, and Harris (see the introduction to [Reference FengFen24] for references), all following a strategy proposed by Langlands that is based on studying the twisted trace formula. But this strategy encounters complications in characteristic
$p$. The results towards cyclic base change functoriality in characteristic 0 were worked out in a long series of papers by many authors, including Saito, Shintani, Langlands, Arthur, Clozel, Labesse, and Harris (see the introduction to [Reference FengFen24] for references), all following a strategy proposed by Langlands that is based on studying the twisted trace formula. But this strategy encounters complications in characteristic ![]() $p$, for example because of the contribution of inseparable elements to the trace formula.
$p$, for example because of the contribution of inseparable elements to the trace formula.
In this paper we establish (under technical assumptions) cyclic base change liftings over characteristic-![]() $p$ global fields, using a completely different strategy that is instead predicated upon the theory of automorphy lifting. Furthermore, we prove novel types of results regarding cyclic base change in the Genestier–Lafforgue correspondence. The results and proofs will be described in more detail in the rest of this introduction.
$p$ global fields, using a completely different strategy that is instead predicated upon the theory of automorphy lifting. Furthermore, we prove novel types of results regarding cyclic base change in the Genestier–Lafforgue correspondence. The results and proofs will be described in more detail in the rest of this introduction.
1.1 Global base change
Let ![]() $X$ be a smooth, projective, geometrically connected curve over the finite field
$X$ be a smooth, projective, geometrically connected curve over the finite field ![]() ${\mathbb {F}}_q$ with function field
${\mathbb {F}}_q$ with function field ![]() $K := {\mathbb {F}}_q(X)$, and let
$K := {\mathbb {F}}_q(X)$, and let ![]() $G$ be a split semisimple algebraic group over
$G$ be a split semisimple algebraic group over ![]() ${\mathbb {F}}_q$. Let
${\mathbb {F}}_q$. Let ![]() $\Pi$ be a cuspidal automorphic representation of
$\Pi$ be a cuspidal automorphic representation of ![]() $G(\mathbb {A}_K)$ defined over a number field.Footnote 1 For a field extension
$G(\mathbb {A}_K)$ defined over a number field.Footnote 1 For a field extension ![]() $K'/K$, a (weak) base change lifting of
$K'/K$, a (weak) base change lifting of ![]() $\Pi$ to
$\Pi$ to ![]() $K'$ is a cuspidal automorphic representation
$K'$ is a cuspidal automorphic representation ![]() $\Pi '$ of
$\Pi '$ of ![]() $G(\mathbb {A}_{K'})$ such that for almost all places
$G(\mathbb {A}_{K'})$ such that for almost all places ![]() $v$ of
$v$ of ![]() $K$ where
$K$ where ![]() $\Pi$ is unramified,
$\Pi$ is unramified, ![]() $\Pi '$ is also unramified at all places of
$\Pi '$ is also unramified at all places of ![]() $K'$ above
$K'$ above ![]() $v$, and the Satake parameters of
$v$, and the Satake parameters of ![]() $\Pi$ and of
$\Pi$ and of ![]() $\Pi '$ over
$\Pi '$ over ![]() $v$ are related by the base change homomorphism for spherical Hecke algebras. (Later in the paper we will define and prove stronger notions of base change lifting.)
$v$ are related by the base change homomorphism for spherical Hecke algebras. (Later in the paper we will define and prove stronger notions of base change lifting.)
Over number fields, the existence of such a base change lifting is proved in complete generality for cuspidal automorphic representations of ![]() $\operatorname {GL}_n$ [Reference Arthur and ClozelAC89], and it is proved under some technical assumptions by Labesse [Reference LabesseLab99] for general groups, still over number fields, by a comparison of the stable trace formula for
$\operatorname {GL}_n$ [Reference Arthur and ClozelAC89], and it is proved under some technical assumptions by Labesse [Reference LabesseLab99] for general groups, still over number fields, by a comparison of the stable trace formula for ![]() $G({\mathbb {A}}_{K})$ with the stable trace formula for
$G({\mathbb {A}}_{K})$ with the stable trace formula for ![]() $G({\mathbb {A}}_{K'})$ twisted with respect to a generator of
$G({\mathbb {A}}_{K'})$ twisted with respect to a generator of ![]() $\operatorname {Gal}(K'/K)$. It is expected that the stable trace formula will eventually provide weak base change over function fields as well, but the proof of such a formula faces a number of obstacles and even the first steps of the proof of the general trace formula are only now becoming available [Reference Labesse and LemaireLL21].
$\operatorname {Gal}(K'/K)$. It is expected that the stable trace formula will eventually provide weak base change over function fields as well, but the proof of such a formula faces a number of obstacles and even the first steps of the proof of the general trace formula are only now becoming available [Reference Labesse and LemaireLL21].
In this paper we take a different approach to establish the existence of weak base change liftings (under technical hypotheses), based on automorphy lifting arguments instead of the trace formula. In particular, we use the results of Vincent Lafforgue on the global Langlands correspondence [Reference LafforgueLaf18]. Let ![]() ${\widehat {G}}$ denote the dual group of
${\widehat {G}}$ denote the dual group of ![]() $G$, considered as a split semisimple group scheme over
$G$, considered as a split semisimple group scheme over ![]() ${\mathbb {Z}}$. For each prime
${\mathbb {Z}}$. For each prime ![]() $\ell$ we fix an algebraic closure
$\ell$ we fix an algebraic closure ![]() $\overline {{\mathbb {Q}}}_\ell$ of
$\overline {{\mathbb {Q}}}_\ell$ of ![]() ${\mathbb {Q}}_\ell$. A consequence of V. Lafforgue's work in [Reference LafforgueLaf18] is the construction, for each cuspidal automorphic representation
${\mathbb {Q}}_\ell$. A consequence of V. Lafforgue's work in [Reference LafforgueLaf18] is the construction, for each cuspidal automorphic representation ![]() $\Pi$ of
$\Pi$ of ![]() $G(\mathbb {A}_K)$ valued in
$G(\mathbb {A}_K)$ valued in ![]() $\overline {\mathbb {Q}}_{\ell }$, of a finite set of
$\overline {\mathbb {Q}}_{\ell }$, of a finite set of ![]() ${\widehat {G}}(\overline {\mathbb {Q}}_{\ell })$-conjugacy classes of continuous Galois representations
${\widehat {G}}(\overline {\mathbb {Q}}_{\ell })$-conjugacy classes of continuous Galois representations ![]() $\sigma : \operatorname {Gal}(K^{\rm s}/K) \to {\widehat {G}}(\overline {\mathbb {Q}}_{\ell })$, each of which has the property that its Frobenius eigenvalues at unramified places match the Satake parameters of
$\sigma : \operatorname {Gal}(K^{\rm s}/K) \to {\widehat {G}}(\overline {\mathbb {Q}}_{\ell })$, each of which has the property that its Frobenius eigenvalues at unramified places match the Satake parameters of ![]() $\Pi$ (see § 4 for the precise formulation).
$\Pi$ (see § 4 for the precise formulation).
Suppose ![]() $\Pi$ is a cuspidal automorphic representation defined over
$\Pi$ is a cuspidal automorphic representation defined over ![]() $\overline {\mathbb {Q}}$. Then for each
$\overline {\mathbb {Q}}$. Then for each ![]() $\ell \neq p$, we may choose an embedding
$\ell \neq p$, we may choose an embedding ![]() $\overline {\mathbb {Q}} \hookrightarrow \overline {\mathbb {Q}}_{\ell }$, and then apply Lafforgue's theory, obtaining as above a finite set of Galois representations. These will be referred to as the Galois representations ‘attached to
$\overline {\mathbb {Q}} \hookrightarrow \overline {\mathbb {Q}}_{\ell }$, and then apply Lafforgue's theory, obtaining as above a finite set of Galois representations. These will be referred to as the Galois representations ‘attached to ![]() $\Pi$ by Lafforgue's correspondence.’ A consequence of our main result is the following theorem.
$\Pi$ by Lafforgue's correspondence.’ A consequence of our main result is the following theorem.
Theorem 1.1 Let ![]() $\Pi$ be a cuspidal automorphic representation of
$\Pi$ be a cuspidal automorphic representation of ![]() $G(\mathbb {A}_K)$ over
$G(\mathbb {A}_K)$ over ![]() $\overline {\mathbb {Q}}$. Suppose that for some (equivalently, any) prime
$\overline {\mathbb {Q}}$. Suppose that for some (equivalently, any) prime ![]() $\ell ' \neq p$, some (equivalently, each) of the Galois representations attached to
$\ell ' \neq p$, some (equivalently, each) of the Galois representations attached to ![]() $\Pi$ by Lafforgue's correspondence has Zariski dense image in
$\Pi$ by Lafforgue's correspondence has Zariski dense image in ![]() $\widehat {G}$. Then there exists a constant
$\widehat {G}$. Then there exists a constant ![]() $c(\Pi )$ such that for all primes
$c(\Pi )$ such that for all primes ![]() $\ell > c(\Pi )$, and all cyclic
$\ell > c(\Pi )$, and all cyclic ![]() $\ell$-extensions
$\ell$-extensions ![]() $K'/K$, there is a weak base change lifting of
$K'/K$, there is a weak base change lifting of ![]() $\Pi$ to a cuspidal automorphic representation
$\Pi$ to a cuspidal automorphic representation ![]() $\Pi '$ of
$\Pi '$ of ![]() $G(\mathbb {A}_{K'})$.
$G(\mathbb {A}_{K'})$.
This follows from a more precise and refined result, Theorem 6.3, which guarantees that ![]() $\Pi '$ may be chosen to be a base change lifting in the strongest possible sense (including a compatibility at ramified places). However, the latter requires more discussion in order to formulate, so we postpone it for now.
$\Pi '$ may be chosen to be a base change lifting in the strongest possible sense (including a compatibility at ramified places). However, the latter requires more discussion in order to formulate, so we postpone it for now.
Remark 1.2 In [Reference Sawin and TemplierST21], the Ramanujan conjecture is proved for cuspidal automorphic representations satisfying certain types of local conditions, conditionally upon the existence of base change liftings (with compatibility at ramified places as well) for constant extensions of large enough degree. Our Theorem 6.3 provides this type of base change lifting. However, it is not hard to deduce the Ramanujan conjecture directly when our hypothesis is satisfied.
We sketch the approach of the proof. It is based on the automorphy lifting techniques pioneered by Taylor and Wiles. The first ingredient in this program is residual automorphy, and this is provided by [Reference FengFen24], which established the existence of base change for automorphic forms over ![]() $\overline {\mathbb {F}}_{\ell }$ in the special case where the extension
$\overline {\mathbb {F}}_{\ell }$ in the special case where the extension ![]() $K'/K$ is cyclic of order
$K'/K$ is cyclic of order ![]() $\ell$. (It was essential for the argument of [Reference FengFen24] that the characteristic
$\ell$. (It was essential for the argument of [Reference FengFen24] that the characteristic ![]() $\ell$ of the automorphic forms coincides with the order
$\ell$ of the automorphic forms coincides with the order ![]() $\ell$ of the extension.) To prove Theorem 1.1, we use compatible systems of Galois representations (whose existence is guaranteed by the Zariski density assumption) to bootstrap from this case and lift the automorphy to characteristic
$\ell$ of the extension.) To prove Theorem 1.1, we use compatible systems of Galois representations (whose existence is guaranteed by the Zariski density assumption) to bootstrap from this case and lift the automorphy to characteristic ![]() $0$. In particular, we prove an automorphy lifting theorem for representations with arbitrary ramification, going beyond the everywhere unramified case which was established by four of the authors in [Reference Böckle, Harris, Khare and ThorneBHKT19].
$0$. In particular, we prove an automorphy lifting theorem for representations with arbitrary ramification, going beyond the everywhere unramified case which was established by four of the authors in [Reference Böckle, Harris, Khare and ThorneBHKT19].
We briefly discuss some of the new issues that go into proving this ramified automorphy lifting result. First, we need to arrange local deformation rings that are well behaved, which is one reason for requiring ![]() $\ell > c(\Pi )$. We show that such a condition guarantees that the unrestricted local deformation condition is smooth (see § 5 for discussion of this). A second issue is that we need to know that the image of the associated
$\ell > c(\Pi )$. We show that such a condition guarantees that the unrestricted local deformation condition is smooth (see § 5 for discussion of this). A second issue is that we need to know that the image of the associated ![]() $\ell$-adic Galois representation is large enough to provide a sufficient supply of Taylor–Wiles primes, for all
$\ell$-adic Galois representation is large enough to provide a sufficient supply of Taylor–Wiles primes, for all ![]() $\ell > c(\Pi )$. The condition used in [Reference Böckle, Harris, Khare and ThorneBHKT19] is that the image is
$\ell > c(\Pi )$. The condition used in [Reference Böckle, Harris, Khare and ThorneBHKT19] is that the image is ![]() ${\widehat {G}}$-abundant. For the ‘potential automorphy’ theorem of [Reference Böckle, Harris, Khare and ThorneBHKT19], it was enough to know that the image mod
${\widehat {G}}$-abundant. For the ‘potential automorphy’ theorem of [Reference Böckle, Harris, Khare and ThorneBHKT19], it was enough to know that the image mod ![]() $\ell$ is abundant outside a set of
$\ell$ is abundant outside a set of ![]() $\ell$ having Dirichlet density 0. Since the
$\ell$ having Dirichlet density 0. Since the ![]() $\ell$-adic image is Zariski dense, this follows from a result of Larsen [Reference LarsenLar95]. In order to obtain base change liftings for
$\ell$-adic image is Zariski dense, this follows from a result of Larsen [Reference LarsenLar95]. In order to obtain base change liftings for ![]() $\ell > c(\Pi )$, we need the stronger result that the image mod
$\ell > c(\Pi )$, we need the stronger result that the image mod ![]() $\ell$ is abundant for all but finitely many
$\ell$ is abundant for all but finitely many ![]() $\ell$. For this we use a recent theorem proved by one of us with Gajda and Petersen [Reference Böckle, Gajda and PetersenBGP19]; see also [Reference DrinfeldDri18, E.10].
$\ell$. For this we use a recent theorem proved by one of us with Gajda and Petersen [Reference Böckle, Gajda and PetersenBGP19]; see also [Reference DrinfeldDri18, E.10].
1.2 Local base change
From Theorem 1.1 we draw some applications to the local Langlands correspondence. To state them, let ![]() $F$ be a local function field of characteristic
$F$ be a local function field of characteristic ![]() $p$,
$p$, ![]() $W_F$ the Weil group of
$W_F$ the Weil group of ![]() $F$, and
$F$, and ![]() $G$ a split semisimple group over
$G$ a split semisimple group over ![]() $F$. Genestier and Lafforgue [Reference Genestier and LafforgueGL17] have constructed a semisimplified local Langlands correspondence
$F$. Genestier and Lafforgue [Reference Genestier and LafforgueGL17] have constructed a semisimplified local Langlands correspondence
If ![]() $F'/F$ is a field extension, we say that an irreducible admissible representation
$F'/F$ is a field extension, we say that an irreducible admissible representation ![]() $\pi '$ of
$\pi '$ of ![]() $G(F')$ is a base change lifting of an irreducible admissible representation
$G(F')$ is a base change lifting of an irreducible admissible representation ![]() $\pi$ of
$\pi$ of ![]() $G(F)$ if
$G(F)$ if ![]() $\sigma _{\pi '} \cong \sigma _{\pi }|_{W_{F'}}$.
$\sigma _{\pi '} \cong \sigma _{\pi }|_{W_{F'}}$.
Using our global results, we deduce in § 7 the following theorem.
Theorem 1.3 Let ![]() $\pi$ be an irreducible admissible representation of
$\pi$ be an irreducible admissible representation of ![]() $G(F)$ over
$G(F)$ over ![]() $\overline {\mathbb {Q}}$. There exists a constant
$\overline {\mathbb {Q}}$. There exists a constant ![]() $c(\pi )$ such that for all primes
$c(\pi )$ such that for all primes ![]() $\ell > c(\pi )$, for any
$\ell > c(\pi )$, for any ![]() $\mathbb {Z}/\ell \mathbb {Z}$-extension
$\mathbb {Z}/\ell \mathbb {Z}$-extension ![]() $F'/F$ there exists a base change lifting of
$F'/F$ there exists a base change lifting of ![]() $\pi \otimes _{\overline {\mathbb {Q}}} \overline {\mathbb {Q}}_{\ell }$ to
$\pi \otimes _{\overline {\mathbb {Q}}} \overline {\mathbb {Q}}_{\ell }$ to ![]() $G(F')$.
$G(F')$.
An analogous theorem was proved for mod ![]() $\ell$ representations, when
$\ell$ representations, when ![]() $F'/F$ is cyclic of degree
$F'/F$ is cyclic of degree ![]() $\ell$, in [Reference FengFen24]. The strategy here is completely different. The idea is to globalize
$\ell$, in [Reference FengFen24]. The strategy here is completely different. The idea is to globalize ![]() $\pi$ to a cuspidal automorphic representation
$\pi$ to a cuspidal automorphic representation ![]() $\Pi$, and the extension
$\Pi$, and the extension ![]() $F'/F$ to a global extension
$F'/F$ to a global extension ![]() $K'/K$, to which we can apply Theorem 1.1. If we can do this, then we can extract the local component of
$K'/K$, to which we can apply Theorem 1.1. If we can do this, then we can extract the local component of ![]() $\Pi '$ to obtain a local base change
$\Pi '$ to obtain a local base change ![]() $\pi '$. However, we must take care to construct a globalization
$\pi '$. However, we must take care to construct a globalization ![]() $\Pi$ satisfying the hypotheses of Theorem 1.1. This is accomplished by setting up
$\Pi$ satisfying the hypotheses of Theorem 1.1. This is accomplished by setting up ![]() $\Pi$ with specified local conditions at a finite number of auxiliary places, so that the corresponding Galois representation
$\Pi$ with specified local conditions at a finite number of auxiliary places, so that the corresponding Galois representation ![]() $\sigma _{\Pi }$ has Zariski dense image. For example, we put a supercuspidal local component ‘
$\sigma _{\Pi }$ has Zariski dense image. For example, we put a supercuspidal local component ‘![]() $V_{\phi }$’ at one auxiliary place whose Genestier–Lafforgue parameter
$V_{\phi }$’ at one auxiliary place whose Genestier–Lafforgue parameter ![]() $\sigma _{V_{\phi }}$ is already absolutely irreducible, in order to guarantee that
$\sigma _{V_{\phi }}$ is already absolutely irreducible, in order to guarantee that ![]() $\sigma _{\Pi }$ is absolutely irreducible. For this, we require knowledge of
$\sigma _{\Pi }$ is absolutely irreducible. For this, we require knowledge of ![]() $\sigma _{V_{\phi }}$. This is obtained by finding a different globalization
$\sigma _{V_{\phi }}$. This is obtained by finding a different globalization ![]() $\Pi ^{\mathrm {aux}}$ of
$\Pi ^{\mathrm {aux}}$ of ![]() $V_{\phi }$ whose corresponding global Galois representation
$V_{\phi }$ whose corresponding global Galois representation ![]() $\sigma _{\Pi ^{\mathrm {aux}}}$ can be calculated explicitly, from which we extract the Genestier–Lafforgue parameter of
$\sigma _{\Pi ^{\mathrm {aux}}}$ can be calculated explicitly, from which we extract the Genestier–Lafforgue parameter of ![]() $V_{\phi }$ using local–global compatibility; the work of Heinloth, Ngô, and Yun [Reference Heinloth, Ngô and YunHNY13] provides a convenient such ‘auxiliary globalization.’
$V_{\phi }$ using local–global compatibility; the work of Heinloth, Ngô, and Yun [Reference Heinloth, Ngô and YunHNY13] provides a convenient such ‘auxiliary globalization.’
In the final section § 8, we study local base change more explicitly for a class of supercuspidal representations singled out in [Reference KalethaKal19] under the name ‘toral supercuspidal representations.’ This is a fairly broad class of supercuspidal representations, encompassing examples of arbitrary depth, for which Kaletha has constructed in [Reference KalethaKal19, § 6] an explicit parametrization by ![]() $L$-parameters, satisfying good properties of the expected local Langlands correspondence. The ‘Howe-unramified’ toral supercuspidal representations have been studied further by Chan and Oi [Reference Chan and OiCO23] (noting that the ‘toral representations’ of [Reference KalethaKal19] are described as ‘0-toral’ in [Reference Chan and OiCO23] (see, in particular, [Reference Chan and OiCO23, § 8])—we follow the terminology of [Reference Chan and OiCO23] in the body of this paper). For the representations studied in [Reference Chan and OiCO23], we are able to explicitly characterize unramified base change along the Genestier–Lafforgue correspondence under some technical assumptions. A motivation behind the results of § 8 is consistency between Kaletha's parametrization and the Genestier–Lafforgue correspondence. Roughly speaking, we prove, under genericity conditions, that the base change of mod
$L$-parameters, satisfying good properties of the expected local Langlands correspondence. The ‘Howe-unramified’ toral supercuspidal representations have been studied further by Chan and Oi [Reference Chan and OiCO23] (noting that the ‘toral representations’ of [Reference KalethaKal19] are described as ‘0-toral’ in [Reference Chan and OiCO23] (see, in particular, [Reference Chan and OiCO23, § 8])—we follow the terminology of [Reference Chan and OiCO23] in the body of this paper). For the representations studied in [Reference Chan and OiCO23], we are able to explicitly characterize unramified base change along the Genestier–Lafforgue correspondence under some technical assumptions. A motivation behind the results of § 8 is consistency between Kaletha's parametrization and the Genestier–Lafforgue correspondence. Roughly speaking, we prove, under genericity conditions, that the base change of mod ![]() $\ell$ toral supercuspidal representations along unramified
$\ell$ toral supercuspidal representations along unramified ![]() $\mathbb {Z}/\ell \mathbb {Z}$-extensions, under the Genestier–Lafforgue correspondence, behaves as would be predicted by Kaletha's parametrization. See § 8.4 for the precise formulations.
$\mathbb {Z}/\ell \mathbb {Z}$-extensions, under the Genestier–Lafforgue correspondence, behaves as would be predicted by Kaletha's parametrization. See § 8.4 for the precise formulations.
Next we comment on the proof. The mechanism for understanding base change of mod ![]() $\ell$ representations is a conjecture of Treumann and Venkatesh [Reference Treumann and VenkateshTV16, Conjecture 6.6], which predicts that Tate cohomology should realize functoriality in the local Langlands correspondence for mod
$\ell$ representations is a conjecture of Treumann and Venkatesh [Reference Treumann and VenkateshTV16, Conjecture 6.6], which predicts that Tate cohomology should realize functoriality in the local Langlands correspondence for mod ![]() $\ell$ representations. This was proved in [Reference FengFen24, Theorem 1.2] for the Genestier–Lafforgue correspondence, thanks to which our task amounts to computing the Tate cohomology of toral supercuspidal representations. However, Tate cohomology is tricky to calculate in general; for a general supercuspidal representation presented via a Yu datum, as considered in [Reference KalethaKal19], it would be a challenge even to determine whether the Tate cohomology is non-zero. Crucial traction for this problem is provided by recent work of Chan and Ivanov [Reference Chan and IvanovCI21] and of Chan and Oi [Reference Chan and OiCO23] on geometric models for toral supercuspidal representations in terms of ‘deep level Deligne–Lusztig induction’; we ultimately compute the Tate cohomology by applying equivariant localization tools to their deep level Deligne–Lusztig varieties.
$\ell$ representations. This was proved in [Reference FengFen24, Theorem 1.2] for the Genestier–Lafforgue correspondence, thanks to which our task amounts to computing the Tate cohomology of toral supercuspidal representations. However, Tate cohomology is tricky to calculate in general; for a general supercuspidal representation presented via a Yu datum, as considered in [Reference KalethaKal19], it would be a challenge even to determine whether the Tate cohomology is non-zero. Crucial traction for this problem is provided by recent work of Chan and Ivanov [Reference Chan and IvanovCI21] and of Chan and Oi [Reference Chan and OiCO23] on geometric models for toral supercuspidal representations in terms of ‘deep level Deligne–Lusztig induction’; we ultimately compute the Tate cohomology by applying equivariant localization tools to their deep level Deligne–Lusztig varieties.
2. Notation and terminology
We fix a finite field ![]() ${\mathbb {F}}_q$ of characteristic
${\mathbb {F}}_q$ of characteristic ![]() $p$. Let
$p$. Let ![]() $X$ be a smooth, geometrically connected, and projective curve over
$X$ be a smooth, geometrically connected, and projective curve over ![]() ${\mathbb {F}}_q$ and
${\mathbb {F}}_q$ and ![]() $K = \mathbb {F}_q(X)$, and let
$K = \mathbb {F}_q(X)$, and let ![]() $G$ be a split reductive group over
$G$ be a split reductive group over ![]() $K$. The notation
$K$. The notation ![]() $\ell$ always denotes a prime not equal to
$\ell$ always denotes a prime not equal to ![]() $p$.
$p$.
2.1 Notation related to global and local fields
We write ![]() $K^{\rm s}$ for a fixed choice of separable closure and
$K^{\rm s}$ for a fixed choice of separable closure and ![]() $\Gamma _K := \operatorname {Gal}(K^{\rm s} / K)$ for the corresponding Galois group. For
$\Gamma _K := \operatorname {Gal}(K^{\rm s} / K)$ for the corresponding Galois group. For ![]() $S$ a finite set of places of
$S$ a finite set of places of ![]() $K$, we write
$K$, we write ![]() $K_S$ for the maximal subextension of
$K_S$ for the maximal subextension of ![]() $K^{\rm s}$ unramified outside
$K^{\rm s}$ unramified outside ![]() $S$, and
$S$, and ![]() $\Gamma _{K, S} := \operatorname {Gal}(K_S / K)$. If
$\Gamma _{K, S} := \operatorname {Gal}(K_S / K)$. If ![]() $v$ is a place of
$v$ is a place of ![]() $K$, then
$K$, then ![]() $\Gamma _{K_v} = \operatorname {Gal}(K_v^{\rm s} / K_v)$ will denote the decomposition group, and
$\Gamma _{K_v} = \operatorname {Gal}(K_v^{\rm s} / K_v)$ will denote the decomposition group, and ![]() $\Gamma _{K_v} \to \Gamma _K$ the homomorphism corresponding to a fixed choice of
$\Gamma _{K_v} \to \Gamma _K$ the homomorphism corresponding to a fixed choice of ![]() $K$-embedding
$K$-embedding ![]() $K^{\rm s} \hookrightarrow K_v^{\rm s}$. If
$K^{\rm s} \hookrightarrow K_v^{\rm s}$. If ![]() $v \not \in S$, then
$v \not \in S$, then ![]() $\operatorname {Frob}_v \in \Gamma _{K, S}$ denotes a choice of geometric Frobenius element at the place
$\operatorname {Frob}_v \in \Gamma _{K, S}$ denotes a choice of geometric Frobenius element at the place ![]() $v$. We will identify the set of places of
$v$. We will identify the set of places of ![]() $K$ with the set of closed points of
$K$ with the set of closed points of ![]() $X$. For a place
$X$. For a place ![]() $v \in |X|$ we write
$v \in |X|$ we write ![]() $q_v = \# k(v) = \# ({\mathcal {O}}_{K_v} / \varpi _v {\mathcal {O}}_{K_v})$ for the size of the residue field at
$q_v = \# k(v) = \# ({\mathcal {O}}_{K_v} / \varpi _v {\mathcal {O}}_{K_v})$ for the size of the residue field at ![]() $v$. We write
$v$. We write ![]() $| \cdot |_v$ for the norm on
$| \cdot |_v$ for the norm on ![]() $K_v$, normalized so that
$K_v$, normalized so that ![]() $|\varpi _v|_v = q_v^{-1}$; then the product formula holds. We write
$|\varpi _v|_v = q_v^{-1}$; then the product formula holds. We write ![]() $\widehat {{\mathcal {O}}}_{K} = \prod _{v \in X} {\mathcal {O}}_{K_v}$. We will write
$\widehat {{\mathcal {O}}}_{K} = \prod _{v \in X} {\mathcal {O}}_{K_v}$. We will write ![]() $W_{K_v}$ for the Weil group of the local field
$W_{K_v}$ for the Weil group of the local field ![]() $K_v$.
$K_v$.
2.2 Notation related to group schemes
If ![]() $G, H, \ldots$ are group schemes over a base
$G, H, \ldots$ are group schemes over a base ![]() $S$, then we use Gothic letters
$S$, then we use Gothic letters ![]() ${\mathfrak g}, {\mathfrak h}, \ldots$ to denote their Lie algebras, and
${\mathfrak g}, {\mathfrak h}, \ldots$ to denote their Lie algebras, and ![]() $G_T, {\mathfrak g}_T, \ldots$ to denote the base changes of these objects relative to a scheme
$G_T, {\mathfrak g}_T, \ldots$ to denote the base changes of these objects relative to a scheme ![]() $T \to S$. If
$T \to S$. If ![]() $G$ acts on an
$G$ acts on an ![]() $S$-scheme
$S$-scheme ![]() $X$ and
$X$ and ![]() $x \in X(T)$, then we write
$x \in X(T)$, then we write ![]() $Z_G(x)$ or
$Z_G(x)$ or ![]() $Z_{G_T}(x)$ for the scheme-theoretic stabilizer of
$Z_{G_T}(x)$ for the scheme-theoretic stabilizer of ![]() $x$; it is a group scheme over
$x$; it is a group scheme over ![]() $T$. We denote the center of
$T$. We denote the center of ![]() $G$ by
$G$ by ![]() $Z_G$. We say that a group scheme
$Z_G$. We say that a group scheme ![]() $G$ over
$G$ over ![]() $S$ is reductive if
$S$ is reductive if ![]() $G$ is smooth and affine with reductive (and therefore connected) geometric fibres.
$G$ is smooth and affine with reductive (and therefore connected) geometric fibres.
2.3 Notation related to coefficient rings
When doing deformation theory, we will generally fix a prime ![]() $\ell$ and an algebraic closure
$\ell$ and an algebraic closure ![]() $\overline {{\mathbb {Q}}}_\ell$ of
$\overline {{\mathbb {Q}}}_\ell$ of ![]() ${\mathbb {Q}}_\ell$. A finite extension
${\mathbb {Q}}_\ell$. A finite extension ![]() $E / {\mathbb {Q}}_\ell$ inside
$E / {\mathbb {Q}}_\ell$ inside ![]() $\overline {{\mathbb {Q}}}_\ell$ will be called a coefficient field; when such a field
$\overline {{\mathbb {Q}}}_\ell$ will be called a coefficient field; when such a field ![]() $E$ has been fixed, we will write
$E$ has been fixed, we will write ![]() ${\mathcal {O}}$ or
${\mathcal {O}}$ or ![]() ${\mathcal {O}}_E$ for its ring of integers,
${\mathcal {O}}_E$ for its ring of integers, ![]() $k$ or
$k$ or ![]() $k_E$ for its residue field, and
$k_E$ for its residue field, and ![]() $\varpi$ or
$\varpi$ or ![]() $\varpi _E$ for a choice of uniformizer of
$\varpi _E$ for a choice of uniformizer of ![]() ${\mathcal {O}}_E$. We write
${\mathcal {O}}_E$. We write ![]() ${\mathcal {C}}_{\mathcal {O}}$ for the category of Artinian local
${\mathcal {C}}_{\mathcal {O}}$ for the category of Artinian local ![]() ${\mathcal {O}}$-algebras with residue field
${\mathcal {O}}$-algebras with residue field ![]() $k$; if
$k$; if ![]() $A \in {\mathcal {C}}_{\mathcal {O}}$, then we write
$A \in {\mathcal {C}}_{\mathcal {O}}$, then we write ![]() ${\mathfrak m}_A$ for its maximal ideal. Then
${\mathfrak m}_A$ for its maximal ideal. Then ![]() $A$ comes with the data of an isomorphism
$A$ comes with the data of an isomorphism ![]() $k \cong A / {\mathfrak m}_A$.
$k \cong A / {\mathfrak m}_A$.
2.4 Dual groups
In this paper, we will view the dual group ![]() $\widehat {G}$ of
$\widehat {G}$ of ![]() $G$ as a split reductive group over
$G$ as a split reductive group over ![]() $\mathbb {Z}$. Our definition of
$\mathbb {Z}$. Our definition of ![]() $\widehat {G}$ follows [Reference Böckle, Harris, Khare and ThorneBHKT19, § 2.1]. A prime
$\widehat {G}$ follows [Reference Böckle, Harris, Khare and ThorneBHKT19, § 2.1]. A prime ![]() $\ell$ is called a very good characteristic for
$\ell$ is called a very good characteristic for ![]() ${\widehat {G}}$ if it satisfies the conditions in the table below for all the simple factors of
${\widehat {G}}$ if it satisfies the conditions in the table below for all the simple factors of ![]() $\widehat {G}$ (referring to the absolute root system types):
$\widehat {G}$ (referring to the absolute root system types):

3. Deformation problems
In this section we set up the results on Galois deformation theory that will be used later for automorphy lifting.
3.1 Setup for the general theory
Let ![]() ${\widehat {G}}$ be a split semisimple group over
${\widehat {G}}$ be a split semisimple group over ![]() ${\mathbb {Z}}$. We fix a prime
${\mathbb {Z}}$. We fix a prime ![]() $\ell$ which is a very good characteristic for
$\ell$ which is a very good characteristic for ![]() ${\widehat {G}}$, as well as a coefficient field
${\widehat {G}}$, as well as a coefficient field ![]() $E \subset \overline {{\mathbb {Q}}}_\ell$. We also fix an absolutely irreducible representation
$E \subset \overline {{\mathbb {Q}}}_\ell$. We also fix an absolutely irreducible representation ![]() $\overline {\sigma }$ of
$\overline {\sigma }$ of ![]() $\Gamma _{K,S}$. We recall the results of [Reference Böckle, Harris, Khare and ThorneBHKT19] on the deformation theory of representations of
$\Gamma _{K,S}$. We recall the results of [Reference Böckle, Harris, Khare and ThorneBHKT19] on the deformation theory of representations of ![]() $\Gamma _{K,S}$ to
$\Gamma _{K,S}$ to ![]() ${\widehat {G}}$ with
${\widehat {G}}$ with ![]() $\ell$-adic coefficients.
$\ell$-adic coefficients.
Lemma 3.1 [Reference Böckle, Harris, Khare and ThorneBHKT19, Lemma 5.1]
Let ![]() ${\overline {\sigma }}: \Gamma _{K,S} \rightarrow {\widehat {G}}(k)$ be an absolutely
${\overline {\sigma }}: \Gamma _{K,S} \rightarrow {\widehat {G}}(k)$ be an absolutely ![]() ${\widehat {G}}$-irreducible homomorphism. The scheme-theoretic centralizer of
${\widehat {G}}$-irreducible homomorphism. The scheme-theoretic centralizer of ![]() ${\overline {\sigma }}(\Gamma _{K,S})$ in
${\overline {\sigma }}(\Gamma _{K,S})$ in ![]() ${\widehat {G}}_k^{{\rm ad}}$ is étale over
${\widehat {G}}_k^{{\rm ad}}$ is étale over ![]() $k$, and
$k$, and ![]() $H^0(\Gamma _{K,S}, {\rm ad} \,{\overline {\sigma }}) = 0$.
$H^0(\Gamma _{K,S}, {\rm ad} \,{\overline {\sigma }}) = 0$.
Let ![]() $A \in {\mathcal {C}}_{\mathcal {O}}$. We define liftings and deformations of
$A \in {\mathcal {C}}_{\mathcal {O}}$. We define liftings and deformations of ![]() ${\overline {\sigma }}$ over
${\overline {\sigma }}$ over ![]() $A$ as in [Reference Böckle, Harris, Khare and ThorneBHKT19, § 5.1], and let
$A$ as in [Reference Böckle, Harris, Khare and ThorneBHKT19, § 5.1], and let ![]() $\operatorname {Def}_{{\overline {\sigma }}} : {\mathcal {C}}_{\mathcal {O}} \to \operatorname {Sets}$ be the functor that associates to
$\operatorname {Def}_{{\overline {\sigma }}} : {\mathcal {C}}_{\mathcal {O}} \to \operatorname {Sets}$ be the functor that associates to ![]() $A \in {\mathcal {C}}_{\mathcal {O}}$ the set of deformations of
$A \in {\mathcal {C}}_{\mathcal {O}}$ the set of deformations of ![]() ${\overline {\sigma }}$ over
${\overline {\sigma }}$ over ![]() $A$. Then we have the following proposition.
$A$. Then we have the following proposition.
Proposition 3.2 [Reference Böckle, Harris, Khare and ThorneBHKT19, Propositions 5.10]
The functor ![]() $\operatorname {Def}_{{\overline {\sigma }}}$ is pro-represented by a complete Noetherian local
$\operatorname {Def}_{{\overline {\sigma }}}$ is pro-represented by a complete Noetherian local ![]() ${\mathcal {O}}$-algebra
${\mathcal {O}}$-algebra ![]() $R_{{\overline {\sigma }}} = R_{{\overline {\sigma }},S}$. (We will include the subscript
$R_{{\overline {\sigma }}} = R_{{\overline {\sigma }},S}$. (We will include the subscript ![]() $S$ in the notation when we want to let
$S$ in the notation when we want to let ![]() $S$ vary.)
$S$ vary.)
3.2 Local deformation conditions
So far we have considered deformations of ![]() ${\overline {\sigma }}$ with no restriction on the points in
${\overline {\sigma }}$ with no restriction on the points in ![]() $S$. We now introduce local deformation conditions, following the discussion in [Reference Clozel, Harris and TaylorCHT08, § 2.2], and for general groups in [Reference PatrikisPat16, § 3.2], with notation as in [Reference Khare and ThorneKT17, § 4]. For each
$S$. We now introduce local deformation conditions, following the discussion in [Reference Clozel, Harris and TaylorCHT08, § 2.2], and for general groups in [Reference PatrikisPat16, § 3.2], with notation as in [Reference Khare and ThorneKT17, § 4]. For each ![]() $v \in S$ let
$v \in S$ let ![]() ${\Gamma _{K_v}} \subset \Gamma _{K,S}$ be a decomposition group at
${\Gamma _{K_v}} \subset \Gamma _{K,S}$ be a decomposition group at ![]() $v$, and let
$v$, and let ![]() ${\overline {\sigma }}_v$ denote the restriction of
${\overline {\sigma }}_v$ denote the restriction of ![]() ${\overline {\sigma }}$ to
${\overline {\sigma }}$ to ![]() ${\Gamma _{K_v}}$. Let
${\Gamma _{K_v}}$. Let ![]() ${\mathcal {D}}^\square _{{\overline {\sigma }},v}$ denote the functor on
${\mathcal {D}}^\square _{{\overline {\sigma }},v}$ denote the functor on ![]() ${\mathcal {C}}_{\mathcal {O}}$ which to
${\mathcal {C}}_{\mathcal {O}}$ which to ![]() $A \in \mathcal{C}_{\mathcal{O}}$ associates the set of liftings of
$A \in \mathcal{C}_{\mathcal{O}}$ associates the set of liftings of ![]() ${\overline{\sigma}}$ to A; then
${\overline{\sigma}}$ to A; then ![]() ${\mathcal {D}}^\square _{{\overline {\sigma }},v}$ is represented by a ring
${\mathcal {D}}^\square _{{\overline {\sigma }},v}$ is represented by a ring ![]() $R^\square _{{\overline {\sigma }},v}$. As in [Reference Khare and ThorneKT17, Definition 4.1], we define a local deformation problem for
$R^\square _{{\overline {\sigma }},v}$. As in [Reference Khare and ThorneKT17, Definition 4.1], we define a local deformation problem for ![]() ${\overline {\sigma }}_v$ to be a subfunctor
${\overline {\sigma }}_v$ to be a subfunctor ![]() ${\mathcal {D}}_v \subset {\mathcal {D}}^\square _{{\overline {\sigma }},v}$ such that:
${\mathcal {D}}_v \subset {\mathcal {D}}^\square _{{\overline {\sigma }},v}$ such that:
•
 ${\mathcal {D}}_v$ is represented by a quotient of
${\mathcal {D}}_v$ is represented by a quotient of  $R^\square _{{\overline {\sigma }},v}$; and
$R^\square _{{\overline {\sigma }},v}$; and• for any
 $A \in {\mathcal {O}}$, if
$A \in {\mathcal {O}}$, if  $\sigma \in {\mathcal {D}}_v(A)$ and
$\sigma \in {\mathcal {D}}_v(A)$ and  $\alpha \in \ker [{\widehat {G}}(A) \rightarrow {\widehat {G}}(k)]$ then
$\alpha \in \ker [{\widehat {G}}(A) \rightarrow {\widehat {G}}(k)]$ then  ${\rm ad}(\alpha )(\sigma ) \in {\mathcal {D}}_v(A)$.
${\rm ad}(\alpha )(\sigma ) \in {\mathcal {D}}_v(A)$.
Definition 3.3 A global deformation problem for ![]() ${\overline {\sigma }}$ is a collection
${\overline {\sigma }}$ is a collection ![]() ${\mathcal {D}} := (S, \{{\mathcal {D}}_v\}_{v \in S})$ where for each
${\mathcal {D}} := (S, \{{\mathcal {D}}_v\}_{v \in S})$ where for each ![]() $v \in S$,
$v \in S$, ![]() ${\mathcal {D}}_v$ is a local deformation problem for
${\mathcal {D}}_v$ is a local deformation problem for ![]() ${\overline {\sigma }}_v$.
${\overline {\sigma }}_v$.
For ![]() $A \in {\mathcal {C}}_{\mathcal {O}}$, a deformation
$A \in {\mathcal {C}}_{\mathcal {O}}$, a deformation ![]() $\sigma : \Gamma _{K,S} \rightarrow {\widehat {G}}(A)$ is of type
$\sigma : \Gamma _{K,S} \rightarrow {\widehat {G}}(A)$ is of type ![]() ${\mathcal {D}}$ if for every
${\mathcal {D}}$ if for every ![]() $v \in S$, the restriction of
$v \in S$, the restriction of ![]() $\sigma$ to
$\sigma$ to ![]() ${\Gamma _{K_v}}$ belongs to
${\Gamma _{K_v}}$ belongs to ![]() ${\mathcal {D}}_v$.
${\mathcal {D}}_v$.
The functor of deformations of ![]() ${\overline {\sigma }}$ of type
${\overline {\sigma }}$ of type ![]() ${\mathcal {D}}$ is denoted
${\mathcal {D}}$ is denoted ![]() $\operatorname {Def}_{{\overline {\sigma }},{\mathcal {D}}} = \operatorname {Def}_{{\overline {\sigma }},S,{\mathcal {D}}}$. Again, we will emphasize the subscript
$\operatorname {Def}_{{\overline {\sigma }},{\mathcal {D}}} = \operatorname {Def}_{{\overline {\sigma }},S,{\mathcal {D}}}$. Again, we will emphasize the subscript ![]() $S$ when we want to contemplate varying
$S$ when we want to contemplate varying ![]() $S$.
$S$.
To each local deformation problem ![]() ${\mathcal {D}}_v$ we attach a
${\mathcal {D}}_v$ we attach a ![]() $k$-subspace
$k$-subspace ![]() $L_v \subset H^1(G_{K_v}, {\rm ad}({\overline {\sigma }}))$ as in [Reference PatrikisPat16, § 3.2].
$L_v \subset H^1(G_{K_v}, {\rm ad}({\overline {\sigma }}))$ as in [Reference PatrikisPat16, § 3.2].
Definition 3.4 The deformation problem ![]() ${\mathcal {D}}_v$ is balanced if
${\mathcal {D}}_v$ is balanced if ![]() $\dim L_v = \dim H^0(G_{K_v}, {\rm ad}({\overline {\sigma }}))$.
$\dim L_v = \dim H^0(G_{K_v}, {\rm ad}({\overline {\sigma }}))$.
Example The minimal deformation problems considered in [Reference Clozel, Harris and TaylorCHT08, § 2.4.4] are balanced.
Example 3.5 The deformation problem ![]() ${\mathcal {D}}_v$ is unrestricted if
${\mathcal {D}}_v$ is unrestricted if ![]() ${\mathcal {D}}_v = {\mathcal {D}}^\square _{{\overline {\sigma }},v}$. In this case we have
${\mathcal {D}}_v = {\mathcal {D}}^\square _{{\overline {\sigma }},v}$. In this case we have ![]() $L_v = H^1({\Gamma _{K_v}}, {\rm ad}({\overline {\sigma }}))$.
$L_v = H^1({\Gamma _{K_v}}, {\rm ad}({\overline {\sigma }}))$.
Recall that for all ![]() $v \in S$, Tate's local Euler characteristic formula for any
$v \in S$, Tate's local Euler characteristic formula for any ![]() $k[{\Gamma _{K_v}}]$-module
$k[{\Gamma _{K_v}}]$-module ![]() $M$ reduces to
$M$ reduces to
because ![]() $\ell \neq p$. Hence, if
$\ell \neq p$. Hence, if ![]() $H^2({\Gamma _{K_v}}, {\rm ad}({\overline {\sigma }})) = 0$ then the unrestricted deformation problem
$H^2({\Gamma _{K_v}}, {\rm ad}({\overline {\sigma }})) = 0$ then the unrestricted deformation problem ![]() ${\mathcal {D}}_v$ is balanced.
${\mathcal {D}}_v$ is balanced.
Note that local duality implies that
3.3 Selmer groups
Given a global deformation problem ![]() ${\mathcal {D}}$, we define
${\mathcal {D}}$, we define
 \begin{equation} H^1_{{\mathcal{D}}}(\Gamma_{K,S},{\rm ad}({\overline{\sigma}})) := \ker \bigg[H^1(\Gamma_{K,S},{\rm ad}({\overline{\sigma}})) \rightarrow \bigoplus_{v \in S} H^1({\Gamma_{K_v}}, {\rm ad}({\overline{\sigma}}))/L_v \bigg], \end{equation}
\begin{equation} H^1_{{\mathcal{D}}}(\Gamma_{K,S},{\rm ad}({\overline{\sigma}})) := \ker \bigg[H^1(\Gamma_{K,S},{\rm ad}({\overline{\sigma}})) \rightarrow \bigoplus_{v \in S} H^1({\Gamma_{K_v}}, {\rm ad}({\overline{\sigma}}))/L_v \bigg], \end{equation}
and let ![]() $h^1_{{\mathcal {D}}}(\Gamma _{K,S},{\rm ad}({\overline {\sigma }}) ) := \dim _k H^1_{{\mathcal {D}}}(\Gamma _{K,S},{\rm ad}({\overline {\sigma }}))$.
$h^1_{{\mathcal {D}}}(\Gamma _{K,S},{\rm ad}({\overline {\sigma }}) ) := \dim _k H^1_{{\mathcal {D}}}(\Gamma _{K,S},{\rm ad}({\overline {\sigma }}))$.
With ![]() $L_v$ as above, let
$L_v$ as above, let ![]() $L_v^\perp \subset H^1({\Gamma _{K_v}}, {\rm ad}({\overline {\sigma }})^{\vee }(1))$ denote its orthogonal complement under the local duality pairing. We define
$L_v^\perp \subset H^1({\Gamma _{K_v}}, {\rm ad}({\overline {\sigma }})^{\vee }(1))$ denote its orthogonal complement under the local duality pairing. We define
 \[ H^1_{{\mathcal{D}}^{\perp}}(\Gamma_{K,S},{\rm ad}({\overline{\sigma}})^{\vee}(1)) := \ker \bigg[H^1(\Gamma_{K,S},{\rm ad}({\overline{\sigma}})^{\vee}(1)) \rightarrow \bigoplus_{v \in S} H^1({\Gamma_{K_v}}, {\rm ad}({\overline{\sigma}})^{\vee}(1))/L_v^{\perp} \bigg], \]
\[ H^1_{{\mathcal{D}}^{\perp}}(\Gamma_{K,S},{\rm ad}({\overline{\sigma}})^{\vee}(1)) := \ker \bigg[H^1(\Gamma_{K,S},{\rm ad}({\overline{\sigma}})^{\vee}(1)) \rightarrow \bigoplus_{v \in S} H^1({\Gamma_{K_v}}, {\rm ad}({\overline{\sigma}})^{\vee}(1))/L_v^{\perp} \bigg], \]
and let ![]() $h^1_{{\mathcal {D}}^{\perp }}(\Gamma _{K,S},{\rm ad}({\overline {\sigma }})^{\vee } (1)) := \dim _k H^1_{{\mathcal {D}}^{\perp }}(\Gamma _{K,S},{\rm ad}({\overline {\sigma }})^{\vee }(1))$.
$h^1_{{\mathcal {D}}^{\perp }}(\Gamma _{K,S},{\rm ad}({\overline {\sigma }})^{\vee } (1)) := \dim _k H^1_{{\mathcal {D}}^{\perp }}(\Gamma _{K,S},{\rm ad}({\overline {\sigma }})^{\vee }(1))$.
Proposition 3.6
(i) The functor
 $\operatorname {Def}_{{\overline {\sigma }},{\mathcal {D}}}$ is pro-represented by a complete Noetherian local
$\operatorname {Def}_{{\overline {\sigma }},{\mathcal {D}}}$ is pro-represented by a complete Noetherian local  ${\mathcal {O}}$-algebra
${\mathcal {O}}$-algebra  $R_{{\overline {\sigma }},{\mathcal {D}}} = R_{{\overline {\sigma }},S,{\mathcal {D}}}$.
$R_{{\overline {\sigma }},{\mathcal {D}}} = R_{{\overline {\sigma }},S,{\mathcal {D}}}$.(ii) There is a surjection
 ${\mathcal {O}} \unicode{x27E6} X_1, \ldots X_g \unicode{x27E7} \twoheadrightarrow R_{{\overline {\sigma }}, S, {\mathcal {D}} }$, where
${\mathcal {O}} \unicode{x27E6} X_1, \ldots X_g \unicode{x27E7} \twoheadrightarrow R_{{\overline {\sigma }}, S, {\mathcal {D}} }$, where  $g = \dim _k H^1_{{\mathcal {D}}}(\Gamma _{K, S}, {\rm ad}\, {\overline {\sigma }})$.
$g = \dim _k H^1_{{\mathcal {D}}}(\Gamma _{K, S}, {\rm ad}\, {\overline {\sigma }})$.
Proof. For (i) the proof is the same as for [Reference Clozel, Harris and TaylorCHT08, Proposition 2.2.9], and for (ii) the proof is the same as for [Reference Clozel, Harris and TaylorCHT08, Corollary 2.2.12].
3.4 Abundant subgroups
We recall two definitions from [Reference Böckle, Harris, Khare and ThorneBHKT19].
Definition 3.7 Let ![]() $\Gamma$ be an abstract group, and let
$\Gamma$ be an abstract group, and let ![]() ${\widehat {G}}$ be a reductive group over
${\widehat {G}}$ be a reductive group over ![]() $k$.
$k$.
(i) A homomorphism
 $\sigma : \Gamma \to {\widehat {G}}(k)$ is said to be absolutely
$\sigma : \Gamma \to {\widehat {G}}(k)$ is said to be absolutely  ${\widehat {G}}$-completely reducible (respectively, absolutely
${\widehat {G}}$-completely reducible (respectively, absolutely  ${\widehat {G}}$-irreducible) if it is
${\widehat {G}}$-irreducible) if it is  ${\widehat {G}}$-completely reducible (respectively,
${\widehat {G}}$-completely reducible (respectively,  ${\widehat {G}}$-irreducible) after extension of scalars to an algebraic closure of
${\widehat {G}}$-irreducible) after extension of scalars to an algebraic closure of  $k$.
$k$.
Suppose now that ![]() ${\widehat {G}}$ is semisimple, and let
${\widehat {G}}$ is semisimple, and let ![]() $\overline k$ be an algebraic closure of
$\overline k$ be an algebraic closure of ![]() $k$.
$k$.
(iii) A finite subgroup
 $H \subset {\widehat {G}}(\overline k)$ is said to be
$H \subset {\widehat {G}}(\overline k)$ is said to be  ${\widehat {G}}$-abundant over
${\widehat {G}}$-abundant over  $k$ if it satisfies the following conditions:
$k$ if it satisfies the following conditions:
(a) The group
 $H$ is contained in
$H$ is contained in  ${\widehat {G}}(k)$.
${\widehat {G}}(k)$.(b) The groups
 $H^0(H, \widehat {{\mathfrak g}}_{k})$,
$H^0(H, \widehat {{\mathfrak g}}_{k})$,  $H^0(H, \widehat {{\mathfrak g}}^\vee _{k})$,
$H^0(H, \widehat {{\mathfrak g}}^\vee _{k})$,  $H^1(H, \widehat {{\mathfrak g}}^\vee _{k})$, and
$H^1(H, \widehat {{\mathfrak g}}^\vee _{k})$, and  $H^1(H, k)$ all vanish.
$H^1(H, k)$ all vanish.(c) For each regular semisimple element
 $h \in H$, the torus
$h \in H$, the torus  $Z_{{\widehat {G}}}(h)^\circ \subset {\widehat {G}}$ is split over
$Z_{{\widehat {G}}}(h)^\circ \subset {\widehat {G}}$ is split over  $k$.
$k$.(d) For every simple
 $k[H]$-submodule
$k[H]$-submodule  $W \subset \widehat {{\mathfrak g}}^\vee$, there exists a regular semisimple element
$W \subset \widehat {{\mathfrak g}}^\vee$, there exists a regular semisimple element  $h \in H$ such that
$h \in H$ such that  $W^h \neq 0$ and
$W^h \neq 0$ and  $Z_{{\widehat {G}}}(h)$ is connected. (We recall that
$Z_{{\widehat {G}}}(h)$ is connected. (We recall that  $Z_{{\widehat {G}}}(h)$ is always connected if
$Z_{{\widehat {G}}}(h)$ is always connected if  ${\widehat {G}}$ is simply connected.)
${\widehat {G}}$ is simply connected.)
Lemma 3.8 Suppose ![]() ${\widehat {G}}$ is simple and split over
${\widehat {G}}$ is simple and split over ![]() $k$. Let
$k$. Let ![]() ${\widehat {G}}^{\rm sc}$ denote the simply connected cover of
${\widehat {G}}^{\rm sc}$ denote the simply connected cover of ![]() ${\widehat {G}}$, and let
${\widehat {G}}$, and let ![]() ${\widehat {G}}(k)^+$ denote the image of
${\widehat {G}}(k)^+$ denote the image of ![]() ${\widehat {G}}^{\rm sc}(k)$ in
${\widehat {G}}^{\rm sc}(k)$ in ![]() ${\widehat {G}}(k)$. Let
${\widehat {G}}(k)$. Let ![]() $H$ be a group with
$H$ be a group with ![]() ${\widehat {G}}^+(k)\subset H\subset {\widehat {G}}(k)$ and suppose that (
${\widehat {G}}^+(k)\subset H\subset {\widehat {G}}(k)$ and suppose that (![]() $k$, type of
$k$, type of ![]() ${\widehat {G}}$) is not in the following list:
${\widehat {G}}$) is not in the following list:
Then there exists a finite field ![]() $k_1\supset k$ such that for all finite fields
$k_1\supset k$ such that for all finite fields ![]() $k'\supset k_1$ the group
$k'\supset k_1$ the group ![]() $H$ is
$H$ is ![]() ${\widehat {G}}$-abundant over
${\widehat {G}}$-abundant over ![]() $k'$.
$k'$.
Proof. We will prove the following claims for ![]() $(k,\mathrm {type\, of\, }{\widehat {G}})$ not in the above list:
$(k,\mathrm {type\, of\, }{\widehat {G}})$ not in the above list:
(i) The adjoint module
 $\widehat {{\mathfrak g}}_{k}$ is self-dual as a
$\widehat {{\mathfrak g}}_{k}$ is self-dual as a  $k[H]$-representation,
$k[H]$-representation,(ii) The groups
 $H^0(H, \widehat {{\mathfrak g}}_{k})$,
$H^0(H, \widehat {{\mathfrak g}}_{k})$,  $H^1(H, \widehat {{\mathfrak g}}_{k})$, and
$H^1(H, \widehat {{\mathfrak g}}_{k})$, and  $H^1(H, k)$ all vanish.
$H^1(H, k)$ all vanish.(iii) The action of
 $H$ on
$H$ on  $\widehat {{\mathfrak g}}_{k}$ is absolutely irreducible.
$\widehat {{\mathfrak g}}_{k}$ is absolutely irreducible.(iv) The group
 $H$ contains strongly regular semisimple elements
$H$ contains strongly regular semisimple elements  $h$, i.e.
$h$, i.e.  $h$ such that
$h$ such that  $Z_{{\widehat {G}}}(h)$ is connected.
$Z_{{\widehat {G}}}(h)$ is connected.
Let us first show that the claims suffice to prove the lemma. Indeed, condition (a) is obvious, condition (b) is the same as (ii) (given (i)), while condition (c) is automatic if ![]() $k_1$ is chosen to split all of the finitely many
$k_1$ is chosen to split all of the finitely many ![]() $k$-rational tori
$k$-rational tori ![]() $Z_{{\widehat {G}}}(h)^\circ$ in
$Z_{{\widehat {G}}}(h)^\circ$ in ![]() ${\widehat {G}}$. Finally, given (iii), condition (d) comes down to the existence of strongly regular semisimple
${\widehat {G}}$. Finally, given (iii), condition (d) comes down to the existence of strongly regular semisimple ![]() $h$, as in (iv), because
$h$, as in (iv), because ![]() $(\widehat {{\mathfrak g}}^\vee )^h$ always contains the Lie algebra of the centralizer of
$(\widehat {{\mathfrak g}}^\vee )^h$ always contains the Lie algebra of the centralizer of ![]() $h$.
$h$.
It remains to establish the claim. Parts (i) to (iii) with many details can be found in [Reference Arias-de Reyna and BöckleAB, § 3], which, however, largely builds on further references, which we now briefly recall. We first observe that ![]() $\widehat {{\mathfrak g}}_{k}$ is an absolutely irreducible
$\widehat {{\mathfrak g}}_{k}$ is an absolutely irreducible ![]() $k[H]$-representation, essentially by results of Hiss [Reference HissHis84] and Hogeweij [Reference HogeweijHog82]; see [Reference Arias-de Reyna and BöckleAB, Proposition 3.22]. Now because
$k[H]$-representation, essentially by results of Hiss [Reference HissHis84] and Hogeweij [Reference HogeweijHog82]; see [Reference Arias-de Reyna and BöckleAB, Proposition 3.22]. Now because ![]() $\widehat {{\mathfrak g}}_{k}$ is absolutely irreducible, to prove self-duality it suffices to see that
$\widehat {{\mathfrak g}}_{k}$ is absolutely irreducible, to prove self-duality it suffices to see that ![]() $\widehat {{\mathfrak g}}_{k}$ and
$\widehat {{\mathfrak g}}_{k}$ and ![]() $\widehat {{\mathfrak g}}_{k}^\vee$ have the same weights. But this is clear since with any root
$\widehat {{\mathfrak g}}_{k}^\vee$ have the same weights. But this is clear since with any root ![]() $\alpha$ of the Lie algebra
$\alpha$ of the Lie algebra ![]() $\widehat {{\mathfrak g}}_{k}$,
$\widehat {{\mathfrak g}}_{k}$, ![]() $-\alpha$ is also a root, and both have multiplicity
$-\alpha$ is also a root, and both have multiplicity ![]() $1$. This settles (i) and (iii), and the first assertion of (ii).
$1$. This settles (i) and (iii), and the first assertion of (ii).
Next, a largely classical result, completed by Tits, asserts that ![]() ${\widehat {G}}(k)^+$ is perfect, unless
${\widehat {G}}(k)^+$ is perfect, unless ![]() $(k,\mathrm {type\, of\, }{\widehat {G}})$ is
$(k,\mathrm {type\, of\, }{\widehat {G}})$ is ![]() $(\mathbb {F}_3,A_1)$; see [Reference Malle and TestermanMT11, Thm. 24.17]. Because
$(\mathbb {F}_3,A_1)$; see [Reference Malle and TestermanMT11, Thm. 24.17]. Because ![]() ${\widehat {G}}$ is split and
${\widehat {G}}$ is split and ![]() $l$ is of very good characteristic for
$l$ is of very good characteristic for ![]() ${\widehat {G}}$, there is only a single exception. The latter also implies that
${\widehat {G}}$, there is only a single exception. The latter also implies that ![]() ${\widehat {G}}(k)/{\widehat {G}}(k)^+$ is of order prime to the characteristic
${\widehat {G}}(k)/{\widehat {G}}(k)^+$ is of order prime to the characteristic ![]() $l$ of
$l$ of ![]() $k$. Hence
$k$. Hence ![]() $H^1(H, k)=\operatorname {Hom}(H, k)$ vanishes, and this shows the third part of (ii); see [Reference Arias-de Reyna and BöckleAB, Corollary 3.12].
$H^1(H, k)=\operatorname {Hom}(H, k)$ vanishes, and this shows the third part of (ii); see [Reference Arias-de Reyna and BöckleAB, Corollary 3.12].
We now turn to the remaining condition ![]() $H^1({\widehat {G}}(k), \widehat {{\mathfrak g}}_{k}) = 0$ from (ii). The most complete vanishing results for
$H^1({\widehat {G}}(k), \widehat {{\mathfrak g}}_{k}) = 0$ from (ii). The most complete vanishing results for ![]() $H^1(H, \widehat {{\mathfrak g}}_{k})$ are due to Völklein with earlier work by Cline, Parshall, Scott in the A-D-E cases and by Hertzig (unpublished). We observe that
$H^1(H, \widehat {{\mathfrak g}}_{k})$ are due to Völklein with earlier work by Cline, Parshall, Scott in the A-D-E cases and by Hertzig (unpublished). We observe that ![]() $\operatorname {Lie}{\widehat {G}}$ has trivial center because
$\operatorname {Lie}{\widehat {G}}$ has trivial center because ![]() $l$ is very good for
$l$ is very good for ![]() ${\widehat {G}}$. The latter also excludes the case
${\widehat {G}}$. The latter also excludes the case ![]() $(k,\mathrm {type\ of\ }{\widehat {G}})= (\mathbb {F}_2,A_1)$. The cases
$(k,\mathrm {type\ of\ }{\widehat {G}})= (\mathbb {F}_2,A_1)$. The cases ![]() $(\mathbb {F}_5,A_1)$ and
$(\mathbb {F}_5,A_1)$ and ![]() $(\mathbb {F}_q,C_n)$,
$(\mathbb {F}_q,C_n)$, ![]() $q\in \{3,5,9\}$,
$q\in \{3,5,9\}$, ![]() $n\ge 2$, for
$n\ge 2$, for ![]() $(k,\mathrm {type\, of\, }{\widehat {G}})$ are ruled out by our list of exceptions. It follows from [Reference VölkleinVöl89, Theorem and Remarks] that
$(k,\mathrm {type\, of\, }{\widehat {G}})$ are ruled out by our list of exceptions. It follows from [Reference VölkleinVöl89, Theorem and Remarks] that ![]() $H^1({\widehat {G}}(k), \widehat {{\mathfrak g}}_{k}) = 0$.
$H^1({\widehat {G}}(k), \widehat {{\mathfrak g}}_{k}) = 0$.
Finally, we prove (iv). If ![]() ${\widehat {G}}$ is simply connected, then by [Reference Springer and SteinbergSS70, II.3.9] the group
${\widehat {G}}$ is simply connected, then by [Reference Springer and SteinbergSS70, II.3.9] the group ![]() $Z_{{\widehat {G}}}(h)$ is connected for all regular semisimple
$Z_{{\widehat {G}}}(h)$ is connected for all regular semisimple ![]() $h\in H$, and we are done. We now focus on the case where
$h\in H$, and we are done. We now focus on the case where ![]() ${\widehat {G}}$ of adjoint type, where we find a suitable
${\widehat {G}}$ of adjoint type, where we find a suitable ![]() $h$ using [Reference Feit and SeitzFS88]. The last paragraph explains how this gives (iv) for
$h$ using [Reference Feit and SeitzFS88]. The last paragraph explains how this gives (iv) for ![]() ${\widehat {G}}$ of any other type.
${\widehat {G}}$ of any other type.
Suppose that ![]() ${\widehat {G}}$ is of adjoint type. Then by [Reference Feit and SeitzFS88, Theorem 3.1] there exists a maximal torus
${\widehat {G}}$ is of adjoint type. Then by [Reference Feit and SeitzFS88, Theorem 3.1] there exists a maximal torus ![]() $T\subset {\widehat {G}}$ defined over
$T\subset {\widehat {G}}$ defined over ![]() $k$ such that the following statements hold:
$k$ such that the following statements hold:
(1) The group
 $T^+(k):={\widehat {G}}^+(k)\cap T(k)$ is cyclic. Let
$T^+(k):={\widehat {G}}^+(k)\cap T(k)$ is cyclic. Let  $h$ be a generator.
$h$ be a generator.(2) One has
 $Z_{{\widehat {G}}(k)}(h)=T(k)$, and the order of
$Z_{{\widehat {G}}(k)}(h)=T(k)$, and the order of  $h$ is given in [Reference Feit and SeitzFS88, Table III].
$h$ is given in [Reference Feit and SeitzFS88, Table III].(3) If
 ${\widehat {G}}$ is of type
${\widehat {G}}$ is of type  $A_n$, then
$A_n$, then  $T$ is quotient of a totally anisotropic maximal torus of
$T$ is quotient of a totally anisotropic maximal torus of  $\operatorname {GL}_{n+1}$ (over
$\operatorname {GL}_{n+1}$ (over  $k$) modulo its center, i.e.
$k$) modulo its center, i.e.  $T\cong \operatorname {Res}_{k^{(n+1)}}^k \mathbb {G}_m/\mathbb {G}_m$, the quotient of the Weil restriction of
$T\cong \operatorname {Res}_{k^{(n+1)}}^k \mathbb {G}_m/\mathbb {G}_m$, the quotient of the Weil restriction of  $\mathbb {G}_m$ from the unique degree-(
$\mathbb {G}_m$ from the unique degree-( $n+1$) extension
$n+1$) extension  $k^{(n+1)}$ of
$k^{(n+1)}$ of  $k$ to
$k$ to  $k$ modulo
$k$ modulo  $\mathbb {G}_m$.
$\mathbb {G}_m$.
Let ![]() $C:=Z_{{\widehat {G}}}(h)$, and let
$C:=Z_{{\widehat {G}}}(h)$, and let ![]() $\pi _0(C)=C/C^0$ be its component group scheme. It follows from [Reference SeitzSei83, 2.9 and its proof] that the identity component
$\pi _0(C)=C/C^0$ be its component group scheme. It follows from [Reference SeitzSei83, 2.9 and its proof] that the identity component ![]() $C^0$ is a (commuting) product of Chevalley groups over
$C^0$ is a (commuting) product of Chevalley groups over ![]() $k$ and of the center of
$k$ and of the center of ![]() $C^0$, and so from (1) above the natural map
$C^0$, and so from (1) above the natural map ![]() $T\to C^0$ must be an isomorphism because any Chevalley group has
$T\to C^0$ must be an isomorphism because any Chevalley group has ![]() $k$-points of order
$k$-points of order ![]() $l$. In particular,
$l$. In particular, ![]() $h$ is regular semisimple.
$h$ is regular semisimple.
Next we gather results on ![]() $\pi _0( C)$ that will allow us to identify it with the trivial group. By [Reference Springer and SteinbergSS70, Corollary II.4.4] there is an injective morphism of group schemes
$\pi _0( C)$ that will allow us to identify it with the trivial group. By [Reference Springer and SteinbergSS70, Corollary II.4.4] there is an injective morphism of group schemes ![]() $\pi _0(C)\to Z({\widehat {G}}^{\rm sc})$ to the center
$\pi _0(C)\to Z({\widehat {G}}^{\rm sc})$ to the center ![]() $Z({\widehat {G}}^{\rm sc})$ of
$Z({\widehat {G}}^{\rm sc})$ of ![]() ${\widehat {G}}^{\rm sc}$. Because
${\widehat {G}}^{\rm sc}$. Because ![]() $l$ is good for
$l$ is good for ![]() ${\widehat {G}}$, the finite commutative group scheme
${\widehat {G}}$, the finite commutative group scheme ![]() $Z({\widehat {G}}^{\rm sc})$ is étale over
$Z({\widehat {G}}^{\rm sc})$ is étale over ![]() $k$. The centers are completely known, and a list can be found, for instance, in [Reference Arias-de Reyna and BöckleAB, Table 1]. Using the Bruhat decomposition of
$k$. The centers are completely known, and a list can be found, for instance, in [Reference Arias-de Reyna and BöckleAB, Table 1]. Using the Bruhat decomposition of ![]() ${\widehat {G}}$ over
${\widehat {G}}$ over ![]() $\overline k$, and that
$\overline k$, and that ![]() $h$ is regular semisimple, it is not difficult to show that
$h$ is regular semisimple, it is not difficult to show that ![]() $C$ is a subgroup of the normalizer of
$C$ is a subgroup of the normalizer of ![]() $T$ in
$T$ in ![]() ${\widehat {G}}$ (over
${\widehat {G}}$ (over ![]() $\overline k$), and hence
$\overline k$), and hence ![]() $\pi _0(C)$ is a subgroup of the Weyl group of
$\pi _0(C)$ is a subgroup of the Weyl group of ![]() $G$. Moreover, by [Reference Springer and SteinbergSS70, I.2.11] one has a short exact sequence
$G$. Moreover, by [Reference Springer and SteinbergSS70, I.2.11] one has a short exact sequence
From (2) above we deduce that ![]() $T(k)\to C(k)$ is an isomorphism, and hence
$T(k)\to C(k)$ is an isomorphism, and hence ![]() $\pi _0( C)(k)$ is trivial.
$\pi _0( C)(k)$ is trivial.
Now suppose the type is ![]() $B_n$,
$B_n$, ![]() $C_n$,
$C_n$, ![]() $D_n$ or
$D_n$ or ![]() $E_7$. Then
$E_7$. Then ![]() $l$ cannot be
$l$ cannot be ![]() $2$, and so
$2$, and so ![]() $2$ divides the order of
$2$ divides the order of ![]() $k^\times$. It follows from the classification of the centers
$k^\times$. It follows from the classification of the centers ![]() $Z({\widehat {G}}^{\rm sc})$, that any non-trivial subgroup scheme will contain an element of exact order
$Z({\widehat {G}}^{\rm sc})$, that any non-trivial subgroup scheme will contain an element of exact order ![]() $2$. But then
$2$. But then ![]() $\pi _0( C)$ must be trivial, because we know already that
$\pi _0( C)$ must be trivial, because we know already that ![]() $\pi _0( C) (k)$ is trivial.
$\pi _0( C) (k)$ is trivial.
The types ![]() $E_8$,
$E_8$, ![]() $F_4$ and
$F_4$ and ![]() $G_2$ need not be considered, since here
$G_2$ need not be considered, since here ![]() $Z({\widehat {G}}^{\rm sc})$ is trivial and hence
$Z({\widehat {G}}^{\rm sc})$ is trivial and hence ![]() ${\widehat {G}}$ itself is simply connected. Next we consider type
${\widehat {G}}$ itself is simply connected. Next we consider type ![]() $E_6$, so that
$E_6$, so that ![]() $Z({\widehat {G}}^{\rm sc})\cong \mu _3$. Let
$Z({\widehat {G}}^{\rm sc})\cong \mu _3$. Let ![]() $q=\#k$. If
$q=\#k$. If ![]() $q \equiv 1 \pmod 3$, we can argue as in the previous paragraph to deduce that
$q \equiv 1 \pmod 3$, we can argue as in the previous paragraph to deduce that ![]() $\pi _0( C)$ is trivial. If, on the other hand,
$\pi _0( C)$ is trivial. If, on the other hand, ![]() $q \equiv -1 \pmod 3$, then from [Reference Feit and SeitzFS88, Table III] we find that
$q \equiv -1 \pmod 3$, then from [Reference Feit and SeitzFS88, Table III] we find that
so that the order of ![]() $h$ is not divisible by
$h$ is not divisible by ![]() $3$. It follows from [Reference Springer and SteinbergSS70, Corollary 4.6] that
$3$. It follows from [Reference Springer and SteinbergSS70, Corollary 4.6] that ![]() $\pi _0( C)$ is connected.
$\pi _0( C)$ is connected.
It remains to discuss the type ![]() $A_n$. For
$A_n$. For ![]() $n=1$, by (3) the element
$n=1$, by (3) the element ![]() $h$ is given as a diagonal matrix
$h$ is given as a diagonal matrix ![]() $\operatorname {diag}(x,x^q)$ in
$\operatorname {diag}(x,x^q)$ in ![]() $\operatorname {GL}_2/\mathbb {G}_m$ for some
$\operatorname {GL}_2/\mathbb {G}_m$ for some ![]() $x\in (k^{(2)} )^\times$ of order
$x\in (k^{(2)} )^\times$ of order ![]() $q^2-1$, so that
$q^2-1$, so that ![]() $h$ has order
$h$ has order ![]() $q+1$. Because
$q+1$. Because ![]() $C$ is spanned by
$C$ is spanned by ![]() $T$ and at most some Weyl group elements, we need to understand whether the unique non-trivial Weyl group element
$T$ and at most some Weyl group elements, we need to understand whether the unique non-trivial Weyl group element ![]() $w$ of
$w$ of ![]() ${\widehat {G}}=\operatorname {PGL}_2$ lies in
${\widehat {G}}=\operatorname {PGL}_2$ lies in ![]() $C$. The element
$C$. The element ![]() $w$ exchanges the entries of
$w$ exchanges the entries of ![]() $h$. If it would fix
$h$. If it would fix ![]() $h$, then
$h$, then ![]() $\operatorname {diag}(x,x^q)\equiv \operatorname {diag}(x^q,x)\pmod {\overline k^\times }$, so that there exists
$\operatorname {diag}(x,x^q)\equiv \operatorname {diag}(x^q,x)\pmod {\overline k^\times }$, so that there exists ![]() $a\in \overline k^\times$ with
$a\in \overline k^\times$ with ![]() $ax=x^q$ and
$ax=x^q$ and ![]() $ax^q=x$. This firstly implies
$ax^q=x$. This firstly implies ![]() $a\in \{\pm 1\}$, and then that the order of
$a\in \{\pm 1\}$, and then that the order of ![]() $x$ divides
$x$ divides ![]() $2(q-1)$. Because
$2(q-1)$. Because ![]() $q+1$ divides the order of
$q+1$ divides the order of ![]() $x$, this could only happen for
$x$, this could only happen for ![]() $q=2$, which is forbidden, since
$q=2$, which is forbidden, since ![]() $l$ is assumed to be very good for
$l$ is assumed to be very good for ![]() ${\widehat {G}}=\operatorname {PGL}_2$.
${\widehat {G}}=\operatorname {PGL}_2$.
Now suppose ![]() $n\ge 2$. Then
$n\ge 2$. Then ![]() $h$ is given by
$h$ is given by ![]() $\operatorname {diag}(x,x^q,\ldots,x^{q^n})\in \operatorname {GL}_{n+1}/\mathbb {G}_m(\overline k)$ for some
$\operatorname {diag}(x,x^q,\ldots,x^{q^n})\in \operatorname {GL}_{n+1}/\mathbb {G}_m(\overline k)$ for some ![]() $x\in (k^{(n+1)})^\times$ of order
$x\in (k^{(n+1)})^\times$ of order ![]() $q^{n+1}-1$. Let
$q^{n+1}-1$. Let ![]() $w$ be in the Weyl group of
$w$ be in the Weyl group of ![]() $\operatorname {PGL}_n$, which we identify with
$\operatorname {PGL}_n$, which we identify with ![]() $S_{n+1}$. Suppose that
$S_{n+1}$. Suppose that ![]() $h=w\circ h$, i.e. that
$h=w\circ h$, i.e. that ![]() $w$ is the image of an element of
$w$ is the image of an element of ![]() $C$. Because
$C$. Because ![]() $\pi _0( C)\subset Z(\operatorname {PGL}_{n+1})\cong \mu _{n+1}$ we may assume that
$\pi _0( C)\subset Z(\operatorname {PGL}_{n+1})\cong \mu _{n+1}$ we may assume that ![]() $w$ is cyclic of order dividing
$w$ is cyclic of order dividing ![]() $n+1$. Let
$n+1$. Let ![]() $r_1\ge \cdots r_s\ge 2$ be the lengths in the cycle decomposition of
$r_1\ge \cdots r_s\ge 2$ be the lengths in the cycle decomposition of ![]() $w$, and let
$w$, and let ![]() $r=\gcd (r_1,\ldots r_s)$, which is now a divisor of
$r=\gcd (r_1,\ldots r_s)$, which is now a divisor of ![]() $n+1$. As in the case
$n+1$. As in the case ![]() $n=1$, we find
$n=1$, we find ![]() $a\in \overline k^\times$ of order dividing
$a\in \overline k^\times$ of order dividing ![]() $r$ and such that
$r$ and such that ![]() $x^{q^{w(i)}}=ax^{q^i}$, or equivalently
$x^{q^{w(i)}}=ax^{q^i}$, or equivalently ![]() $x^{q^{w(i)}-q^i}=a$, for
$x^{q^{w(i)}-q^i}=a$, for ![]() $i=0,\ldots,n$.
$i=0,\ldots,n$.
To get further, let ![]() $t$ be a large Zsygmondy prime for
$t$ be a large Zsygmondy prime for ![]() $(q,n+1)$ in the sense of [Reference Feit and SeitzFS88, Theorem 2.1], i.e.
$(q,n+1)$ in the sense of [Reference Feit and SeitzFS88, Theorem 2.1], i.e. ![]() $t$ is a prime that divides
$t$ is a prime that divides ![]() $q^{n+1}-1$, that does not divide
$q^{n+1}-1$, that does not divide ![]() $q^m-1$ for
$q^m-1$ for ![]() $1\le m \le n$ and with either
$1\le m \le n$ and with either ![]() $t>n+1$ or
$t>n+1$ or ![]() $t^2|(q^{n+1}-1)$. We deduce that
$t^2|(q^{n+1}-1)$. We deduce that ![]() $t$ divides the order of
$t$ divides the order of ![]() $x^{q^{w(i)}-q^i}$ for any
$x^{q^{w(i)}-q^i}$ for any ![]() $i$ with
$i$ with ![]() $w(i)\neq i$, and it follows that
$w(i)\neq i$, and it follows that ![]() $t$ divides
$t$ divides ![]() $r$ and in turn
$r$ and in turn ![]() $n+1$, unless
$n+1$, unless ![]() $w$ is trivial. But then modulo the prime
$w$ is trivial. But then modulo the prime ![]() $t$ and using Fermat's little theorem we have
$t$ and using Fermat's little theorem we have
This contradicts that ![]() $t$ is a Zsygmondy prime for
$t$ is a Zsygmondy prime for ![]() $(q,n+1)$. Hence
$(q,n+1)$. Hence ![]() $w$ must be trivial and
$w$ must be trivial and ![]() $T=C$.
$T=C$.
Finally, for a general ![]() ${\widehat {G}}$ consider the central isogeny
${\widehat {G}}$ consider the central isogeny ![]() ${\widehat {G}}\to {\widehat {G}}^{\rm ad}$ to the adjoint quotient
${\widehat {G}}\to {\widehat {G}}^{\rm ad}$ to the adjoint quotient ![]() ${\widehat {G}}^{\rm ad}$ of
${\widehat {G}}^{\rm ad}$ of ![]() ${\widehat {G}}$. Let
${\widehat {G}}$. Let ![]() $H^{\rm ad}\subset {\widehat {G}}^{\rm ad}(k)$ be the image of
$H^{\rm ad}\subset {\widehat {G}}^{\rm ad}(k)$ be the image of ![]() $H$. Now the element
$H$. Now the element ![]() $h$ in
$h$ in ![]() $H^{ad,+}(k)$ from (1) above clearly lifts to some
$H^{ad,+}(k)$ from (1) above clearly lifts to some ![]() $h'\in {\widehat {G}}^+(k)$ with
$h'\in {\widehat {G}}^+(k)$ with ![]() $h'$ regular semisimple. Moreover, we have a left exact sequence
$h'$ regular semisimple. Moreover, we have a left exact sequence ![]() $0\to Z({\widehat {G}})\to Z_{{\widehat {G}}}(h')\to Z_{{\widehat {G}}^{\rm ad}}(h)$. In it,
$0\to Z({\widehat {G}})\to Z_{{\widehat {G}}}(h')\to Z_{{\widehat {G}}^{\rm ad}}(h)$. In it, ![]() $Z_{{\widehat {G}}^{\rm ad}}(h)$ is a maximal torus,
$Z_{{\widehat {G}}^{\rm ad}}(h)$ is a maximal torus, ![]() $Z_{{\widehat {G}}}(h')$ contains a maximal torus, and the center
$Z_{{\widehat {G}}}(h')$ contains a maximal torus, and the center ![]() $Z({\widehat {G}})$ lies in any maximal torus of
$Z({\widehat {G}})$ lies in any maximal torus of ![]() ${\widehat {G}}$. Hence
${\widehat {G}}$. Hence ![]() $Z_{{\widehat {G}}}(h')$ is a (maximal) torus, and thus connected.
$Z_{{\widehat {G}}}(h')$ is a (maximal) torus, and thus connected.
3.5 Taylor–Wiles primes
Following [Reference Böckle, Harris, Khare and ThorneBHKT19, Definition 5.16], we define a Taylor–Wiles datum for ![]() $\overline {\sigma }$ to be a pair
$\overline {\sigma }$ to be a pair ![]() $(Q, \{ \varphi _v \}_{v \in Q})$, where the following statements hold:
$(Q, \{ \varphi _v \}_{v \in Q})$, where the following statements hold:
•
 $Q$ is a finite set of places
$Q$ is a finite set of places  $v$ of
$v$ of  $K$ such that
$K$ such that  $\overline {\sigma }(\operatorname {Frob}_v)$ is regular semisimple and
$\overline {\sigma }(\operatorname {Frob}_v)$ is regular semisimple and  $q_v \equiv 1 \text { mod }\ell$
$q_v \equiv 1 \text { mod }\ell$• For each
 $v \in Q$,
$v \in Q$,  $\varphi _v : {\widehat {T}}_k \cong Z_{\widehat {G}}(\overline {\sigma }(\operatorname {Frob}_v))$ is a choice of inner isomorphism. In particular, this forces
$\varphi _v : {\widehat {T}}_k \cong Z_{\widehat {G}}(\overline {\sigma }(\operatorname {Frob}_v))$ is a choice of inner isomorphism. In particular, this forces  $Z_{\widehat {G}}(\overline {\sigma }(\operatorname {Frob}_v))$ to be connected.
$Z_{\widehat {G}}(\overline {\sigma }(\operatorname {Frob}_v))$ to be connected.
For a global deformation problem ![]() ${\mathcal {D}} = (S, \{{\mathcal {D}}_v\}_{v \in S})$ and a Taylor–Wiles datum
${\mathcal {D}} = (S, \{{\mathcal {D}}_v\}_{v \in S})$ and a Taylor–Wiles datum ![]() $(Q, \{ \varphi _v \}_{v \in Q})$ with
$(Q, \{ \varphi _v \}_{v \in Q})$ with ![]() $Q \cap S = \emptyset$, we define a new global deformation problem
$Q \cap S = \emptyset$, we define a new global deformation problem ![]() ${\mathcal {D}}_Q = (S \cup Q, ({\mathcal {D}}_Q)_v )$ with
${\mathcal {D}}_Q = (S \cup Q, ({\mathcal {D}}_Q)_v )$ with
 \[ ({\mathcal{D}}_Q)_v = \begin{cases} {\mathcal{D}}_v & v \in S, \\ {\mathcal{D}}_{{\overline{\sigma}}, v}^{\square} & v \in Q. \end{cases} \]
\[ ({\mathcal{D}}_Q)_v = \begin{cases} {\mathcal{D}}_v & v \in S, \\ {\mathcal{D}}_{{\overline{\sigma}}, v}^{\square} & v \in Q. \end{cases} \]
The proposition below guarantees the existence of sets of Taylor–Wiles primes suitable for patching, generalizing [Reference Böckle, Harris, Khare and ThorneBHKT19, Proposition 5.19]. Actually there are some typos in the statement and proof of [Reference Böckle, Harris, Khare and ThorneBHKT19, Proposition 5.19]; the argument below can be used to rectify them.
Proposition 3.9 Suppose that the group ![]() $\overline {\rho }(\Gamma _{K(\zeta _\ell )}) \subset {\widehat {G}}(k)$ is
$\overline {\rho }(\Gamma _{K(\zeta _\ell )}) \subset {\widehat {G}}(k)$ is ![]() ${\widehat {G}}$-abundant. Let
${\widehat {G}}$-abundant. Let ![]() ${\mathcal {D}} := (S, \{{\mathcal {D}}_v\}_{v \in S})$ be a global deformation problem such that for each
${\mathcal {D}} := (S, \{{\mathcal {D}}_v\}_{v \in S})$ be a global deformation problem such that for each ![]() $v \in S$ the local deformation problem
$v \in S$ the local deformation problem ![]() ${\mathcal {D}}_v$ is balanced, with corresponding subspace
${\mathcal {D}}_v$ is balanced, with corresponding subspace ![]() $L_v \subset H^1({\Gamma _{K_v}}, {\rm ad}({\overline {\sigma }}))$. Then for each
$L_v \subset H^1({\Gamma _{K_v}}, {\rm ad}({\overline {\sigma }}))$. Then for each ![]() $j \geq 1$, there is a Taylor–Wiles datum
$j \geq 1$, there is a Taylor–Wiles datum ![]() $(Q, \{ \varphi _v \}_{v \in Q})$, satisfying the following conditions:
$(Q, \{ \varphi _v \}_{v \in Q})$, satisfying the following conditions:
(i)
 $Q \cap S = \emptyset$, and for each
$Q \cap S = \emptyset$, and for each  $v \in Q$, we have
$v \in Q$, we have  $q_v \equiv 1 \text { mod }\ell ^j$, and
$q_v \equiv 1 \text { mod }\ell ^j$, and
 \[ \# Q = h^1_{\mathcal{D}}(\Gamma_{K, S}, {\rm ad}({\overline{\sigma}})) = h^1_{{\mathcal{D}}^{\perp}}(\Gamma_{K, S}, {\rm ad}({\overline{\sigma}})^\vee(1)). \]
\[ \# Q = h^1_{\mathcal{D}}(\Gamma_{K, S}, {\rm ad}({\overline{\sigma}})) = h^1_{{\mathcal{D}}^{\perp}}(\Gamma_{K, S}, {\rm ad}({\overline{\sigma}})^\vee(1)). \]
(ii) We have
 $h^1_{{\mathcal {D}}_Q}(\Gamma _{K, S \cup Q}, {\rm ad}({\overline {\sigma }})^\vee (1)) = 0$.
$h^1_{{\mathcal {D}}_Q}(\Gamma _{K, S \cup Q}, {\rm ad}({\overline {\sigma }})^\vee (1)) = 0$.(iii) There exists a surjection
 ${\mathcal {O}} \unicode{x27E6} X_1, \ldots, X_g \unicode{x27E7} \twoheadrightarrow R_{{\overline {\sigma }}, S \cup Q, {\mathcal {D}}}$ with
${\mathcal {O}} \unicode{x27E6} X_1, \ldots, X_g \unicode{x27E7} \twoheadrightarrow R_{{\overline {\sigma }}, S \cup Q, {\mathcal {D}}}$ with  $g = h^1_{{\mathcal {D}}}(\Gamma _{K, S}, {\rm ad}({\overline {\sigma }})) + (r-1)\# Q$, where
$g = h^1_{{\mathcal {D}}}(\Gamma _{K, S}, {\rm ad}({\overline {\sigma }})) + (r-1)\# Q$, where  $r = \operatorname {rank} {\widehat {G}}$.
$r = \operatorname {rank} {\widehat {G}}$.
Proof. If ![]() $S \cup Q = \emptyset$ then (i) and (ii) are vacuous and (iii) is an immediate consequence of Proposition 3.6(ii). For the rest of the proof, we assume that
$S \cup Q = \emptyset$ then (i) and (ii) are vacuous and (iii) is an immediate consequence of Proposition 3.6(ii). For the rest of the proof, we assume that ![]() $S \cup Q$ is non-empty.
$S \cup Q$ is non-empty.
We apply [Reference ČesnaviciusČes15, Theorem 6.2], using that ![]() $H^0(\Gamma _{K, S \cup Q}, {\rm ad} ({\overline {\sigma }})(1)) = H^0(\Gamma _{K, S \cup Q}, {\rm ad} ({\overline {\sigma }})) = 0$ by the abundance assumption, and the local and global Euler characteristic formulas (note our assumption that
$H^0(\Gamma _{K, S \cup Q}, {\rm ad} ({\overline {\sigma }})(1)) = H^0(\Gamma _{K, S \cup Q}, {\rm ad} ({\overline {\sigma }})) = 0$ by the abundance assumption, and the local and global Euler characteristic formulas (note our assumption that ![]() $S \cup Q$ is non-empty) to deduce that
$S \cup Q$ is non-empty) to deduce that
The assumption that ![]() ${\mathcal {D}}_v$ is balanced for all
${\mathcal {D}}_v$ is balanced for all ![]() $v \in S$ implies that
$v \in S$ implies that ![]() $\dim {\mathcal {L}}_v - h^0(G_{F_v}, {\rm ad} ({\overline {\sigma }})) = 0$ for all
$\dim {\mathcal {L}}_v - h^0(G_{F_v}, {\rm ad} ({\overline {\sigma }})) = 0$ for all ![]() $v \in S$. We claim that once we can arrange (i) and (ii), then (iii) follows automatically. Indeed, if
$v \in S$. We claim that once we can arrange (i) and (ii), then (iii) follows automatically. Indeed, if ![]() $h^1_{{\mathcal {D}}_Q^{\perp }}(\Gamma _{K, S \cup Q} , {\rm ad} ({\overline {\sigma }})^{\vee }(1))$ vanishes then (3.3) implies that
$h^1_{{\mathcal {D}}_Q^{\perp }}(\Gamma _{K, S \cup Q} , {\rm ad} ({\overline {\sigma }})^{\vee }(1))$ vanishes then (3.3) implies that
from which (iii) follows by invoking Proposition 3.6.
It therefore remains to show that ![]() $Q$ can be chosen so that
$Q$ can be chosen so that
 \begin{align*} &H^1_{{\mathcal{D}}_Q^{\perp}}(\Gamma_{K, S \cup Q} , {\rm ad}({\overline{\sigma}})^{\vee}(1))\\ &\quad :=\ker \bigg( H^1(\Gamma_{K, S \cup Q} , {\rm ad}({\overline{\sigma}})^{\vee}(1)) \rightarrow \bigg( \bigoplus_{v \in S} \frac{H^1(K_v, {\rm ad}({\overline{\sigma}})^{\vee}(1)) }{ L_v} \oplus \bigoplus_{v \in Q} H^1(K_v, {\rm ad}({\overline{\sigma}})^{\vee}(1)) \bigg) \bigg) \end{align*}
\begin{align*} &H^1_{{\mathcal{D}}_Q^{\perp}}(\Gamma_{K, S \cup Q} , {\rm ad}({\overline{\sigma}})^{\vee}(1))\\ &\quad :=\ker \bigg( H^1(\Gamma_{K, S \cup Q} , {\rm ad}({\overline{\sigma}})^{\vee}(1)) \rightarrow \bigg( \bigoplus_{v \in S} \frac{H^1(K_v, {\rm ad}({\overline{\sigma}})^{\vee}(1)) }{ L_v} \oplus \bigoplus_{v \in Q} H^1(K_v, {\rm ad}({\overline{\sigma}})^{\vee}(1)) \bigg) \bigg) \end{align*}
vanishes. By a comparison of inflation-restriction exact sequences, the inflation map ![]() $H^1(\Gamma _{K, S }, {\rm ad}({\overline {\sigma }})^{\vee }(1)) \rightarrow H^1(\Gamma _{K, S \cup Q}, {\rm ad}({\overline {\sigma }})^{\vee }(1))$ takes
$H^1(\Gamma _{K, S }, {\rm ad}({\overline {\sigma }})^{\vee }(1)) \rightarrow H^1(\Gamma _{K, S \cup Q}, {\rm ad}({\overline {\sigma }})^{\vee }(1))$ takes
 \begin{align*} &\ker \bigg( H^1(\Gamma_{K, S} , {\rm ad}({\overline{\sigma}})^{\vee}(1)) \rightarrow \bigoplus_{v \in Q} H^1(k(v), {\rm ad}({\overline{\sigma}})^{\vee}(1)) \bigg)\\ &\quad \xrightarrow{\sim}\ker \bigg( H^1(\Gamma_{K, S \cup Q} , {\rm ad}({\overline{\sigma}})^{\vee}(1)) \rightarrow \bigoplus_{v \in Q} H^1(K_v, {\rm ad}({\overline{\sigma}})^{\vee}(1)) \bigg) . \end{align*}
\begin{align*} &\ker \bigg( H^1(\Gamma_{K, S} , {\rm ad}({\overline{\sigma}})^{\vee}(1)) \rightarrow \bigoplus_{v \in Q} H^1(k(v), {\rm ad}({\overline{\sigma}})^{\vee}(1)) \bigg)\\ &\quad \xrightarrow{\sim}\ker \bigg( H^1(\Gamma_{K, S \cup Q} , {\rm ad}({\overline{\sigma}})^{\vee}(1)) \rightarrow \bigoplus_{v \in Q} H^1(K_v, {\rm ad}({\overline{\sigma}})^{\vee}(1)) \bigg) . \end{align*}
Therefore it suffices by induction to show that for any ![]() $j$ and any non-zero
$j$ and any non-zero ![]() $[\psi ] \in H^1(\Gamma _{K, S}, \widehat {\mathfrak {g}}_k^{\vee }(1))$, we can find infinitely many places
$[\psi ] \in H^1(\Gamma _{K, S}, \widehat {\mathfrak {g}}_k^{\vee }(1))$, we can find infinitely many places ![]() $v \not \in S$ of
$v \not \in S$ of ![]() $K$ such that
$K$ such that ![]() $q_v \equiv 1 \text { mod }\ell ^j$,
$q_v \equiv 1 \text { mod }\ell ^j$, ![]() $\overline {\rho }(\operatorname {Frob}_v)$ is regular semisimple with connected centralizer in
$\overline {\rho }(\operatorname {Frob}_v)$ is regular semisimple with connected centralizer in ![]() ${\widehat {G}}_k$, and
${\widehat {G}}_k$, and ![]() $\operatorname {res}_{K_v} [\psi ] \neq 0$. The rest of the argument concludes exactly as in [Reference Böckle, Harris, Khare and ThorneBHKT19, Proof of Proposition 5.19].
$\operatorname {res}_{K_v} [\psi ] \neq 0$. The rest of the argument concludes exactly as in [Reference Böckle, Harris, Khare and ThorneBHKT19, Proof of Proposition 5.19].
4. Automorphy lifting
In this section we prove the automorphy lifting theorem that will be used to deduce cyclic base change. Such automorphy lifting theorems have been the subject of much study over number fields, and our proof employs similar techniques, but we are able to obtain results for more general groups thanks to the different numerical behavior of the Euler characteristics of function fields.
To put our results in context, we compare them to [Reference Böckle, Harris, Khare and ThorneBHKT19, Theorem 8.20], which handled everywhere unramified Galois representations. The main novelty of the present situation is that we need to implement automorphy lifting for arbitrarily ramified residual representations. In this section we use the Taylor–Wiles method to prove an automorphy lifting theorem (Theorem 4.6) whenever one knows that all the local deformation problems are well behaved (e.g. formally smooth). In the unramified case it was easy to see that the unramified local deformation problem is formally smooth; in the next section we give a suitable extension to unrestricted deformations for ramified representations, when ![]() $\ell$ is large enough.
$\ell$ is large enough.
4.1 Spaces of automorphic forms
We define integral spaces of automorphic forms as in [Reference Böckle, Harris, Khare and ThorneBHKT19, § 8.1]. For any open subgroup ![]() $U \subset G(\widehat {{\mathcal {O}}})$ and any
$U \subset G(\widehat {{\mathcal {O}}})$ and any ![]() $\mathbb {Z}[1/p]$-algebra
$\mathbb {Z}[1/p]$-algebra ![]() $R$, we define:
$R$, we define:
•
 $C(U, R)$ to be the
$C(U, R)$ to be the  $R$-module of functions
$R$-module of functions  $f : G(K) \backslash G({\mathbb {A}}_K) / U \to R$;
$f : G(K) \backslash G({\mathbb {A}}_K) / U \to R$;•
 $C_c(U, R) \subset C(U, R)$ to be the
$C_c(U, R) \subset C(U, R)$ to be the  $R$-submodule of functions
$R$-submodule of functions  $f$ which have finite support; and
$f$ which have finite support; and•
 $C_{\mathrm {cusp}}(U, R)$ to be the
$C_{\mathrm {cusp}}(U, R)$ to be the  $R$-submodule of functions
$R$-submodule of functions  $f$ which are cuspidal, in the sense that for all proper parabolic subgroups
$f$ which are cuspidal, in the sense that for all proper parabolic subgroups  $P \subset G$ and for all
$P \subset G$ and for all  $g \in G({\mathbb {A}}_K)$, the integral
vanishes, where
$g \in G({\mathbb {A}}_K)$, the integral
vanishes, where \[ \int_{n \in N(K) \backslash N({\mathbb{A}}_K)} f(ng)\, dn \]
\[ \int_{n \in N(K) \backslash N({\mathbb{A}}_K)} f(ng)\, dn \]
 $N$ is the unipotent radical of
$N$ is the unipotent radical of  $P$.
$P$.
This last integral is normalized by endowing ![]() $N(K) \backslash N({\mathbb {A}}_K)$ with its probability Haar measure (which makes sense because we are assuming that
$N(K) \backslash N({\mathbb {A}}_K)$ with its probability Haar measure (which makes sense because we are assuming that ![]() $p$ is a unit in
$p$ is a unit in ![]() $R$). We have
$R$). We have ![]() $C_{\operatorname {cusp}}(U,R) \subset C_{c}(U, R)$ by [Reference Böckle, Harris, Khare and ThorneBHKT19, Proposition 8.2].
$C_{\operatorname {cusp}}(U,R) \subset C_{c}(U, R)$ by [Reference Böckle, Harris, Khare and ThorneBHKT19, Proposition 8.2].
We define ![]() $C_{\operatorname {cusp}}(G,R) := \varinjlim _U C_{\mathrm {cusp}}(U, R)$.
$C_{\operatorname {cusp}}(G,R) := \varinjlim _U C_{\mathrm {cusp}}(U, R)$.
Let ![]() $N = \sum _v n_v \cdot v \subset X$ be an effective divisor and let
$N = \sum _v n_v \cdot v \subset X$ be an effective divisor and let ![]() $U(N) := \ker ( \prod _v G({\mathcal {O}}_{K_v}) \to G({\mathcal {O}}_N) )$. The underlying set of places
$U(N) := \ker ( \prod _v G({\mathcal {O}}_{K_v}) \to G({\mathcal {O}}_N) )$. The underlying set of places ![]() $|N| = \bigcup _{n_v>0} \{v\}$ will play the role of the set
$|N| = \bigcup _{n_v>0} \{v\}$ will play the role of the set ![]() $S$ from § 3.
$S$ from § 3.
4.2 The excursion algebra and Lafforgue's parametrization
For the remainder of this section we choose a prime ![]() $\ell \neq p$ and coefficient field
$\ell \neq p$ and coefficient field ![]() $E \subset \overline {{\mathbb {Q}}}_\ell$. For
$E \subset \overline {{\mathbb {Q}}}_\ell$. For ![]() $R \in \{k, {\mathcal {O}},E\}$ we denote by
$R \in \{k, {\mathcal {O}},E\}$ we denote by ![]() ${\mathcal {B}}(U(N), R)$ the
${\mathcal {B}}(U(N), R)$ the ![]() $R$-subalgebra of
$R$-subalgebra of ![]() $\operatorname {End}_{R}(C_{\mathrm {cusp}}(U(N), R))$ generated by V. Lafforgue's excursion operators, as in [Reference Böckle, Harris, Khare and ThorneBHKT19, § 8.4]. For any fixed
$\operatorname {End}_{R}(C_{\mathrm {cusp}}(U(N), R))$ generated by V. Lafforgue's excursion operators, as in [Reference Böckle, Harris, Khare and ThorneBHKT19, § 8.4]. For any fixed ![]() $N$, this is a finite
$N$, this is a finite ![]() $R$-algebra. The Hecke operators
$R$-algebra. The Hecke operators ![]() $T_{V,v}$ as lying in
$T_{V,v}$ as lying in ![]() ${\mathcal {B}}(U(N), R)$, for
${\mathcal {B}}(U(N), R)$, for ![]() $v \notin |N|$ and
$v \notin |N|$ and ![]() $V$ a representation of
$V$ a representation of ![]() ${\widehat {G}}$, are defined as in [Reference Böckle, Harris, Khare and ThorneBHKT19].
${\widehat {G}}$, are defined as in [Reference Böckle, Harris, Khare and ThorneBHKT19].
The points of ![]() $\operatorname {Spec} {\mathcal {B}}(U(N),R)$ are naturally identified with semisimple
$\operatorname {Spec} {\mathcal {B}}(U(N),R)$ are naturally identified with semisimple ![]() $L$-parameters, in a manner that we will presently review. Combining [Reference Böckle, Harris, Khare and ThorneBHKT19, Corollaries 8.6, 8.11], we have the following (with notation as in those corollaries).
$L$-parameters, in a manner that we will presently review. Combining [Reference Böckle, Harris, Khare and ThorneBHKT19, Corollaries 8.6, 8.11], we have the following (with notation as in those corollaries).
Theorem 4.1 Let ![]() $R = E$ or
$R = E$ or ![]() $k$ and
$k$ and ![]() $\mathfrak {m} \subset {\mathcal {B}}(U(N),R)$ be a maximal ideal. Fix an embedding
$\mathfrak {m} \subset {\mathcal {B}}(U(N),R)$ be a maximal ideal. Fix an embedding ![]() ${\mathcal {B}}(U(N),R)/\mathfrak {m} \hookrightarrow \overline {R}$. Then the following statements hold:
${\mathcal {B}}(U(N),R)/\mathfrak {m} \hookrightarrow \overline {R}$. Then the following statements hold:
(i) There exists a continuous, absolutely
 ${\widehat {G}}$-completely reducible representation
${\widehat {G}}$-completely reducible representation  $\sigma _{\mathfrak {m}} : \Gamma _K \to {\widehat {G}}( \overline {R} )$ satisfying the following condition: for all excursion operators
$\sigma _{\mathfrak {m}} : \Gamma _K \to {\widehat {G}}( \overline {R} )$ satisfying the following condition: for all excursion operators  $S_{I, (\gamma _i)_{i \in I}, f}$, we have
(4.1)
$S_{I, (\gamma _i)_{i \in I}, f}$, we have
(4.1) \begin{equation} f( (\sigma_{\mathfrak{m}}(\gamma_i))_{i \in I}) = S_{I, (\gamma_i)_{i \in I}, f} \text{ mod }{\mathfrak{m}}. \end{equation}
\begin{equation} f( (\sigma_{\mathfrak{m}}(\gamma_i))_{i \in I}) = S_{I, (\gamma_i)_{i \in I}, f} \text{ mod }{\mathfrak{m}}. \end{equation}(ii) The representation
 $\sigma _{\mathfrak {m}}$ is uniquely determined up to
$\sigma _{\mathfrak {m}}$ is uniquely determined up to  ${\widehat {G}}(\overline {R})$-conjugacy by (4.1).
${\widehat {G}}(\overline {R})$-conjugacy by (4.1).(iii) The representation
 $\sigma _{\mathfrak {m}}$ is unramified outside
$\sigma _{\mathfrak {m}}$ is unramified outside  $|N|$. If
$|N|$. If  $v \not \in |N|$, then it satisfies the expected local–global compatibility relation at
$v \not \in |N|$, then it satisfies the expected local–global compatibility relation at  $v$: for all irreducible representations
$v$: for all irreducible representations  $V$ of
$V$ of  ${\widehat {G}}_{\overline {{\mathbb {Q}}}_\ell }$, we have
${\widehat {G}}_{\overline {{\mathbb {Q}}}_\ell }$, we have  $T_{V, v} \in {\mathcal {B}}(U(N), R)$ and
$T_{V, v} \in {\mathcal {B}}(U(N), R)$ and
 \[ \chi_V( \sigma_{\mathfrak{m}}(\operatorname{Frob}_v) ) = T_{V, v} \in {\mathcal{B}}(U(N), R)/\mathfrak{m}. \]
\[ \chi_V( \sigma_{\mathfrak{m}}(\operatorname{Frob}_v) ) = T_{V, v} \in {\mathcal{B}}(U(N), R)/\mathfrak{m}. \]
For ![]() $R \in \{k, E \}$ and any
$R \in \{k, E \}$ and any ![]() $N$, V. Lafforgue constructs a decomposition of
$N$, V. Lafforgue constructs a decomposition of ![]() $C_{\operatorname {cusp}}(U(N), \overline {R})$ into summands indexed by
$C_{\operatorname {cusp}}(U(N), \overline {R})$ into summands indexed by ![]() $L$-parameters
$L$-parameters ![]() $\sigma \in H^1(\Gamma _{K,N} , \widehat {G}(\overline {R}))$. More specifically, this decomposition comes from the generalized eigenspace decomposition for the action of
$\sigma \in H^1(\Gamma _{K,N} , \widehat {G}(\overline {R}))$. More specifically, this decomposition comes from the generalized eigenspace decomposition for the action of ![]() ${\mathcal {B}}(U(N), R)$ on
${\mathcal {B}}(U(N), R)$ on ![]() $C_{\operatorname {cusp}}(U(N), R)$. If
$C_{\operatorname {cusp}}(U(N), R)$. If ![]() $\Pi \subset C_{\operatorname {cusp}}(G, \overline {R})$ is a subspace such that
$\Pi \subset C_{\operatorname {cusp}}(G, \overline {R})$ is a subspace such that ![]() $\Pi ^{U(N)}$ is stable under the
$\Pi ^{U(N)}$ is stable under the ![]() ${\mathcal {B}}(U(N), \overline {R})$-action and supported over a unique maximal ideal, we will denote this maximal ideal by
${\mathcal {B}}(U(N), \overline {R})$-action and supported over a unique maximal ideal, we will denote this maximal ideal by ![]() ${\mathfrak m} = {\mathfrak m}_\Pi \subset {\mathcal {B}}(U(N), \overline {R})$. The corresponding
${\mathfrak m} = {\mathfrak m}_\Pi \subset {\mathcal {B}}(U(N), \overline {R})$. The corresponding ![]() $L$-parameter is then denoted
$L$-parameter is then denoted ![]() $\sigma _{\Pi } := \sigma _{{\mathfrak m}}$, and we say that
$\sigma _{\Pi } := \sigma _{{\mathfrak m}}$, and we say that ![]() $\sigma _{\Pi }$ is the
$\sigma _{\Pi }$ is the ![]() $L$-parameter attached to
$L$-parameter attached to ![]() $\Pi$. This assignment
$\Pi$. This assignment ![]() $\Pi \mapsto \sigma _{\Pi }$ is independent of the choice of
$\Pi \mapsto \sigma _{\Pi }$ is independent of the choice of ![]() $N$ such that
$N$ such that ![]() $\Pi ^{U(N)} \neq 0$. This correspondence has the property that
$\Pi ^{U(N)} \neq 0$. This correspondence has the property that ![]() $\Pi$ and
$\Pi$ and ![]() $\sigma _{\Pi }$ match under the local Langlands correspondence at all places where
$\sigma _{\Pi }$ match under the local Langlands correspondence at all places where ![]() $\Pi$ is unramified, although we caution that this property does not characterize it for general groups.
$\Pi$ is unramified, although we caution that this property does not characterize it for general groups.
Remark 4.2 (A one-to-finite correspondence)
We continue to assume ![]() $R \in \{k, E\}$. Not every irreducible
$R \in \{k, E\}$. Not every irreducible ![]() $G(\mathbb {A})$-subspace
$G(\mathbb {A})$-subspace ![]() $\Pi$ of
$\Pi$ of ![]() $C_{\operatorname {cusp}}(G,R)$ is attached to an
$C_{\operatorname {cusp}}(G,R)$ is attached to an ![]() $L$-parameter
$L$-parameter ![]() $\sigma _{\Pi }$ in the sense of the previous paragraph. The notation
$\sigma _{\Pi }$ in the sense of the previous paragraph. The notation ![]() $\sigma _{\Pi }$ will only be used if
$\sigma _{\Pi }$ will only be used if ![]() $\Pi$ is attached to
$\Pi$ is attached to ![]() $\sigma _{\Pi }$ in the manner of the above paragraph. However, we do have the following construction which produces a finite set of
$\sigma _{\Pi }$ in the manner of the above paragraph. However, we do have the following construction which produces a finite set of ![]() $L$-parameters, each of which matches
$L$-parameters, each of which matches ![]() $\Pi$ locally at all unramified places.
$\Pi$ locally at all unramified places.
Let ![]() $C_{\operatorname {cusp}}(G,R)[\Pi ]$ be the
$C_{\operatorname {cusp}}(G,R)[\Pi ]$ be the ![]() $\Pi$-isotypic subspace of
$\Pi$-isotypic subspace of ![]() $C_{\operatorname {cusp}}(G,R)$ for the
$C_{\operatorname {cusp}}(G,R)$ for the ![]() $G(\mathbb {A}_K)$-action. Then the space
$G(\mathbb {A}_K)$-action. Then the space ![]() $C_{\operatorname {cusp}}(G,R)[\Pi ]^{U(N)}$ is stable under the action of
$C_{\operatorname {cusp}}(G,R)[\Pi ]^{U(N)}$ is stable under the action of ![]() ${\mathcal {B}}(U(N), R)$, and finite-dimensional for every
${\mathcal {B}}(U(N), R)$, and finite-dimensional for every ![]() $N$. We define
$N$. We define ![]() $\underline {\rho }_{\Pi }$ to be the finite set of
$\underline {\rho }_{\Pi }$ to be the finite set of ![]() $L$-parameters corresponding to the maximal ideals of
$L$-parameters corresponding to the maximal ideals of ![]() ${\mathcal {B}}(U(N), R)$ in the support of
${\mathcal {B}}(U(N), R)$ in the support of ![]() $C_{\operatorname {cusp}}(G,R)[\Pi ]^{U(N)}$. Since each
$C_{\operatorname {cusp}}(G,R)[\Pi ]^{U(N)}$. Since each ![]() $\sigma \in \underline {\rho }_{\Pi }$ is associated to an automorphic representation isomorphic to
$\sigma \in \underline {\rho }_{\Pi }$ is associated to an automorphic representation isomorphic to ![]() $\Pi$ at all local places, in particular the unramified ones, we have that each
$\Pi$ at all local places, in particular the unramified ones, we have that each ![]() $\rho$ matches
$\rho$ matches ![]() $\Pi$ at every unramified place under the (unramified) local Langlands correspondence.
$\Pi$ at every unramified place under the (unramified) local Langlands correspondence.
We note that by [Reference Böckle, Harris, Khare and ThorneBHKT19, Proposition 6.4], if some ![]() $\sigma \in \underline {\rho }_{\Pi }$ has Zariski dense image in
$\sigma \in \underline {\rho }_{\Pi }$ has Zariski dense image in ![]() $\widehat {G}$, then in fact
$\widehat {G}$, then in fact ![]() $\underline {\rho }_{\Pi }$ is a singleton, so
$\underline {\rho }_{\Pi }$ is a singleton, so ![]() $\underline {\rho }_{\Pi } = \{ \sigma _{\Pi }\}$.
$\underline {\rho }_{\Pi } = \{ \sigma _{\Pi }\}$.
In § 5 we will need to work with collections of representations with ![]() $\overline {\mathbb {Q}}_{\ell }$ or
$\overline {\mathbb {Q}}_{\ell }$ or ![]() $\overline {{\mathbb {F}}}_\ell$ coefficients, as
$\overline {{\mathbb {F}}}_\ell$ coefficients, as ![]() $\ell$ varies. We may therefore write
$\ell$ varies. We may therefore write ![]() $\sigma _{\Pi, \ell }$ for
$\sigma _{\Pi, \ell }$ for ![]() $\sigma _{\Pi }$ and
$\sigma _{\Pi }$ and ![]() ${\overline {\sigma }}_{\Pi,\ell }$ for
${\overline {\sigma }}_{\Pi,\ell }$ for ![]() ${\overline {\sigma }}_\Pi$ when it is necessary to specify the coefficients.
${\overline {\sigma }}_\Pi$ when it is necessary to specify the coefficients.
Definition 4.3 Let ![]() $\Pi$ be a cuspidal automorphic representation of
$\Pi$ be a cuspidal automorphic representation of ![]() $G({\mathbb {A}}_K)$ defined over a number field
$G({\mathbb {A}}_K)$ defined over a number field ![]() $L$. We say that the Mumford–Tate group of
$L$. We say that the Mumford–Tate group of ![]() $\Pi$ is
$\Pi$ is ![]() ${\widehat {G}}$ if for some (equivalently, every) prime
${\widehat {G}}$ if for some (equivalently, every) prime ![]() $\ell \neq p$ and embedding
$\ell \neq p$ and embedding ![]() $L \to \overline {{\mathbb {Q}}}_\ell$, the image of
$L \to \overline {{\mathbb {Q}}}_\ell$, the image of ![]() $\sigma _{\Pi, \ell }$ is Zariski dense in
$\sigma _{\Pi, \ell }$ is Zariski dense in ![]() ${\widehat {G}}$. As explained in Remark 4.2, this notion does not depend on the choice of
${\widehat {G}}$. As explained in Remark 4.2, this notion does not depend on the choice of ![]() $\sigma _{\Pi, \ell } \in \underline {\rho }_{\Pi \otimes _L \overline {{\mathbb {Q}}}_\ell }$.
$\sigma _{\Pi, \ell } \in \underline {\rho }_{\Pi \otimes _L \overline {{\mathbb {Q}}}_\ell }$.
4.3 Automorphy lifting theorems
Let ![]() $\chi \colon {\mathcal {B}}(U(N), {\mathcal {O}}) \rightarrow \overline {\mathbb {Z}}_{\ell }$ be a homomorphism. After possibly enlarging
$\chi \colon {\mathcal {B}}(U(N), {\mathcal {O}}) \rightarrow \overline {\mathbb {Z}}_{\ell }$ be a homomorphism. After possibly enlarging ![]() $E$, we can assume that
$E$, we can assume that ![]() $\chi$ takes values in
$\chi$ takes values in ![]() ${\mathcal {O}}$. Let
${\mathcal {O}}$. Let ![]() $\mathfrak {m} \subset {\mathcal {B}}(U(N), {\mathcal {O}})$ be the maximal ideal which is the kernel of the composition of
$\mathfrak {m} \subset {\mathcal {B}}(U(N), {\mathcal {O}})$ be the maximal ideal which is the kernel of the composition of ![]() $\chi$ with
$\chi$ with ![]() ${\mathcal {O}} \rightarrow k$, and
${\mathcal {O}} \rightarrow k$, and ![]() ${\overline {\sigma }}_{\mathfrak {m}}$ the Galois representation corresponding to
${\overline {\sigma }}_{\mathfrak {m}}$ the Galois representation corresponding to ![]() $\mathfrak {m}$ under Theorem 4.1. After possibly further enlarging
$\mathfrak {m}$ under Theorem 4.1. After possibly further enlarging ![]() $E$, we can assume that
$E$, we can assume that ![]() ${\overline {\sigma }}_{\mathfrak {m}}$ takes values in
${\overline {\sigma }}_{\mathfrak {m}}$ takes values in ![]() $\widehat {G}(k)$.
$\widehat {G}(k)$.
With Definition 3.7 in mind, we make the following assumptions on ![]() ${\overline {\sigma }}_{\mathfrak {m}}$:
${\overline {\sigma }}_{\mathfrak {m}}$:
(i)
 $\ell \nmid \# W$. This implies, in particular, that
$\ell \nmid \# W$. This implies, in particular, that  $\ell$ is a very good characteristic for
$\ell$ is a very good characteristic for  ${\widehat {G}}$.
${\widehat {G}}$.(ii) The subgroup
 $Z_{{\widehat {G}}^\text {ad}}(\overline {\sigma }_{\mathfrak m}(\Gamma _{K,|N|}))$ of
$Z_{{\widehat {G}}^\text {ad}}(\overline {\sigma }_{\mathfrak m}(\Gamma _{K,|N|}))$ of  ${\widehat {G}}_k$ is scheme-theoretically trivial.
${\widehat {G}}_k$ is scheme-theoretically trivial.(iii) The representation
 $\overline {\sigma }_{\mathfrak m}$ is absolutely
$\overline {\sigma }_{\mathfrak m}$ is absolutely  ${\widehat {G}}$-irreducible.
${\widehat {G}}$-irreducible.(iv) The subgroup
 $\overline {\sigma }_{\mathfrak m}(\Gamma _{K(\zeta _\ell ), |N|})$ of
$\overline {\sigma }_{\mathfrak m}(\Gamma _{K(\zeta _\ell ), |N|})$ of  ${\widehat {G}}(k)$ is
${\widehat {G}}(k)$ is  ${\widehat {G}}$-abundant.
${\widehat {G}}$-abundant.
In addition, we choose a global deformation problem ![]() ${\mathcal {D}} := (|N|, \{{\mathcal {D}}_v\}_{v \in |N|})$ for
${\mathcal {D}} := (|N|, \{{\mathcal {D}}_v\}_{v \in |N|})$ for ![]() ${\overline {\sigma }}_{\mathfrak {m}}$ such that all places of ramification for
${\overline {\sigma }}_{\mathfrak {m}}$ such that all places of ramification for ![]() ${\overline {\sigma }}_{\mathfrak {m}}$ are contained in
${\overline {\sigma }}_{\mathfrak {m}}$ are contained in ![]() $|N|$, and:
$|N|$, and:
(v) For each
 $v \in |N|$, the local deformation problem
$v \in |N|$, the local deformation problem  ${\mathcal {D}}_v$ is balanced in the sense of Definition 3.4 and unrestricted in the sense of Example 3.5. (So we require that
${\mathcal {D}}_v$ is balanced in the sense of Definition 3.4 and unrestricted in the sense of Example 3.5. (So we require that  $H^2(\Gamma _{K_v}, {\rm ad} \,\overline {\sigma }) = 0$ for
$H^2(\Gamma _{K_v}, {\rm ad} \,\overline {\sigma }) = 0$ for  $v \in |N|$.)
$v \in |N|$.)
Remark 4.4 Points (i), (ii), and (iv) are copied from [Reference Böckle, Harris, Khare and ThorneBHKT19, § 8.4], where their roles are explained. Point (iii) is a weakening of the ‘strongly ![]() ${\widehat {G}}$-irreducible’ condition of [Reference Böckle, Harris, Khare and ThorneBHKT19, § 8.4], which we are able to avoid here by appeal to the results of [Reference XueXue20b]. Point (v) allows us to invoke Proposition 3.9 to produce Taylor–Wiles primes for patching.
${\widehat {G}}$-irreducible’ condition of [Reference Böckle, Harris, Khare and ThorneBHKT19, § 8.4], which we are able to avoid here by appeal to the results of [Reference XueXue20b]. Point (v) allows us to invoke Proposition 3.9 to produce Taylor–Wiles primes for patching.
Let ![]() $R_{\overline {\sigma }_{\mathfrak m}, |N|, {\mathcal {D}}}$ be the corresponding global deformation ring (Proposition 3.6). From [Reference Böckle, Harris, Khare and ThorneBHKT19, Theorem 8.5] we have a pseudocharacter
$R_{\overline {\sigma }_{\mathfrak m}, |N|, {\mathcal {D}}}$ be the corresponding global deformation ring (Proposition 3.6). From [Reference Böckle, Harris, Khare and ThorneBHKT19, Theorem 8.5] we have a pseudocharacter ![]() $\Theta _{U(N)} = (\Theta _{U(N),n})_{n \geq 1}$ valued in
$\Theta _{U(N)} = (\Theta _{U(N),n})_{n \geq 1}$ valued in ![]() ${\mathcal {B}}(U(N), {\mathcal {O}})$, which factors through the quotient
${\mathcal {B}}(U(N), {\mathcal {O}})$, which factors through the quotient ![]() $\Gamma _K \to \Gamma _{K, |N|}$. Write
$\Gamma _K \to \Gamma _{K, |N|}$. Write ![]() $\Theta _{U(N), \mathfrak {m}}$ for the projection of the pseudocharacter
$\Theta _{U(N), \mathfrak {m}}$ for the projection of the pseudocharacter ![]() $\Theta _{U(N)}$ to
$\Theta _{U(N)}$ to ![]() ${\mathcal {B}}(U(N), {\mathcal {O}})_{\mathfrak {m}}$, and
${\mathcal {B}}(U(N), {\mathcal {O}})_{\mathfrak {m}}$, and ![]() $\sigma ^{\mathrm {univ}} \colon \Gamma _K \rightarrow \widehat {G}(R_{\overline {\sigma }_{\mathfrak m}, |N|, {\mathcal {D}}})$ for a representative of the universal deformation.
$\sigma ^{\mathrm {univ}} \colon \Gamma _K \rightarrow \widehat {G}(R_{\overline {\sigma }_{\mathfrak m}, |N|, {\mathcal {D}}})$ for a representative of the universal deformation.
The following lemma is a variant of [Reference Böckle, Harris, Khare and ThorneBHKT19, Lemma 8.19].
Lemma 4.5 There is a unique morphism ![]() $f_{\mathfrak m} : R_{\overline {\sigma }_{\mathfrak m}, |N|, {\mathcal {D}}} \to {\mathcal {B}}(U(N), {\mathcal {O}})_{\mathfrak m}$ of
$f_{\mathfrak m} : R_{\overline {\sigma }_{\mathfrak m}, |N|, {\mathcal {D}}} \to {\mathcal {B}}(U(N), {\mathcal {O}})_{\mathfrak m}$ of ![]() ${\mathcal {O}}$-algebras such that
${\mathcal {O}}$-algebras such that ![]() $f_{{\mathfrak m}, \ast } \operatorname {tr} \sigma ^{\mathrm {univ}} = \Theta _{U(N), {\mathfrak m}}$. It is surjective.
$f_{{\mathfrak m}, \ast } \operatorname {tr} \sigma ^{\mathrm {univ}} = \Theta _{U(N), {\mathfrak m}}$. It is surjective.
Proof. The existence and uniqueness of ![]() $f_{\mathfrak m}$ follow from [Reference Böckle, Harris, Khare and ThorneBHKT19, Theorem 4.10]. It is surjective because the ring
$f_{\mathfrak m}$ follow from [Reference Böckle, Harris, Khare and ThorneBHKT19, Theorem 4.10]. It is surjective because the ring ![]() ${\mathcal {B}}(U(N), {\mathcal {O}})_{\mathfrak m}$ is generated by the excursion operators
${\mathcal {B}}(U(N), {\mathcal {O}})_{\mathfrak m}$ is generated by the excursion operators ![]() $S_{I, (\gamma _i)_{i \in I}, f}$, each of which is explicitly realized as the image of the element
$S_{I, (\gamma _i)_{i \in I}, f}$, each of which is explicitly realized as the image of the element ![]() $f(\sigma ^{\mathrm {univ}}(\gamma _i)_{i \in I}) \in R_{\overline {\sigma }_{\mathfrak m}, |N|, {\mathcal {D}}}$.
$f(\sigma ^{\mathrm {univ}}(\gamma _i)_{i \in I}) \in R_{\overline {\sigma }_{\mathfrak m}, |N|, {\mathcal {D}}}$.
We can now prove the following generalization of [Reference Böckle, Harris, Khare and ThorneBHKT19, Theorem 8.20] that allows for ramification.
Theorem 4.6 Suppose ![]() $\mathfrak {m}$ satisfies assumptions (i)–(v) as above. Then
$\mathfrak {m}$ satisfies assumptions (i)–(v) as above. Then ![]() $C_{\mathrm {cusp}}(U(N), {\mathcal {O}})_{\mathfrak m}$ is a free
$C_{\mathrm {cusp}}(U(N), {\mathcal {O}})_{\mathfrak m}$ is a free ![]() $R_{\overline {\sigma }_{\mathfrak m}, |N|, {\mathcal {D}}}$-module,
$R_{\overline {\sigma }_{\mathfrak m}, |N|, {\mathcal {D}}}$-module, ![]() $f_{\mathfrak m}$ is an isomorphism, and
$f_{\mathfrak m}$ is an isomorphism, and ![]() $R_{\overline {\sigma }_{\mathfrak m}, |N|, {\mathcal {D}}}$ is a complete intersection
$R_{\overline {\sigma }_{\mathfrak m}, |N|, {\mathcal {D}}}$ is a complete intersection ![]() ${\mathcal {O}}$-algebra.
${\mathcal {O}}$-algebra.
Proof. The proof is an implementation of the Taylor–Wiles method. The argument runs similarly to [Reference Böckle, Harris, Khare and ThorneBHKT19, Theorem 8.20], but we give a summarized version with the necessary changes for our situation, and only sketching the parts which are the same.
Lemma 4.7 Let ![]() $U = \prod _v U_v$ be an open compact subgroup of
$U = \prod _v U_v$ be an open compact subgroup of ![]() $G(\widehat {{\mathcal {O}}}_K)$. Let
$G(\widehat {{\mathcal {O}}}_K)$. Let ![]() $V = \prod _v V_v \subset U$ be an open normal subgroup such that
$V = \prod _v V_v \subset U$ be an open normal subgroup such that ![]() $U/V$ is abelian of
$U/V$ is abelian of ![]() $\ell$-power order. Let
$\ell$-power order. Let ![]() $v_0$ be a place of
$v_0$ be a place of ![]() $K$, and let
$K$, and let ![]() $\ell ^M$ denote the order of an
$\ell ^M$ denote the order of an ![]() $\ell$-Sylow subgroup of
$\ell$-Sylow subgroup of ![]() $G(\mathbb {F}_{q_{v_0}}\!)$. Let
$G(\mathbb {F}_{q_{v_0}}\!)$. Let ![]() $V \leq W \leq U$ be a subgroup such that
$V \leq W \leq U$ be a subgroup such that ![]() $(U/V)[\ell ^M] \leq W / V$. Finally,
$(U/V)[\ell ^M] \leq W / V$. Finally, ![]() ${\mathfrak m} \subset {\mathcal {B}}(W, {\mathcal {O}})$ be a maximal ideal such that
${\mathfrak m} \subset {\mathcal {B}}(W, {\mathcal {O}})$ be a maximal ideal such that ![]() $\overline {\sigma }_{\mathfrak m}$ is absolutely
$\overline {\sigma }_{\mathfrak m}$ is absolutely ![]() ${\widehat {G}}$-irreducible. Then
${\widehat {G}}$-irreducible. Then ![]() $C_{\mathrm {cusp}}(W, {\mathcal {O}})_{\mathfrak m}$ is a finite free
$C_{\mathrm {cusp}}(W, {\mathcal {O}})_{\mathfrak m}$ is a finite free ![]() ${\mathcal {O}}[U/W]$-module.
${\mathcal {O}}[U/W]$-module.
Proof. In the case that ![]() $\overline {\sigma }_{\mathfrak m}$ is strongly
$\overline {\sigma }_{\mathfrak m}$ is strongly ![]() ${\widehat {G}}$-irreducible, this is exactly [Reference Böckle, Harris, Khare and ThorneBHKT19, Theorem 8.17]. Without this assumption, [Reference Böckle, Harris, Khare and ThorneBHKT19, Lemma 8.18] shows that
${\widehat {G}}$-irreducible, this is exactly [Reference Böckle, Harris, Khare and ThorneBHKT19, Theorem 8.17]. Without this assumption, [Reference Böckle, Harris, Khare and ThorneBHKT19, Lemma 8.18] shows that ![]() $C_c(W, {\mathcal {O}})$ is a free
$C_c(W, {\mathcal {O}})$ is a free ![]() ${\mathcal {O}}[U/W]$-module (though of infinite rank). Let
${\mathcal {O}}[U/W]$-module (though of infinite rank). Let ![]() $u$ be a place of
$u$ be a place of ![]() $K$ such that
$K$ such that ![]() $W_u = G({\mathcal {O}}_{K_u})$, and let
$W_u = G({\mathcal {O}}_{K_u})$, and let ![]() ${\mathcal {H}}_{G, u}$ denote the unramified Hecke algebra at
${\mathcal {H}}_{G, u}$ denote the unramified Hecke algebra at ![]() $u$ with
$u$ with ![]() ${\mathcal {O}}$-coefficients. Then
${\mathcal {O}}$-coefficients. Then ![]() $C_c(W, {\mathcal {O}})$ is a finite
$C_c(W, {\mathcal {O}})$ is a finite ![]() ${\mathcal {H}}_{G, u}$-module [Reference XueXue20b, Theorem 0.0.3]. According to [Reference XueXue20b, § 8], it is possible to define an
${\mathcal {H}}_{G, u}$-module [Reference XueXue20b, Theorem 0.0.3]. According to [Reference XueXue20b, § 8], it is possible to define an ![]() ${\mathcal {O}}$-subalgebra
${\mathcal {O}}$-subalgebra ![]() ${\mathcal {B}}_c(W, {\mathcal {O}}) \leq \operatorname {End}_{\mathcal {O}}(C_c(W, {\mathcal {O}}))$ of excursion operators, leaving invariant
${\mathcal {B}}_c(W, {\mathcal {O}}) \leq \operatorname {End}_{\mathcal {O}}(C_c(W, {\mathcal {O}}))$ of excursion operators, leaving invariant ![]() $C_{\mathrm {cusp}}(W, {\mathcal {O}})$, and extending
$C_{\mathrm {cusp}}(W, {\mathcal {O}})$, and extending ![]() ${\mathcal {B}}(W, {\mathcal {O}})$. Moreover, this ring contains the image of
${\mathcal {B}}(W, {\mathcal {O}})$. Moreover, this ring contains the image of ![]() ${\mathcal {H}}_{G, u}$ in
${\mathcal {H}}_{G, u}$ in ![]() $\operatorname {End}_{\mathcal {O}}(C_c(W, {\mathcal {O}}))$, showing that
$\operatorname {End}_{\mathcal {O}}(C_c(W, {\mathcal {O}}))$, showing that ![]() ${\mathcal {B}}_c(W, {\mathcal {O}})$ is a finite
${\mathcal {B}}_c(W, {\mathcal {O}})$ is a finite ![]() ${\mathcal {H}}_{G, u}$-algebra and that
${\mathcal {H}}_{G, u}$-algebra and that ![]() $C_c(W, {\mathcal {O}})$ is a finite
$C_c(W, {\mathcal {O}})$ is a finite ![]() ${\mathcal {B}}_c(W, {\mathcal {O}})$-module.
${\mathcal {B}}_c(W, {\mathcal {O}})$-module.
Let us identify ![]() ${\mathfrak m}$ with its pre-image in
${\mathfrak m}$ with its pre-image in ![]() ${\mathcal {B}}_c(W, {\mathcal {O}})$ under the canonical surjection
${\mathcal {B}}_c(W, {\mathcal {O}})$ under the canonical surjection ![]() ${\mathcal {B}}_c(W, {\mathcal {O}}) \to {\mathcal {B}}(W, {\mathcal {O}})$ (given by restricting excursion operators to
${\mathcal {B}}_c(W, {\mathcal {O}}) \to {\mathcal {B}}(W, {\mathcal {O}})$ (given by restricting excursion operators to ![]() $C_{\mathrm {cusp}}(W, {\mathcal {O}})$). To prove the lemma, it is enough to show that
$C_{\mathrm {cusp}}(W, {\mathcal {O}})$). To prove the lemma, it is enough to show that ![]() $C_{\mathrm {cusp}}(W, {\mathcal {O}})_{\mathfrak m}$ is a direct summand
$C_{\mathrm {cusp}}(W, {\mathcal {O}})_{\mathfrak m}$ is a direct summand ![]() ${\mathcal {B}}_c(W, {\mathcal {O}})$-submodule of the free
${\mathcal {B}}_c(W, {\mathcal {O}})$-submodule of the free ![]() ${\mathcal {O}}[U / W]$-module
${\mathcal {O}}[U / W]$-module ![]() $C_c(W, {\mathcal {O}})$. Using the constructions of [Reference XueXue20b], we see that there is a short exact sequence, respecting the action of excursion operators:
$C_c(W, {\mathcal {O}})$. Using the constructions of [Reference XueXue20b], we see that there is a short exact sequence, respecting the action of excursion operators:
 \[ 0 \to C_{\mathrm{cusp}}(W, {\mathcal{O}}) \to C_c(W, {\mathcal{O}}) \overset{\prod_{P \leq G} c_P}{\to} \prod_{P \leq G} C(U(\mathbb{A}_K) M(K) \backslash G(\mathbb{A}_K / W, {\mathcal{O}}), \]
\[ 0 \to C_{\mathrm{cusp}}(W, {\mathcal{O}}) \to C_c(W, {\mathcal{O}}) \overset{\prod_{P \leq G} c_P}{\to} \prod_{P \leq G} C(U(\mathbb{A}_K) M(K) \backslash G(\mathbb{A}_K / W, {\mathcal{O}}), \]
where the sum ranges over a set of representatives for the conjugacy classes of proper parabolic subgroups ![]() $P = M U$ of
$P = M U$ of ![]() $G$, and
$G$, and ![]() $c_P$ denotes the corresponding constant term morphism. Let
$c_P$ denotes the corresponding constant term morphism. Let ![]() $\mathscr {C}$ denote the image of
$\mathscr {C}$ denote the image of ![]() $C_c(W, {\mathcal {O}})$ under
$C_c(W, {\mathcal {O}})$ under ![]() $\prod _{P \leq G} c_P$, a
$\prod _{P \leq G} c_P$, a ![]() ${\mathcal {B}}_c(W, {\mathcal {O}})$-module. The proof will be complete if we can show that
${\mathcal {B}}_c(W, {\mathcal {O}})$-module. The proof will be complete if we can show that ![]() $\mathscr {C}_{\mathfrak m} = 0$. This follows from the absolute
$\mathscr {C}_{\mathfrak m} = 0$. This follows from the absolute ![]() ${\widehat {G}}$-irreducibility of
${\widehat {G}}$-irreducibility of ![]() $\overline {\sigma }_{\mathfrak m}$. Indeed, if
$\overline {\sigma }_{\mathfrak m}$. Indeed, if ![]() $\mathscr {C}_{\mathfrak m} \neq 0$, then the compatibility of excursion operators with constant term morphisms ([Reference XueXue20b, § 8.4]) shows, along exactly the same lines as in [Reference XueXue20a, § 4.2], that
$\mathscr {C}_{\mathfrak m} \neq 0$, then the compatibility of excursion operators with constant term morphisms ([Reference XueXue20b, § 8.4]) shows, along exactly the same lines as in [Reference XueXue20a, § 4.2], that ![]() $\overline {\sigma }_{\mathfrak m}$ must factor through
$\overline {\sigma }_{\mathfrak m}$ must factor through ![]() $\hat {M}(\overline {\mathbb {F}}_\ell )$ for some proper parabolic
$\hat {M}(\overline {\mathbb {F}}_\ell )$ for some proper parabolic ![]() $P = M U$ of
$P = M U$ of ![]() $G$. This is a contradiction to the absolute
$G$. This is a contradiction to the absolute ![]() ${\widehat {G}}$-irreducibility of
${\widehat {G}}$-irreducibility of ![]() $\overline {\sigma }_{\mathfrak m}$.
$\overline {\sigma }_{\mathfrak m}$.
We begin by preparing the usual setup for patching. Recall that we have fixed a choice ![]() $T \subset B \subset G$ of split maximal torus and Borel subgroup of
$T \subset B \subset G$ of split maximal torus and Borel subgroup of ![]() $G$. For a Taylor–Wiles datum
$G$. For a Taylor–Wiles datum ![]() $(Q, \{\varphi _v\}_{v \in Q})$, as in § 3.5, with
$(Q, \{\varphi _v\}_{v \in Q})$, as in § 3.5, with ![]() $Q$ disjoint from
$Q$ disjoint from ![]() $|N|$, we introduce the following notation. Extend the global deformation problem
$|N|$, we introduce the following notation. Extend the global deformation problem ![]() ${\mathcal {D}} = (|N|, \{{\mathcal {D}}_v\}_{v \in |N|})$ to
${\mathcal {D}} = (|N|, \{{\mathcal {D}}_v\}_{v \in |N|})$ to ![]() ${\mathcal {D}}_Q := (|N| \cup Q, \{{\mathcal {D}}_{Q,v}\}_{v\in |N| \cup Q})$ by setting
${\mathcal {D}}_Q := (|N| \cup Q, \{{\mathcal {D}}_{Q,v}\}_{v\in |N| \cup Q})$ by setting ![]() ${\mathcal {D}}_{Q, v} = {\mathcal {D}}_v$ if
${\mathcal {D}}_{Q, v} = {\mathcal {D}}_v$ if ![]() $v \in |N|$ and
$v \in |N|$ and ![]() ${\mathcal {D}}_{Q,v} = {\mathcal {D}}_{\overline {\sigma },v}^{\square }$ (the unrestricted deformation problem) if
${\mathcal {D}}_{Q,v} = {\mathcal {D}}_{\overline {\sigma },v}^{\square }$ (the unrestricted deformation problem) if ![]() $v \in Q$. Define
$v \in Q$. Define ![]() $\Delta _Q$ to be the maximal
$\Delta _Q$ to be the maximal ![]() $\ell$-power order quotient of the group
$\ell$-power order quotient of the group ![]() $\prod _{v \in Q} T(k(v))$. Using local class field theory, the action of the universal deformation ring for the restriction of
$\prod _{v \in Q} T(k(v))$. Using local class field theory, the action of the universal deformation ring for the restriction of ![]() $\overline {\sigma }_{\mathfrak m}$ to the tame inertia groups at places in
$\overline {\sigma }_{\mathfrak m}$ to the tame inertia groups at places in ![]() $Q$ equips
$Q$ equips ![]() $R_{\overline {\sigma }_{\mathfrak m}, |N| \cup Q, {\mathcal {D}}_Q}$ with a
$R_{\overline {\sigma }_{\mathfrak m}, |N| \cup Q, {\mathcal {D}}_Q}$ with a ![]() ${\mathcal {O}}[\Delta _Q]$-algebra structure. Writing
${\mathcal {O}}[\Delta _Q]$-algebra structure. Writing ![]() ${\mathfrak a}_Q \subset {\mathcal {O}}[\Delta _Q]$ for the augmentation ideal, we have a canonical isomorphism
${\mathfrak a}_Q \subset {\mathcal {O}}[\Delta _Q]$ for the augmentation ideal, we have a canonical isomorphism ![]() $R_{\overline {\sigma }_{\mathfrak m}, |N| \cup Q, {\mathcal {D}}_Q} / {\mathfrak a}_Q \cong R_{\overline {\sigma }_{\mathfrak m}, |N|, {\mathcal {D}}}$.
$R_{\overline {\sigma }_{\mathfrak m}, |N| \cup Q, {\mathcal {D}}_Q} / {\mathfrak a}_Q \cong R_{\overline {\sigma }_{\mathfrak m}, |N|, {\mathcal {D}}}$.
We now define the relevant level structures for patching. We define open compact subgroups ![]() $U_1(Q) \subset U_0(Q) \subset U(N)$ as follows:
$U_1(Q) \subset U_0(Q) \subset U(N)$ as follows:
•
 $U_0(Q) = \prod _v U_0(Q)_v$, where
$U_0(Q) = \prod _v U_0(Q)_v$, where  $U_0(Q)_v = U(N)_v = \ker ( G({\mathcal {O}}_{K_v}) \rightarrow G({\mathcal {O}}_{n_v \cdot v}))$ if
$U_0(Q)_v = U(N)_v = \ker ( G({\mathcal {O}}_{K_v}) \rightarrow G({\mathcal {O}}_{n_v \cdot v}))$ if  $v \not \in Q$, and
$v \not \in Q$, and  $U_0(Q)_v$ is an Iwahori group if
$U_0(Q)_v$ is an Iwahori group if  $v \in Q$;
$v \in Q$;•
 $U_1(Q) = \prod _v U_1(Q)_v$, where
$U_1(Q) = \prod _v U_1(Q)_v$, where  $U_1(Q)_v = U(N)_v$ if
$U_1(Q)_v = U(N)_v$ if  $v \not \in Q$, and
$v \not \in Q$, and  $U_1(Q)_v$ is the maximal pro-prime-to-
$U_1(Q)_v$ is the maximal pro-prime-to- $\ell$ subgroup of
$\ell$ subgroup of  $U_0(Q)_v$ if
$U_0(Q)_v$ if  $v \in Q$.
$v \in Q$.
Thus ![]() $U_1(Q) \triangleleft U_0(Q)$ is a normal subgroup, and there is a canonical isomorphism
$U_1(Q) \triangleleft U_0(Q)$ is a normal subgroup, and there is a canonical isomorphism ![]() $U_0 / U_1 \cong \Delta _Q$.
$U_0 / U_1 \cong \Delta _Q$.
We fix a place ![]() $v_0$ of
$v_0$ of ![]() $K$, and write
$K$, and write ![]() $\ell ^M$ for the order of the
$\ell ^M$ for the order of the ![]() $\ell$-Sylow subgroup of
$\ell$-Sylow subgroup of ![]() $G(\mathbb {F}_{q_{v_0}})$.
$G(\mathbb {F}_{q_{v_0}})$.
We now need to define auxiliary spaces of modular forms. We define ![]() $H'_0 = C_{\mathrm {cusp}}(U(N), {\mathcal {O}})_{\mathfrak m}$. There are surjective maps
$H'_0 = C_{\mathrm {cusp}}(U(N), {\mathcal {O}})_{\mathfrak m}$. There are surjective maps ![]() ${\mathcal {B}}(U_1(Q), {\mathcal {O}}) \twoheadrightarrow {\mathcal {B}}(U_0(Q), {\mathcal {O}}) \twoheadrightarrow {\mathcal {B}}(U(N), {\mathcal {O}})$, and we write
${\mathcal {B}}(U_1(Q), {\mathcal {O}}) \twoheadrightarrow {\mathcal {B}}(U_0(Q), {\mathcal {O}}) \twoheadrightarrow {\mathcal {B}}(U(N), {\mathcal {O}})$, and we write ![]() ${\mathfrak m}$ as well for the pullback of
${\mathfrak m}$ as well for the pullback of ![]() ${\mathfrak m} \subset {\mathcal {B}}(U(N), {\mathcal {O}})$ to these two algebras. As in Lemma 4.5, we have surjective morphisms
${\mathfrak m} \subset {\mathcal {B}}(U(N), {\mathcal {O}})$ to these two algebras. As in Lemma 4.5, we have surjective morphisms
We define ![]() $H'_{Q, 1} := C_{\mathrm {cusp}}(U_1(Q), {\mathcal {O}})_{\mathfrak m}$ and
$H'_{Q, 1} := C_{\mathrm {cusp}}(U_1(Q), {\mathcal {O}})_{\mathfrak m}$ and ![]() $H'_{Q, 0} := C_{\mathrm {cusp}}(U_0(Q), {\mathcal {O}})_{\mathfrak m}$.
$H'_{Q, 0} := C_{\mathrm {cusp}}(U_0(Q), {\mathcal {O}})_{\mathfrak m}$.
We discuss how to cut ![]() $H'_0$ out of
$H'_0$ out of ![]() $H'_{Q,0}$ as a direct summand, and an analogous construction for
$H'_{Q,0}$ as a direct summand, and an analogous construction for ![]() $H'_{Q,1}$. This will make use of the Hecke algebras
$H'_{Q,1}$. This will make use of the Hecke algebras ![]() ${\mathcal {H}}_{U_0(Q),v}$ at a place
${\mathcal {H}}_{U_0(Q),v}$ at a place ![]() $v \in Q$ (where it is the Iwahori–Hecke algebra by our choice of level structure) and
$v \in Q$ (where it is the Iwahori–Hecke algebra by our choice of level structure) and ![]() ${\mathcal {H}}_{U_1(Q),v}$. The ‘translation part’ of Bernstein's presentation of the Iwahori–Hecke algebra is an embedding
${\mathcal {H}}_{U_1(Q),v}$. The ‘translation part’ of Bernstein's presentation of the Iwahori–Hecke algebra is an embedding ![]() ${\mathcal {O}}[X_\ast (T)] \to {\mathcal {H}}_{U_0(Q)_v}$, whose action on
${\mathcal {O}}[X_\ast (T)] \to {\mathcal {H}}_{U_0(Q)_v}$, whose action on ![]() $H'_{Q,0}$ for
$H'_{Q,0}$ for ![]() $v \in Q$ induces an
$v \in Q$ induces an ![]() $R_{\overline {\sigma }_{\mathfrak m}, |N| \cup Q, {\mathcal {D}}_Q}[ \prod _{v \in Q} X_\ast (T) ]$-module structure on
$R_{\overline {\sigma }_{\mathfrak m}, |N| \cup Q, {\mathcal {D}}_Q}[ \prod _{v \in Q} X_\ast (T) ]$-module structure on ![]() $H'_{Q, 0}$. We write
$H'_{Q, 0}$. We write ![]() ${\mathfrak n}_{Q, 0} \subset {\mathcal {O}}[ \prod _{v \in Q} X_\ast (T) ]$ for the maximal ideal which is associated to the tuple of characters (
${\mathfrak n}_{Q, 0} \subset {\mathcal {O}}[ \prod _{v \in Q} X_\ast (T) ]$ for the maximal ideal which is associated to the tuple of characters (![]() $v \in Q$):
$v \in Q$):
Then ![]() $H'_{Q, 0, {\mathfrak n}_{Q, 0}}$ is a direct factor
$H'_{Q, 0, {\mathfrak n}_{Q, 0}}$ is a direct factor ![]() $R_{\overline {\sigma }_{\mathfrak m}, |N| \cup Q, {\mathcal {D}}_Q}$-module of
$R_{\overline {\sigma }_{\mathfrak m}, |N| \cup Q, {\mathcal {D}}_Q}$-module of ![]() $H'_{Q, 0}$, and there is a canonical isomorphism
$H'_{Q, 0}$, and there is a canonical isomorphism ![]() $H'_{Q, 0, {\mathfrak n}_{Q, 0}} \cong H'_0$ of
$H'_{Q, 0, {\mathfrak n}_{Q, 0}} \cong H'_0$ of ![]() $R_{\overline {\sigma }_{\mathfrak m}, |N| \cup Q, {\mathcal {D}}_Q}$-modules.Footnote 2
$R_{\overline {\sigma }_{\mathfrak m}, |N| \cup Q, {\mathcal {D}}_Q}$-modules.Footnote 2
Similarly, for ![]() $v \in Q$ we write
$v \in Q$ we write ![]() $T(K_v)_\ell$ for the quotient of
$T(K_v)_\ell$ for the quotient of ![]() $T(K_v)$ by its maximal pro-prime-to-
$T(K_v)$ by its maximal pro-prime-to-![]() $\ell$ subgroup. Then there is a structure of
$\ell$ subgroup. Then there is a structure of ![]() $R_{\overline {\sigma }_{\mathfrak m}, |N| \cup Q, {\mathcal {D}}_Q}[ \prod _{v \in Q} T(K_v)_\ell ]$-module on
$R_{\overline {\sigma }_{\mathfrak m}, |N| \cup Q, {\mathcal {D}}_Q}[ \prod _{v \in Q} T(K_v)_\ell ]$-module on ![]() $H'_{Q, 1}$, where the copy of
$H'_{Q, 1}$, where the copy of ![]() $T(K_v)_\ell$ corresponding to
$T(K_v)_\ell$ corresponding to ![]() $v \in Q$ acts via the analogous embedding
$v \in Q$ acts via the analogous embedding ![]() ${\mathcal {O}}[T(K_v)_\ell ] \to {\mathcal {H}}_{U_1(Q)_v}$. We write
${\mathcal {O}}[T(K_v)_\ell ] \to {\mathcal {H}}_{U_1(Q)_v}$. We write ![]() ${\mathfrak n}_{Q, 1} \subset {\mathcal {O}}[ \prod _{v \in Q} T(K_v)_\ell ]$ for the maximal ideal which is associated to the tuple of characters (4.2). Then
${\mathfrak n}_{Q, 1} \subset {\mathcal {O}}[ \prod _{v \in Q} T(K_v)_\ell ]$ for the maximal ideal which is associated to the tuple of characters (4.2). Then ![]() $H'_{Q, 1, {\mathfrak n}_{Q, 1}}$ is a direct factor
$H'_{Q, 1, {\mathfrak n}_{Q, 1}}$ is a direct factor ![]() $R_{\overline {\sigma }_{\mathfrak m}, |N| \cup Q, {\mathcal {D}}_Q}$-module of
$R_{\overline {\sigma }_{\mathfrak m}, |N| \cup Q, {\mathcal {D}}_Q}$-module of ![]() $H'_{Q, 1}$, and the two structures of
$H'_{Q, 1}$, and the two structures of ![]() ${\mathcal {O}}[\Delta _Q]$-module on
${\mathcal {O}}[\Delta _Q]$-module on ![]() $H'_{Q, 1, {\mathfrak n}_{Q, 1}}$, one arising from the homomorphism
$H'_{Q, 1, {\mathfrak n}_{Q, 1}}$, one arising from the homomorphism ![]() ${\mathcal {O}}[\Delta _Q] \to R_{\overline {\sigma }_{\mathfrak m}, |N| \cup Q, {\mathcal {D}}_Q}$ and the other from the homomorphism
${\mathcal {O}}[\Delta _Q] \to R_{\overline {\sigma }_{\mathfrak m}, |N| \cup Q, {\mathcal {D}}_Q}$ and the other from the homomorphism ![]() ${\mathcal {O}}[\Delta _Q] \to {\mathcal {O}}[\prod _{v \in Q} T(K_v)_\ell ]$, are the same.
${\mathcal {O}}[\Delta _Q] \to {\mathcal {O}}[\prod _{v \in Q} T(K_v)_\ell ]$, are the same.
We need two key properties of the modules ![]() $H'_{Q, 1}$ (with fixed
$H'_{Q, 1}$ (with fixed ![]() $j$ as in Proposition 3.9):
$j$ as in Proposition 3.9):
• The natural inclusion
induces an identification \[ C_{\mathrm{cusp}}(U_0(Q), {\mathcal{O}}) \subset C_{\mathrm{cusp}}(U_1(Q), {\mathcal{O}}) \]
\[ C_{\mathrm{cusp}}(U_0(Q), {\mathcal{O}}) \subset C_{\mathrm{cusp}}(U_1(Q), {\mathcal{O}}) \]
 $H'_{Q, 0, {\mathfrak n}_{Q, 0}} = (H'_{Q, 1, {\mathfrak n}_{Q, 1}})^{\Delta _Q}$.
$H'_{Q, 0, {\mathfrak n}_{Q, 0}} = (H'_{Q, 1, {\mathfrak n}_{Q, 1}})^{\Delta _Q}$.• By Lemma 4.7, we then have that if
 $q_v \equiv 1 \text { mod }\ell ^{M'}$ for each
$q_v \equiv 1 \text { mod }\ell ^{M'}$ for each  $v \in Q$ and for some
$v \in Q$ and for some  $M' \geq M$, then
$M' \geq M$, then  $(H'_{Q, 1})^{\ell ^{j} \Delta _Q}$ is a free
$(H'_{Q, 1})^{\ell ^{j} \Delta _Q}$ is a free  ${\mathcal {O}}[\Delta _Q / \ell ^{j} \Delta _Q]$-module for each
${\mathcal {O}}[\Delta _Q / \ell ^{j} \Delta _Q]$-module for each  $0 \leq j \leq M' - M$. This property implies in turn that
$0 \leq j \leq M' - M$. This property implies in turn that  $(H'_{Q, 1, {\mathfrak n}_{Q, 1}})^{\ell ^{j} \Delta _Q}$ is a free
$(H'_{Q, 1, {\mathfrak n}_{Q, 1}})^{\ell ^{j} \Delta _Q}$ is a free  ${\mathcal {O}}[\Delta _Q / \ell ^{j} \Delta _Q]$-module. Observe that
${\mathcal {O}}[\Delta _Q / \ell ^{j} \Delta _Q]$-module. Observe that  $\Delta _Q / \ell ^{j} \Delta _Q \cong ({\mathbb {Z}} / \ell ^{j} {\mathbb {Z}})^{\oplus r \# Q}$, where
$\Delta _Q / \ell ^{j} \Delta _Q \cong ({\mathbb {Z}} / \ell ^{j} {\mathbb {Z}})^{\oplus r \# Q}$, where  $r = \operatorname {rank} {\widehat {G}}$.
$r = \operatorname {rank} {\widehat {G}}$.
For patching it is a bit more convenient to work with the modules ![]() $H_Q := \operatorname {Hom}_{\mathcal {O}}((H'_{Q, 1, {\mathfrak n}_{Q, 1}})^{\ell ^{j} \Delta _Q}, {\mathcal {O}})$ and
$H_Q := \operatorname {Hom}_{\mathcal {O}}((H'_{Q, 1, {\mathfrak n}_{Q, 1}})^{\ell ^{j} \Delta _Q}, {\mathcal {O}})$ and ![]() $H_0 := \operatorname {Hom}_{\mathcal {O}}(H'_0, {\mathcal {O}})$. These are finite free
$H_0 := \operatorname {Hom}_{\mathcal {O}}(H'_0, {\mathcal {O}})$. These are finite free ![]() ${\mathcal {O}}$-modules, which we endow with their natural structures of
${\mathcal {O}}$-modules, which we endow with their natural structures of ![]() $R_{\overline {\sigma }_{\mathfrak m}, |N| \cup Q, {\mathcal {D}}_Q} \otimes _{{\mathcal {O}}[\Delta _Q]} {\mathcal {O}}[\Delta _Q / \ell ^{j} \Delta _Q]$-module and
$R_{\overline {\sigma }_{\mathfrak m}, |N| \cup Q, {\mathcal {D}}_Q} \otimes _{{\mathcal {O}}[\Delta _Q]} {\mathcal {O}}[\Delta _Q / \ell ^{j} \Delta _Q]$-module and ![]() $R_{\overline {\sigma }_{\mathfrak m}, |N|, {\mathcal {D}}_Q}$-module, respectively, by dualization. We can summarize the preceding discussion as follows:
$R_{\overline {\sigma }_{\mathfrak m}, |N|, {\mathcal {D}}_Q}$-module, respectively, by dualization. We can summarize the preceding discussion as follows:
• The module
 $H_Q$ is a finite free
$H_Q$ is a finite free  ${\mathcal {O}}[\Delta _Q / \ell ^{j} \Delta _Q]$-module, where
${\mathcal {O}}[\Delta _Q / \ell ^{j} \Delta _Q]$-module, where  ${\mathcal {O}}[\Delta _Q / \ell ^{j} \Delta _Q]$ acts via the algebra homomorphism
${\mathcal {O}}[\Delta _Q / \ell ^{j} \Delta _Q]$ acts via the algebra homomorphism
 \[ {\mathcal{O}}[\Delta_Q / \ell^{j} \Delta_Q] \to R_{\overline{\sigma}_{\mathfrak m}, |N| \cup Q, {\mathcal{D}}_Q} \otimes_{{\mathcal{O}}[\Delta_Q]} {\mathcal{O}}[\Delta_Q / \ell^{j} \Delta_Q]. \]
\[ {\mathcal{O}}[\Delta_Q / \ell^{j} \Delta_Q] \to R_{\overline{\sigma}_{\mathfrak m}, |N| \cup Q, {\mathcal{D}}_Q} \otimes_{{\mathcal{O}}[\Delta_Q]} {\mathcal{O}}[\Delta_Q / \ell^{j} \Delta_Q]. \]
• There is a natural surjective map
 $H_Q \twoheadrightarrow H_0$, which factors through an isomorphism
$H_Q \twoheadrightarrow H_0$, which factors through an isomorphism  $(H_Q)_{\Delta _Q} \xrightarrow {\sim } H_0$, and is compatible with the isomorphism
$(H_Q)_{\Delta _Q} \xrightarrow {\sim } H_0$, and is compatible with the isomorphism  $R_{\overline {\sigma }_{\mathfrak m}, |N| \cup Q, {\mathcal {D}}_Q} / {\mathfrak a}_Q \cong R_{\overline {\sigma }_{\mathfrak m}, |N|, {\mathcal {D}}}$.
$R_{\overline {\sigma }_{\mathfrak m}, |N| \cup Q, {\mathcal {D}}_Q} / {\mathfrak a}_Q \cong R_{\overline {\sigma }_{\mathfrak m}, |N|, {\mathcal {D}}}$.
Let ![]() $h := h^1_{{\mathcal {D}}}(\Gamma _{K, |N|}, {\rm ad} \,{\overline {\sigma }})$. By Proposition 3.9, we can find for each
$h := h^1_{{\mathcal {D}}}(\Gamma _{K, |N|}, {\rm ad} \,{\overline {\sigma }})$. By Proposition 3.9, we can find for each ![]() $j \geq 1$ a Taylor–Wiles datum
$j \geq 1$ a Taylor–Wiles datum ![]() $(Q_j, \{ \varphi _v \}_{v \in Q_j})$ which satisfies the following conditions:
$(Q_j, \{ \varphi _v \}_{v \in Q_j})$ which satisfies the following conditions:
•
 $Q_j$ is disjoint from
$Q_j$ is disjoint from  $|N|$.
$|N|$.• For each
 $v \in Q_N$, we have
$v \in Q_N$, we have  $q_v \equiv 1 \text { mod }\ell ^{j + M}$ and
$q_v \equiv 1 \text { mod }\ell ^{j + M}$ and  $\# Q_j= h$.
$\# Q_j= h$.• There exists a surjection
 ${\mathcal {O}}[[x_1, \ldots, x_g]]\twoheadrightarrow R_{\overline {\sigma }_{\mathfrak m}, |N| \cup Q_j, {\mathcal {D}}}$, where
${\mathcal {O}}[[x_1, \ldots, x_g]]\twoheadrightarrow R_{\overline {\sigma }_{\mathfrak m}, |N| \cup Q_j, {\mathcal {D}}}$, where  $g = hr$.
$g = hr$.
Define ![]() $R_\infty = {\mathcal {O}} \unicode{x27E6} X_1, \ldots, X_g \unicode{x27E7}$. The situation is summarized in the following diagram.
$R_\infty = {\mathcal {O}} \unicode{x27E6} X_1, \ldots, X_g \unicode{x27E7}$. The situation is summarized in the following diagram.

We now patch these objects together. This involves quotienting the objects in the diagram by open ideals to get diagrams of Artinian objects. Then because there are only finitely many isomorphism classes of such diagrams, one can pass to the inverse limit. The details of this process are the same as in [Reference Böckle, Harris, Khare and ThorneBHKT19, p. 48–49], so we skip to the conclusion. Define ![]() $\Delta _\infty := {\mathbb {Z}}_\ell ^g$,
$\Delta _\infty := {\mathbb {Z}}_\ell ^g$, ![]() $\Delta _j := \Delta _\infty / \ell ^{j}\Delta _\infty$,
$\Delta _j := \Delta _\infty / \ell ^{j}\Delta _\infty$, ![]() $S_\infty := {\mathcal {O}}\unicode{x27E6} \Delta _\infty \unicode{x27E7}$,
$S_\infty := {\mathcal {O}}\unicode{x27E6} \Delta _\infty \unicode{x27E7}$, ![]() ${\mathfrak b}_j := \ker (S_\infty \to {\mathcal {O}}[[\Delta _j]])$, and
${\mathfrak b}_j := \ker (S_\infty \to {\mathcal {O}}[[\Delta _j]])$, and ![]() ${\mathfrak b}_0 := \ker ( S_\infty \to {\mathcal {O}})$. By patching, we have the following objects:
${\mathfrak b}_0 := \ker ( S_\infty \to {\mathcal {O}})$. By patching, we have the following objects:
•
 $R^\infty$, a complete Noetherian local
$R^\infty$, a complete Noetherian local  ${\mathcal {O}}$-algebra with residue field
${\mathcal {O}}$-algebra with residue field  $k$, which is equipped with structures of
$k$, which is equipped with structures of  $S_\infty$-algebra and a surjective map
$S_\infty$-algebra and a surjective map  $R_\infty \twoheadrightarrow R^\infty$;
$R_\infty \twoheadrightarrow R^\infty$;•
 $H_\infty$, a finite
$H_\infty$, a finite  $R^\infty$-module;
$R^\infty$-module;•
 $\alpha _\infty$, an isomorphism
$\alpha _\infty$, an isomorphism  $R^\infty / {\mathfrak b}_0 \cong R_{\overline {\sigma }_{\mathfrak m}, |N|, {\mathcal {D}}}$;
$R^\infty / {\mathfrak b}_0 \cong R_{\overline {\sigma }_{\mathfrak m}, |N|, {\mathcal {D}}}$;•
 $\beta _\infty$, an isomorphism
$\beta _\infty$, an isomorphism  $H_\infty / {\mathfrak b}_0 \cong H_0$.
$H_\infty / {\mathfrak b}_0 \cong H_0$.
These objects have the following additional properties:
•
 $H_\infty$ is free as an
$H_\infty$ is free as an  $S_\infty$-module.
$S_\infty$-module.• The isomorphisms
 $\alpha _\infty$,
$\alpha _\infty$,  $\beta _\infty$ are compatible with the structure of
$\beta _\infty$ are compatible with the structure of  $R_{\overline {\sigma }_{\mathfrak m}, |N|, {\mathcal {D}}}$-module on
$R_{\overline {\sigma }_{\mathfrak m}, |N|, {\mathcal {D}}}$-module on  $H_0$.
$H_0$.
The situation is summarized in the following diagram.

Since ![]() $S_{\infty }$ is topologically free, we may choose the dashed arrow so that the leftmost triangle commutes.
$S_{\infty }$ is topologically free, we may choose the dashed arrow so that the leftmost triangle commutes.
We find that
and hence that these inequalities are equalities, ![]() $R_\infty \to R^\infty$ is an isomorphism, and (by the Auslander–Buchsbaum formula)
$R_\infty \to R^\infty$ is an isomorphism, and (by the Auslander–Buchsbaum formula) ![]() $H_\infty$ is also a free
$H_\infty$ is also a free ![]() $R^\infty$-module. It follows that
$R^\infty$-module. It follows that ![]() $H_\infty / {\mathfrak b}_0 \cong H_0$ is a free
$H_\infty / {\mathfrak b}_0 \cong H_0$ is a free ![]() $R^\infty / {\mathfrak b}_0 \cong R_{\overline {\sigma }_{\mathfrak m}, |N|, {\mathcal {D}}}$-module, and that
$R^\infty / {\mathfrak b}_0 \cong R_{\overline {\sigma }_{\mathfrak m}, |N|, {\mathcal {D}}}$-module, and that ![]() $R_{\overline {\sigma }_{\mathfrak m}, |N|, {\mathcal {D}}}$ is an
$R_{\overline {\sigma }_{\mathfrak m}, |N|, {\mathcal {D}}}$ is an ![]() ${\mathcal {O}}$-flat complete intersection. This in turn implies that
${\mathcal {O}}$-flat complete intersection. This in turn implies that ![]() $C_{\mathrm {cusp}}(U, {\mathcal {O}})_{\mathfrak m} \cong \operatorname {Hom}_{\mathcal {O}}(H_0, {\mathcal {O}})$ is a free
$C_{\mathrm {cusp}}(U, {\mathcal {O}})_{\mathfrak m} \cong \operatorname {Hom}_{\mathcal {O}}(H_0, {\mathcal {O}})$ is a free ![]() $R_{\overline {\sigma }_{\mathfrak m}, |N|, {\mathcal {D}}}$-module (since complete intersections are Gorenstein). This completes the proof of the theorem.
$R_{\overline {\sigma }_{\mathfrak m}, |N|, {\mathcal {D}}}$-module (since complete intersections are Gorenstein). This completes the proof of the theorem.
5. Formal smoothness of local deformations
This section is devoted to the proof of the following theorem, which guarantees that for all large enough ![]() $\ell$, the unrestricted local condition will be balanced at a place of ramification for any given cuspidal automorphic representation.
$\ell$, the unrestricted local condition will be balanced at a place of ramification for any given cuspidal automorphic representation.
Theorem 5.1 Let ![]() $\Pi \subset C_{\operatorname {cusp}}(G,\overline {{\mathbb {Q}}})$ be a cuspidal automorphic representation of
$\Pi \subset C_{\operatorname {cusp}}(G,\overline {{\mathbb {Q}}})$ be a cuspidal automorphic representation of ![]() $G({\mathbb {A}}_K\!)$ with coefficients in
$G({\mathbb {A}}_K\!)$ with coefficients in ![]() $\overline {{\mathbb {Q}}}$. For any prime number
$\overline {{\mathbb {Q}}}$. For any prime number ![]() $\ell \neq p$ let
$\ell \neq p$ let ![]() $\Pi _\ell = \Pi \otimes _{\overline {\mathbb {Q}}} \overline {{\mathbb {Q}}}_\ell$ denote its base change to
$\Pi _\ell = \Pi \otimes _{\overline {\mathbb {Q}}} \overline {{\mathbb {Q}}}_\ell$ denote its base change to ![]() $\overline {{\mathbb {Q}}}_\ell$. Suppose
$\overline {{\mathbb {Q}}}_\ell$. Suppose ![]() $\Pi$ is unramified outside the finite set
$\Pi$ is unramified outside the finite set ![]() $S$, and
$S$, and ![]() $\sigma _{\ell } \in \underline {\rho }_{\Pi, \ell }$ (notation as in Remark 4.2) has Zariski dense image. (As explained in Remark 4.2, this implies a posteriori that
$\sigma _{\ell } \in \underline {\rho }_{\Pi, \ell }$ (notation as in Remark 4.2) has Zariski dense image. (As explained in Remark 4.2, this implies a posteriori that ![]() $\sigma _{\Pi, \ell }$ exists, and then
$\sigma _{\Pi, \ell }$ exists, and then ![]() $\sigma _{\ell } = \sigma _{\Pi, \ell }$.) Then, letting
$\sigma _{\ell } = \sigma _{\Pi, \ell }$.) Then, letting
be a reduction of ![]() $\sigma _{\ell }$ mod
$\sigma _{\ell }$ mod ![]() $\ell$, there is an integer
$\ell$, there is an integer ![]() $c(\Pi )$, depending only on
$c(\Pi )$, depending only on ![]() $\Pi$, such that, for all
$\Pi$, such that, for all ![]() $v \in S$ and all
$v \in S$ and all ![]() $\ell > c(\Pi )$, we have
$\ell > c(\Pi )$, we have
We concurrently found two very different proofs of Theorem 5.1, and include them both below, as they both establish general results along the way that may be of independent interest. The proof in § 5.1 is based on a lifting theorem (Theorem 5.6) for global Galois representations, which is analogous to [Reference Barnet-Lamb, Gee, Geraghty and TaylorBGGT14, Theorem 4.3.1]; cf. also [Reference Khare and WintenbergerKW09, Corollary 4.7]. The lifting theorem implies that if ![]() $H^2({\Gamma _{K_v}}, {\rm ad}({\overline {\sigma }}_{\ell })) \neq 0$, then there is another lift of
$H^2({\Gamma _{K_v}}, {\rm ad}({\overline {\sigma }}_{\ell })) \neq 0$, then there is another lift of ![]() ${\overline {\sigma }}_{\ell }$ to characteristic
${\overline {\sigma }}_{\ell }$ to characteristic ![]() $0$ which is ‘less ramified’ at
$0$ which is ‘less ramified’ at ![]() $v$ than
$v$ than ![]() $\sigma _{\ell }$. By the global Langlands correspondence for
$\sigma _{\ell }$. By the global Langlands correspondence for ![]() $\operatorname {GL}_n$ established by Lafforgue [Reference LafforgueLaf02], such a lift must come from another cuspidal automorphic representation—of which only finitely many contribute at any given level structure—congruent to
$\operatorname {GL}_n$ established by Lafforgue [Reference LafforgueLaf02], such a lift must come from another cuspidal automorphic representation—of which only finitely many contribute at any given level structure—congruent to ![]() $\Pi$ modulo
$\Pi$ modulo ![]() $\ell$. The idea is then that there can only be finitely many such congruences, because otherwise strong multiplicity one for
$\ell$. The idea is then that there can only be finitely many such congruences, because otherwise strong multiplicity one for ![]() $\operatorname {GL}_n$ would be violated. We remark that a similar strategy, for an analogous situation over number fields, was used in the proof of [Reference GuiraudGui20, Corollary 7.11].
$\operatorname {GL}_n$ would be violated. We remark that a similar strategy, for an analogous situation over number fields, was used in the proof of [Reference GuiraudGui20, Corollary 7.11].
The proof in § 5.2 is of a more geometric nature. We reduce Theorem 5.1 to a torsion version of the weight-monodromy conjecture, formulated by Ito [Reference ItoIto21], for the compactifications constructed by Laurent Lafforgue to prove the global Langlands correspondence for ![]() $\operatorname {GL}_n$. Then we prove this torsion weight-monodromy conjecture for the intersection cohomology of any proper variety over an equal characteristic local field (generalizing work of Ito in the smooth proper case [Reference ItoIto21]). A crucial tool is an integral version of the decomposition theorem recently proved by Cadoret and Zheng, which we use to reduce to the smooth and proper case established by Ito. This second argument actually yields a more general statement, Theorem 5.9.
$\operatorname {GL}_n$. Then we prove this torsion weight-monodromy conjecture for the intersection cohomology of any proper variety over an equal characteristic local field (generalizing work of Ito in the smooth proper case [Reference ItoIto21]). A crucial tool is an integral version of the decomposition theorem recently proved by Cadoret and Zheng, which we use to reduce to the smooth and proper case established by Ito. This second argument actually yields a more general statement, Theorem 5.9.
Although neither argument gives an effective estimate on the constant ![]() $c(\Pi )$, they give different starting points for obtaining such an estimate. (That is one reason why it seems valuable to include both arguments.) In the first approach, what must be controlled is the set of primes at which cusp forms can have congruences to other cusp forms. In the second approach, what must be controlled has to do with the torsion in the integral intersection cohomology of L. Lafforgue's compactifications of moduli spaces of shtukas for
$c(\Pi )$, they give different starting points for obtaining such an estimate. (That is one reason why it seems valuable to include both arguments.) In the first approach, what must be controlled is the set of primes at which cusp forms can have congruences to other cusp forms. In the second approach, what must be controlled has to do with the torsion in the integral intersection cohomology of L. Lafforgue's compactifications of moduli spaces of shtukas for ![]() $\operatorname {GL}_n$.
$\operatorname {GL}_n$.
5.1 Approach based on lifting theorems for Galois representations
First we show that Theorem 5.1 follows from the same statement when ![]() $G = \operatorname {GL}_n$. Pick a faithful irreducible representation of
$G = \operatorname {GL}_n$. Pick a faithful irreducible representation of ![]() $G$ on a finite projective
$G$ on a finite projective ![]() $\mathbb {Z}$-module, say of rank
$\mathbb {Z}$-module, say of rank ![]() $n > 1$. This induces an injection
$n > 1$. This induces an injection ![]() $\mathfrak {g} \hookrightarrow \mathfrak {gl}_n$, which is split over
$\mathfrak {g} \hookrightarrow \mathfrak {gl}_n$, which is split over ![]() $\mathbb {Z}_{\ell }$ for all sufficiently large
$\mathbb {Z}_{\ell }$ for all sufficiently large ![]() $\ell$ and therefore induces an injection
$\ell$ and therefore induces an injection ![]() $H^2({\Gamma _{K_v}}, {\rm ad}({\overline {\sigma }}_{\ell })) \hookrightarrow H^2({\Gamma _{K_v}}, \mathfrak {gl}_n \circ {\overline {\sigma }}_{\ell })$. This reduces the claim to the case
$H^2({\Gamma _{K_v}}, {\rm ad}({\overline {\sigma }}_{\ell })) \hookrightarrow H^2({\Gamma _{K_v}}, \mathfrak {gl}_n \circ {\overline {\sigma }}_{\ell })$. This reduces the claim to the case ![]() $\widehat {G} = \operatorname {GL}_n$, so for the rest of this subsection we focus on the case
$\widehat {G} = \operatorname {GL}_n$, so for the rest of this subsection we focus on the case ![]() $G = \operatorname {GL}_n$.
$G = \operatorname {GL}_n$.
5.1.1 Some linear algebra
We recall the following result of Deligne [Reference DeligneDel80, Proposition 1.6.1].
Proposition 5.2 Let ![]() $k$ be a field and let
$k$ be a field and let ![]() $V$ be a finite-dimensional
$V$ be a finite-dimensional ![]() $k$-vector space, equipped with a nilpotent endomorphism
$k$-vector space, equipped with a nilpotent endomorphism ![]() $N : V \to V$. Then there exists a unique increasing filtration
$N : V \to V$. Then there exists a unique increasing filtration ![]() $M_\bullet$ of
$M_\bullet$ of ![]() $V$ such that
$V$ such that ![]() $N M_i \subset M_{i-2}$ and, for each
$N M_i \subset M_{i-2}$ and, for each ![]() $k \geq 0$,
$k \geq 0$, ![]() $N^k$ induces isomorphisms
$N^k$ induces isomorphisms ![]() $\operatorname {gr}_k M_\bullet \to \operatorname {gr}_{-k} M_\bullet$.
$\operatorname {gr}_k M_\bullet \to \operatorname {gr}_{-k} M_\bullet$.
If ![]() $N$ is a nilpotent endomorphism of an
$N$ is a nilpotent endomorphism of an ![]() $n$-dimensional vector space, we will write
$n$-dimensional vector space, we will write ![]() $\operatorname {Jord}(N)$ for the partition of
$\operatorname {Jord}(N)$ for the partition of ![]() $n$ given by the sizes of the Jordan blocks of
$n$ given by the sizes of the Jordan blocks of ![]() $N$. We recall that there is a partial order on partitions
$N$. We recall that there is a partial order on partitions ![]() $n$ which can be viewed as corresponding to the closure ordering of nilpotent orbits in the adjoint representation of
$n$ which can be viewed as corresponding to the closure ordering of nilpotent orbits in the adjoint representation of ![]() $\operatorname {GL}_n$.
$\operatorname {GL}_n$.
Let ![]() $v$ be a place of
$v$ be a place of ![]() $K$, and suppose given a prime
$K$, and suppose given a prime ![]() $\ell > n$ not dividing
$\ell > n$ not dividing ![]() $q$. Let
$q$. Let ![]() $E / {\mathbb {Q}}_\ell$ be a finite extension with residue field
$E / {\mathbb {Q}}_\ell$ be a finite extension with residue field ![]() $k_E = {\mathcal {O}}_E / (\varpi _E)$, and suppose given a continuous representation
$k_E = {\mathcal {O}}_E / (\varpi _E)$, and suppose given a continuous representation ![]() $\rho : G_{K_v} \to \operatorname {GL}_n({\mathcal {O}}_E)$. Fix a choice of (geometric) Frobenius lift
$\rho : G_{K_v} \to \operatorname {GL}_n({\mathcal {O}}_E)$. Fix a choice of (geometric) Frobenius lift ![]() $\phi _v \in G_{K_v}$, and
$\phi _v \in G_{K_v}$, and ![]() $t_\ell \in G_{K_v}$ a generator for the
$t_\ell \in G_{K_v}$ a generator for the ![]() $\ell$-part of tame inertia. Let us say that
$\ell$-part of tame inertia. Let us say that ![]() $\rho$ is good if the following conditions are satisfied:
$\rho$ is good if the following conditions are satisfied:
•
 $\rho$ is unipotently ramified. Let
$\rho$ is unipotently ramified. Let  $N = \log (\rho (t_\ell )) \in M_n({\mathcal {O}}_E)$; then
$N = \log (\rho (t_\ell )) \in M_n({\mathcal {O}}_E)$; then  $\phi _v N \phi _v^{-1} = q^{-1} N$.
$\phi _v N \phi _v^{-1} = q^{-1} N$.• The eigenvalues of
 $\rho (\phi _v)$ all lie in
$\rho (\phi _v)$ all lie in  $E$.
$E$.•
 $\rho$ is pure of weight 0. This means that the eigenvalues of
$\rho$ is pure of weight 0. This means that the eigenvalues of  $\rho (\phi _v)$ on
$\rho (\phi _v)$ on  $V = E^n$ are
$V = E^n$ are  $q_v$-Weil numbers and that, writing
$q_v$-Weil numbers and that, writing  $V_i \subset V$ for the subspace where the eigenvalues are of weight
$V_i \subset V$ for the subspace where the eigenvalues are of weight  $i$,
$i$,  $N^k$ induces an isomorphism
$N^k$ induces an isomorphism  $V_k \to V_{-k}$ for each
$V_k \to V_{-k}$ for each  $k \geq 0$. (Note that the filtration associated to
$k \geq 0$. (Note that the filtration associated to  $N$ by Proposition 5.2 is then
$N$ by Proposition 5.2 is then  $M_k = \bigoplus _{i \leq k} V_i$.)
$M_k = \bigoplus _{i \leq k} V_i$.)• Let
 $f_i(X) = \det (X - \rho (\phi _v)|_{V_i}) \in {\mathcal {O}}_E[X]$. Then for each
$f_i(X) = \det (X - \rho (\phi _v)|_{V_i}) \in {\mathcal {O}}_E[X]$. Then for each  $i \neq j$, the reduced polynomials
$i \neq j$, the reduced polynomials  $\overline {f}_i(X), \overline {f}_j(X) \in k_E[X]$ are coprime.
$\overline {f}_i(X), \overline {f}_j(X) \in k_E[X]$ are coprime.• For each
 $i, j$, the polynomials
$i, j$, the polynomials  $\overline {f}_i(X)$,
$\overline {f}_i(X)$,  $\overline {f}_j(q_v^{-1} X) \in k_E[X]$ fail to be coprime only if
$\overline {f}_j(q_v^{-1} X) \in k_E[X]$ fail to be coprime only if  $j = i + 2$.
$j = i + 2$.
Let ![]() $L = {\mathcal {O}}_E^n$, so that
$L = {\mathcal {O}}_E^n$, so that ![]() $V = L \otimes _{{\mathcal {O}}_E} E$, and define
$V = L \otimes _{{\mathcal {O}}_E} E$, and define ![]() $L_i = V_i \cap L$. Hensel's lemma implies that if
$L_i = V_i \cap L$. Hensel's lemma implies that if ![]() $\rho$ is good then
$\rho$ is good then ![]() $L = \bigoplus _{i \in {\mathbb {Z}}} L_i$.
$L = \bigoplus _{i \in {\mathbb {Z}}} L_i$.
Lemma 5.3 Suppose that ![]() $\rho$ is good, and let
$\rho$ is good, and let ![]() $\overline {N} \in M_n(k_E)$ denote the reduction of
$\overline {N} \in M_n(k_E)$ denote the reduction of ![]() $N$ modulo
$N$ modulo ![]() $\varpi _E$. If
$\varpi _E$. If ![]() $\operatorname {Jord}(\overline {N}) = \operatorname {Jord}(N)$, then
$\operatorname {Jord}(\overline {N}) = \operatorname {Jord}(N)$, then ![]() $H^2(K_v, {\rm ad} \,\overline {\rho }) = 0$.
$H^2(K_v, {\rm ad} \,\overline {\rho }) = 0$.
Proof. The equality ![]() $\operatorname {Jord}(\overline {N}) = \operatorname {Jord}(N)$ is equivalent to the equalities
$\operatorname {Jord}(\overline {N}) = \operatorname {Jord}(N)$ is equivalent to the equalities ![]() $\dim _E \ker N^k = \dim _{k_E} \ker \overline {N}^k$ for each
$\dim _E \ker N^k = \dim _{k_E} \ker \overline {N}^k$ for each ![]() $k \geq 0$. Let
$k \geq 0$. Let ![]() $\overline {L} = L \otimes _{{\mathcal {O}}_E} k_E$ and
$\overline {L} = L \otimes _{{\mathcal {O}}_E} k_E$ and ![]() $\overline {L}_i = L_i \otimes _{{\mathcal {O}}_E} k_E$. We first claim that for each
$\overline {L}_i = L_i \otimes _{{\mathcal {O}}_E} k_E$. We first claim that for each ![]() $k \geq 0$,
$k \geq 0$, ![]() $\overline {N}^k$ induces an isomorphism
$\overline {N}^k$ induces an isomorphism ![]() $\overline {L}_k \to \overline {L}_{-k}$. Equivalently, the intersection
$\overline {L}_k \to \overline {L}_{-k}$. Equivalently, the intersection ![]() $(\ker \overline {N}^k) \cap \overline {L}_k$ is 0.
$(\ker \overline {N}^k) \cap \overline {L}_k$ is 0.
The equality ![]() $\dim _E \ker N^k = \dim _{k_E} \ker \overline {N}^k$ implies that in fact
$\dim _E \ker N^k = \dim _{k_E} \ker \overline {N}^k$ implies that in fact ![]() $\ker \overline {N}^k = (\ker N^k \cap L) \otimes _{{\mathcal {O}}_E} k_E$. Since
$\ker \overline {N}^k = (\ker N^k \cap L) \otimes _{{\mathcal {O}}_E} k_E$. Since ![]() $\ker N^k$ is invariant under
$\ker N^k$ is invariant under ![]() $\operatorname {Ad} \rho (\phi _v)$, we find that in fact
$\operatorname {Ad} \rho (\phi _v)$, we find that in fact
This establishes the claim. By linear algebra, we then have a decomposition
 \[ \overline{L} = \bigoplus_{i \in {\mathbb{Z}}} \bigoplus_{j=0}^i \overline{N}^j \overline{L}(i), \]
\[ \overline{L} = \bigoplus_{i \in {\mathbb{Z}}} \bigoplus_{j=0}^i \overline{N}^j \overline{L}(i), \]
where ![]() $\overline {L}(i) = \overline {L}_i \cap (\ker \overline {N}^{i+1})$.
$\overline {L}(i) = \overline {L}_i \cap (\ker \overline {N}^{i+1})$.
By Tate duality, we need to show that ![]() $H^0(K_v, {\rm ad} \,\overline {\rho }(1)) = \operatorname {Hom}_{G_{K_v}}(\overline {L}, \overline {L}(1)) = 0$. An element of this Hom space determines a linear map
$H^0(K_v, {\rm ad} \,\overline {\rho }(1)) = \operatorname {Hom}_{G_{K_v}}(\overline {L}, \overline {L}(1)) = 0$. An element of this Hom space determines a linear map ![]() $F : \overline {L} \to \overline {L}$ which commutes with
$F : \overline {L} \to \overline {L}$ which commutes with ![]() $\overline {N}$ and satisfies
$\overline {N}$ and satisfies ![]() $F(\overline {L}_i) \subset \overline {L}_{i+2}$ for each
$F(\overline {L}_i) \subset \overline {L}_{i+2}$ for each ![]() $i \in {\mathbb {Z}}$. To show the Hom space vanishes, it is enough to show that
$i \in {\mathbb {Z}}$. To show the Hom space vanishes, it is enough to show that ![]() $F$ annihilates each
$F$ annihilates each ![]() $\overline {L}(i)$. However, if
$\overline {L}(i)$. However, if ![]() $x \in \overline {L}(i)$ then we find
$x \in \overline {L}(i)$ then we find ![]() $F(x) \in \overline {L}_{i+2}$ and
$F(x) \in \overline {L}_{i+2}$ and
The restriction of ![]() $\overline {N}^{i+1}$ to
$\overline {N}^{i+1}$ to ![]() $\overline {L}_{i+2}$ is injective, so this forces
$\overline {L}_{i+2}$ is injective, so this forces ![]() $F(x) = 0$, hence
$F(x) = 0$, hence ![]() $F = 0$, as required.
$F = 0$, as required.
5.1.2 Local lifting rings
Let ![]() $\ell > n$ be a prime not dividing
$\ell > n$ be a prime not dividing ![]() $q$ and let
$q$ and let ![]() $E / {\mathbb {Q}}_\ell$ be a finite extension with residue field
$E / {\mathbb {Q}}_\ell$ be a finite extension with residue field ![]() $k_E = {\mathcal {O}}_E / (\varpi _E)$. Let
$k_E = {\mathcal {O}}_E / (\varpi _E)$. Let ![]() $v$ be a place of
$v$ be a place of ![]() $K$ and fix a continuous homomorphism
$K$ and fix a continuous homomorphism ![]() $\overline {\rho }_v : G_{K_v} \to \operatorname {GL}_n(k_E)$ and a continuous character
$\overline {\rho }_v : G_{K_v} \to \operatorname {GL}_n(k_E)$ and a continuous character ![]() $\chi : G_K \to {\mathcal {O}}_E^\times$ such that
$\chi : G_K \to {\mathcal {O}}_E^\times$ such that ![]() $\det \overline {\rho }_v = \chi |_{G_{K_v}}$. Let
$\det \overline {\rho }_v = \chi |_{G_{K_v}}$. Let ![]() $\operatorname {CNL}_{{\mathcal {O}}_E}$ denote the category of complete Noetherian local
$\operatorname {CNL}_{{\mathcal {O}}_E}$ denote the category of complete Noetherian local ![]() ${\mathcal {O}}_E$-algebras with residue field
${\mathcal {O}}_E$-algebras with residue field ![]() $k_E$. Then the functor
$k_E$. Then the functor ![]() $L_v^\chi$ which associates to each
$L_v^\chi$ which associates to each ![]() $A \in \operatorname {CNL}_{{\mathcal {O}}_E}$ the set of lifts
$A \in \operatorname {CNL}_{{\mathcal {O}}_E}$ the set of lifts ![]() $\rho _{v, A} : G_{K_v} \to \operatorname {GL}_n(A)$ of
$\rho _{v, A} : G_{K_v} \to \operatorname {GL}_n(A)$ of ![]() $\overline {\rho }_v$ of determinant
$\overline {\rho }_v$ of determinant ![]() $\chi |_{G_{K_v}}$ is represented by an object
$\chi |_{G_{K_v}}$ is represented by an object ![]() $R_v^{\square, \chi } \in \operatorname {CNL}_{{\mathcal {O}}_E}$. This ring has a pleasant geometry.
$R_v^{\square, \chi } \in \operatorname {CNL}_{{\mathcal {O}}_E}$. This ring has a pleasant geometry.
Proposition 5.4 Let assumptions be as above. Then the following statements hold:
(i) The ring
 $R_v^{\square, \chi }$ is a reduced local complete intersection.
$R_v^{\square, \chi }$ is a reduced local complete intersection.(ii) For each minimal prime
 $\mathfrak {q} \subset R_v^{\square, \chi }$, the quotient
$\mathfrak {q} \subset R_v^{\square, \chi }$, the quotient  $R_v^{\square, \chi } / \mathfrak {q}$ is a domain of Krull dimension
$R_v^{\square, \chi } / \mathfrak {q}$ is a domain of Krull dimension  $n^2$.
$n^2$.(iii) Let
 $\mathfrak {q} \subset R_v^{\square, \chi }$ be a minimal prime, and let
$\mathfrak {q} \subset R_v^{\square, \chi }$ be a minimal prime, and let  $L_v^{\chi, \mathfrak {q}} \subset L_v^{\chi }$ be the corresponding subfunctor. Then
$L_v^{\chi, \mathfrak {q}} \subset L_v^{\chi }$ be the corresponding subfunctor. Then  $L_v^{\chi, \mathfrak {q}}$ is a local deformation problem, in the sense that for each
$L_v^{\chi, \mathfrak {q}}$ is a local deformation problem, in the sense that for each  $A \in \operatorname {CNL}_{{\mathcal {O}}_E}$, the subset
$A \in \operatorname {CNL}_{{\mathcal {O}}_E}$, the subset  $L_v^{\chi, \mathfrak {q}}(A) \subset L_v^\chi (A)$ is invariant under the conjugation action of the group
$L_v^{\chi, \mathfrak {q}}(A) \subset L_v^\chi (A)$ is invariant under the conjugation action of the group  $\ker (\operatorname {GL}_n(A) \to \operatorname {GL}_n(k_E))$.
$\ker (\operatorname {GL}_n(A) \to \operatorname {GL}_n(k_E))$.
Proof. The first two points follow from [Reference YaoYao, Proposition 2.13]. The third is established in [Reference Barnet-Lamb, Gee, Geraghty and TaylorBGGT14, § 1.3] in the case where the determinant is not fixed and ![]() $K_v$ is replaced by a finite extension of
$K_v$ is replaced by a finite extension of ![]() ${\mathbb {Q}}_p$ (
${\mathbb {Q}}_p$ (![]() $p \neq \ell$); the same proof applies here.
$p \neq \ell$); the same proof applies here.
We will use the following lemma.
Lemma 5.5 With assumptions as above, suppose further that ![]() $\ell > n$ and that
$\ell > n$ and that ![]() $\rho _v$ is unipotently ramified. Then there exists a minimal prime
$\rho _v$ is unipotently ramified. Then there exists a minimal prime ![]() $\mathfrak {q} \subset R_v^{\square, \chi }$ such that
$\mathfrak {q} \subset R_v^{\square, \chi }$ such that ![]() $R_v^{\square, \chi } / \mathfrak {q}$ is formally smooth over
$R_v^{\square, \chi } / \mathfrak {q}$ is formally smooth over ![]() ${\mathcal {O}}_E$ and such that for every homomorphism
${\mathcal {O}}_E$ and such that for every homomorphism ![]() $R_v^{\square, \chi } / \mathfrak {q} \to \overline {{\mathbb {Q}}}_\ell$, corresponding to a lifting
$R_v^{\square, \chi } / \mathfrak {q} \to \overline {{\mathbb {Q}}}_\ell$, corresponding to a lifting ![]() $\rho _v : G_{K_v} \to \operatorname {GL}_n(\overline {{\mathbb {Z}}}_\ell )$ of
$\rho _v : G_{K_v} \to \operatorname {GL}_n(\overline {{\mathbb {Z}}}_\ell )$ of ![]() $\overline {\rho }_v$ of determinant
$\overline {\rho }_v$ of determinant ![]() $\chi |_{G_{K_v}}$, the following conditions are satisfied:
$\chi |_{G_{K_v}}$, the following conditions are satisfied:
(i)
 $\rho _v$ is unipotently ramified.
$\rho _v$ is unipotently ramified.(ii) If
 $t_{\ell }\in I_{K_v}(\ell )$ denotes a generator of the
$t_{\ell }\in I_{K_v}(\ell )$ denotes a generator of the  $\ell$-part of tame inertia, then
$\ell$-part of tame inertia, then  $\operatorname {Jord}(\log (\rho _v(t_\ell ))) = \operatorname {Jord}(\log (\overline {\rho }_v(t_\ell )))$.
$\operatorname {Jord}(\log (\rho _v(t_\ell ))) = \operatorname {Jord}(\log (\overline {\rho }_v(t_\ell )))$.
Proof. We can take ![]() $R_v^{\square, \chi } / \mathfrak {q}$ to be the functor parametrizing liftings which are minimally ramified, in the sense of [Reference Clozel, Harris and TaylorCHT08, Definition 2.4.14], and of determinant
$R_v^{\square, \chi } / \mathfrak {q}$ to be the functor parametrizing liftings which are minimally ramified, in the sense of [Reference Clozel, Harris and TaylorCHT08, Definition 2.4.14], and of determinant ![]() $\chi |_{G_{K_v}}$. The claimed properties follow from [Reference Clozel, Harris and TaylorCHT08, Lemma 2.4.19].
$\chi |_{G_{K_v}}$. The claimed properties follow from [Reference Clozel, Harris and TaylorCHT08, Lemma 2.4.19].
5.1.3 Existence of lifts
Theorem 5.6 Let ![]() $\ell > n$ be a prime such that
$\ell > n$ be a prime such that ![]() $(\ell, 2q) = 1$, and let
$(\ell, 2q) = 1$, and let ![]() $\overline {\rho } : G_K \to \operatorname {GL}_n(\overline {{\mathbb {F}}}_\ell )$ be a continuous representation such that
$\overline {\rho } : G_K \to \operatorname {GL}_n(\overline {{\mathbb {F}}}_\ell )$ be a continuous representation such that ![]() $\overline {\rho }|_{G_{K \cdot \overline {{\mathbb {F}}}_q}}$ is irreducible. Let
$\overline {\rho }|_{G_{K \cdot \overline {{\mathbb {F}}}_q}}$ is irreducible. Let ![]() $S$ be a finite set of places of
$S$ be a finite set of places of ![]() $K$, containing the places at which
$K$, containing the places at which ![]() $\overline {\rho }$ is ramified, and fix the following data:
$\overline {\rho }$ is ramified, and fix the following data:
(i) a finite extension
 $E / {\mathbb {Q}}_\ell$ inside
$E / {\mathbb {Q}}_\ell$ inside  $\overline {{\mathbb {Q}}}_\ell$;
$\overline {{\mathbb {Q}}}_\ell$;(ii) a character
 $\chi : G_K \to {\mathcal {O}}_E^\times$ of finite order lifting
$\chi : G_K \to {\mathcal {O}}_E^\times$ of finite order lifting  $\det \overline {\rho }$, unramified outside
$\det \overline {\rho }$, unramified outside  $S$;
$S$;(iii) for each
 $v \in S$, a minimal prime
$v \in S$, a minimal prime  $\mathfrak {q}$ of the universal lifting ring
$\mathfrak {q}$ of the universal lifting ring  $R_v^{\square, \chi }$.
$R_v^{\square, \chi }$.
Then we can find a continuous lifting ![]() $\rho : G_K \to \operatorname {GL}_n(\overline {{\mathbb {Q}}}_\ell )$ of
$\rho : G_K \to \operatorname {GL}_n(\overline {{\mathbb {Q}}}_\ell )$ of ![]() $\overline {\rho }$ satisfying the following conditions:
$\overline {\rho }$ satisfying the following conditions:
(i)
 $\det \rho = \chi$.
$\det \rho = \chi$.(ii) For each place
 $v\not \in S$ of
$v\not \in S$ of  $K$,
$K$,  $\rho |_{G_{K_v}}$ is unramified.
$\rho |_{G_{K_v}}$ is unramified.(iii) For each place
 $v \in S$ of
$v \in S$ of  $K$,
$K$,  $\rho |_{G_{K_v}}$ defines a homomorphism
$\rho |_{G_{K_v}}$ defines a homomorphism  $R_v^{\square, \chi } / \mathfrak {q} \to \overline {{\mathbb {Q}}}_\ell$.
$R_v^{\square, \chi } / \mathfrak {q} \to \overline {{\mathbb {Q}}}_\ell$.
Proof. Let ![]() $D : \operatorname {CNL}_{{\mathcal {O}}_E} \to \operatorname {Sets}$ denote the functor of deformations
$D : \operatorname {CNL}_{{\mathcal {O}}_E} \to \operatorname {Sets}$ denote the functor of deformations ![]() $\rho _A : G_K \to \operatorname {GL}_n(A)$ of
$\rho _A : G_K \to \operatorname {GL}_n(A)$ of ![]() $\overline {\rho }$ satisfying the following conditions:
$\overline {\rho }$ satisfying the following conditions:
(i)
 $\det \rho _A = \chi$.
$\det \rho _A = \chi$.(ii) If
 $v \in S$, then
$v \in S$, then  $\rho _A|_{G_{K_v}}$ defines a map
$\rho _A|_{G_{K_v}}$ defines a map  $R_v^{\square, \chi } / \mathfrak {q} \to A$.
$R_v^{\square, \chi } / \mathfrak {q} \to A$.(iii) If
 $v \not \in S$, then
$v \not \in S$, then  $\rho _A|_{G_{K_v}}$ is unramified.
$\rho _A|_{G_{K_v}}$ is unramified.
Then ![]() $D$ is represented by an object
$D$ is represented by an object ![]() $R \in \operatorname {CNL}_{{\mathcal {O}}_E}$, and a standard computation in Galois cohomology and using Proposition 5.4 (see [Reference YaoYao, Corollary 5.4]) shows that
$R \in \operatorname {CNL}_{{\mathcal {O}}_E}$, and a standard computation in Galois cohomology and using Proposition 5.4 (see [Reference YaoYao, Corollary 5.4]) shows that ![]() $R$ has Krull dimension
$R$ has Krull dimension ![]() $\dim R \geq 1$. On the other hand,
$\dim R \geq 1$. On the other hand, ![]() $R$ is a finite
$R$ is a finite ![]() ${\mathcal {O}}_E$-algebra (see [Reference YaoYao, Theorem 5.5], where this is deduced from work of de Jong and Gaitsgory, [Reference de JongdeJ01, Reference GaitsgoryGai07]). It follows that
${\mathcal {O}}_E$-algebra (see [Reference YaoYao, Theorem 5.5], where this is deduced from work of de Jong and Gaitsgory, [Reference de JongdeJ01, Reference GaitsgoryGai07]). It follows that ![]() $R$ is an
$R$ is an ![]() ${\mathcal {O}}_E$-flat complete intersection and, in particular, that there exists a homomorphism
${\mathcal {O}}_E$-flat complete intersection and, in particular, that there exists a homomorphism ![]() $R \to \overline {{\mathbb {Q}}}_\ell$, which implies the existence of a lift
$R \to \overline {{\mathbb {Q}}}_\ell$, which implies the existence of a lift ![]() $\rho : G_K \to \operatorname {GL}_n(\overline {{\mathbb {Z}}}_\ell )$ with the desired properties.
$\rho : G_K \to \operatorname {GL}_n(\overline {{\mathbb {Z}}}_\ell )$ with the desired properties.
5.1.4 Minimality
Theorem 5.7 Let ![]() $\pi$ be a cuspidal automorphic representation of
$\pi$ be a cuspidal automorphic representation of ![]() $\operatorname {GL}_n(\mathbb {A}_K\!)$ over
$\operatorname {GL}_n(\mathbb {A}_K\!)$ over ![]() $\overline {{\mathbb {Q}}}$ of finite central character and such that the associated compatible system
$\overline {{\mathbb {Q}}}$ of finite central character and such that the associated compatible system ![]() $(r_\lambda (\pi ))_\lambda$ is connected, in the sense of [Reference Böckle, Gajda and PetersenBGP19]. Let
$(r_\lambda (\pi ))_\lambda$ is connected, in the sense of [Reference Böckle, Gajda and PetersenBGP19]. Let ![]() $S$ be a finite set of places of
$S$ be a finite set of places of ![]() $K$, including the set of places at which
$K$, including the set of places at which ![]() $\pi$ is ramified. Then there exists an integer
$\pi$ is ramified. Then there exists an integer ![]() $N > \max (2, q, n)$ such that for each prime number
$N > \max (2, q, n)$ such that for each prime number ![]() $\ell > N$ and for each place
$\ell > N$ and for each place ![]() $\lambda$ of
$\lambda$ of ![]() $\overline {{\mathbb {Q}}}$ of residue characteristic
$\overline {{\mathbb {Q}}}$ of residue characteristic ![]() $\ell$, the following conditions are satisfied:
$\ell$, the following conditions are satisfied:
(i)
 $\overline {\rho }_\lambda |_{G_{K \cdot \overline {{\mathbb {F}}}_q}}$ is irreducible.
$\overline {\rho }_\lambda |_{G_{K \cdot \overline {{\mathbb {F}}}_q}}$ is irreducible.(ii) For each
 $v \in S$,
$v \in S$,  $H^2(K_v, {\rm ad} \,\overline {\rho }_\lambda ) = 0$.
$H^2(K_v, {\rm ad} \,\overline {\rho }_\lambda ) = 0$.
Proof. Let ![]() $\chi$ denote the central character of
$\chi$ denote the central character of ![]() $\pi$, which we identify with a character
$\pi$, which we identify with a character ![]() $\chi : G_K \to \overline {{\mathbb {Q}}}^\times$. After replacing
$\chi : G_K \to \overline {{\mathbb {Q}}}^\times$. After replacing ![]() $K$ by a finite Galois extension, we may assume that for each place
$K$ by a finite Galois extension, we may assume that for each place ![]() $v \in S$,
$v \in S$, ![]() $\pi _v$ is unipotently ramified. We can associate to each
$\pi _v$ is unipotently ramified. We can associate to each ![]() $v \in S$ a partition
$v \in S$ a partition ![]() $\operatorname {Jord}(\pi _v)$ of
$\operatorname {Jord}(\pi _v)$ of ![]() $n$, namely the one given by the Jordan decomposition of the nilpotent part of the Weil–Deligne representation
$n$, namely the one given by the Jordan decomposition of the nilpotent part of the Weil–Deligne representation ![]() $\operatorname {{\rm rec}}_{K_v}(\pi _v)$.
$\operatorname {{\rm rec}}_{K_v}(\pi _v)$.
By [Reference Böckle, Gajda and PetersenBGP19, Corollary 6.12], we can find an integer ![]() $N_0 > \max (2, q, n)$ such that for each prime number
$N_0 > \max (2, q, n)$ such that for each prime number ![]() $\ell > N$ and for each place
$\ell > N$ and for each place ![]() $\lambda$ of
$\lambda$ of ![]() $\overline {{\mathbb {Q}}}$ of residue characteristic
$\overline {{\mathbb {Q}}}$ of residue characteristic ![]() $\ell$,
$\ell$, ![]() $\overline {\rho }_\lambda |_{G_{K \overline {{\mathbb {F}}}_q}}$ is irreducible. Since
$\overline {\rho }_\lambda |_{G_{K \overline {{\mathbb {F}}}_q}}$ is irreducible. Since ![]() $S$ is finite, it suffices to fix a single
$S$ is finite, it suffices to fix a single ![]() $w \in S$ and show that the number of primes
$w \in S$ and show that the number of primes ![]() $\ell > N_0$ such that there is a place
$\ell > N_0$ such that there is a place ![]() $\lambda | \ell$ of
$\lambda | \ell$ of ![]() $\overline {{\mathbb {Q}}}$ such that
$\overline {{\mathbb {Q}}}$ such that ![]() $H^2(K_w, {\rm ad} \,\overline {\rho }_\lambda ) \neq 0$ is finite.
$H^2(K_w, {\rm ad} \,\overline {\rho }_\lambda ) \neq 0$ is finite.
Let ![]() $L \subset \overline {{\mathbb {Q}}}$ be a number field such that the compatible system
$L \subset \overline {{\mathbb {Q}}}$ be a number field such that the compatible system ![]() $(r_\lambda (\pi ))_\lambda$ is
$(r_\lambda (\pi ))_\lambda$ is ![]() $L$-rational and such that the roots of
$L$-rational and such that the roots of ![]() $f(X) = \det (X - {\rm rec}_{K_w}(\pi _w)(\phi _w))$ lie in
$f(X) = \det (X - {\rm rec}_{K_w}(\pi _w)(\phi _w))$ lie in ![]() $L$. By the Ramanujan conjecture (established in [Reference LafforgueLaf02, Theorem VI.10]),
$L$. By the Ramanujan conjecture (established in [Reference LafforgueLaf02, Theorem VI.10]), ![]() ${\rm rec}_{K_w}(\pi _w)$ is pure of weight 0, and we may factor
${\rm rec}_{K_w}(\pi _w)$ is pure of weight 0, and we may factor ![]() $f(X) = \prod _i f_i(X)$, where the roots of
$f(X) = \prod _i f_i(X)$, where the roots of ![]() $f_i(X)$ are
$f_i(X)$ are ![]() $q_w$-Weil numbers of weight
$q_w$-Weil numbers of weight ![]() $i$. The polynomials
$i$. The polynomials ![]() $f(X)$,
$f(X)$, ![]() $f_i(X)$ lie in
$f_i(X)$ lie in ![]() ${\mathcal {O}}_L[1/q, X]$. If
${\mathcal {O}}_L[1/q, X]$. If ![]() $i \neq j$ then the polynomials
$i \neq j$ then the polynomials ![]() $f_i(X), f_j(X)$ are coprime. If
$f_i(X), f_j(X)$ are coprime. If ![]() $i \neq j+2$ then the polynomials
$i \neq j+2$ then the polynomials ![]() $f_i(X), f_{j+2}(q_w X)$ are coprime. After increasing
$f_i(X), f_{j+2}(q_w X)$ are coprime. After increasing ![]() $N_0$, we can therefore assume that for each prime
$N_0$, we can therefore assume that for each prime ![]() $\ell > N_0$ and for each place
$\ell > N_0$ and for each place ![]() $\lambda | \ell$ of
$\lambda | \ell$ of ![]() $\overline {{\mathbb {Q}}}$, the representation
$\overline {{\mathbb {Q}}}$, the representation ![]() $\rho _\lambda |_{G_{K_w}}$ (conjugated to take values in
$\rho _\lambda |_{G_{K_w}}$ (conjugated to take values in ![]() $\operatorname {GL}_n({\mathcal {O}}_E)$ for some
$\operatorname {GL}_n({\mathcal {O}}_E)$ for some ![]() $E / {\mathbb {Q}}_\ell$) is good, in the sense of § 5.1.1.
$E / {\mathbb {Q}}_\ell$) is good, in the sense of § 5.1.1.
Lemma 5.8 For each prime number ![]() $\ell > N_0$ and place
$\ell > N_0$ and place ![]() $\lambda | \ell$ of
$\lambda | \ell$ of ![]() $\overline {{\mathbb {Q}}}$ such that
$\overline {{\mathbb {Q}}}$ such that ![]() $H^2(K_w, {\rm ad} \,\overline {\rho }_\lambda ) \neq 0$, there exists a cuspidal automorphic representation
$H^2(K_w, {\rm ad} \,\overline {\rho }_\lambda ) \neq 0$, there exists a cuspidal automorphic representation ![]() $\pi '$ of
$\pi '$ of ![]() $\operatorname {GL}_n(\mathbb {A}_K)$ over
$\operatorname {GL}_n(\mathbb {A}_K)$ over ![]() $\overline {{\mathbb {Q}}}$ satisfying the following conditions:
$\overline {{\mathbb {Q}}}$ satisfying the following conditions:
(i)
 $\pi '$ has central character
$\pi '$ has central character  $\chi$ and is unramified outside
$\chi$ and is unramified outside  $S$.
$S$.(ii) For each place
 $v \in S$,
$v \in S$,  $\pi '_v$ is unipotently ramified.
$\pi '_v$ is unipotently ramified.(iii)
 $\operatorname {Jord}(\pi '_w) < \operatorname {Jord}(\pi _w)$.
$\operatorname {Jord}(\pi '_w) < \operatorname {Jord}(\pi _w)$.(iv) There is an isomorphism
 $\overline {r_\lambda (\pi )} \cong \overline {r_\lambda (\pi ')}$.
$\overline {r_\lambda (\pi )} \cong \overline {r_\lambda (\pi ')}$.
Proof. We would like to apply Theorem 5.6. We need to specify a minimal prime of each lifting ring ![]() $R_v^{\square, \chi }$ (
$R_v^{\square, \chi }$ (![]() $v \in S$). If
$v \in S$). If ![]() $v \neq w$ then we take any component containing the point corresponding to
$v \neq w$ then we take any component containing the point corresponding to ![]() $r_\lambda (\pi )$. If
$r_\lambda (\pi )$. If ![]() $v = w$ then we take the minimal lifting ring described in Lemma 5.5. We then apply Theorem 5.6 with these choices to obtain a lift
$v = w$ then we take the minimal lifting ring described in Lemma 5.5. We then apply Theorem 5.6 with these choices to obtain a lift ![]() $\rho$ of
$\rho$ of ![]() $\overline {r_\lambda (\pi )}$, which by the global Langlands correspondence for
$\overline {r_\lambda (\pi )}$, which by the global Langlands correspondence for ![]() $\operatorname {GL}_n(\mathbb {A}_K)$ corresponds to a cuspidal automorphic representation
$\operatorname {GL}_n(\mathbb {A}_K)$ corresponds to a cuspidal automorphic representation ![]() $\pi '$ of
$\pi '$ of ![]() $\operatorname {GL}_n(\mathbb {A}_K)$. The only property that remains to be justified is that
$\operatorname {GL}_n(\mathbb {A}_K)$. The only property that remains to be justified is that ![]() $\operatorname {Jord}(\pi '_w) < \operatorname {Jord}(\pi _w)$. By local–global compatibility, we have
$\operatorname {Jord}(\pi '_w) < \operatorname {Jord}(\pi _w)$. By local–global compatibility, we have ![]() $\operatorname {Jord}(\pi '_w) = \operatorname {Jord}(\rho |_{G_{K_w}}\!)$ (where we define the Jordan partition of a unipotently ramified representation to be that of the image of a generator of tame inertia). The definition of the minimally ramified deformation problem shows that
$\operatorname {Jord}(\pi '_w) = \operatorname {Jord}(\rho |_{G_{K_w}}\!)$ (where we define the Jordan partition of a unipotently ramified representation to be that of the image of a generator of tame inertia). The definition of the minimally ramified deformation problem shows that ![]() $\operatorname {Jord}(\rho |_{G_{K_w}}\!) = \operatorname {Jord}(\overline {r_\lambda (\pi )}|_{G_{K_w}}\!)$. Finally, Lemma 5.3 and our hypothesis that
$\operatorname {Jord}(\rho |_{G_{K_w}}\!) = \operatorname {Jord}(\overline {r_\lambda (\pi )}|_{G_{K_w}}\!)$. Finally, Lemma 5.3 and our hypothesis that ![]() $H^2(K_w, {\rm ad} \,\overline {\rho }_\lambda ) \neq 0$ show together that
$H^2(K_w, {\rm ad} \,\overline {\rho }_\lambda ) \neq 0$ show together that ![]() $\operatorname {Jord}(\overline {r_\lambda (\pi )}|_{G_{K_w}}\!) < \operatorname {Jord}(\pi _w)$.
$\operatorname {Jord}(\overline {r_\lambda (\pi )}|_{G_{K_w}}\!) < \operatorname {Jord}(\pi _w)$.
We now use the preceding lemma to finish the proof of the theorem. The set of cuspidal automorphic representations of ![]() $\operatorname {GL}_n(\mathbb {A}_K\!)$ over
$\operatorname {GL}_n(\mathbb {A}_K\!)$ over ![]() $\overline {{\mathbb {Q}}}$ of central character
$\overline {{\mathbb {Q}}}$ of central character ![]() $\chi$, unramified outside
$\chi$, unramified outside ![]() $S$, and unipotently ramified inside
$S$, and unipotently ramified inside ![]() $S$, is finite [Reference HarderHar74, Corollary 1.2.3]. Enlarge the number field
$S$, is finite [Reference HarderHar74, Corollary 1.2.3]. Enlarge the number field ![]() $L$ so that each such automorphic representation is in fact defined over
$L$ so that each such automorphic representation is in fact defined over ![]() $L$. If the number of places
$L$. If the number of places ![]() $\lambda$ of
$\lambda$ of ![]() $L$ for which
$L$ for which ![]() $H^2(K_w, {\rm ad} \,\overline {\rho }_\lambda ) \neq 0$ is infinite, then by the pigeonhole principle we can find an automorphic representation
$H^2(K_w, {\rm ad} \,\overline {\rho }_\lambda ) \neq 0$ is infinite, then by the pigeonhole principle we can find an automorphic representation ![]() $\pi '$ in this set such that for infinitely many places
$\pi '$ in this set such that for infinitely many places ![]() $\lambda$ of
$\lambda$ of ![]() $L$ there is an isomorphism
$L$ there is an isomorphism ![]() $\overline {r_\lambda (\pi )} \cong \overline {r_\lambda (\pi ')}$, and yet
$\overline {r_\lambda (\pi )} \cong \overline {r_\lambda (\pi ')}$, and yet ![]() $\operatorname {Jord}(\pi '_w) < \operatorname {Jord}(\pi _w)$. In particular,
$\operatorname {Jord}(\pi '_w) < \operatorname {Jord}(\pi _w)$. In particular, ![]() $\pi \neq \pi '$.
$\pi \neq \pi '$.
If ![]() $v \not \in S$ is a place of
$v \not \in S$ is a place of ![]() $K$ then, in particular, we find
$K$ then, in particular, we find ![]() $\det (X - r_\lambda (\pi )(\operatorname {Frob}_v)) \equiv \det (X - r_\lambda (\pi ')(\operatorname {Frob}_v)) \text { mod } \lambda$ for infinitely many places
$\det (X - r_\lambda (\pi )(\operatorname {Frob}_v)) \equiv \det (X - r_\lambda (\pi ')(\operatorname {Frob}_v)) \text { mod } \lambda$ for infinitely many places ![]() $\lambda$, and therefore
$\lambda$, and therefore ![]() $\pi _v \cong \pi '_v$. The strong multiplicity-one theorem then implies that
$\pi _v \cong \pi '_v$. The strong multiplicity-one theorem then implies that ![]() $\pi = \pi '$, contradicting the inequality
$\pi = \pi '$, contradicting the inequality ![]() $\operatorname {Jord}(\pi '_w) < \operatorname {Jord}(\pi _w)$. This concludes the proof.
$\operatorname {Jord}(\pi '_w) < \operatorname {Jord}(\pi _w)$. This concludes the proof.
5.2 Geometric approach based on the torsion weight-monodromy conjecture
We will actually establish the following more general statement, which handles arbitrary compatible systems of irreducible representations (as opposed to specifically the adjoint representation).
Theorem 5.9 Let ![]() $\{\sigma _{\ell } \colon \Gamma _{K,S} \rightarrow \operatorname {GL}_n(\overline {\mathbb {Q}}_{\ell })\}$ be any compatible system of irreducible
$\{\sigma _{\ell } \colon \Gamma _{K,S} \rightarrow \operatorname {GL}_n(\overline {\mathbb {Q}}_{\ell })\}$ be any compatible system of irreducible ![]() $n$-dimensional representations. For each
$n$-dimensional representations. For each ![]() $v \in |X|$, Grothendieck's quasi-unipotence theorem implies that there is an open subgroup
$v \in |X|$, Grothendieck's quasi-unipotence theorem implies that there is an open subgroup ![]() $J_v \subset I_{K_v}$ such that
$J_v \subset I_{K_v}$ such that ![]() $\sigma _{\ell }(J_v)$ is unipotent for all
$\sigma _{\ell }(J_v)$ is unipotent for all ![]() $\ell \neq p$. Choose for each
$\ell \neq p$. Choose for each ![]() $v \in |X|$ a
$v \in |X|$ a ![]() $t_v \in J_v$ projecting to a generator of the pro-
$t_v \in J_v$ projecting to a generator of the pro-![]() $\ell$ part of tame inertia for all but finitely many
$\ell$ part of tame inertia for all but finitely many ![]() $\ell \neq p$. Then all but finitely many primes
$\ell \neq p$. Then all but finitely many primes ![]() $\ell$ have the properties that:
$\ell$ have the properties that:
•
 ${\overline {\sigma }}_{\ell }$ is irreducible;
${\overline {\sigma }}_{\ell }$ is irreducible;• for all
 $v$,
$v$,  $\sigma _{\ell }(t_v) - 1$ has torsion-free cokernel on some (equivalently any) lattice.
$\sigma _{\ell }(t_v) - 1$ has torsion-free cokernel on some (equivalently any) lattice.
5.2.1 Some reductions
By assumption ![]() $G$ is semisimple; we may reduce to the case where
$G$ is semisimple; we may reduce to the case where ![]() $G$ is simple since the statement of the theorem is compatible with taking finite direct sums.
$G$ is simple since the statement of the theorem is compatible with taking finite direct sums.
The representation ![]() $\sigma _{\ell }$ is defined over a finite extension
$\sigma _{\ell }$ is defined over a finite extension ![]() $E/\mathbb {Q}_{\ell }$. Let
$E/\mathbb {Q}_{\ell }$. Let ![]() ${\mathcal {O}}_{E}$ be the ring of integers of
${\mathcal {O}}_{E}$ be the ring of integers of ![]() $E$, and
$E$, and ![]() $\widetilde {\sigma }_{\ell }$ be a lattice in
$\widetilde {\sigma }_{\ell }$ be a lattice in ![]() $\sigma _{\ell }$, with mod-
$\sigma _{\ell }$, with mod-![]() $\ell$ reduction
$\ell$ reduction ![]() ${\overline {\sigma }}_{\ell }$.
${\overline {\sigma }}_{\ell }$.
Lemma 5.10 If the cokernel of ![]() $(\widetilde {\sigma }_{\ell }(t_v)-1)^i$ is torsion-free for every
$(\widetilde {\sigma }_{\ell }(t_v)-1)^i$ is torsion-free for every ![]() $i$, then
$i$, then ![]() $H^2(K_v, {\overline {\sigma }}_{\ell }) = 0$.
$H^2(K_v, {\overline {\sigma }}_{\ell }) = 0$.
Proof. By [Reference ItoIto21, Lemma 3.7], the torsion-freeness implies that ![]() $\operatorname {Jord}(\widetilde {\sigma }_{\ell }(t_v)-1) = \operatorname {Jord} ({\overline {\sigma }}_{\ell }(t_v)-1)$ in the notation of Lemma 5.3, and then applying the same proof as for Lemma 5.3 gives the conclusion.
$\operatorname {Jord}(\widetilde {\sigma }_{\ell }(t_v)-1) = \operatorname {Jord} ({\overline {\sigma }}_{\ell }(t_v)-1)$ in the notation of Lemma 5.3, and then applying the same proof as for Lemma 5.3 gives the conclusion.
Lemma 5.11 Let ![]() $M$ be a finite flat
$M$ be a finite flat ![]() $\mathbb {Z}_{\ell }$-module and
$\mathbb {Z}_{\ell }$-module and ![]() $\gamma$ a
$\gamma$ a ![]() $\mathbb {Z}_{\ell }$-linear endomorphism of
$\mathbb {Z}_{\ell }$-linear endomorphism of ![]() $M$. If
$M$. If ![]() $(M \otimes _{\mathbb {Z}_{\ell }} M)_{\Delta \gamma }$ is torsion-free, then
$(M \otimes _{\mathbb {Z}_{\ell }} M)_{\Delta \gamma }$ is torsion-free, then ![]() $M_{\gamma }$ is torsion-free. (Here
$M_{\gamma }$ is torsion-free. (Here ![]() $\Delta \gamma$ refers to the diagonal action of
$\Delta \gamma$ refers to the diagonal action of ![]() $\gamma$ on the tensor product.)
$\gamma$ on the tensor product.)
Proof. Suppose ![]() $m \in M$ represents a non-zero
$m \in M$ represents a non-zero ![]() $\ell ^k$-torsion element of
$\ell ^k$-torsion element of ![]() $M_{\gamma }$. Then
$M_{\gamma }$. Then ![]() $m \otimes m \in M \otimes _{\mathbb {Z}_{\ell }} M$ represents an
$m \otimes m \in M \otimes _{\mathbb {Z}_{\ell }} M$ represents an ![]() $\ell ^{2k}$-torsion element of
$\ell ^{2k}$-torsion element of ![]() $(M \otimes _{\mathbb {Z}_{\ell }} M)_{\Delta \gamma }$. Furthermore, its image under
$(M \otimes _{\mathbb {Z}_{\ell }} M)_{\Delta \gamma }$. Furthermore, its image under ![]() $(M \otimes _{\mathbb {Z}_{\ell }} M)_{\Delta \gamma } \twoheadrightarrow M_{\gamma } \otimes _{\mathbb {Z}_{\ell }} M_{\Delta \gamma }$ is non-zero, so this shows that
$(M \otimes _{\mathbb {Z}_{\ell }} M)_{\Delta \gamma } \twoheadrightarrow M_{\gamma } \otimes _{\mathbb {Z}_{\ell }} M_{\Delta \gamma }$ is non-zero, so this shows that ![]() $(M \otimes _{\mathbb {Z}_{\ell }} M)_{\Delta \gamma }$ has a non-zero torsion element.
$(M \otimes _{\mathbb {Z}_{\ell }} M)_{\Delta \gamma }$ has a non-zero torsion element.
Hence it suffices to show that for all sufficiently large ![]() $\ell$, the cokernel of
$\ell$, the cokernel of ![]() $(\widetilde {\sigma }_{\ell }(t_v)-1)^i \otimes (\widetilde {\sigma }_{\ell }(t_v)-1)^i$ is torsion-free for all
$(\widetilde {\sigma }_{\ell }(t_v)-1)^i \otimes (\widetilde {\sigma }_{\ell }(t_v)-1)^i$ is torsion-free for all ![]() $i$. The point of casting the problem this way is that this tensor product of Galois representations appears in the cohomology of shtukas, and through this we will be able to transform the question into a purely geometric one.
$i$. The point of casting the problem this way is that this tensor product of Galois representations appears in the cohomology of shtukas, and through this we will be able to transform the question into a purely geometric one.
Let ![]() $n = \dim {\mathfrak g}$. Laurent Lafforgue constructed a proper Deligne–Mumford stack
$n = \dim {\mathfrak g}$. Laurent Lafforgue constructed a proper Deligne–Mumford stack
(our ![]() $\overline {\operatorname {Sht}}_N$ refers to what is called in [Reference LafforgueLaf02]
$\overline {\operatorname {Sht}}_N$ refers to what is called in [Reference LafforgueLaf02] ![]() $\overline {\mathrm {Cht}^{n, \overline {P} \leq P}_N}' / a^{\mathbb {Z}}$ for sufficiently large Harder–Narasimhan polygon
$\overline {\mathrm {Cht}^{n, \overline {P} \leq P}_N}' / a^{\mathbb {Z}}$ for sufficiently large Harder–Narasimhan polygon ![]() $P$, and appropriate
$P$, and appropriate ![]() $a$ corresponding to the central character of
$a$ corresponding to the central character of ![]() $\Pi$) such that (because
$\Pi$) such that (because ![]() $\sigma _{\ell }$ is irreducible)
$\sigma _{\ell }$ is irreducible) ![]() $\Xi \boxtimes (\sigma _{\ell } \otimes \sigma _{\ell })$ occurs, for someFootnote 3 Hecke module
$\Xi \boxtimes (\sigma _{\ell } \otimes \sigma _{\ell })$ occurs, for someFootnote 3 Hecke module ![]() $\Xi$, as a Hecke–Galois stable summand of
$\Xi$, as a Hecke–Galois stable summand of ![]() ${}^{\mathfrak {p}} H^0 (\overline {\operatorname {Sht}}_N, \operatorname {IC}(E))$ [Reference LafforgueLaf02, Theorem VI.27], where the latter refers to the zeroth perverse cohomology of the geometric generic fiber of
${}^{\mathfrak {p}} H^0 (\overline {\operatorname {Sht}}_N, \operatorname {IC}(E))$ [Reference LafforgueLaf02, Theorem VI.27], where the latter refers to the zeroth perverse cohomology of the geometric generic fiber of ![]() $\overline {\operatorname {Sht}}_N \rightarrow (X-N) \times (X-N)$.
$\overline {\operatorname {Sht}}_N \rightarrow (X-N) \times (X-N)$.
Corollary 5.12 For any ![]() $v \in |X|$, for all but finitely many
$v \in |X|$, for all but finitely many ![]() $\ell$, there exists
$\ell$, there exists ![]() $N$ disjoint from
$N$ disjoint from ![]() $v$ such that
$v$ such that ![]() $\widetilde {\sigma }_{\ell } \otimes _{{\mathcal {O}}_E} \widetilde {\sigma }_{\ell }$ occurs as a Hecke stableFootnote 4 summand of
$\widetilde {\sigma }_{\ell } \otimes _{{\mathcal {O}}_E} \widetilde {\sigma }_{\ell }$ occurs as a Hecke stableFootnote 4 summand of ![]() ${}^{\mathfrak {p}} H^0 (\overline {\operatorname {Sht}}_N, \operatorname {IC}({\mathcal {O}}_{E}))$ where
${}^{\mathfrak {p}} H^0 (\overline {\operatorname {Sht}}_N, \operatorname {IC}({\mathcal {O}}_{E}))$ where ![]() $\overline {\operatorname {Sht}}_N \rightarrow (X-N) \times (X-N)$ is a proper morphism of schemes.
$\overline {\operatorname {Sht}}_N \rightarrow (X-N) \times (X-N)$ is a proper morphism of schemes.
Proof. Fixing the Harder–Narasimhan polygon ![]() $p$, for all sufficiently large
$p$, for all sufficiently large ![]() $N$ [Reference VarshavskyVar04, Proposition 2.16] implies that the Deligne–Mumford stack
$N$ [Reference VarshavskyVar04, Proposition 2.16] implies that the Deligne–Mumford stack ![]() $\overline {\operatorname {Sht}}_N$ is represented by a scheme.
$\overline {\operatorname {Sht}}_N$ is represented by a scheme.
Since ![]() $\sigma _{\ell }$ is irreducible, the
$\sigma _{\ell }$ is irreducible, the ![]() $\sigma _{\ell }$-isotypic part of
$\sigma _{\ell }$-isotypic part of ![]() ${}^{\mathfrak {p}} H^0 (\overline {\operatorname {Sht}}_N, \operatorname {IC}(\overline {\mathbb {Q}}_{\ell }))$ occurs as a summand of the finite-dimensional subspace
${}^{\mathfrak {p}} H^0 (\overline {\operatorname {Sht}}_N, \operatorname {IC}(\overline {\mathbb {Q}}_{\ell }))$ occurs as a summand of the finite-dimensional subspace ![]() $H^*_{\mathrm {ess}}(\overline {\mathbb {Q}}_{\ell }) \subset {}^{\mathfrak {p}} H^0 (\overline {\operatorname {Sht}}_N, \operatorname {IC}(\overline {\mathbb {Q}}_{\ell }))$, where the ‘essential part’ is defined by the condition that its Hecke eigenvalues are cuspidal.
$H^*_{\mathrm {ess}}(\overline {\mathbb {Q}}_{\ell }) \subset {}^{\mathfrak {p}} H^0 (\overline {\operatorname {Sht}}_N, \operatorname {IC}(\overline {\mathbb {Q}}_{\ell }))$, where the ‘essential part’ is defined by the condition that its Hecke eigenvalues are cuspidal.
The Hecke operators act on ![]() $H^*_{\mathrm {ess}}(\overline {\mathbb {Q}}_{\ell })$, and the subalgebra of
$H^*_{\mathrm {ess}}(\overline {\mathbb {Q}}_{\ell })$, and the subalgebra of ![]() $\operatorname {End}(H^*_{\mathrm {ess}}(\overline {\mathbb {Q}}_{\ell }))$ generated by them forms a finite
$\operatorname {End}(H^*_{\mathrm {ess}}(\overline {\mathbb {Q}}_{\ell }))$ generated by them forms a finite ![]() $\overline {\mathbb {Q}}_{\ell }$-algebra, so we may choose a finite number of Hecke operators
$\overline {\mathbb {Q}}_{\ell }$-algebra, so we may choose a finite number of Hecke operators ![]() $T_1, \ldots, T_k$ that form a generating set. Each of these finitely many operators on
$T_1, \ldots, T_k$ that form a generating set. Each of these finitely many operators on ![]() $H^*_{N, \mathrm {ess}}$ satisfies a characteristic polynomial which is defined over a number field, hence for all sufficiently large
$H^*_{N, \mathrm {ess}}$ satisfies a characteristic polynomial which is defined over a number field, hence for all sufficiently large ![]() $\ell$ all their eigenvalues lie in
$\ell$ all their eigenvalues lie in ![]() $\overline {\mathbb {Z}}_{\ell }$. Since the projection to eigenspaces is given by universal polynomials in the eigenvalues, these projection operators are then defined over
$\overline {\mathbb {Z}}_{\ell }$. Since the projection to eigenspaces is given by universal polynomials in the eigenvalues, these projection operators are then defined over ![]() $\overline {\mathbb {Z}}_{\ell }$ for all sufficiently large
$\overline {\mathbb {Z}}_{\ell }$ for all sufficiently large ![]() $\ell$, giving a decomposition which then further descends to
$\ell$, giving a decomposition which then further descends to ![]() ${\mathcal {O}}_E$.
${\mathcal {O}}_E$.
For ![]() $\overline {\operatorname {Sht}}_N$ as in Corollary 5.12, by Grothendieck's quasi-unipotence theorem we may choose
$\overline {\operatorname {Sht}}_N$ as in Corollary 5.12, by Grothendieck's quasi-unipotence theorem we may choose ![]() $t_v$ to act unipotently on all of
$t_v$ to act unipotently on all of ![]() $H^0 ((\overline {\operatorname {Sht}}_N)_{K_v^{\rm s}}, \operatorname {IC}(\mathbb {Z}_{\ell }))$. It then suffices to show that for almost all
$H^0 ((\overline {\operatorname {Sht}}_N)_{K_v^{\rm s}}, \operatorname {IC}(\mathbb {Z}_{\ell }))$. It then suffices to show that for almost all ![]() $\ell$, the cokernel of
$\ell$, the cokernel of ![]() $(t_v-1)^i$ is torsion-free on
$(t_v-1)^i$ is torsion-free on ![]() $H^0 (\overline {\operatorname {Sht}}_N, \operatorname {IC}(\mathbb {Z}_{\ell }))$ for all
$H^0 (\overline {\operatorname {Sht}}_N, \operatorname {IC}(\mathbb {Z}_{\ell }))$ for all ![]() $i$. We will prove a much more general statement, for any smooth proper variety over
$i$. We will prove a much more general statement, for any smooth proper variety over ![]() $K_v$.
$K_v$.
5.2.2 Monodromy weight filtrations for torsion intersection cohomology
Let ![]() $Z$ be a proper variety over a characteristic-
$Z$ be a proper variety over a characteristic-![]() $p$ local field
$p$ local field ![]() $F$. Then we have an action of
$F$. Then we have an action of ![]() $\operatorname {Gal}(F^{\rm s}/F)$ on its (geometric) intersection cohomology
$\operatorname {Gal}(F^{\rm s}/F)$ on its (geometric) intersection cohomology ![]() $H^*(Z_{F^{\rm s}}, \operatorname {IC}_Z(\mathbb {Z}_{\ell }))$.
$H^*(Z_{F^{\rm s}}, \operatorname {IC}_Z(\mathbb {Z}_{\ell }))$.
There is an open subgroup ![]() $J \subset I_{F}$ such that its action is unipotent. Take
$J \subset I_{F}$ such that its action is unipotent. Take ![]() $t \in J$ such that its projection to the
$t \in J$ such that its projection to the ![]() $\ell$-part of tame inertia is non-trivial for all but finitely many
$\ell$-part of tame inertia is non-trivial for all but finitely many ![]() $\ell \neq p$.
$\ell \neq p$.
Proposition 5.13 For almost all ![]() $\ell \neq p$, the cokernel of
$\ell \neq p$, the cokernel of ![]() $(t-1)^i \colon H^*(Z_{F^{\rm s}}, \operatorname {IC}_Z(\mathbb {Z}_{\ell })) \rightarrow H^*(Z_{F^{\rm s}}, \operatorname {IC}_Z(\mathbb {Z}_{\ell }))$ is torsion-free for all
$(t-1)^i \colon H^*(Z_{F^{\rm s}}, \operatorname {IC}_Z(\mathbb {Z}_{\ell })) \rightarrow H^*(Z_{F^{\rm s}}, \operatorname {IC}_Z(\mathbb {Z}_{\ell }))$ is torsion-free for all ![]() $i$.
$i$.
In the special case where ![]() $Z$ is smooth and proper, this is a result of Ito [Reference ItoIto21], which ultimately relies on the weight-monodromy conjecture. Our proof will reduce to the smooth and proper case using the following proposition.
$Z$ is smooth and proper, this is a result of Ito [Reference ItoIto21], which ultimately relies on the weight-monodromy conjecture. Our proof will reduce to the smooth and proper case using the following proposition.
Proposition 5.14 Let ![]() $f \colon Y \rightarrow Z$ be an alteration of varieties over a field
$f \colon Y \rightarrow Z$ be an alteration of varieties over a field ![]() $L$, with
$L$, with ![]() $Y$ smooth over
$Y$ smooth over ![]() $L$. Then for all sufficiently large
$L$. Then for all sufficiently large ![]() $\ell$,
$\ell$, ![]() $Rf_* \mathbb {Z}_{\ell }$ has
$Rf_* \mathbb {Z}_{\ell }$ has ![]() $\operatorname {IC}_Z(\mathbb {Z}_{\ell })$ as a direct summand.
$\operatorname {IC}_Z(\mathbb {Z}_{\ell })$ as a direct summand.
Proof Proof of Proposition 5.13 assuming Proposition 5.14
According to de Jong [Reference de JongdeJ96], we may find an alteration ![]() $f \colon Y \rightarrow Z$ with
$f \colon Y \rightarrow Z$ with ![]() $Y$ being smooth and proper. The cokernels in question are then direct summands of the analogous cokernels for
$Y$ being smooth and proper. The cokernels in question are then direct summands of the analogous cokernels for ![]() $Y$, which by [Reference ItoIto21, combination of Lemma 3.7, Proposition 3.9, and Theorem 3.6] are torsion-free for all sufficiently large
$Y$, which by [Reference ItoIto21, combination of Lemma 3.7, Proposition 3.9, and Theorem 3.6] are torsion-free for all sufficiently large ![]() $\ell$.
$\ell$.
Remark 5.15 Our Proposition 5.14 also implies a torsion version of the weight-monodromy conjecture for the intersection cohomology of a proper variety ![]() $Z$ with
$Z$ with ![]() $\mathbb {F}_{\ell }$-coefficients, generalizing the case of smooth and proper
$\mathbb {F}_{\ell }$-coefficients, generalizing the case of smooth and proper ![]() $Z$ treated in [Reference ItoIto21].
$Z$ treated in [Reference ItoIto21].
The proof of Proposition 5.14 will be given at the end of this section. If we were considering ![]() $\mathbb {Q}_{\ell }$-coefficients instead, we would be able to deduce the analogous statement from the decomposition theorem (although it is not an entirely trivial deduction when
$\mathbb {Q}_{\ell }$-coefficients instead, we would be able to deduce the analogous statement from the decomposition theorem (although it is not an entirely trivial deduction when ![]() $F$ is not separably closed, since the splitting of the decomposition theorem over
$F$ is not separably closed, since the splitting of the decomposition theorem over ![]() $F^{\rm s}$ is not canonical, and does not descend to
$F^{\rm s}$ is not canonical, and does not descend to ![]() $F$ in general). For varieties over
$F$ in general). For varieties over ![]() $\mathbf {C}$, the statement with
$\mathbf {C}$, the statement with ![]() $\mathbb {Z}_{\ell }$-coefficients would follow for all sufficiently large
$\mathbb {Z}_{\ell }$-coefficients would follow for all sufficiently large ![]() $\ell$ from the
$\ell$ from the ![]() $\mathbb {Q}_{\ell }$-coefficient version plus the existence of a
$\mathbb {Q}_{\ell }$-coefficient version plus the existence of a ![]() $\mathbb {Z}$-structure on
$\mathbb {Z}$-structure on ![]() $Rf_* \mathbb {Z}_{\ell }$ and
$Rf_* \mathbb {Z}_{\ell }$ and ![]() $\operatorname {IC}(\mathbb {Z}_{\ell })$. However, Proposition 5.14 in the stated generality seemed out of reach until we learned of the recent theorem of Cadoret and Zheng, which gives a version of the decomposition theorem with
$\operatorname {IC}(\mathbb {Z}_{\ell })$. However, Proposition 5.14 in the stated generality seemed out of reach until we learned of the recent theorem of Cadoret and Zheng, which gives a version of the decomposition theorem with ![]() $\mathbb {Z}_{\ell }$-coefficients for all sufficiently large
$\mathbb {Z}_{\ell }$-coefficients for all sufficiently large ![]() $\ell$.
$\ell$.
Theorem 5.16 (Cadoret and Zheng [Reference Cadoret and ZhengCZ])
Let ![]() $f \colon Y \rightarrow Z$ be a proper surjection of finite type schemes over a field
$f \colon Y \rightarrow Z$ be a proper surjection of finite type schemes over a field ![]() $L$, with
$L$, with ![]() $Y$ is smooth over
$Y$ is smooth over ![]() $L$. Then for all sufficiently large
$L$. Then for all sufficiently large ![]() $\ell$, we have
$\ell$, we have
with each ![]() ${}^{\mathfrak {p}} {\mathcal {H}}^i (Rf_* \mathbb {Z}_{\ell })$ being torsion-free as a perverse sheaf.
${}^{\mathfrak {p}} {\mathcal {H}}^i (Rf_* \mathbb {Z}_{\ell })$ being torsion-free as a perverse sheaf.
Furthermore, if ![]() $L$ is separably closed, then for all sufficiently large
$L$ is separably closed, then for all sufficiently large ![]() $\ell$, each
$\ell$, each ![]() ${}^{\mathfrak {p}} {\mathcal {H}}^i (Rf_* \mathbb {Z}_{\ell })$ is isomorphic to a direct sum of intersection complexes of semisimple local systems.
${}^{\mathfrak {p}} {\mathcal {H}}^i (Rf_* \mathbb {Z}_{\ell })$ is isomorphic to a direct sum of intersection complexes of semisimple local systems.
5.2.3 Perverse sheaves
We would like to apply Theorem 5.16 to the situation of Proposition 5.14. A subtlety is that because the splitting provided by the decomposition theorem over ![]() $L^{\rm s}$ is not canonical, it does not in general descend to
$L^{\rm s}$ is not canonical, it does not in general descend to ![]() $L$. We must therefore pay careful attention to rationality issues. We will use a trick that we learned from Hansen's blogFootnote 5 (and which is credited there to Bhargav Bhatt, although we were later informed by Cadoret and Zheng that the argument essentially appears already around [Reference Beilinson, Bernstein and DeligneBBD82, § 5.3.11]) in order to deduce the necessary results.
$L$. We must therefore pay careful attention to rationality issues. We will use a trick that we learned from Hansen's blogFootnote 5 (and which is credited there to Bhargav Bhatt, although we were later informed by Cadoret and Zheng that the argument essentially appears already around [Reference Beilinson, Bernstein and DeligneBBD82, § 5.3.11]) in order to deduce the necessary results.
Definition 5.17 Let ![]() ${\mathcal {F}}$ be a perverse sheaf on a variety
${\mathcal {F}}$ be a perverse sheaf on a variety ![]() $Z$. Let
$Z$. Let ![]() $j \colon U \hookrightarrow Z$ be the inclusion of the maximal (dense) open variety on which
$j \colon U \hookrightarrow Z$ be the inclusion of the maximal (dense) open variety on which ![]() ${\mathcal {F}}$ is a (shifted) local system. We define the generic part of
${\mathcal {F}}$ is a (shifted) local system. We define the generic part of ![]() ${\mathcal {F}}$ to be the perverse sheaf
${\mathcal {F}}$ to be the perverse sheaf ![]() ${\mathcal {F}}^{\operatorname {gen}} := j_{!*} j^* {\mathcal {F}}$.
${\mathcal {F}}^{\operatorname {gen}} := j_{!*} j^* {\mathcal {F}}$.
We make no claim that there is a non-trivial map between ![]() ${\mathcal {F}}$ and
${\mathcal {F}}$ and ![]() ${\mathcal {F}}^{\operatorname {gen}}$ in general. However, we shall prove that in certain situations of interest,
${\mathcal {F}}^{\operatorname {gen}}$ in general. However, we shall prove that in certain situations of interest, ![]() ${\mathcal {F}}^{\operatorname {gen}}$ can be realized as a direct summand of
${\mathcal {F}}^{\operatorname {gen}}$ can be realized as a direct summand of ![]() ${\mathcal {F}}$.
${\mathcal {F}}$.
Proposition 5.18 Let ![]() ${\mathcal {F}}$ be a perverse sheaf on a variety
${\mathcal {F}}$ be a perverse sheaf on a variety ![]() $Z$ over
$Z$ over ![]() $L$. Suppose that
$L$. Suppose that ![]() ${\mathcal {F}}|_{Z_{L^{\rm s}}}$ is isomorphic to a direct sum of IC sheaves. Then
${\mathcal {F}}|_{Z_{L^{\rm s}}}$ is isomorphic to a direct sum of IC sheaves. Then ![]() ${\mathcal {F}}^{\operatorname {gen}}$ is a direct summand of
${\mathcal {F}}^{\operatorname {gen}}$ is a direct summand of ![]() ${\mathcal {F}}$.
${\mathcal {F}}$.
Proof. Let ![]() $j \colon U \rightarrow Z$ be as in Definition 5.17 and
$j \colon U \rightarrow Z$ be as in Definition 5.17 and ![]() $B$ be the closed complement of
$B$ be the closed complement of ![]() $U$. The hypothesis implies that
$U$. The hypothesis implies that ![]() ${\mathcal {F}}|_{Z_{L^{\rm s}}}$ is isomorphic to
${\mathcal {F}}|_{Z_{L^{\rm s}}}$ is isomorphic to ![]() ${\mathcal {F}}^{\operatorname {gen}}_{Z_{L^{\rm s}}} \oplus {\mathcal {E}}$ where
${\mathcal {F}}^{\operatorname {gen}}_{Z_{L^{\rm s}}} \oplus {\mathcal {E}}$ where ![]() ${\mathcal {E}}$ is a direct sum of IC sheaves supported on
${\mathcal {E}}$ is a direct sum of IC sheaves supported on ![]() $B_{L^{\rm s}}$.
$B_{L^{\rm s}}$.
Consider the maps ![]() $\alpha \colon ({}^{\mathfrak {p}} j_!) j^* {\mathcal {F}} \rightarrow {\mathcal {F}}$ and
$\alpha \colon ({}^{\mathfrak {p}} j_!) j^* {\mathcal {F}} \rightarrow {\mathcal {F}}$ and ![]() $\beta \colon {\mathcal {F}} \rightarrow ({}^{\mathfrak {p}} j_*) j^* {\mathcal {F}}$.
$\beta \colon {\mathcal {F}} \rightarrow ({}^{\mathfrak {p}} j_*) j^* {\mathcal {F}}$.
Let ![]() ${\mathcal {G}} := \operatorname {Im}(\alpha ) \subseteq {\mathcal {F}}$. Then we have a tautological map
${\mathcal {G}} := \operatorname {Im}(\alpha ) \subseteq {\mathcal {F}}$. Then we have a tautological map ![]() ${\mathcal {G}} \twoheadrightarrow {\mathcal {F}}^{\operatorname {gen}}$. Since
${\mathcal {G}} \twoheadrightarrow {\mathcal {F}}^{\operatorname {gen}}$. Since ![]() $({}^{\mathfrak {p}} j_! j^* {\mathcal {F}} )_{L^{\rm s}}$ has no proper quotients supported on
$({}^{\mathfrak {p}} j_! j^* {\mathcal {F}} )_{L^{\rm s}}$ has no proper quotients supported on ![]() $B_{L^{\rm s}}$ [Reference AcharAch21, Exercise 3.1.6], the composition
$B_{L^{\rm s}}$ [Reference AcharAch21, Exercise 3.1.6], the composition ![]() ${\mathcal {G}}_{L^{\rm s}} \rightarrow {\mathcal {F}}|_{Z_{L^{\rm s}}} \rightarrow {\mathcal {E}}$ vanishes, so that
${\mathcal {G}}_{L^{\rm s}} \rightarrow {\mathcal {F}}|_{Z_{L^{\rm s}}} \rightarrow {\mathcal {E}}$ vanishes, so that ![]() ${\mathcal {G}}_{L^{\rm s}} \hookrightarrow {\mathcal {F}}^{\operatorname {gen}}|_{L^{\rm s}}$. This implies that the given map
${\mathcal {G}}_{L^{\rm s}} \hookrightarrow {\mathcal {F}}^{\operatorname {gen}}|_{L^{\rm s}}$. This implies that the given map ![]() ${\mathcal {G}} \rightarrow {\mathcal {F}}^{\operatorname {gen}}$ is an isomorphism, which gives an injection
${\mathcal {G}} \rightarrow {\mathcal {F}}^{\operatorname {gen}}$ is an isomorphism, which gives an injection ![]() ${\mathcal {F}}^{\operatorname {gen}} \cong {\mathcal {G}} \hookrightarrow {\mathcal {F}}$. A dual argument shows that for
${\mathcal {F}}^{\operatorname {gen}} \cong {\mathcal {G}} \hookrightarrow {\mathcal {F}}$. A dual argument shows that for ![]() ${\mathcal {G}}' := \operatorname {Im}(\beta )$, we have a surjection
${\mathcal {G}}' := \operatorname {Im}(\beta )$, we have a surjection ![]() ${\mathcal {F}} \twoheadrightarrow {\mathcal {G}}' \cong {\mathcal {F}}^{\operatorname {gen}}$. We then check after base change to
${\mathcal {F}} \twoheadrightarrow {\mathcal {G}}' \cong {\mathcal {F}}^{\operatorname {gen}}$. We then check after base change to ![]() $L^{\rm s}$ that the composition
$L^{\rm s}$ that the composition ![]() ${\mathcal {F}}^{\operatorname {gen}} \hookrightarrow {\mathcal {F}} \twoheadrightarrow {\mathcal {F}}^{\operatorname {gen}}$ is the identity map.
${\mathcal {F}}^{\operatorname {gen}} \hookrightarrow {\mathcal {F}} \twoheadrightarrow {\mathcal {F}}^{\operatorname {gen}}$ is the identity map.
Corollary 5.19 Let ![]() $f \colon Y \rightarrow Z$ be a proper map of
$f \colon Y \rightarrow Z$ be a proper map of ![]() $L$-varieties, with
$L$-varieties, with ![]() $Y$ smooth over
$Y$ smooth over ![]() $L$. Then for all sufficiently large
$L$. Then for all sufficiently large ![]() $\ell$,
$\ell$, ![]() ${}^{\mathfrak {p}} {\mathcal {H}}^0 (Rf_* \operatorname {IC}_Y(\mathbb {Z}_{\ell }))^{\operatorname {gen}}$ is a direct summand of
${}^{\mathfrak {p}} {\mathcal {H}}^0 (Rf_* \operatorname {IC}_Y(\mathbb {Z}_{\ell }))^{\operatorname {gen}}$ is a direct summand of ![]() $Rf_* \operatorname {IC}_Y(\mathbb {Z}_{\ell })$.
$Rf_* \operatorname {IC}_Y(\mathbb {Z}_{\ell })$.
Proof. By Theorem 5.16, the hypothesis of Proposition 5.18 holds, so that ![]() ${}^{\mathfrak {p}} {\mathcal {H}}^0 (Rf_* \operatorname {IC}_Y(\mathbb {Z}_{\ell }))^{\operatorname {gen}}$ is a direct summand of
${}^{\mathfrak {p}} {\mathcal {H}}^0 (Rf_* \operatorname {IC}_Y(\mathbb {Z}_{\ell }))^{\operatorname {gen}}$ is a direct summand of ![]() ${}^{\mathfrak {p}} {\mathcal {H}}^0 (Rf_* \operatorname {IC}_Y(\mathbb {Z}_{\ell }))$. Applying Theorem 5.16 again,
${}^{\mathfrak {p}} {\mathcal {H}}^0 (Rf_* \operatorname {IC}_Y(\mathbb {Z}_{\ell }))$. Applying Theorem 5.16 again, ![]() ${}^{\mathfrak {p}} {\mathcal {H}}^0 (Rf_* \operatorname {IC}_Y(\mathbb {Z}_{\ell }))$ is a direct summand of
${}^{\mathfrak {p}} {\mathcal {H}}^0 (Rf_* \operatorname {IC}_Y(\mathbb {Z}_{\ell }))$ is a direct summand of ![]() $Rf_* \operatorname {IC}_Y(\mathbb {Z}_{\ell })$.
$Rf_* \operatorname {IC}_Y(\mathbb {Z}_{\ell })$.
Proof Proof of Proposition 5.14
By the definition of alteration, there is an open dense subset ![]() $U \subset Z$ over which the map
$U \subset Z$ over which the map ![]() $f|_U$ is finite flat. By shrinking
$f|_U$ is finite flat. By shrinking ![]() $U$ further if necessary, we may assume that
$U$ further if necessary, we may assume that ![]() $U$ is contained in the smooth locus of
$U$ is contained in the smooth locus of ![]() $Z$, so that
$Z$, so that ![]() $\operatorname {IC}_Z(\mathbb {Z}_{\ell })$ is the intermediate extension of
$\operatorname {IC}_Z(\mathbb {Z}_{\ell })$ is the intermediate extension of ![]() $\operatorname {IC}_Z(\mathbb {Z}_{\ell })|_U \cong \mathbb {Z}_{\ell }[\dim U]$. Over
$\operatorname {IC}_Z(\mathbb {Z}_{\ell })|_U \cong \mathbb {Z}_{\ell }[\dim U]$. Over ![]() $U$, the composition
$U$, the composition ![]() $\mathbb {Z}_{\ell } \rightarrow f_* \mathbb {Z}_{\ell } \xrightarrow {\operatorname {Tr}} \mathbb {Z}_{\ell }$ is multiplication by
$\mathbb {Z}_{\ell } \rightarrow f_* \mathbb {Z}_{\ell } \xrightarrow {\operatorname {Tr}} \mathbb {Z}_{\ell }$ is multiplication by ![]() $\deg f|_U$, hence as long as
$\deg f|_U$, hence as long as ![]() $\ell > \deg f|_U$ it realizes the constant sheaf
$\ell > \deg f|_U$ it realizes the constant sheaf ![]() $(\mathbb {Z}_{\ell })_U$ as a direct summand of
$(\mathbb {Z}_{\ell })_U$ as a direct summand of ![]() $f_* ((\mathbb {Z}_{\ell })_{f^{-1}(U)} ) \cong (Rf_* \mathbb {Z}_{\ell })|_U$. Since restriction to open subsets is perverse t-exact, this says that
$f_* ((\mathbb {Z}_{\ell })_{f^{-1}(U)} ) \cong (Rf_* \mathbb {Z}_{\ell })|_U$. Since restriction to open subsets is perverse t-exact, this says that ![]() $\operatorname {IC}_U(\mathbb {Z}_{\ell })$ is a summand of
$\operatorname {IC}_U(\mathbb {Z}_{\ell })$ is a summand of ![]() ${}^{\mathfrak {p}} {\mathcal {H}}^0(Rf_* \operatorname {IC}_Y(\mathbb {Z}_{\ell }))|_U$, and then applying intermediate extension shows that
${}^{\mathfrak {p}} {\mathcal {H}}^0(Rf_* \operatorname {IC}_Y(\mathbb {Z}_{\ell }))|_U$, and then applying intermediate extension shows that ![]() $\operatorname {IC}_Z(\mathbb {Z}_{\ell })$ is a direct summand of
$\operatorname {IC}_Z(\mathbb {Z}_{\ell })$ is a direct summand of ![]() ${}^{\mathfrak {p}} {\mathcal {H}}^0(Rf_* \operatorname {IC}_Y(\mathbb {Z}_{\ell }))^{\operatorname {gen}}$. We then conclude using Corollary 5.19.
${}^{\mathfrak {p}} {\mathcal {H}}^0(Rf_* \operatorname {IC}_Y(\mathbb {Z}_{\ell }))^{\operatorname {gen}}$. We then conclude using Corollary 5.19.
6. Global cyclic base change
6.1 Automorphic Galois representations
Let ![]() $R = \overline {\mathbb {F}}_{\ell }$ or
$R = \overline {\mathbb {F}}_{\ell }$ or ![]() $\overline {E}_{\lambda }$. In [Reference FengFen24, § 2], the abstract excursion algebra
$\overline {E}_{\lambda }$. In [Reference FengFen24, § 2], the abstract excursion algebra ![]() $\operatorname {Exc}(\Gamma _{K}, \widehat {G}_R)$ is defined. This is an algebra over
$\operatorname {Exc}(\Gamma _{K}, \widehat {G}_R)$ is defined. This is an algebra over ![]() $R$ such that the set of characters
$R$ such that the set of characters ![]() $\chi \colon \operatorname {Exc}(\Gamma _{K}, \widehat {G}_R) \rightarrow R$ is in bijection with semisimple (not necessarily continuous) representations
$\chi \colon \operatorname {Exc}(\Gamma _{K}, \widehat {G}_R) \rightarrow R$ is in bijection with semisimple (not necessarily continuous) representations ![]() $\sigma \in H^1( \Gamma _{K}, \widehat {G}(R))$. In [Reference XueXue20a, Reference XueXue20b], Cong Xue extends Lafforgue's methods to define an action of
$\sigma \in H^1( \Gamma _{K}, \widehat {G}(R))$. In [Reference XueXue20a, Reference XueXue20b], Cong Xue extends Lafforgue's methods to define an action of ![]() $\operatorname {Exc}(\Gamma _{K}, \widehat {G}_R)$ on
$\operatorname {Exc}(\Gamma _{K}, \widehat {G}_R)$ on ![]() $C_c^{\infty }(G(K) \setminus G(\mathbb {A}_K\!), R)$, preserving the cuspidal subspace. The same statement holds replacing
$C_c^{\infty }(G(K) \setminus G(\mathbb {A}_K\!), R)$, preserving the cuspidal subspace. The same statement holds replacing ![]() $\Gamma _{K}$ by
$\Gamma _{K}$ by ![]() $\Gamma _{K,N}$ and
$\Gamma _{K,N}$ and ![]() $G(K) \setminus G(\mathbb {A}_K\!)$ by
$G(K) \setminus G(\mathbb {A}_K\!)$ by ![]() $G(K) \setminus G(\mathbb {A}_K\!) / U(N)$. The algebra
$G(K) \setminus G(\mathbb {A}_K\!) / U(N)$. The algebra ![]() ${\mathcal {B}}(U(N),R)$ considered earlier in § 4.2 is the image of
${\mathcal {B}}(U(N),R)$ considered earlier in § 4.2 is the image of ![]() $\operatorname {Exc}(\Gamma _{K,N}, \widehat {G}_R)$ in
$\operatorname {Exc}(\Gamma _{K,N}, \widehat {G}_R)$ in ![]() $\operatorname {End}_R(C_{\operatorname {cusp}}(U(N), R))$.
$\operatorname {End}_R(C_{\operatorname {cusp}}(U(N), R))$.
Following [Reference FengFen24, Definition 5.5], we say that a Galois representation ![]() $\sigma \colon \Gamma _{K} \rightarrow \widehat {G}(R)$ is automorphic if the corresponding maximal ideal
$\sigma \colon \Gamma _{K} \rightarrow \widehat {G}(R)$ is automorphic if the corresponding maximal ideal ![]() $\mathfrak {m}_{\sigma }$ appears in the support of the
$\mathfrak {m}_{\sigma }$ appears in the support of the ![]() $\operatorname {Exc}(\Gamma _{K}, \widehat {G}_R)$-action on
$\operatorname {Exc}(\Gamma _{K}, \widehat {G}_R)$-action on ![]() $C_c(U(N), R)$ for some
$C_c(U(N), R)$ for some ![]() $N$. A priori this does not imply that
$N$. A priori this does not imply that ![]() $\sigma$ is related to a cusp form, but the following lemma shows that this is necessarily the case if
$\sigma$ is related to a cusp form, but the following lemma shows that this is necessarily the case if ![]() $\sigma$ is absolutely irreducible.
$\sigma$ is absolutely irreducible.
Lemma 6.1 Let ![]() $\sigma \colon \Gamma _{K, S} \rightarrow \widehat {G}(R)$ be an absolutely irreducible Galois representation which, moreover, is automorphic. Let
$\sigma \colon \Gamma _{K, S} \rightarrow \widehat {G}(R)$ be an absolutely irreducible Galois representation which, moreover, is automorphic. Let ![]() $\mathfrak {m}_{\sigma }$ the corresponding maximal ideal of
$\mathfrak {m}_{\sigma }$ the corresponding maximal ideal of ![]() $\operatorname {Exc}(\Gamma _K, \widehat {G}_R)$. If
$\operatorname {Exc}(\Gamma _K, \widehat {G}_R)$. If ![]() $\sigma$ is irreducible, then
$\sigma$ is irreducible, then ![]() $\mathfrak {m}_{\sigma }$ appears in the support of the
$\mathfrak {m}_{\sigma }$ appears in the support of the ![]() $\operatorname {Exc}(\Gamma _K, \widehat {G}_R)$-action on
$\operatorname {Exc}(\Gamma _K, \widehat {G}_R)$-action on ![]() $C_{\operatorname {cusp}}(U(N),R)$ for some
$C_{\operatorname {cusp}}(U(N),R)$ for some ![]() $N$, and for this
$N$, and for this ![]() $N$ there is an eigenvector
$N$ there is an eigenvector ![]() $f \in C_{\operatorname {cusp}}(U(N),R)$ on which
$f \in C_{\operatorname {cusp}}(U(N),R)$ on which ![]() ${\mathcal {B}}$ acts through the character
${\mathcal {B}}$ acts through the character ![]() ${\mathcal {B}}/\mathfrak {m}_{\sigma }$.
${\mathcal {B}}/\mathfrak {m}_{\sigma }$.
Proof. By [Reference XueXue20b, Proposition 7.6.2] and [Reference XueXue20a, § 6.2], for a parabolic subgroup ![]() $P \subset G$ with Levi
$P \subset G$ with Levi ![]() $M$, the constant term map
$M$, the constant term map
intertwines the action of ![]() $\operatorname {Exc}(\Gamma _{K}, \widehat {G}_R)$ on the source with the action of
$\operatorname {Exc}(\Gamma _{K}, \widehat {G}_R)$ on the source with the action of ![]() $\operatorname {Exc}(\Gamma _{K}, \widehat {M}_R)$ on the target, with respect to
$\operatorname {Exc}(\Gamma _{K}, \widehat {M}_R)$ on the target, with respect to ![]() $\widehat {M}(R) \hookrightarrow \widehat {G}(R)$. Therefore, all Galois representations attached by Lafforgue's construction to the image of
$\widehat {M}(R) \hookrightarrow \widehat {G}(R)$. Therefore, all Galois representations attached by Lafforgue's construction to the image of ![]() $\operatorname {CT}_G^P$ factor through
$\operatorname {CT}_G^P$ factor through ![]() $\widehat {M}(R)$. Hence if
$\widehat {M}(R)$. Hence if ![]() $\sigma$ does not factor through such a parabolic, and
$\sigma$ does not factor through such a parabolic, and ![]() $C_c(G,R)_{\mathfrak {m}_{\sigma }} \neq 0$, then we must have
$C_c(G,R)_{\mathfrak {m}_{\sigma }} \neq 0$, then we must have ![]() $C_{\operatorname {cusp}}(G,R)_{\mathfrak {m}_{\sigma }} \neq 0$.
$C_{\operatorname {cusp}}(G,R)_{\mathfrak {m}_{\sigma }} \neq 0$.
For the last statement, we note that since ![]() $C_{\operatorname {cusp}}(G,R) = \varinjlim _N C_{\operatorname {cusp}}(U,R)$, we have
$C_{\operatorname {cusp}}(G,R) = \varinjlim _N C_{\operatorname {cusp}}(U,R)$, we have ![]() $(C_{\operatorname {cusp}}(U,R))_{\mathfrak {m}_{\sigma }} \neq 0$ for some
$(C_{\operatorname {cusp}}(U,R))_{\mathfrak {m}_{\sigma }} \neq 0$ for some ![]() $U$. Since
$U$. Since ![]() $C_{\operatorname {cusp}}(U,R)$ is a finite-dimensional vector space over
$C_{\operatorname {cusp}}(U,R)$ is a finite-dimensional vector space over ![]() $R$, it is the direct sum of its generalized eigenspaces for the
$R$, it is the direct sum of its generalized eigenspaces for the ![]() $\operatorname {Exc}(\Gamma _{K}, \widehat {G}_R)$-action, and the assumption implies that the character
$\operatorname {Exc}(\Gamma _{K}, \widehat {G}_R)$-action, and the assumption implies that the character ![]() $\operatorname {Exc}(\Gamma _{K}, \widehat {G}_R) \rightarrow \operatorname {Exc}(\Gamma _{K}, \widehat {G}_R) / \mathfrak {m}_{\sigma }$ appears among the systems of eigenvalues.
$\operatorname {Exc}(\Gamma _{K}, \widehat {G}_R) \rightarrow \operatorname {Exc}(\Gamma _{K}, \widehat {G}_R) / \mathfrak {m}_{\sigma }$ appears among the systems of eigenvalues.
6.2 Mod  $\ell$ base change
$\ell$ base change
We suppose ![]() $\ell$ is odd and is a good prime for the reductive group
$\ell$ is odd and is a good prime for the reductive group ![]() $G$. Explicitly, this means that we require
$G$. Explicitly, this means that we require ![]() $p>2$ if
$p>2$ if ![]() $\widehat {G}$ has simple factors of type
$\widehat {G}$ has simple factors of type ![]() $A,B,C$ or
$A,B,C$ or ![]() $D$;
$D$; ![]() $p>3$ if
$p>3$ if ![]() $\widehat {G}$ has simple factors of type
$\widehat {G}$ has simple factors of type ![]() $G_2, F_4, E_6, E_7$; and
$G_2, F_4, E_6, E_7$; and ![]() $p>5$ if
$p>5$ if ![]() $\widehat {G}$ has simple factors of type
$\widehat {G}$ has simple factors of type ![]() $E_8$. Let
$E_8$. Let ![]() $K'/K$ be a cyclic extension of function fields of degree
$K'/K$ be a cyclic extension of function fields of degree ![]() $\ell$.
$\ell$.
Theorem 6.2 [Reference FengFen24, Theorem 1.6]
With notation as above, let ![]() ${\overline {\sigma }}: \Gamma _{K} \rightarrow {\widehat {G}}(\overline {{\mathbb {F}}}_\ell )$ be an automorphic Galois representation. Then the restriction
${\overline {\sigma }}: \Gamma _{K} \rightarrow {\widehat {G}}(\overline {{\mathbb {F}}}_\ell )$ be an automorphic Galois representation. Then the restriction ![]() ${\overline {\sigma }}|_{\Gamma _{K'}}$ is automorphic for
${\overline {\sigma }}|_{\Gamma _{K'}}$ is automorphic for ![]() $G_{K'}$.
$G_{K'}$.
6.3 Existence of almost all cyclic base changes in characteristic 0
Theorem 6.3 Let ![]() $\Pi$ be a cuspidal automorphic representation of
$\Pi$ be a cuspidal automorphic representation of ![]() $G({\mathbb {A}}_K)$ defined over a number field
$G({\mathbb {A}}_K)$ defined over a number field ![]() $E$.Footnote 6 Suppose the Mumford–Tate group of
$E$.Footnote 6 Suppose the Mumford–Tate group of ![]() $\Pi$ is
$\Pi$ is ![]() ${\widehat {G}}$, as in Definition 4.3. For a place
${\widehat {G}}$, as in Definition 4.3. For a place ![]() $\lambda$ of
$\lambda$ of ![]() $E$, let
$E$, let ![]() $\sigma _{\Pi,\lambda }$ be Lafforgue's parameter attached to
$\sigma _{\Pi,\lambda }$ be Lafforgue's parameter attached to ![]() $\Pi$ (as noted in Remark 4.2, the hypothesis implies that
$\Pi$ (as noted in Remark 4.2, the hypothesis implies that ![]() $\underline {\rho }_{\Pi, \lambda }$ is a singleton, so that
$\underline {\rho }_{\Pi, \lambda }$ is a singleton, so that ![]() $\sigma _{\Pi, \lambda }$ exists).
$\sigma _{\Pi, \lambda }$ exists).
Then there is an integer ![]() $c(\Pi )$, depending only on
$c(\Pi )$, depending only on ![]() $\Pi$, such that for any prime
$\Pi$, such that for any prime ![]() $\ell$ satisfying
$\ell$ satisfying ![]() $\ell > c(\Pi )$, and any cyclic extension
$\ell > c(\Pi )$, and any cyclic extension ![]() $K'/K$ of degree
$K'/K$ of degree ![]() $\ell$, there is an automorphic representation
$\ell$, there is an automorphic representation ![]() $\Pi '$ of
$\Pi '$ of ![]() $G({\mathbb {A}}_{K'})$ attached to the
$G({\mathbb {A}}_{K'})$ attached to the ![]() $L$-parameter
$L$-parameter ![]() $\sigma _{\Pi, \lambda }|_{\operatorname {Gal}((K')^{\rm s}/K')}$.
$\sigma _{\Pi, \lambda }|_{\operatorname {Gal}((K')^{\rm s}/K')}$.
Proof. Let ![]() ${\overline {\sigma }}_{\Pi, \lambda }$ denote the reduction of
${\overline {\sigma }}_{\Pi, \lambda }$ denote the reduction of ![]() $\sigma _{\Pi,\lambda }$ modulo
$\sigma _{\Pi,\lambda }$ modulo ![]() $\lambda$; let
$\lambda$; let ![]() $k_\lambda$ denote the residue field of
$k_\lambda$ denote the residue field of ![]() $\lambda$. Our hypothesis on the Mumford–Tate group of
$\lambda$. Our hypothesis on the Mumford–Tate group of ![]() $\Pi$, together with the main theorem of [Reference Böckle, Gajda and PetersenBGP19], implies that the image of
$\Pi$, together with the main theorem of [Reference Böckle, Gajda and PetersenBGP19], implies that the image of ![]() ${\overline {\sigma }}_{\Pi, \lambda }(\Gamma _{K(\zeta _\ell )})$ contains
${\overline {\sigma }}_{\Pi, \lambda }(\Gamma _{K(\zeta _\ell )})$ contains ![]() ${\widehat {G}}(k_\lambda )^+$ for all
${\widehat {G}}(k_\lambda )^+$ for all ![]() $\lambda$ of sufficiently large characteristic. It then follows from Lemma 3.8 that there is a constant
$\lambda$ of sufficiently large characteristic. It then follows from Lemma 3.8 that there is a constant ![]() $b_1(\Pi )$ such that for
$b_1(\Pi )$ such that for ![]() $\ell > b_1(\Pi )$ the image of
$\ell > b_1(\Pi )$ the image of ![]() ${\overline {\sigma }}_{\Pi, \lambda }(\Gamma _{K'(\zeta _\ell )})$ is abundant, and that
${\overline {\sigma }}_{\Pi, \lambda }(\Gamma _{K'(\zeta _\ell )})$ is abundant, and that ![]() ${\overline {\sigma }}_{\Pi, \lambda }$ is also absolutely irreducible.
${\overline {\sigma }}_{\Pi, \lambda }$ is also absolutely irreducible.
Now, it follows from Theorem 5.1 that there is a constant ![]() $b_2(\Pi )$ such that for all
$b_2(\Pi )$ such that for all ![]() $\ell > b_2(\Pi )$, the restriction of
$\ell > b_2(\Pi )$, the restriction of ![]() ${\overline {\sigma }}_{\Pi, \lambda }$ to
${\overline {\sigma }}_{\Pi, \lambda }$ to ![]() $\Gamma _{K'}$ satisfies condition (v) of Theorem 4.6. Taking
$\Gamma _{K'}$ satisfies condition (v) of Theorem 4.6. Taking ![]() $c (\Pi ) := \max (b_1(\Pi ), b_2(\Pi ))$, we may then invoke Theorem 6.2 and Lemma 6.1 to apply Theorem 4.6. The freeneess guarantees the existence of an eigenform supported over a single point on the generic fiber of
$c (\Pi ) := \max (b_1(\Pi ), b_2(\Pi ))$, we may then invoke Theorem 6.2 and Lemma 6.1 to apply Theorem 4.6. The freeneess guarantees the existence of an eigenform supported over a single point on the generic fiber of ![]() $R_{\overline {\sigma }_{\mathfrak m}, |N|, {\mathcal {D}}}$, and we may take
$R_{\overline {\sigma }_{\mathfrak m}, |N|, {\mathcal {D}}}$, and we may take ![]() $\Pi '$ to be an irreducible cuspidal subquotient of the automorphic representation generated by it.
$\Pi '$ to be an irreducible cuspidal subquotient of the automorphic representation generated by it.
7. Local cyclic base change
Now let ![]() $F$ be a local function field. In this section we will prove a local analog of Theorem 6.3, establishing existence of cyclic base change for irreducible smooth representations of
$F$ be a local function field. In this section we will prove a local analog of Theorem 6.3, establishing existence of cyclic base change for irreducible smooth representations of ![]() $G(F)$, along any
$G(F)$, along any ![]() $\mathbb {Z}/\ell \mathbb {Z}$-extension of
$\mathbb {Z}/\ell \mathbb {Z}$-extension of ![]() $F$ for almost all
$F$ for almost all ![]() $\ell$.
$\ell$.
7.1 The Genestier–Lafforgue correspondence
Let ![]() $F$ be a local function field with ring of integers
$F$ be a local function field with ring of integers ![]() ${\mathcal {O}}_F$ and residue characteristic
${\mathcal {O}}_F$ and residue characteristic ![]() $\ell \neq p$. Let
$\ell \neq p$. Let ![]() $W_F$ be the Weil group of
$W_F$ be the Weil group of ![]() $F$. Let
$F$. Let ![]() $G$ be a reductive group over
$G$ be a reductive group over ![]() $F$. In [Reference Genestier and LafforgueGL17, Théorèm 0.1], Genestier and Lafforgue construct a map
$F$. In [Reference Genestier and LafforgueGL17, Théorèm 0.1], Genestier and Lafforgue construct a map
We shall use the two properties of the correspondence ![]() $\pi \mapsto \sigma _{\pi }$ recalled below.
$\pi \mapsto \sigma _{\pi }$ recalled below.
7.1.1 Local–global compatibility
For any automorphic representation ![]() $\Pi \cong \bigotimes _{x \in |X|} \Pi _x$ of
$\Pi \cong \bigotimes _{x \in |X|} \Pi _x$ of ![]() $G(\mathbb {A}_K)$ that is associated to the
$G(\mathbb {A}_K)$ that is associated to the ![]() $L$-parameter
$L$-parameter ![]() $\sigma _{\Pi }$ by V. Lafforgue's global Langlands parametrization (§ 4.2),
$\sigma _{\Pi }$ by V. Lafforgue's global Langlands parametrization (§ 4.2), ![]() $\sigma _{\Pi _x}$ is conjugate to the semisimplification of
$\sigma _{\Pi _x}$ is conjugate to the semisimplification of ![]() $\sigma |_{W_{K_x}}$ for any
$\sigma |_{W_{K_x}}$ for any ![]() $\sigma \in \underline {\rho }_{\Pi }$ (notation as in Remark 4.2).
$\sigma \in \underline {\rho }_{\Pi }$ (notation as in Remark 4.2).
7.1.2 Compatibility with parabolic induction
If ![]() $P$ is a parabolic subgroup of
$P$ is a parabolic subgroup of ![]() $G$ with Levi quotient
$G$ with Levi quotient ![]() $M$,
$M$, ![]() $\tau$ is an irreducible admissible representation of
$\tau$ is an irreducible admissible representation of ![]() $M(F)$, and
$M(F)$, and ![]() $\pi$ is an irreducible subquotient of
$\pi$ is an irreducible subquotient of ![]() $\operatorname {Ind}_{P(F)}^{G(F)} \tau$ (with parabolic induction formed using the unitary normalization), then
$\operatorname {Ind}_{P(F)}^{G(F)} \tau$ (with parabolic induction formed using the unitary normalization), then ![]() $\sigma _{\pi }$ is conjugate to the composition
$\sigma _{\pi }$ is conjugate to the composition ![]() $W_F \xrightarrow {\sigma _{\tau }} \widehat {M}(\overline {\mathbb {Q}}_{\ell }) \hookrightarrow \widehat {G}(\overline {\mathbb {Q}}_{\ell })$.
$W_F \xrightarrow {\sigma _{\tau }} \widehat {M}(\overline {\mathbb {Q}}_{\ell }) \hookrightarrow \widehat {G}(\overline {\mathbb {Q}}_{\ell })$.
7.2 Existence of almost all cyclic base changes in characteristic 0
Definition 7.1 Let ![]() $\pi$ be an irreducible admissible representation of
$\pi$ be an irreducible admissible representation of ![]() $G(F)$ over
$G(F)$ over ![]() $\overline {\mathbb {Q}}_{\ell }$. For a separable field extension
$\overline {\mathbb {Q}}_{\ell }$. For a separable field extension ![]() $F'/F$, we say that an irreducible admissible representation
$F'/F$, we say that an irreducible admissible representation ![]() $\pi '$ of
$\pi '$ of ![]() $G(F')$ over
$G(F')$ over ![]() $\overline {\mathbb {Q}}_{\ell }$ is a base change lifting of
$\overline {\mathbb {Q}}_{\ell }$ is a base change lifting of ![]() $\pi$ to
$\pi$ to ![]() $G(F')$ if
$G(F')$ if ![]() $\sigma _{\pi '} \cong \sigma _{\pi }|_{W_{F'}}$.
$\sigma _{\pi '} \cong \sigma _{\pi }|_{W_{F'}}$.
This definition is an approximation to the notion of base change for ![]() $L$-packets. An
$L$-packets. An ![]() $L$-packet for
$L$-packet for ![]() $G(F')$ should be said to be a base change lifting of an
$G(F')$ should be said to be a base change lifting of an ![]() $L$-packet for
$L$-packet for ![]() $G(F)$ if the corresponding
$G(F)$ if the corresponding ![]() $L$-parameters are related by restriction on Weil groups. Since we lack a definition of
$L$-parameters are related by restriction on Weil groups. Since we lack a definition of ![]() $L$-packets for general groups and representations, we use the fibers of the Genestier–Lafforgue correspondence as a substitute for
$L$-packets for general groups and representations, we use the fibers of the Genestier–Lafforgue correspondence as a substitute for ![]() $L$-packets.
$L$-packets.
Theorem 7.2 Assume that ![]() $p$ is good for
$p$ is good for ![]() $G$ if
$G$ if ![]() $G$ is not simply laced. Let
$G$ is not simply laced. Let ![]() $\pi$ be an irreducible admissible representation of
$\pi$ be an irreducible admissible representation of ![]() $G(F)$ over
$G(F)$ over ![]() $\overline {\mathbb {Q}}$. There exists a constant
$\overline {\mathbb {Q}}$. There exists a constant ![]() $c(\pi )$ such that for all primes
$c(\pi )$ such that for all primes ![]() $\ell > c(\pi )$, for any
$\ell > c(\pi )$, for any ![]() $\mathbb {Z}/\ell \mathbb {Z}$-extension
$\mathbb {Z}/\ell \mathbb {Z}$-extension ![]() $F'/F$ there exists a base change lifting of
$F'/F$ there exists a base change lifting of ![]() $\pi$ to
$\pi$ to ![]() $G(F')$.
$G(F')$.
Remark 7.3 In [Reference FengFen24, Theorem 1.1], a version of this result was established for mod ![]() $\ell$ representations, when the extension is cyclic of degree equal to the same prime
$\ell$ representations, when the extension is cyclic of degree equal to the same prime ![]() $\ell$, by completely different methods.
$\ell$, by completely different methods.
Proposition 7.4 Assume that ![]() $p$ is good for
$p$ is good for ![]() $G$ if
$G$ if ![]() $G$ is not simply laced. Let
$G$ is not simply laced. Let ![]() $\pi$ be an irreducible admissible supercuspidal representation of
$\pi$ be an irreducible admissible supercuspidal representation of ![]() $G(F)$ over
$G(F)$ over ![]() $\overline {\mathbb {Q}}$. Then there exist a global field
$\overline {\mathbb {Q}}$. Then there exist a global field ![]() $K$ and a place
$K$ and a place ![]() $v \in |K|$ with
$v \in |K|$ with ![]() $K_v \cong F$, and a cuspidal automorphic representation
$K_v \cong F$, and a cuspidal automorphic representation ![]() $\Pi$ of
$\Pi$ of ![]() $G(\mathbb {A}_K\!)$ with Mumford–Tate group
$G(\mathbb {A}_K\!)$ with Mumford–Tate group ![]() ${\widehat {G}}$ such that
${\widehat {G}}$ such that ![]() $\Pi _v \cong \pi$.
$\Pi _v \cong \pi$.
Proof Proof of Theorem 7.2 assuming Proposition 7.4
First we reduce to the case where ![]() $\pi$ is supercuspidal. Indeed, any
$\pi$ is supercuspidal. Indeed, any ![]() $\pi$ can be realized as an irreducible subquotient of a parabolic induction of supercuspidal representations, of the form
$\pi$ can be realized as an irreducible subquotient of a parabolic induction of supercuspidal representations, of the form ![]() $\operatorname {Ind}_{P(F)}^{G(F)} \tau$. By § 7.1.2, the parabolic induction from
$\operatorname {Ind}_{P(F)}^{G(F)} \tau$. By § 7.1.2, the parabolic induction from ![]() $M(F')$ to
$M(F')$ to ![]() $G(F')$ of a base change of
$G(F')$ of a base change of ![]() $\tau$ to
$\tau$ to ![]() $M(F' )$ will have an
$M(F' )$ will have an ![]() $L$-parameter of the desired form. So it suffices to treat the supercuspidal case.
$L$-parameter of the desired form. So it suffices to treat the supercuspidal case.
Hence we may and do assume for the rest of the argument that ![]() $\pi$ is supercuspidal. Then we may apply Proposition 7.4 to embed
$\pi$ is supercuspidal. Then we may apply Proposition 7.4 to embed ![]() $\pi$ as the local component at
$\pi$ as the local component at ![]() $v$ of cuspidal automorphic representation
$v$ of cuspidal automorphic representation ![]() $\Pi$ over a global field
$\Pi$ over a global field ![]() $K$ with
$K$ with ![]() $K_v \cong F$. Using Remark 4.2, we can replace
$K_v \cong F$. Using Remark 4.2, we can replace ![]() $\Pi$ by an isomorphic
$\Pi$ by an isomorphic ![]() $G(\mathbb {A}_K)$-representation (realized differently in the space of cuspidal functions on
$G(\mathbb {A}_K)$-representation (realized differently in the space of cuspidal functions on ![]() $G(K) \backslash G(\mathbb {A}_K)$) to assume that
$G(K) \backslash G(\mathbb {A}_K)$) to assume that ![]() $\Pi$ is attached to an
$\Pi$ is attached to an ![]() $L$-parameter
$L$-parameter ![]() $\sigma _{\Pi }$. Then Theorem 6.3 applies, so let
$\sigma _{\Pi }$. Then Theorem 6.3 applies, so let ![]() $c(\pi ) := c(\Pi )$ be as in Theorem 6.3. For any
$c(\pi ) := c(\Pi )$ be as in Theorem 6.3. For any ![]() $\mathbb {Z}/\ell \mathbb {Z}$-extension
$\mathbb {Z}/\ell \mathbb {Z}$-extension ![]() $F'/F$, we can find a
$F'/F$, we can find a ![]() $\mathbb {Z}/\ell \mathbb {Z}$-extension
$\mathbb {Z}/\ell \mathbb {Z}$-extension ![]() $K'/K$ with a place
$K'/K$ with a place ![]() $v'$ lying over
$v'$ lying over ![]() $v$ such that
$v$ such that ![]() $K_{v'} \cong F'$. By Theorem 6.3, there exists a cuspidal automorphic representation
$K_{v'} \cong F'$. By Theorem 6.3, there exists a cuspidal automorphic representation ![]() $\Pi '$ of
$\Pi '$ of ![]() $G(\mathbb {A}_{K'})$ with
$G(\mathbb {A}_{K'})$ with ![]() $L$-parameter
$L$-parameter ![]() $\sigma _{\Pi '} \cong \sigma _{\Pi }|_{\Gamma _{K'}}$. If
$\sigma _{\Pi '} \cong \sigma _{\Pi }|_{\Gamma _{K'}}$. If ![]() $\Pi '_{v'}$ is the local component of
$\Pi '_{v'}$ is the local component of ![]() $\Pi '$ at
$\Pi '$ at ![]() $v'$, then the local–global compatibility of § 7.1.1 ensures that
$v'$, then the local–global compatibility of § 7.1.1 ensures that ![]() $\sigma _{\Pi '_{v'}} \cong \sigma _{\Pi '}|_{W_{K'_{v'}}}$, hence
$\sigma _{\Pi '_{v'}} \cong \sigma _{\Pi '}|_{W_{K'_{v'}}}$, hence
so ![]() $\Pi '_{v'}$ is the desired local base change.
$\Pi '_{v'}$ is the desired local base change.
Remark 7.5 Since every supercuspidal representation of ![]() $G(F)$ admits a model over
$G(F)$ admits a model over ![]() $\overline {\mathbb {Q}}$, at least after twisting by a central character (which is unnecessary for us because our
$\overline {\mathbb {Q}}$, at least after twisting by a central character (which is unnecessary for us because our ![]() $G$ is semisimple), Theorem 7.2 applies to all supercuspidal representations. In fact, we may present any irreducible admissible representation in terms of parabolic inductions and twists of representations defined over
$G$ is semisimple), Theorem 7.2 applies to all supercuspidal representations. In fact, we may present any irreducible admissible representation in terms of parabolic inductions and twists of representations defined over ![]() $\overline {\mathbb {Q}}$, and then the compatibility of the Genestier–Lafforgue correspondence with parabolic induction and twisting would allow the formulation of a meaningful extension of Theorem 7.2 to all irreducible admissible representations.
$\overline {\mathbb {Q}}$, and then the compatibility of the Genestier–Lafforgue correspondence with parabolic induction and twisting would allow the formulation of a meaningful extension of Theorem 7.2 to all irreducible admissible representations.
7.3 Globalization of supercuspidal representations
This subsection is devoted to the proof of Proposition 7.4. We will use an argument due to Beuzart-Plessis, based on the Deligne–Kazhdan simple trace formula, to construct a globalization ![]() $\Pi$ of
$\Pi$ of ![]() $\pi$ with specified local components at several auxiliary places that automatically force the image of Lafforgue's corresponding parameter to be Zariski dense.
$\pi$ with specified local components at several auxiliary places that automatically force the image of Lafforgue's corresponding parameter to be Zariski dense.
7.3.1 Genestier–Lafforgue parameters of simple supercuspidals
The notion of ‘simple supercuspidal representations’ was singled out by Gross and Reeder [Reference Gross and ReederGR10]. Let us recall the definition.
Definition 7.6 Let ![]() $G$ be a split semisimple group over a non-archimedean local field
$G$ be a split semisimple group over a non-archimedean local field ![]() $F$ of residue characteristic
$F$ of residue characteristic ![]() $p \neq \ell$. A simple supercuspidal representation is a representation ‘
$p \neq \ell$. A simple supercuspidal representation is a representation ‘![]() $V_{\phi }$’ of
$V_{\phi }$’ of ![]() $G(F)$ that arises in the following way. Let
$G(F)$ that arises in the following way. Let ![]() $B \subset G$ be a Borel subgroup, with unipotent radical
$B \subset G$ be a Borel subgroup, with unipotent radical ![]() $U$. Let
$U$. Let ![]() $I \subset G({\mathcal {O}}_F)$ be the corresponding Iwahori subgroup, and
$I \subset G({\mathcal {O}}_F)$ be the corresponding Iwahori subgroup, and ![]() $I(1) \subset I$ its pro-unipotent radical. For an affine generic character
$I(1) \subset I$ its pro-unipotent radical. For an affine generic character ![]() $\phi \colon I(1) \rightarrow \mathbb {Q}_{\ell }(\mu _p)$, we define
$\phi \colon I(1) \rightarrow \mathbb {Q}_{\ell }(\mu _p)$, we define ![]() $V_{\phi } := \operatorname {c-Ind}_{I(1) \times Z(G)}^{G(F)} (\phi \otimes \unicode{x1D7D9})$.
$V_{\phi } := \operatorname {c-Ind}_{I(1) \times Z(G)}^{G(F)} (\phi \otimes \unicode{x1D7D9})$.
Gross and Reeder showed that simple supercuspidal representations are irreducible and supercuspidal. They anticipated the shape of the associated ![]() $L$-parameters. To explain this, let
$L$-parameters. To explain this, let ![]() ${\mathcal {J}} \subset W_{F}$ be the inertia subgroup. Let us call simple supercuspidal parameter a discreteFootnote 7 Langlands parameter
${\mathcal {J}} \subset W_{F}$ be the inertia subgroup. Let us call simple supercuspidal parameter a discreteFootnote 7 Langlands parameter ![]() $\sigma \colon W_F \rightarrow \widehat {G}(\overline {\mathbb {Q}}_{\ell })$ such that the adjoint representation
$\sigma \colon W_F \rightarrow \widehat {G}(\overline {\mathbb {Q}}_{\ell })$ such that the adjoint representation ![]() $\operatorname {Ad} \circ \sigma$ has
$\operatorname {Ad} \circ \sigma$ has ![]() $\widehat {\mathfrak {g}}^{{\mathcal {J}}} =0$ and Swan conductor equal to the rank of
$\widehat {\mathfrak {g}}^{{\mathcal {J}}} =0$ and Swan conductor equal to the rank of ![]() $\widehat {G}$. We emphasize that a discrete Langlands parameter, a fortiori a simple supercuspidal parameter, is already semisimple; this will be used when invoking the local–global compatibility of § 7.1.1.
$\widehat {G}$. We emphasize that a discrete Langlands parameter, a fortiori a simple supercuspidal parameter, is already semisimple; this will be used when invoking the local–global compatibility of § 7.1.1.
Proposition 7.7 Assume that ![]() $p$ is good for
$p$ is good for ![]() $G$ if
$G$ if ![]() $G$ is not simply laced. Then the Genestier–Lafforgue parameter of
$G$ is not simply laced. Then the Genestier–Lafforgue parameter of ![]() $V_{\phi }$ is a simple supercuspidal parameter.
$V_{\phi }$ is a simple supercuspidal parameter.
Proof. The idea is to find a globalization of ![]() $V_{\phi }$ to a cuspidal automorphic representation on
$V_{\phi }$ to a cuspidal automorphic representation on ![]() $\mathbf {P}^1$, whose associated global
$\mathbf {P}^1$, whose associated global ![]() $L$-parameter can be computed explicitly. A particularly convenient such globalization was studied by Heinloth, Ngô, and Yun [Reference Heinloth, Ngô and YunHNY13] and we only need to collect the relevant consequences of their work.
$L$-parameter can be computed explicitly. A particularly convenient such globalization was studied by Heinloth, Ngô, and Yun [Reference Heinloth, Ngô and YunHNY13] and we only need to collect the relevant consequences of their work.
Let ![]() $K = \mathbb {F}_q(\mathbf {P}^1)=\mathbb {F}_q(t)$. Let
$K = \mathbb {F}_q(\mathbf {P}^1)=\mathbb {F}_q(t)$. Let ![]() $I_0$ be the Iwahori subgroup of
$I_0$ be the Iwahori subgroup of ![]() $G(\mathbb {F}_q((t)))$, and
$G(\mathbb {F}_q((t)))$, and ![]() $I(1)_{\infty }$ be the pro-unipotent radical of the Iwahori subgroup of
$I(1)_{\infty }$ be the pro-unipotent radical of the Iwahori subgroup of ![]() $G(\mathbb {F}_q((1/t)))$. As a special case of [Reference YunYun16, Proposition 2.7], there is a unique automorphic representation
$G(\mathbb {F}_q((1/t)))$. As a special case of [Reference YunYun16, Proposition 2.7], there is a unique automorphic representation ![]() $\Pi \cong \bigotimes '_{x \in |\mathbf {P}^1|} \Pi _x$ of
$\Pi \cong \bigotimes '_{x \in |\mathbf {P}^1|} \Pi _x$ of ![]() $G(\mathbb {A}_K)$ such that:
$G(\mathbb {A}_K)$ such that:
•
 $\Pi _x$ is unramified if
$\Pi _x$ is unramified if  $x \neq 0, \infty$;
$x \neq 0, \infty$;•
 $\Pi _0$ has a vector invariant under
$\Pi _0$ has a vector invariant under  $I_0$;
$I_0$;•
 $\Pi _{\infty }$ has an eigenvector under
$\Pi _{\infty }$ has an eigenvector under  $I(1)_{\infty }$, on which the action is given by
$I(1)_{\infty }$, on which the action is given by  $\phi$.
$\phi$.
Moreover, this ![]() $\Pi$ is cuspidal and appears with multiplicity one in the automorphic spectrum, and
$\Pi$ is cuspidal and appears with multiplicity one in the automorphic spectrum, and
 \[ \dim C_c^{\infty} \bigg( G(K) \backslash G(\mathbb{A}_K) / \prod_{x \neq 0, \infty} G({\mathcal{O}}_x), \overline{\mathbb{Q}} \bigg)^{I_0 \times (I(1)_{\infty}, \phi)} = 1. \]
\[ \dim C_c^{\infty} \bigg( G(K) \backslash G(\mathbb{A}_K) / \prod_{x \neq 0, \infty} G({\mathcal{O}}_x), \overline{\mathbb{Q}} \bigg)^{I_0 \times (I(1)_{\infty}, \phi)} = 1. \]
Since the excursion algebra acts on this one-dimensional ![]() $\overline {\mathbb {Q}}_{\ell }$-vector space, its action is automatically through a character, which determines the
$\overline {\mathbb {Q}}_{\ell }$-vector space, its action is automatically through a character, which determines the ![]() $L$-parameter
$L$-parameter ![]() $\sigma _{\Pi }$ associated to
$\sigma _{\Pi }$ associated to ![]() $\Pi$ by Lafforgue's correspondence.
$\Pi$ by Lafforgue's correspondence.
In this case, Heinloth, Ngô, and Yun construct a Hecke eigensheaf ![]() $A_{\phi }$ on a moduli stack
$A_{\phi }$ on a moduli stack ![]() $\operatorname {Bun}_{G(0,2)}$ of
$\operatorname {Bun}_{G(0,2)}$ of ![]() $G$-bundles on
$G$-bundles on ![]() $\mathbf {P}^1$ with level structure at
$\mathbf {P}^1$ with level structure at ![]() $0$ and
$0$ and ![]() $\infty$, whose associated Frobenius trace function is a non-zero
$\infty$, whose associated Frobenius trace function is a non-zero ![]() $f_{\phi } \in C_c^{\infty } \big ( G(K) \backslash G(\mathbb {A}_K) / \prod _{x \neq 0, \infty } G({\mathcal {O}}_x), \overline {\mathbb {Q}} \big )^{I_0 \times (I(1)_{\infty }, \phi )}$. They further prove that
$f_{\phi } \in C_c^{\infty } \big ( G(K) \backslash G(\mathbb {A}_K) / \prod _{x \neq 0, \infty } G({\mathcal {O}}_x), \overline {\mathbb {Q}} \big )^{I_0 \times (I(1)_{\infty }, \phi )}$. They further prove that ![]() $A_{\phi }$ is a Hecke eigensheaf, with corresponding local system the (generalized) Kloosterman local system
$A_{\phi }$ is a Hecke eigensheaf, with corresponding local system the (generalized) Kloosterman local system ![]() $\mathrm {Kl}_{\widehat {G}}(\phi ) \colon \pi _1(\mathbb {P}^1 - \{0, \infty \}, \widehat {G}(\overline {\mathbb {Q}}_{\ell }))$. By [Reference Heinloth, Ngô and YunHNY13, Theorem 2, Corollary 2.15], letting
$\mathrm {Kl}_{\widehat {G}}(\phi ) \colon \pi _1(\mathbb {P}^1 - \{0, \infty \}, \widehat {G}(\overline {\mathbb {Q}}_{\ell }))$. By [Reference Heinloth, Ngô and YunHNY13, Theorem 2, Corollary 2.15], letting ![]() ${\mathcal {J}}_{\infty } \subset W_{K_{\infty }}$ be the inertia group at
${\mathcal {J}}_{\infty } \subset W_{K_{\infty }}$ be the inertia group at ![]() $\infty$, the local monodromy representation
$\infty$, the local monodromy representation ![]() $\mathrm {Kl}_{\widehat {G}}(\phi )|_{{\mathcal {J}}_{\infty }} \colon {\mathcal {J}}_{\infty } \rightarrow \widehat {G}(\overline {\mathbb {Q}}_{\ell })$ at
$\mathrm {Kl}_{\widehat {G}}(\phi )|_{{\mathcal {J}}_{\infty }} \colon {\mathcal {J}}_{\infty } \rightarrow \widehat {G}(\overline {\mathbb {Q}}_{\ell })$ at ![]() $\infty$ is irreducible and it is the restriction to
$\infty$ is irreducible and it is the restriction to ![]() ${\mathcal {J}}_\infty$ of a simple supercuspidal parameter.
${\mathcal {J}}_\infty$ of a simple supercuspidal parameter.
By [Reference Böckle, Harris, Khare and ThorneBHKT19, Proposition 6.4], the parameter associated to ![]() $f_{\phi }$ by Lafforgue's correspondence must coincide with
$f_{\phi }$ by Lafforgue's correspondence must coincide with ![]() $\mathrm {Kl}_{\widehat {G}}(\phi )$. By local–global compatibility, the Genestier–Lafforgue parameter of
$\mathrm {Kl}_{\widehat {G}}(\phi )$. By local–global compatibility, the Genestier–Lafforgue parameter of ![]() $V_{\phi }$ therefore agrees upon restriction to
$V_{\phi }$ therefore agrees upon restriction to ![]() ${\mathcal {J}}_{\infty }$ with
${\mathcal {J}}_{\infty }$ with ![]() $\mathrm {Kl}_{\widehat {G}}(\phi )|_{{\mathcal {J}}_{\infty }}$.
$\mathrm {Kl}_{\widehat {G}}(\phi )|_{{\mathcal {J}}_{\infty }}$.
7.3.2 Globalization
The following lemma is proved by Beuzart-Plessis in the appendix to [Reference Gan, Harris and SawinGHS21], using the Deligne–Kazhdan simple trace formula.
Lemma 7.8 Let ![]() $\pi$ be a supercuspidal representation of
$\pi$ be a supercuspidal representation of ![]() $G(F)$ over
$G(F)$ over ![]() $\overline {\mathbb {Q}}$. There exists a global curve
$\overline {\mathbb {Q}}$. There exists a global curve ![]() $X$, with function field
$X$, with function field ![]() $K = \mathbb {F}_q(X)$ and places
$K = \mathbb {F}_q(X)$ and places ![]() $v,w,w', w'' \in |X|$, and a cuspidal representation
$v,w,w', w'' \in |X|$, and a cuspidal representation ![]() $\Pi \cong \bigotimes '_{x \in |X|} \Pi _x$ of
$\Pi \cong \bigotimes '_{x \in |X|} \Pi _x$ of ![]() $G(\mathbb {A}_K)$ such that the following statements hold:
$G(\mathbb {A}_K)$ such that the following statements hold:
(i)
 $K_v \cong F$ and
$K_v \cong F$ and  $\Pi _v \cong \pi$ as
$\Pi _v \cong \pi$ as  $G(F)$-representations.
$G(F)$-representations.(ii)
 $\Pi _w$ is a simple supercuspidal representation of
$\Pi _w$ is a simple supercuspidal representation of  $G(K_w)$.
$G(K_w)$.(iii)
 $\Pi _{w'}$ has non-zero trace against the pseudo-coefficient for the Steinberg representation given by the Euler-Poincaré function [Reference LaumonLau96, Theorem 8.2.1].
$\Pi _{w'}$ has non-zero trace against the pseudo-coefficient for the Steinberg representation given by the Euler-Poincaré function [Reference LaumonLau96, Theorem 8.2.1].(iv)
 $\Pi _{w''}$ is an unramified representation parametrized by a regular element of
$\Pi _{w''}$ is an unramified representation parametrized by a regular element of  $\widehat {T}//W$. Moreover, the parameter can be chosen to avoid any finite union of proper subtori of
$\widehat {T}//W$. Moreover, the parameter can be chosen to avoid any finite union of proper subtori of  $\widehat {T}$.
$\widehat {T}$.
We will need a characterization of irreducible subgroups of ![]() $\widehat {G}$ containing a principal unipotent element. The following result is probably known but we were unable to find a reference.
$\widehat {G}$ containing a principal unipotent element. The following result is probably known but we were unable to find a reference.
Lemma 7.9 Let ![]() ${\mathfrak g}$ be a semisimple Lie algebra and
${\mathfrak g}$ be a semisimple Lie algebra and ![]() ${\mathfrak h}$ a proper semisimple subalgebra containing a regular nilpotent element of
${\mathfrak h}$ a proper semisimple subalgebra containing a regular nilpotent element of ![]() ${\mathfrak g}$. Then the rank of
${\mathfrak g}$. Then the rank of ![]() ${\mathfrak h}$ is strictly less than that of
${\mathfrak h}$ is strictly less than that of ![]() ${\mathfrak g}$.
${\mathfrak g}$.
Proof. Let ![]() $E$ be the regular nilpotent of
$E$ be the regular nilpotent of ![]() ${\mathfrak g}$ which lies in
${\mathfrak g}$ which lies in ![]() ${\mathfrak h}$. We first claim that
${\mathfrak h}$. We first claim that ![]() $E$ is also regular in
$E$ is also regular in ![]() ${\mathfrak h}$. We can complete
${\mathfrak h}$. We can complete ![]() $E$ to an
$E$ to an ![]() $\mathfrak {sl}_2$-triple
$\mathfrak {sl}_2$-triple ![]() $(E, H, F)$ in
$(E, H, F)$ in ![]() ${\mathfrak h}$. The element
${\mathfrak h}$. The element ![]() $H$ is regular semisimple in
$H$ is regular semisimple in ![]() ${\mathfrak g}$, hence in
${\mathfrak g}$, hence in ![]() ${\mathfrak h}$, which implies by [Reference BourbakiBou05, VIII. 11.4, Proposition 7] that
${\mathfrak h}$, which implies by [Reference BourbakiBou05, VIII. 11.4, Proposition 7] that ![]() $E$ is regular nilpotent in
$E$ is regular nilpotent in ![]() ${\mathfrak h}$.
${\mathfrak h}$.
Let ![]() $r({\mathfrak g})$ and
$r({\mathfrak g})$ and ![]() $\ell ({\mathfrak g})$ denote respectively the ranks of
$\ell ({\mathfrak g})$ denote respectively the ranks of ![]() ${\mathfrak g}$ and its length as a representation of the three-dimensional subalgebra spanned by
${\mathfrak g}$ and its length as a representation of the three-dimensional subalgebra spanned by ![]() $(E,H,F)$; define
$(E,H,F)$; define ![]() $r({\mathfrak h})$ and
$r({\mathfrak h})$ and ![]() $\ell ({\mathfrak h})$ analogously. The proposition just cited from [Reference BourbakiBou05] implies that
$\ell ({\mathfrak h})$ analogously. The proposition just cited from [Reference BourbakiBou05] implies that
Thus ![]() $r({\mathfrak g}) = r({\mathfrak h})$ if and only if
$r({\mathfrak g}) = r({\mathfrak h})$ if and only if ![]() ${\mathfrak g}$ and its subspace
${\mathfrak g}$ and its subspace ![]() ${\mathfrak h}$ have the same length as
${\mathfrak h}$ have the same length as ![]() $(E,H,F)$-modules; but this is only possible if
$(E,H,F)$-modules; but this is only possible if ![]() ${\mathfrak g} = {\mathfrak h}$.
${\mathfrak g} = {\mathfrak h}$.
Corollary 7.10 Let ![]() ${\mathcal {H}}$ denote the set of conjugacy classes of proper semisimple subgroups of
${\mathcal {H}}$ denote the set of conjugacy classes of proper semisimple subgroups of ![]() $\widehat {G}$ containing a principal unipotent element, and for each
$\widehat {G}$ containing a principal unipotent element, and for each ![]() $H \in {\mathcal {H}}$, let
$H \in {\mathcal {H}}$, let ![]() $\widehat {T}_H \subset \widehat {T}//W$ denote the image of a maximal torus of
$\widehat {T}_H \subset \widehat {T}//W$ denote the image of a maximal torus of ![]() $H$ (which is independent of the choice of representative). Then the complement of the union of the
$H$ (which is independent of the choice of representative). Then the complement of the union of the ![]() $\widehat {T}_H$ is Zariski dense in
$\widehat {T}_H$ is Zariski dense in ![]() $\widehat {T}//W$.
$\widehat {T}//W$.
Proof. A classification of ![]() ${\mathcal {H}}$ in all types appears in [Reference Saxl and SeitzSS97, Theorem A, Theorem B] (in characteristic 0, the result has been credited to earlier work of Dynkin). It is finite. On the other hand, it follows from Lemma 7.9 that each
${\mathcal {H}}$ in all types appears in [Reference Saxl and SeitzSS97, Theorem A, Theorem B] (in characteristic 0, the result has been credited to earlier work of Dynkin). It is finite. On the other hand, it follows from Lemma 7.9 that each ![]() $\widehat {T}_H$ is of codimension at least
$\widehat {T}_H$ is of codimension at least ![]() $1$ in
$1$ in ![]() $\widehat {T}//W$ (this is also clear from inspection of
$\widehat {T}//W$ (this is also clear from inspection of ![]() ${\mathcal {H}}$). Therefore,
${\mathcal {H}}$). Therefore, ![]() $\bigcup _{H \in {\mathcal {H}}} \widehat {T}_H$ is a finite union of positive-codimension subvarieties in
$\bigcup _{H \in {\mathcal {H}}} \widehat {T}_H$ is a finite union of positive-codimension subvarieties in ![]() $\widehat {T}//W$.
$\widehat {T}//W$.
7.3.3 Determination of global monodromy
Let ![]() $\Pi$ be as in Lemma 7.8. Let
$\Pi$ be as in Lemma 7.8. Let ![]() $\underline {\rho }_{\Pi }$ be the set of Remark 4.2 and
$\underline {\rho }_{\Pi }$ be the set of Remark 4.2 and ![]() $\sigma \in \underline {\rho }_{\Pi }$. We claim that
$\sigma \in \underline {\rho }_{\Pi }$. We claim that ![]() $\sigma$ has Zariski dense image. This will complete the proof of Proposition 7.4.
$\sigma$ has Zariski dense image. This will complete the proof of Proposition 7.4.
So it only remains to prove the claim. By local–global compatibility, the semisimplification of ![]() $\sigma |_{K_x}$ corresponds to
$\sigma |_{K_x}$ corresponds to ![]() $\Pi _x$ under the Genestier–Lafforgue correspondence for all
$\Pi _x$ under the Genestier–Lafforgue correspondence for all ![]() $x \in |X|$. By Proposition 7.7 and local–global compatibility, the semisimplification of
$x \in |X|$. By Proposition 7.7 and local–global compatibility, the semisimplification of ![]() $\sigma _{\Pi }|_{K_w}$ is already absolutely irreducible, so
$\sigma _{\Pi }|_{K_w}$ is already absolutely irreducible, so ![]() $\sigma _{\Pi }$ is absolutely irreducible. By [Reference Sawin and TemplierST21, Lemma 11.4], for any representation
$\sigma _{\Pi }$ is absolutely irreducible. By [Reference Sawin and TemplierST21, Lemma 11.4], for any representation ![]() $V$ of
$V$ of ![]() $\widehat {G}$ the corresponding local system is
$\widehat {G}$ the corresponding local system is ![]() $V \circ \sigma _{\Pi }$ is pure of weight
$V \circ \sigma _{\Pi }$ is pure of weight ![]() $0$. By condition (iii) and compatibility of the Genestier–Lafforgue correspondence with parabolic induction,
$0$. By condition (iii) and compatibility of the Genestier–Lafforgue correspondence with parabolic induction, ![]() $\sigma |_{W_{K_{w'}}}$ has the same semisimplification as the Steinberg representation. It follows as in [Reference Heinloth, Ngô and YunHNY13, § 4.3] from purity of the weight-monodromy filtration [Reference DeligneDel80, Theorem I.8.4] that the image of
$\sigma |_{W_{K_{w'}}}$ has the same semisimplification as the Steinberg representation. It follows as in [Reference Heinloth, Ngô and YunHNY13, § 4.3] from purity of the weight-monodromy filtration [Reference DeligneDel80, Theorem I.8.4] that the image of ![]() $\sigma |_{K_{w'}}$ contains a principal unipotent element.
$\sigma |_{K_{w'}}$ contains a principal unipotent element.
By [Reference DeligneDel80, Corollaire I.3.9] and the property that ![]() $V \circ \sigma _{\Pi }$ is pure of weight
$V \circ \sigma _{\Pi }$ is pure of weight ![]() $0$ for every
$0$ for every ![]() $V$, the neutral component of the Zariski closure of the image of
$V$, the neutral component of the Zariski closure of the image of ![]() $\sigma$ in
$\sigma$ in ![]() $\widehat {G}$ is semisimple. Furthermore, we have just seen that it does not lie in any proper parabolic subgroup, and also that it contains a principal unipotent element. By Lemma 7.9, proper semisimple subgroups of
$\widehat {G}$ is semisimple. Furthermore, we have just seen that it does not lie in any proper parabolic subgroup, and also that it contains a principal unipotent element. By Lemma 7.9, proper semisimple subgroups of ![]() $\widehat {G}$ have smaller rank. But this is ruled out by (iv), where the proper subtori are those in the statement of Corollary 7.10.
$\widehat {G}$ have smaller rank. But this is ruled out by (iv), where the proper subtori are those in the statement of Corollary 7.10.
8. Cyclic base change for toral supercuspidal representations
In this section we will investigate cyclic base change more explicitly for the class of toral supercuspidal representations studied in [Reference Chan and OiCO23]. The strategy is to first explicate cyclic base change for the mod ![]() $\ell$ reductions of these representations, using a Conjecture of Treumann-Venkatesh (established in [Reference FengFen24] for the Genestier–Lafforgue correspondence) that ‘base change functoriality is realized by Tate cohomology.’
$\ell$ reductions of these representations, using a Conjecture of Treumann-Venkatesh (established in [Reference FengFen24] for the Genestier–Lafforgue correspondence) that ‘base change functoriality is realized by Tate cohomology.’
The main new work is in calculating the Tate cohomology of toral supercuspidal representations, and what facilitates this calculation is a geometric model for these representations established by Chan and Oi [Reference Chan and OiCO23], as compact inductions from parahoric subgroups of ‘generalized Deligne–Lusztig inductions’ studied by Chan and Ivanov. The generalized Deligne–Lusztig representations are produced from the cohomology of ‘Deligne–Lusztig type varieties’ built out of group schemes coming from the Moy–Prasad filtration, analogously to the way in which Deligne–Lusztig varieties are built from reductive groups over finite fields. Hence our computation naturally divides into two steps: (1) studying Tate cohomology of Deligne–Lusztig type varieties, which we do in § 8.2; and (2) studying Tate cohomology of compact inductions, which we do in § 8.3.
Kaletha constructs an explicit local Langlands parametrization of the toral supercuspidal representations in [Reference KalethaKal19]. On the other hand, we identify base change relations among the Genestier–Lafforgue parameters of toral supercuspidal representations. This gives some evidence for consistency between the Genestier–Lafforgue correspondence [Reference Genestier and LafforgueGL17] and Kaletha's construction of ![]() $L$-packets of regular supercuspidal representations.
$L$-packets of regular supercuspidal representations.
We emphasize that in this section, ![]() $F$ is a non-archimedean local field having residue characteristic
$F$ is a non-archimedean local field having residue characteristic ![]() $p$, but we allow
$p$, but we allow ![]() $F$ to have characteristic
$F$ to have characteristic ![]() $0$ in all results up to Theorem 8.18.
$0$ in all results up to Theorem 8.18.
8.1 Work of Chan and Ivanov
We briefly recall the generalized Deligne–Lusztig representations appearing in [Reference Chan and IvanovCI21].
Let ![]() $G$ be a reductive group over a non-archimedean local field
$G$ be a reductive group over a non-archimedean local field ![]() $F$. Let
$F$. Let ![]() $T \hookrightarrow G$ be an unramified maximal torus and
$T \hookrightarrow G$ be an unramified maximal torus and ![]() $x \in {\mathcal {B}}(G/F)$ be a point of the Bruhat–Tits building of
$x \in {\mathcal {B}}(G/F)$ be a point of the Bruhat–Tits building of ![]() $G$ that lies in the apartment of
$G$ that lies in the apartment of ![]() $T$. If
$T$. If ![]() $F'/F$ is a tamely ramified extension, then we may also regard
$F'/F$ is a tamely ramified extension, then we may also regard ![]() $x$ as a point of
$x$ as a point of ![]() ${\mathcal {B}}(G_{F'}/F')$ using the identification
${\mathcal {B}}(G_{F'}/F')$ using the identification ![]() ${\mathcal {B}}(G/F) = {\mathcal {B}}(G_{F'}/F')^{\operatorname {Gal}(F'/F)}$. Corresponding to
${\mathcal {B}}(G/F) = {\mathcal {B}}(G_{F'}/F')^{\operatorname {Gal}(F'/F)}$. Corresponding to ![]() $x$ we have by Bruhat–Tits theory a parahoric group scheme
$x$ we have by Bruhat–Tits theory a parahoric group scheme ![]() ${\mathcal {G}}/{\mathcal {O}}_F$, whose generic fiber is
${\mathcal {G}}/{\mathcal {O}}_F$, whose generic fiber is ![]() $G/F$.
$G/F$.
Let ![]() $\mathbb {F}_q$ be the residue field of
$\mathbb {F}_q$ be the residue field of ![]() $F$. By assumption,
$F$. By assumption, ![]() $T$ splits over
$T$ splits over ![]() $\breve {F} := W(\overline {\mathbb {F}}_q)$. Let
$\breve {F} := W(\overline {\mathbb {F}}_q)$. Let ![]() $U$ be the unipotent radical of an
$U$ be the unipotent radical of an ![]() $\breve {F}$-rational Borel subgroup of
$\breve {F}$-rational Borel subgroup of ![]() $G_{\breve {F}}$ containing
$G_{\breve {F}}$ containing ![]() $T_{\breve {F}}$.
$T_{\breve {F}}$.
For ![]() $r \in \mathbb {Z}_{\geq 0}$, we have group schemes
$r \in \mathbb {Z}_{\geq 0}$, we have group schemes ![]() $\mathbb {G}_r, \mathbb {T}_r, \mathbb {U}_r$ over
$\mathbb {G}_r, \mathbb {T}_r, \mathbb {U}_r$ over ![]() $\mathbb {F}_q$ as in [Reference Chan and IvanovCI21, § 2.5, 2.6] corresponding to subquotients of the Moy–Prasad filtration at
$\mathbb {F}_q$ as in [Reference Chan and IvanovCI21, § 2.5, 2.6] corresponding to subquotients of the Moy–Prasad filtration at ![]() $x$, such that
$x$, such that
and ![]() $\mathbb {U}_r \subset (\mathbb {G}_r)_{\overline {\mathbb {F}}_q}$.
$\mathbb {U}_r \subset (\mathbb {G}_r)_{\overline {\mathbb {F}}_q}$.
8.1.1 Deep level Deligne–Lusztig varieties
We recall certain schemes constructed in [Reference Chan and IvanovCI21, § 3], generalizing Deligne–Lusztig varieties. Let
(The variety ![]() $S_{\mathbb {T}_r,\mathbb {U}_r}$ is called
$S_{\mathbb {T}_r,\mathbb {U}_r}$ is called ![]() $X_r$ in [Reference Chan and OiCO23].) It is a separated, smooth, finite type scheme over
$X_r$ in [Reference Chan and OiCO23].) It is a separated, smooth, finite type scheme over ![]() $\overline {\mathbb {F}}_q$, with an action of
$\overline {\mathbb {F}}_q$, with an action of ![]() $G_{x,0:r+} \times T_{x,0:r+}$ by multiplication on the left and right, and also a free action of
$G_{x,0:r+} \times T_{x,0:r+}$ by multiplication on the left and right, and also a free action of ![]() $\mathbb {U}_r \cap \operatorname {Fr}_q^{-1} (\mathbb {U}_r)$ by right translation.
$\mathbb {U}_r \cap \operatorname {Fr}_q^{-1} (\mathbb {U}_r)$ by right translation.
It is actually more convenient for us to work with
Since the natural map ![]() $S_{\mathbb {T}_r,\mathbb {U}_r} \rightarrow Y_{\mathbb {T}_r,\mathbb {U}_r}$ is a bundle in affine spaces, the compactly supported (geometric) cohomology groups of source and target are identified, equivariantly for the
$S_{\mathbb {T}_r,\mathbb {U}_r} \rightarrow Y_{\mathbb {T}_r,\mathbb {U}_r}$ is a bundle in affine spaces, the compactly supported (geometric) cohomology groups of source and target are identified, equivariantly for the ![]() $G_{x,0:r+} \times T_{x,0:r+}$-action, up to Tate twist and an (even) shift of cohomological degrees, so they will lead to the same (virtual) representations. The
$G_{x,0:r+} \times T_{x,0:r+}$-action, up to Tate twist and an (even) shift of cohomological degrees, so they will lead to the same (virtual) representations. The ![]() $Y_{\mathbb {T}_r, \mathbb {U}_r}$ are called ‘deep level Deligne–Lusztig varieties.’
$Y_{\mathbb {T}_r, \mathbb {U}_r}$ are called ‘deep level Deligne–Lusztig varieties.’
Example When ![]() $r=0$, the definition of
$r=0$, the definition of ![]() $Y_{\mathbb {T}_r,\mathbb {U}_r}$ specializes to that of a classical Deligne–Lusztig variety.
$Y_{\mathbb {T}_r,\mathbb {U}_r}$ specializes to that of a classical Deligne–Lusztig variety.
Definition 8.1 (Generalized Deligne–Lusztig induction)
Let ![]() $\Lambda \in \{\overline {\mathbb {F}}_{\ell }, \overline {\mathbb {Q}}_{\ell }, k, {\mathcal {O}}\}$ be an
$\Lambda \in \{\overline {\mathbb {F}}_{\ell }, \overline {\mathbb {Q}}_{\ell }, k, {\mathcal {O}}\}$ be an ![]() $\ell$-adic coefficient ring and
$\ell$-adic coefficient ring and ![]() $\theta \colon \mathbb {T}_r(\mathbb {F}_q) \rightarrow \Lambda ^{\times }$ be a character. We denote
$\theta \colon \mathbb {T}_r(\mathbb {F}_q) \rightarrow \Lambda ^{\times }$ be a character. We denote
which is a graded representation of ![]() $G_{x, 0:r+}$. We define the virtual representation of
$G_{x, 0:r+}$. We define the virtual representation of ![]() $G_{x, 0:r+x}$,
$G_{x, 0:r+x}$,
The version of this definition with ![]() $\Lambda = \overline {\mathbb {Q}}_{\ell }$ is considered in [Reference Chan and IvanovCI21, Definition 3.4], while we will also be interested in
$\Lambda = \overline {\mathbb {Q}}_{\ell }$ is considered in [Reference Chan and IvanovCI21, Definition 3.4], while we will also be interested in ![]() $\Lambda = \overline {\mathbb {F}}_{\ell }$.
$\Lambda = \overline {\mathbb {F}}_{\ell }$.
Remark 8.2 By inflation, we may view ![]() $\theta$ as a character of
$\theta$ as a character of ![]() $T_{x,0}$ that is trivial on
$T_{x,0}$ that is trivial on ![]() $T_{x,r+}$, and
$T_{x,r+}$, and ![]() $R^{\mathbb {G}_r}_{\mathbb {T}_r,\mathbb {U}_r}(\theta ) \in K_0(G_{x, 0}; \Lambda )$. In practice,
$R^{\mathbb {G}_r}_{\mathbb {T}_r,\mathbb {U}_r}(\theta ) \in K_0(G_{x, 0}; \Lambda )$. In practice, ![]() $\theta$ will come by restriction from a character of
$\theta$ will come by restriction from a character of ![]() $T(F)$.
$T(F)$.
Definition 8.3 Following [Reference Chan and IvanovCI21, § 2.10] in the case of ![]() $\overline {\mathbb {Q}}_{\ell }$-coefficients, we say that
$\overline {\mathbb {Q}}_{\ell }$-coefficients, we say that ![]() $\theta \colon \mathbb {T}_r(\mathbb {F}_q) \rightarrow k^{\times }$ is regular if for any absolute root
$\theta \colon \mathbb {T}_r(\mathbb {F}_q) \rightarrow k^{\times }$ is regular if for any absolute root ![]() $\alpha$ and any
$\alpha$ and any ![]() $d \geq 1$ such that
$d \geq 1$ such that ![]() $\operatorname {Fr}_q^d(\alpha ) = \alpha$, the restriction of
$\operatorname {Fr}_q^d(\alpha ) = \alpha$, the restriction of
to the subgroup (defined in [Reference Chan and IvanovCI21, § 2.6]) ![]() $\mathbb {T}_r^{\alpha, r} \subset \mathbb {T}_r(\mathbb {F}_{q^d})$ is non-trivial. Here
$\mathbb {T}_r^{\alpha, r} \subset \mathbb {T}_r(\mathbb {F}_{q^d})$ is non-trivial. Here ![]() $\operatorname {Nm}$ is the norm map sending
$\operatorname {Nm}$ is the norm map sending ![]() $t \mapsto t \cdot \sigma (t) \cdots \sigma ^{\ell -1}(t)$.
$t \mapsto t \cdot \sigma (t) \cdots \sigma ^{\ell -1}(t)$.
For a finite group ![]() $\Gamma$ and a virtual representation
$\Gamma$ and a virtual representation ![]() $V \in K_0(\Gamma ; \Lambda )$ which is a representation up to sign, we define
$V \in K_0(\Gamma ; \Lambda )$ which is a representation up to sign, we define ![]() $|V|$ to be the underlying representation and
$|V|$ to be the underlying representation and ![]() $(-1)^V$ to be the sign of
$(-1)^V$ to be the sign of ![]() $V$, so that
$V$, so that ![]() $V = (-1)^V |V|$.
$V = (-1)^V |V|$.
Lemma 8.4 Let ![]() $\Lambda \in \{ \overline {\mathbb {Q}}_{\ell }, \overline {\mathbb {F}}_{\ell }\}$.
$\Lambda \in \{ \overline {\mathbb {Q}}_{\ell }, \overline {\mathbb {F}}_{\ell }\}$.
(i) If
 $\theta$ is regular, then
$\theta$ is regular, then  $R^{\mathbb {G}_r}_{\mathbb {T}_r,\mathbb {U}_r}(\theta ) \in K_0(\mathbb {G}_r(\mathbb {F}_q); \Lambda )$ is independent of
$R^{\mathbb {G}_r}_{\mathbb {T}_r,\mathbb {U}_r}(\theta ) \in K_0(\mathbb {G}_r(\mathbb {F}_q); \Lambda )$ is independent of  $\mathbb {U}_r$.
$\mathbb {U}_r$.(ii) If
 $\theta$ is regular and the stabilizer of
$\theta$ is regular and the stabilizer of  $\theta$ in the Weyl group of the special fiber of
$\theta$ in the Weyl group of the special fiber of  ${\mathcal {G}}$ is trivial, then
${\mathcal {G}}$ is trivial, then  $\pm R_{\mathbb {T}_r,\mathbb {U}_r}^{\theta }$ is a (non-virtual) representation of
$\pm R_{\mathbb {T}_r,\mathbb {U}_r}^{\theta }$ is a (non-virtual) representation of  $G_{x,0:r+}$ and
$G_{x,0:r+}$ and  $|R_{\mathbb {T}_r,\mathbb {U}_r}^{\theta }|$ is irreducible.
$|R_{\mathbb {T}_r,\mathbb {U}_r}^{\theta }|$ is irreducible.
Proof. Both (i) and (ii) are established in [Reference Chan and IvanovCI21] when ![]() $\Lambda = \overline {\mathbb {Q}}_{\ell }$, so we shall simply explain the reduction from this case to
$\Lambda = \overline {\mathbb {Q}}_{\ell }$, so we shall simply explain the reduction from this case to ![]() $\Lambda = \overline {\mathbb {F}}_{\ell }$.
$\Lambda = \overline {\mathbb {F}}_{\ell }$.
(i) Any ![]() $\theta \colon T_{x,0:r+} \rightarrow \overline {\mathbb {F}}_{\ell }^{\times }$ lifts canonically to
$\theta \colon T_{x,0:r+} \rightarrow \overline {\mathbb {F}}_{\ell }^{\times }$ lifts canonically to ![]() $\widetilde {\theta } \colon T_{x,0:r+} \rightarrow \overline {\mathbb {Z}}_{\ell }^{\times } \subset \overline {\mathbb {Q}}_{\ell }^{\times }$ via the Teichmüller map. Moreover,
$\widetilde {\theta } \colon T_{x,0:r+} \rightarrow \overline {\mathbb {Z}}_{\ell }^{\times } \subset \overline {\mathbb {Q}}_{\ell }^{\times }$ via the Teichmüller map. Moreover, ![]() $R^{\mathbb {G}_r}_{\mathbb {T}_r,\mathbb {U}_r}(\theta )$ is the image of
$R^{\mathbb {G}_r}_{\mathbb {T}_r,\mathbb {U}_r}(\theta )$ is the image of ![]() $R^{\mathbb {G}_r}_{\mathbb {T}_r,\mathbb {U}_r}(\widetilde {\theta })$, the characteristic-zero Deligne–Lusztig induction studied in [Reference Chan and IvanovCI21, § 3.1], under the reduction map
$R^{\mathbb {G}_r}_{\mathbb {T}_r,\mathbb {U}_r}(\widetilde {\theta })$, the characteristic-zero Deligne–Lusztig induction studied in [Reference Chan and IvanovCI21, § 3.1], under the reduction map ![]() $K_0(G_{x,0:r+} ; \overline {\mathbb {Q}}_{\ell }) \rightarrow K_0(G_{x,0:r+}; \overline {\mathbb {F}}_{\ell })$. If
$K_0(G_{x,0:r+} ; \overline {\mathbb {Q}}_{\ell }) \rightarrow K_0(G_{x,0:r+}; \overline {\mathbb {F}}_{\ell })$. If ![]() $\theta$ is regular then
$\theta$ is regular then ![]() $\widetilde {\theta }$ is regular in the sense of [Reference Chan and IvanovCI21, § 2.10], so by [Reference Chan and IvanovCI21, Theorem 1.1(i)]
$\widetilde {\theta }$ is regular in the sense of [Reference Chan and IvanovCI21, § 2.10], so by [Reference Chan and IvanovCI21, Theorem 1.1(i)] ![]() $R^{\mathbb {G}_r}_{\mathbb {T}_r,\mathbb {U}_r}(\widetilde {\theta })$ is independent of
$R^{\mathbb {G}_r}_{\mathbb {T}_r,\mathbb {U}_r}(\widetilde {\theta })$ is independent of ![]() $U$.
$U$.
(ii) This follows from lifting to characteristic ![]() $0$ and a similar argument to that in (i), using [Reference Chan and IvanovCI21, Theorem 1.1(i)] for the analogous statement in characteristic
$0$ and a similar argument to that in (i), using [Reference Chan and IvanovCI21, Theorem 1.1(i)] for the analogous statement in characteristic ![]() $0$. We note that
$0$. We note that ![]() $|R_{\mathbb {T}_r,\mathbb {U}_r}^{\theta }|$ is non-zero by [Reference Chan and IvanovCI21, Corollary 4.3].
$|R_{\mathbb {T}_r,\mathbb {U}_r}^{\theta }|$ is non-zero by [Reference Chan and IvanovCI21, Corollary 4.3].
8.2 Tate cohomology of some generalized Deligne–Lusztig inductions
8.2.1 Recollections on Tate cohomology
Let ![]() $\sigma$ be an order-
$\sigma$ be an order-![]() $\ell$ endomorphism of an abelian group
$\ell$ endomorphism of an abelian group ![]() $V$. Write
$V$. Write ![]() $N := 1 + \sigma + \cdots + \sigma ^{\ell -1} \in \mathbb {Z}[\langle \sigma \rangle ]$. The Tate cohomology groups of
$N := 1 + \sigma + \cdots + \sigma ^{\ell -1} \in \mathbb {Z}[\langle \sigma \rangle ]$. The Tate cohomology groups of ![]() $V$ (with respect to the
$V$ (with respect to the ![]() $\sigma$-action) are defined as
$\sigma$-action) are defined as
 \begin{align*} \mathrm{T}^0 (\sigma, V) &= \mathrm{T}^0(V) := \frac{\ker( 1- \sigma \colon V \rightarrow V)}{N \cdot V},\\ \mathrm{T}^1 (\sigma, V) &= \mathrm{T}^1(V) := \frac{\ker(N \colon V \rightarrow V) }{(1-\sigma) \cdot V}. \end{align*}
\begin{align*} \mathrm{T}^0 (\sigma, V) &= \mathrm{T}^0(V) := \frac{\ker( 1- \sigma \colon V \rightarrow V)}{N \cdot V},\\ \mathrm{T}^1 (\sigma, V) &= \mathrm{T}^1(V) := \frac{\ker(N \colon V \rightarrow V) }{(1-\sigma) \cdot V}. \end{align*}
It is sometimes convenient to extend the definition of ![]() $T^i(V)$ 2-periodically to all
$T^i(V)$ 2-periodically to all ![]() $i \in \mathbb {Z}$, so that
$i \in \mathbb {Z}$, so that ![]() $T^i (-)= T^{i+2}(-)$.
$T^i (-)= T^{i+2}(-)$.
Given a short exact sequence
there is a (periodic) long exact sequence on Tate cohomology
In [Reference FengFen24, § 3.4], we defined the notion of Tate cohomology for a scheme ![]() $Y$ with an admissible action of
$Y$ with an admissible action of ![]() $\mathbb {Z}/\ell \mathbb {Z} \cong \langle \sigma \rangle$. Admissibility automatically holds if
$\mathbb {Z}/\ell \mathbb {Z} \cong \langle \sigma \rangle$. Admissibility automatically holds if ![]() $Y$ is a quasiprojective variety over a field, and we will always be in this situation when invoking this theory, so let us assume
$Y$ is a quasiprojective variety over a field, and we will always be in this situation when invoking this theory, so let us assume ![]() $Y$ is such. Another useful description of the (compactly supported) Tate cohomology group
$Y$ is such. Another useful description of the (compactly supported) Tate cohomology group ![]() $\mathrm {T}^i(\sigma, Y; \Lambda ) = \mathrm {T}^i(Y; \Lambda )$ with coefficients in
$\mathrm {T}^i(\sigma, Y; \Lambda ) = \mathrm {T}^i(Y; \Lambda )$ with coefficients in ![]() $\Lambda$ is the
$\Lambda$ is the ![]() $i$th cohomology of the totalization of
$i$th cohomology of the totalization of

It is immediate from this definition that ![]() $\mathrm {T}^i(-) \cong \mathrm {T}^{i+2}(-)$, so we sometimes treat
$\mathrm {T}^i(-) \cong \mathrm {T}^{i+2}(-)$, so we sometimes treat ![]() $\mathrm {T}^i$ as being defined for
$\mathrm {T}^i$ as being defined for ![]() $i \in \mathbb {Z}/2\mathbb {Z}$. We shall be interested in coefficients such as
$i \in \mathbb {Z}/2\mathbb {Z}$. We shall be interested in coefficients such as ![]() $\Lambda \in \{\overline {\mathbb {F}}_{\ell }, \overline {\mathbb {Z}}_{\ell }, k, {\mathcal {O}}, {\mathcal {O}}/\ell ^n\}$.
$\Lambda \in \{\overline {\mathbb {F}}_{\ell }, \overline {\mathbb {Z}}_{\ell }, k, {\mathcal {O}}, {\mathcal {O}}/\ell ^n\}$.
The double complex (8.2) leads to two spectral sequences abutting to ![]() $\mathrm {T}^*(Y; \overline {\mathbb {F}}_{\ell })$:
$\mathrm {T}^*(Y; \overline {\mathbb {F}}_{\ell })$:
• The ‘vertical then horizontal’ spectral sequence has first page
Its \[ E_1^{ij} = H^j_c(Y; \Lambda). \]
\[ E_1^{ij} = H^j_c(Y; \Lambda). \]
 $j$th row is the complex computing
$j$th row is the complex computing  $\mathrm {T}^i(H^j_c(Y; \Lambda ))$, namely,
Therefore, the second page is
$\mathrm {T}^i(H^j_c(Y; \Lambda ))$, namely,
Therefore, the second page is \[ \cdots \xrightarrow{N} H^j_c(Y; \Lambda) \xrightarrow{1-\sigma} H^j_c(Y; \Lambda) \xrightarrow{N} H^j_c(Y; \Lambda) \xrightarrow{1-\sigma} \cdots. \]
\[ \cdots \xrightarrow{N} H^j_c(Y; \Lambda) \xrightarrow{1-\sigma} H^j_c(Y; \Lambda) \xrightarrow{N} H^j_c(Y; \Lambda) \xrightarrow{1-\sigma} \cdots. \]
 \[ E_2^{ij} = \mathrm{T}^i(\sigma, H^j_c(Y; \Lambda)) . \]
\[ E_2^{ij} = \mathrm{T}^i(\sigma, H^j_c(Y; \Lambda)) . \]
• The ‘horizontal then vertical’ spectral sequence has
and, moreover, is degenerate starting from \[ E_2^{ij} = H^j_c(Y^{\sigma}; \Lambda) \]
\[ E_2^{ij} = H^j_c(Y^{\sigma}; \Lambda) \]
 $E_2$ [Reference Treumann and VenkateshTV16, Theorem 4.4].
$E_2$ [Reference Treumann and VenkateshTV16, Theorem 4.4].
8.2.2 Tate cohomology of representations
Let ![]() $V$ be a representation over
$V$ be a representation over ![]() $k$ of a finite group
$k$ of a finite group ![]() $\Gamma$. Suppose
$\Gamma$. Suppose ![]() $\mathbb {Z}/\ell \mathbb {Z} \cong \langle \sigma \rangle$ acts on
$\mathbb {Z}/\ell \mathbb {Z} \cong \langle \sigma \rangle$ acts on ![]() $\Gamma$. Then
$\Gamma$. Then ![]() $V \mapsto V \circ \sigma$ defines an action of
$V \mapsto V \circ \sigma$ defines an action of ![]() $\sigma$ on isomorphism classes of representations of
$\sigma$ on isomorphism classes of representations of ![]() $\Gamma$ over
$\Gamma$ over ![]() $\overline {\mathbb {F}}_{\ell }$.
$\overline {\mathbb {F}}_{\ell }$.
Lemma 8.5 If ![]() $V$ is irreducible and
$V$ is irreducible and ![]() $V \cong V \circ \sigma$ as
$V \cong V \circ \sigma$ as ![]() $\Gamma$-representations, then there is a unique extension of the
$\Gamma$-representations, then there is a unique extension of the ![]() $\Gamma$-action on
$\Gamma$-action on ![]() $V$ to an action of
$V$ to an action of ![]() $\Gamma \rtimes \langle \sigma \rangle$.
$\Gamma \rtimes \langle \sigma \rangle$.
Proof. If ![]() $A \colon V \xrightarrow {\sim } V \circ \sigma$ as
$A \colon V \xrightarrow {\sim } V \circ \sigma$ as ![]() $\Gamma$-representations, then Schur's lemma implies that the composition
$\Gamma$-representations, then Schur's lemma implies that the composition ![]() $A^\ell \colon V \xrightarrow {\sim } V \circ \sigma ^\ell = V$ is multiplication by a scalar, say
$A^\ell \colon V \xrightarrow {\sim } V \circ \sigma ^\ell = V$ is multiplication by a scalar, say ![]() $\lambda$. Then defining
$\lambda$. Then defining ![]() $\sigma$ to act as
$\sigma$ to act as ![]() $\lambda ^{-1/\ell } A$ gives an extension of the desired form. Schur's lemma also implies that
$\lambda ^{-1/\ell } A$ gives an extension of the desired form. Schur's lemma also implies that ![]() $A$ is unique up to scalar, and scaling
$A$ is unique up to scalar, and scaling ![]() $A$ evidently results in the same extension.
$A$ evidently results in the same extension.
For a ![]() $\mathbb {Z}/\ell \mathbb {Z} \cong \langle \sigma \rangle$-module
$\mathbb {Z}/\ell \mathbb {Z} \cong \langle \sigma \rangle$-module ![]() $V$, we have defined Tate cohomology groups
$V$, we have defined Tate cohomology groups ![]() $\mathrm {T}^0(V)$ and
$\mathrm {T}^0(V)$ and ![]() $\mathrm {T}^1(V)$. If the
$\mathrm {T}^1(V)$. If the ![]() $\sigma$-action on
$\sigma$-action on ![]() $V$ extends to an action of
$V$ extends to an action of ![]() $\Gamma \rtimes \langle \sigma \rangle$, then
$\Gamma \rtimes \langle \sigma \rangle$, then ![]() $\mathrm {T}^0(V)$ and
$\mathrm {T}^0(V)$ and ![]() $\mathrm {T}^1(V)$ inherit an action of the subgroup of
$\mathrm {T}^1(V)$ inherit an action of the subgroup of ![]() $\Gamma$ fixed by
$\Gamma$ fixed by ![]() $\sigma$, which we denote
$\sigma$, which we denote ![]() $Z_\Gamma (\sigma )$.
$Z_\Gamma (\sigma )$.
8.2.3 Torsion in integral cohomology
We write
for the decomposition into the torsion-free and torsion summands, respectively. For a character ![]() $\widetilde {\theta } \colon \mathbb {T}_r(\mathbb {F}_q) \rightarrow \overline {\mathbb {Z}}_{\ell }^{\times }$, we write
$\widetilde {\theta } \colon \mathbb {T}_r(\mathbb {F}_q) \rightarrow \overline {\mathbb {Z}}_{\ell }^{\times }$, we write
Thus ![]() $H_c^i(Y_{\mathbb {T}_r, \mathbb {U}_r}; \overline {\mathbb {Z}}_{\ell })_{\mathrm {tf}, \widetilde {\theta }}$ is a lattice in
$H_c^i(Y_{\mathbb {T}_r, \mathbb {U}_r}; \overline {\mathbb {Z}}_{\ell })_{\mathrm {tf}, \widetilde {\theta }}$ is a lattice in ![]() $H_c^i(Y_{\mathbb {T}_r, \mathbb {U}_r}; \overline {\mathbb {Q}}_{\ell })_{\widetilde {\theta }}$.
$H_c^i(Y_{\mathbb {T}_r, \mathbb {U}_r}; \overline {\mathbb {Q}}_{\ell })_{\widetilde {\theta }}$.
Write ![]() $\theta := \widetilde {\theta } \otimes _{\overline {\mathbb {Z}}_{\ell }} \overline {\mathbb {F}}_{\ell } \colon \mathbb {T}_r(\mathbb {F}_q) \rightarrow \overline {\mathbb {F}}_{\ell }^{\times }$. We consider the hypothesis that
$\theta := \widetilde {\theta } \otimes _{\overline {\mathbb {Z}}_{\ell }} \overline {\mathbb {F}}_{\ell } \colon \mathbb {T}_r(\mathbb {F}_q) \rightarrow \overline {\mathbb {F}}_{\ell }^{\times }$. We consider the hypothesis that
We will then be interested in studying ![]() $\mathrm {T}^i(\sigma, H_c^*(Y_{\mathbb {T}_r, \mathbb {U}_r}; \overline {\mathbb {F}}_{\ell })_{\theta })$ as a representation of
$\mathrm {T}^i(\sigma, H_c^*(Y_{\mathbb {T}_r, \mathbb {U}_r}; \overline {\mathbb {F}}_{\ell })_{\theta })$ as a representation of ![]() $G_{x, 0:r+}$, where
$G_{x, 0:r+}$, where ![]() $\sigma$ is a Galois automorphism (see § 8.2.4 below). For regular
$\sigma$ is a Galois automorphism (see § 8.2.4 below). For regular ![]() $\theta$, it is expected that
$\theta$, it is expected that ![]() $H_c^*(Y_{\mathbb {T}_r, \mathbb {U}_r}; \overline {\mathbb {Q}}_{\ell })_{\theta }$ is non-zero in only one degree. Therefore, if
$H_c^*(Y_{\mathbb {T}_r, \mathbb {U}_r}; \overline {\mathbb {Q}}_{\ell })_{\theta }$ is non-zero in only one degree. Therefore, if ![]() $\theta$ is regular and
$\theta$ is regular and ![]() $q$ is sufficiently large, then one would expect (8.3) to hold for all large enough
$q$ is sufficiently large, then one would expect (8.3) to hold for all large enough ![]() $\ell$, as a case of the more general expectation that for any (finite type) variety over a separably closed field, the étale cohomology with coefficients in
$\ell$, as a case of the more general expectation that for any (finite type) variety over a separably closed field, the étale cohomology with coefficients in ![]() $\mathbb {Z}_{\ell }$ should be torsion-free for all sufficiently large
$\mathbb {Z}_{\ell }$ should be torsion-free for all sufficiently large ![]() $\ell$; however, this does not appear to be known in general. When
$\ell$; however, this does not appear to be known in general. When ![]() $r=0$, in which case the
$r=0$, in which case the ![]() $Y_{\mathbb {T}_r, \mathbb {U}_r}$ are the usual Deligne–Lusztig varieties of [Reference Deligne and LusztigDL76], this concentration of degree and torsion-freeness for non-singular
$Y_{\mathbb {T}_r, \mathbb {U}_r}$ are the usual Deligne–Lusztig varieties of [Reference Deligne and LusztigDL76], this concentration of degree and torsion-freeness for non-singular ![]() $\theta$ is proved in [Reference BrouéBro90, Lemma 3.5] applied to the compactification of Deligne–Lusztig varieties, which already furnishes many interesting examples where (8.3) is known. Based on this, it seems natural to make the following conjecture.
$\theta$ is proved in [Reference BrouéBro90, Lemma 3.5] applied to the compactification of Deligne–Lusztig varieties, which already furnishes many interesting examples where (8.3) is known. Based on this, it seems natural to make the following conjecture.
Conjecture 8.6 If ![]() $\theta$ is a 0-toral character in the sense of [Reference Chan and OiCO23, Definition 3.7], then (8.3) holds.
$\theta$ is a 0-toral character in the sense of [Reference Chan and OiCO23, Definition 3.7], then (8.3) holds.
Later we will prove theorems concerning 0-toral ![]() $\theta$ under the assumption that (8.3) holds. It would be interesting to make these unconditional by proving Conjecture 8.6. As discussed, we already have many unconditional depth-zero examples.
$\theta$ under the assumption that (8.3) holds. It would be interesting to make these unconditional by proving Conjecture 8.6. As discussed, we already have many unconditional depth-zero examples.
Lemma 8.7 Suppose ![]() $\theta \colon \mathbb {T}_r(\mathbb {F}_q) \rightarrow \overline {\mathbb {F}}_{\ell }^{\times }$ satisfies (8.3) and let
$\theta \colon \mathbb {T}_r(\mathbb {F}_q) \rightarrow \overline {\mathbb {F}}_{\ell }^{\times }$ satisfies (8.3) and let ![]() $\widetilde {\theta } \colon \mathbb {T}_r(\mathbb {F}_q) \rightarrow \overline {\mathbb {Z}}_{\ell }^{\times }$ be the composition of
$\widetilde {\theta } \colon \mathbb {T}_r(\mathbb {F}_q) \rightarrow \overline {\mathbb {Z}}_{\ell }^{\times }$ be the composition of ![]() $\theta$ with the Teichmüller lift. Let
$\theta$ with the Teichmüller lift. Let ![]() $i$ be the unique degree in which
$i$ be the unique degree in which ![]() $H_c^i(Y_{\mathbb {T}_r, \mathbb {U}_r}; \overline {\mathbb {F}}_{\ell })_{\theta }$ is non-zero. Then
$H_c^i(Y_{\mathbb {T}_r, \mathbb {U}_r}; \overline {\mathbb {F}}_{\ell })_{\theta }$ is non-zero. Then ![]() $H_c^i(Y_{\mathbb {T}_r, \mathbb {U}_r}; \overline {\mathbb {Z}}_{\ell })_{\widetilde {\theta }}$ is a lattice in
$H_c^i(Y_{\mathbb {T}_r, \mathbb {U}_r}; \overline {\mathbb {Z}}_{\ell })_{\widetilde {\theta }}$ is a lattice in ![]() $H_c^i(Y_{\mathbb {T}_r, \mathbb {U}_r}; \overline {\mathbb {Q}}_{\ell })_{\widetilde {\theta }}$.
$H_c^i(Y_{\mathbb {T}_r, \mathbb {U}_r}; \overline {\mathbb {Q}}_{\ell })_{\widetilde {\theta }}$.
Proof. We must show that ![]() $H_c^i(Y_{\mathbb {T}_r, \mathbb {U}_r}; \overline {\mathbb {Z}}_{\ell })_{\widetilde {\theta }}$ is torsion-free. The universal coefficient theorem implies that
$H_c^i(Y_{\mathbb {T}_r, \mathbb {U}_r}; \overline {\mathbb {Z}}_{\ell })_{\widetilde {\theta }}$ is torsion-free. The universal coefficient theorem implies that ![]() $\big (H_c^i(Y_{\mathbb {T}_r, \mathbb {U}_r}; \overline {\mathbb {Z}}_{\ell })_{\widetilde {\theta }}\big )_{\operatorname {tors}} \otimes _{\overline {\mathbb {Z}}_{\ell }} \overline {\mathbb {F}}_{\ell }$ injects into
$\big (H_c^i(Y_{\mathbb {T}_r, \mathbb {U}_r}; \overline {\mathbb {Z}}_{\ell })_{\widetilde {\theta }}\big )_{\operatorname {tors}} \otimes _{\overline {\mathbb {Z}}_{\ell }} \overline {\mathbb {F}}_{\ell }$ injects into ![]() $H_c^{i+1}(Y_{\mathbb {T}_r, \mathbb {U}_r}; \overline {\mathbb {F}}_{\ell })_{\theta } = 0$, so
$H_c^{i+1}(Y_{\mathbb {T}_r, \mathbb {U}_r}; \overline {\mathbb {F}}_{\ell })_{\theta } = 0$, so ![]() $\big (H_c^i(Y_{\mathbb {T}_r, \mathbb {U}_r}; \overline {\mathbb {Z}}_{\ell })_{\widetilde {\theta }}\big )_{\operatorname {tors}} = 0$ by Nakayama's lemma.
$\big (H_c^i(Y_{\mathbb {T}_r, \mathbb {U}_r}; \overline {\mathbb {Z}}_{\ell })_{\widetilde {\theta }}\big )_{\operatorname {tors}} = 0$ by Nakayama's lemma.
8.2.4 Base change
Recall that ![]() $F_{\ell }$ is the degree-
$F_{\ell }$ is the degree-![]() $\ell$ unramified extension of
$\ell$ unramified extension of ![]() $F$. Let
$F$. Let ![]() $T' = \operatorname {Res}_{F_{\ell }/F} (T_{F_\ell })$,
$T' = \operatorname {Res}_{F_{\ell }/F} (T_{F_\ell })$, ![]() $G' = \operatorname {Res}_{F_{\ell }/F}(G_{F_\ell })$. We may view
$G' = \operatorname {Res}_{F_{\ell }/F}(G_{F_\ell })$. We may view ![]() $x$ as a point in the apartment of
$x$ as a point in the apartment of ![]() $T'$, in the building of
$T'$, in the building of ![]() $G'/F$.
$G'/F$.
Given ![]() $U \subset G_{\breve {F}}$, we have several possible choices for
$U \subset G_{\breve {F}}$, we have several possible choices for ![]() $U' \subset G'_{\breve {F}}$. We will make a particular choice that is advantageous for the upcoming computation. A choice of generator
$U' \subset G'_{\breve {F}}$. We will make a particular choice that is advantageous for the upcoming computation. A choice of generator ![]() $\sigma \in \operatorname {Gal}(F_{\ell }/F)$ induces an isomorphism
$\sigma \in \operatorname {Gal}(F_{\ell }/F)$ induces an isomorphism
sending ![]() $x \otimes y \mapsto (xy, \sigma (x)y, \ldots, \sigma ^{\ell -1}(x) y)$. This in turn induces
$x \otimes y \mapsto (xy, \sigma (x)y, \ldots, \sigma ^{\ell -1}(x) y)$. This in turn induces
The action of ![]() $\sigma$ on the left-hand side transports to the cyclic permutation on the right-hand side. We define
$\sigma$ on the left-hand side transports to the cyclic permutation on the right-hand side. We define ![]() $U' \subset G'_{\breve {F}}$ to be the image of
$U' \subset G'_{\breve {F}}$ to be the image of ![]() $U \times \cdots \times U \subset G_{\breve {F}}^{\ell }$ under the isomorphism (8.4). Then
$U \times \cdots \times U \subset G_{\breve {F}}^{\ell }$ under the isomorphism (8.4). Then ![]() $U'$ is stable under the
$U'$ is stable under the ![]() $\sigma$-action on
$\sigma$-action on ![]() $G'_{\breve {F}}$. The resulting deep level Deligne–Lusztig variety
$G'_{\breve {F}}$. The resulting deep level Deligne–Lusztig variety ![]() $Y_{\mathbb {T}_r', \mathbb {U}_r'}$ therefore carries an action of
$Y_{\mathbb {T}_r', \mathbb {U}_r'}$ therefore carries an action of ![]() $\sigma$, such that for
$\sigma$, such that for ![]() $g \in G'_{x, 0:r+} = \mathbb {G}_r'(\mathbb {F}_q)$ and
$g \in G'_{x, 0:r+} = \mathbb {G}_r'(\mathbb {F}_q)$ and ![]() $y \in Y_{\mathbb {T}_r', \mathbb {U}_r'}(R)$ (for some ring
$y \in Y_{\mathbb {T}_r', \mathbb {U}_r'}(R)$ (for some ring ![]() $R$),
$R$),
and similarly for ![]() $t \in T'_{x,0:r+} = \mathbb {T}_r'(\mathbb {F}_q)$. This induces a
$t \in T'_{x,0:r+} = \mathbb {T}_r'(\mathbb {F}_q)$. This induces a ![]() $\sigma$-action on
$\sigma$-action on ![]() $H_c^i(Y_{\mathbb {T}_r', \mathbb {U}_r'}; \overline {\mathbb {F}}_{\ell })$ that is compatible in the same manner with the
$H_c^i(Y_{\mathbb {T}_r', \mathbb {U}_r'}; \overline {\mathbb {F}}_{\ell })$ that is compatible in the same manner with the ![]() $\mathbb {G}'_r(\mathbb {F}_q) \times \mathbb {T}_r'(\mathbb {F}_q)$-action. We will consider Tate cohomology with respect to this action.
$\mathbb {G}'_r(\mathbb {F}_q) \times \mathbb {T}_r'(\mathbb {F}_q)$-action. We will consider Tate cohomology with respect to this action.
Recall that for a representation ![]() $V / \overline {\mathbb {F}}_{\ell }$ of a finite group
$V / \overline {\mathbb {F}}_{\ell }$ of a finite group ![]() $\Gamma$, the Frobenius twist of
$\Gamma$, the Frobenius twist of ![]() $V$ is the representation
$V$ is the representation
Now note that ![]() $H_c^i(Y_{\mathbb {T}_r, \mathbb {U}_r}; \overline {\mathbb {F}}_{\ell })$ has an
$H_c^i(Y_{\mathbb {T}_r, \mathbb {U}_r}; \overline {\mathbb {F}}_{\ell })$ has an ![]() $\mathbb {F}_{\ell }$-structure induced by cohomology with coefficients in
$\mathbb {F}_{\ell }$-structure induced by cohomology with coefficients in ![]() $\mathbb {F}_{\ell }$, and therefore has an action of
$\mathbb {F}_{\ell }$, and therefore has an action of ![]() $\operatorname {Aut}(\overline {\mathbb {F}}_{\ell })$. Let
$\operatorname {Aut}(\overline {\mathbb {F}}_{\ell })$. Let ![]() $\theta \colon T_{x, 0:r+} = \mathbb {T}_r(\mathbb {F}_q) \rightarrow \overline {\mathbb {F}}_{\ell }^{\times }$ be a character and
$\theta \colon T_{x, 0:r+} = \mathbb {T}_r(\mathbb {F}_q) \rightarrow \overline {\mathbb {F}}_{\ell }^{\times }$ be a character and ![]() $\theta ' \colon \mathbb {T}_r'(\mathbb {F}_q) \rightarrow \overline {\mathbb {F}}_{\ell }^{\times }$ be the composition of
$\theta ' \colon \mathbb {T}_r'(\mathbb {F}_q) \rightarrow \overline {\mathbb {F}}_{\ell }^{\times }$ be the composition of ![]() $\theta$ with the norm map
$\theta$ with the norm map ![]() $\operatorname {Nm} \colon \mathbb {T}_r'(\mathbb {F}_q) \rightarrow \mathbb {T}_r(\mathbb {F}_q)$. Applying
$\operatorname {Nm} \colon \mathbb {T}_r'(\mathbb {F}_q) \rightarrow \mathbb {T}_r(\mathbb {F}_q)$. Applying ![]() $\operatorname {Frob}_{\ell } \in \operatorname {Aut}(\overline {\mathbb {F}}_{\ell })$ induces an isomorphism of
$\operatorname {Frob}_{\ell } \in \operatorname {Aut}(\overline {\mathbb {F}}_{\ell })$ induces an isomorphism of ![]() $\mathbb {G}_r(\mathbb {F}_q)$-representations
$\mathbb {G}_r(\mathbb {F}_q)$-representations
Theorem 8.8 Let ![]() $\theta \colon \mathbb {T}_r(\mathbb {F}_q) \rightarrow \overline {\mathbb {F}}_{\ell }^{\times }$. Assume that
$\theta \colon \mathbb {T}_r(\mathbb {F}_q) \rightarrow \overline {\mathbb {F}}_{\ell }^{\times }$. Assume that ![]() $\ell \nmid \# \mathbb {T}_0(\mathbb {F}_q)$.
$\ell \nmid \# \mathbb {T}_0(\mathbb {F}_q)$.
(i) If
 $H^*_c(Y_{\mathbb {T}_r, \mathbb {U}_r};\overline {\mathbb {F}}_{\ell })_{\theta } \neq 0$, then
$H^*_c(Y_{\mathbb {T}_r, \mathbb {U}_r};\overline {\mathbb {F}}_{\ell })_{\theta } \neq 0$, then  $\mathrm {T}^i(\sigma, H_c^{i'}(Y_{\mathbb {T}_r', \mathbb {U}_r'};\overline {\mathbb {F}}_{\ell })_{\theta '}) \neq 0$ for some
$\mathrm {T}^i(\sigma, H_c^{i'}(Y_{\mathbb {T}_r', \mathbb {U}_r'};\overline {\mathbb {F}}_{\ell })_{\theta '}) \neq 0$ for some  $i \in \{0,1\}$ and some
$i \in \{0,1\}$ and some  $i'$.
$i'$.(ii) Suppose that
 $\theta$ and
$\theta$ and  $\theta '$ both satisfy (8.3), and are non-zero in degrees
$\theta '$ both satisfy (8.3), and are non-zero in degrees  $j,j'$, respectively. Then for each
$j,j'$, respectively. Then for each  $i \in \mathbb {Z}/2\mathbb {Z}$ we have
as representations of
$i \in \mathbb {Z}/2\mathbb {Z}$ we have
as representations of \[ \mathrm{T}^i \big(\sigma, H_c^{j'}(Y_{\mathbb{T}_r', \mathbb{U}_r'}; \overline{\mathbb{F}}_{\ell})_{\theta'} \otimes_{\overline{\mathbb{Z}}_{\ell}} \overline{\mathbb{F}}_{\ell} \big) \cong (H^j_c(Y_{\mathbb{T}_r, \mathbb{U}_r, F};\overline{\mathbb{F}}_{\ell})_{\theta})^{(\ell)} \]
\[ \mathrm{T}^i \big(\sigma, H_c^{j'}(Y_{\mathbb{T}_r', \mathbb{U}_r'}; \overline{\mathbb{F}}_{\ell})_{\theta'} \otimes_{\overline{\mathbb{Z}}_{\ell}} \overline{\mathbb{F}}_{\ell} \big) \cong (H^j_c(Y_{\mathbb{T}_r, \mathbb{U}_r, F};\overline{\mathbb{F}}_{\ell})_{\theta})^{(\ell)} \]
 $\mathbb {G}_r(\mathbb {F}_q)$. In particular, the left-hand side is independent of
$\mathbb {G}_r(\mathbb {F}_q)$. In particular, the left-hand side is independent of  $i$.
$i$.
Proof. We begin with some analysis of the relevant varieties. For a scheme ![]() $Y$ over
$Y$ over ![]() $\mathbb {F}_q$ we will write
$\mathbb {F}_q$ we will write ![]() $\overline {Y}$ for its base change to
$\overline {Y}$ for its base change to ![]() $\overline {\mathbb {F}}_q$.
$\overline {\mathbb {F}}_q$.
Parallel to (8.4), the choice of generator ![]() $\sigma \in \operatorname {Gal}(\mathbb {F}_{q^\ell }/\mathbb {F}_q)$ identifies
$\sigma \in \operatorname {Gal}(\mathbb {F}_{q^\ell }/\mathbb {F}_q)$ identifies
The isomorphism (8.6) transports:
• the automorphism
 $\sigma$ on the left-hand side to the cyclic rotation action on the right-hand side;
$\sigma$ on the left-hand side to the cyclic rotation action on the right-hand side;• the action of
 $\operatorname {Fr}_q$ on the left-hand side (coming from the
$\operatorname {Fr}_q$ on the left-hand side (coming from the  $\mathbb {F}_q$-rational structure
$\mathbb {F}_q$-rational structure  $\mathbb {G}'_r$ for
$\mathbb {G}'_r$ for  $\overline {\mathbb {G}}'_r$) to the composition of the cyclic rotation with
$\overline {\mathbb {G}}'_r$) to the composition of the cyclic rotation with  $(\operatorname {Fr}_q, \ldots, \operatorname {Fr}_q)$ on the right-hand side, where each factor of
$(\operatorname {Fr}_q, \ldots, \operatorname {Fr}_q)$ on the right-hand side, where each factor of  $\operatorname {Fr}_q$ comes from the
$\operatorname {Fr}_q$ comes from the  $\mathbb {F}_q$-rational structure
$\mathbb {F}_q$-rational structure  $\mathbb {G}_r$ on
$\mathbb {G}_r$ on  $\overline {\mathbb {G}}_r$. Let us denote this endomorphism of
$\overline {\mathbb {G}}_r$. Let us denote this endomorphism of  $\overline {\mathbb {G}}_r^{\ell }$ by
$\overline {\mathbb {G}}_r^{\ell }$ by  $F := \sigma \circ (\operatorname {Fr}_q, \ldots, \operatorname {Fr}_q)$.
$F := \sigma \circ (\operatorname {Fr}_q, \ldots, \operatorname {Fr}_q)$.
Similar remarks apply to ![]() $\mathbb {T}'_r \cong \operatorname {Res}_{\mathbb {F}_{q^\ell }/\mathbb {F}_q} (\mathbb {T}_{r, \mathbb {F}_{q^{\ell }}})$.
$\mathbb {T}'_r \cong \operatorname {Res}_{\mathbb {F}_{q^\ell }/\mathbb {F}_q} (\mathbb {T}_{r, \mathbb {F}_{q^{\ell }}})$.
Under (8.6), the variety ![]() $Y_{\mathbb {T}_r', \mathbb {U}_r'}$ has the presentation
$Y_{\mathbb {T}_r', \mathbb {U}_r'}$ has the presentation
The action of ![]() $\sigma$ on
$\sigma$ on ![]() $Y_{\mathbb {T}_r', \mathbb {U}_r'}$ transports to the cyclic rotation on factors in the presentation on the right-hand side.
$Y_{\mathbb {T}_r', \mathbb {U}_r'}$ transports to the cyclic rotation on factors in the presentation on the right-hand side.
Lemma 8.9 The diagonal map ![]() $Y_{\mathbb {T}_r, \mathbb {U}_r} \rightarrow Y_{\mathbb {T}_r', \mathbb {U}_r'}$ identifies with the inclusion of the
$Y_{\mathbb {T}_r, \mathbb {U}_r} \rightarrow Y_{\mathbb {T}_r', \mathbb {U}_r'}$ identifies with the inclusion of the ![]() $\sigma$-fixed points on
$\sigma$-fixed points on ![]() $Y_{\mathbb {T}_r', \mathbb {U}_r'}$, equivariantly for the action of
$Y_{\mathbb {T}_r', \mathbb {U}_r'}$, equivariantly for the action of ![]() $\mathbb {G}_r(\mathbb {F}_q) \times \mathbb {T}_r(\mathbb {F}_q)$ by left and right translation.
$\mathbb {G}_r(\mathbb {F}_q) \times \mathbb {T}_r(\mathbb {F}_q)$ by left and right translation.
Proof. Immediate upon writing down the definitions.
Corollary 8.10 For each ![]() $i \in \mathbb {Z}$, restriction induces an isomorphism
$i \in \mathbb {Z}$, restriction induces an isomorphism
which is equivariant with respect to the action of ![]() $Z_{\mathbb {G}_r'(\mathbb {F}_q) \times \mathbb {T}_r'(\mathbb {F}_q)}(\sigma ) = \mathbb {G}_r(\mathbb {F}_q) \times \mathbb {T}_r(\mathbb {F}_q)$, induced by left and right translation on
$Z_{\mathbb {G}_r'(\mathbb {F}_q) \times \mathbb {T}_r'(\mathbb {F}_q)}(\sigma ) = \mathbb {G}_r(\mathbb {F}_q) \times \mathbb {T}_r(\mathbb {F}_q)$, induced by left and right translation on ![]() $Y_{\mathbb {T}_r' , \mathbb {U}_r'}$ and
$Y_{\mathbb {T}_r' , \mathbb {U}_r'}$ and ![]() $Y_{\mathbb {T}_r, \mathbb {U}_r}$.
$Y_{\mathbb {T}_r, \mathbb {U}_r}$.
Proof. This follows from Lemma 8.9 and the equivariant localization theorem of [Reference FengFen24, § 3.4.5].
With these preparations, we are now ready for the proofs of parts (i) and (ii) of the theorem.
Proof of (i). Restricting ![]() $\theta '$ along
$\theta '$ along ![]() $\mathbb {T}_r(\mathbb {F}_q) \hookrightarrow \mathbb {T}_r'(\mathbb {F}_q)$ yields
$\mathbb {T}_r(\mathbb {F}_q) \hookrightarrow \mathbb {T}_r'(\mathbb {F}_q)$ yields ![]() $\theta '|_{\mathbb {T}_r(\mathbb {F}_q)} = \theta ^{\otimes \ell }$, so Corollary 8.10 induces an isomorphism of
$\theta '|_{\mathbb {T}_r(\mathbb {F}_q)} = \theta ^{\otimes \ell }$, so Corollary 8.10 induces an isomorphism of ![]() $\mathbb {G}_r(\mathbb {F}_q)$-representations
$\mathbb {G}_r(\mathbb {F}_q)$-representations
Similarly to (8.5), we have
Note that Frobenius twisting shows that ![]() $H^*_c(Y_{\mathbb {T}_r, \mathbb {U}_r};\overline {\mathbb {F}}_{\ell })_{\theta } \neq 0 \iff H^*_c(Y_{\mathbb {T}_r, \mathbb {U}_r};\overline {\mathbb {F}}_{\ell })_{\theta ^{\otimes \ell }} \neq 0$.
$H^*_c(Y_{\mathbb {T}_r, \mathbb {U}_r};\overline {\mathbb {F}}_{\ell })_{\theta } \neq 0 \iff H^*_c(Y_{\mathbb {T}_r, \mathbb {U}_r};\overline {\mathbb {F}}_{\ell })_{\theta ^{\otimes \ell }} \neq 0$.
As explained in § 8.2.2, there are two spectral sequences abutting to ![]() $\mathrm {T}^i(Y_{\mathbb {T}'_r, \mathbb {U}_r'}; \overline {\mathbb {F}}_{\ell })$. One degenerates at
$\mathrm {T}^i(Y_{\mathbb {T}'_r, \mathbb {U}_r'}; \overline {\mathbb {F}}_{\ell })$. One degenerates at ![]() $E_2$ and has
$E_2$ and has ![]() $E_2^{ij} = H^j_c((Y_{\mathbb {T}'_r, \mathbb {U}_r'})^{\sigma }; \overline {\mathbb {F}}_{\ell })$, which by Lemma 8.9 is
$E_2^{ij} = H^j_c((Y_{\mathbb {T}'_r, \mathbb {U}_r'})^{\sigma }; \overline {\mathbb {F}}_{\ell })$, which by Lemma 8.9 is ![]() $\mathbb {G}_r(\mathbb {F}_q) \times \mathbb {T}_r(\mathbb {F}_q)$-equivariantly isomorphic to
$\mathbb {G}_r(\mathbb {F}_q) \times \mathbb {T}_r(\mathbb {F}_q)$-equivariantly isomorphic to ![]() $H^j_c(Y_{\mathbb {T}_r, \mathbb {U}_r}; \overline {\mathbb {F}}_{\ell })$, and the other has
$H^j_c(Y_{\mathbb {T}_r, \mathbb {U}_r}; \overline {\mathbb {F}}_{\ell })$, and the other has ![]() $E_2^{ij} = \mathrm {T}^i (\sigma, H^j_c(Y_{\mathbb {T}'_r, \mathbb {U}_r'}; \overline {\mathbb {F}}_{\ell }))$.
$E_2^{ij} = \mathrm {T}^i (\sigma, H^j_c(Y_{\mathbb {T}'_r, \mathbb {U}_r'}; \overline {\mathbb {F}}_{\ell }))$.
Since ![]() $\ker (\mathbb {T}_r(\mathbb {F}_q) \rightarrow \mathbb {T}_0(\mathbb {F}_q))$ is pro-
$\ker (\mathbb {T}_r(\mathbb {F}_q) \rightarrow \mathbb {T}_0(\mathbb {F}_q))$ is pro-![]() $p$, the assumption that
$p$, the assumption that ![]() $\ell \nmid \mathbb {T}_0(\mathbb {F}_q)$ implies that
$\ell \nmid \mathbb {T}_0(\mathbb {F}_q)$ implies that ![]() $\ell \nmid \mathbb {T}_r(\mathbb {F}_q)$. Therefore,
$\ell \nmid \mathbb {T}_r(\mathbb {F}_q)$. Therefore, ![]() $- \otimes _{ \overline {\mathbb {F}}_{\ell }[\mathbb {T}_r(\mathbb {F}_q)]} \theta$ implements projection to a summand. By the preceding paragraph, the Jordan–Hölder factors (as
$- \otimes _{ \overline {\mathbb {F}}_{\ell }[\mathbb {T}_r(\mathbb {F}_q)]} \theta$ implements projection to a summand. By the preceding paragraph, the Jordan–Hölder factors (as ![]() $\mathbb {G}_r(\mathbb {F}_q)$-representations) of
$\mathbb {G}_r(\mathbb {F}_q)$-representations) of ![]() $H^j_c(Y_{\mathbb {T}_r, \mathbb {U}_r}; \overline {\mathbb {F}}_{\ell })_{\theta ^{\otimes \ell }}$ are also subquotients of some
$H^j_c(Y_{\mathbb {T}_r, \mathbb {U}_r}; \overline {\mathbb {F}}_{\ell })_{\theta ^{\otimes \ell }}$ are also subquotients of some ![]() $\mathrm {T}^i (H^{j'}_c(Y_{\mathbb {T}'_r, \mathbb {U}_r'}; \overline {\mathbb {F}}_{\ell })) \otimes _{ \overline {\mathbb {F}}_{\ell }[\mathbb {T}_r(\mathbb {F}_q)]} \theta ^{\otimes \ell }$. Therefore the proof of (i) will be concluded by the following lemma, which allows us to ‘commute’ the formation of Tate cohomology with the projection to an isotypic component.
$\mathrm {T}^i (H^{j'}_c(Y_{\mathbb {T}'_r, \mathbb {U}_r'}; \overline {\mathbb {F}}_{\ell })) \otimes _{ \overline {\mathbb {F}}_{\ell }[\mathbb {T}_r(\mathbb {F}_q)]} \theta ^{\otimes \ell }$. Therefore the proof of (i) will be concluded by the following lemma, which allows us to ‘commute’ the formation of Tate cohomology with the projection to an isotypic component.
Lemma 8.11 We have that
as ![]() $\mathbb {G}_r(\mathbb {F}_q)$-representations.
$\mathbb {G}_r(\mathbb {F}_q)$-representations.
Proof. Since ![]() $\# \mathbb {T}_r(\mathbb {F}_q)$ is coprime to
$\# \mathbb {T}_r(\mathbb {F}_q)$ is coprime to ![]() $\ell$, we have that
$\ell$, we have that
as ![]() $\mathbb {G}_r(\mathbb {F}_q)$-representations. Here on the right-hand side we have projected to a
$\mathbb {G}_r(\mathbb {F}_q)$-representations. Here on the right-hand side we have projected to a ![]() $\mathbb {T}_r(\mathbb {F}_q)$-isotypic component before forming Tate cohomology, and we need to show that the same answer is computed if we instead project to a particular
$\mathbb {T}_r(\mathbb {F}_q)$-isotypic component before forming Tate cohomology, and we need to show that the same answer is computed if we instead project to a particular ![]() $\mathbb {T}_r'(\mathbb {F}_q)$-isotypic component.
$\mathbb {T}_r'(\mathbb {F}_q)$-isotypic component.
Let ![]() $\{ \vartheta _l \}$ be the set of characters of
$\{ \vartheta _l \}$ be the set of characters of ![]() $\mathbb {T}_r'(\mathbb {F}_q)$ that extend
$\mathbb {T}_r'(\mathbb {F}_q)$ that extend ![]() $\theta ^{\otimes \ell }$ on
$\theta ^{\otimes \ell }$ on ![]() $\mathbb {T}_r(\mathbb {F}_q) \subset \mathbb {T}_r'(\mathbb {F}_q)$, indexed so that
$\mathbb {T}_r(\mathbb {F}_q) \subset \mathbb {T}_r'(\mathbb {F}_q)$, indexed so that ![]() $\vartheta _1 = \theta '$. Then
$\vartheta _1 = \theta '$. Then
 \begin{equation} \mathrm{T}^i \big(H^{j'}_c(Y_{\mathbb{T}'_r, \mathbb{U}_r'}; \overline{\mathbb{F}}_{\ell})\otimes_{ \overline{\mathbb{F}}_{\ell}[\mathbb{T}_r(\mathbb{F}_q)]} \theta^{\otimes \ell} \big) \cong \mathrm{T}^i \bigg( \bigoplus_l H^{j'}_c(Y_{\mathbb{T}'_r, \mathbb{U}_r'}; \overline{\mathbb{F}}_{\ell})\otimes_{ \overline{\mathbb{F}}_{\ell}[\mathbb{T}_r'(\mathbb{F}_q)]} \vartheta_l \bigg). \end{equation}
\begin{equation} \mathrm{T}^i \big(H^{j'}_c(Y_{\mathbb{T}'_r, \mathbb{U}_r'}; \overline{\mathbb{F}}_{\ell})\otimes_{ \overline{\mathbb{F}}_{\ell}[\mathbb{T}_r(\mathbb{F}_q)]} \theta^{\otimes \ell} \big) \cong \mathrm{T}^i \bigg( \bigoplus_l H^{j'}_c(Y_{\mathbb{T}'_r, \mathbb{U}_r'}; \overline{\mathbb{F}}_{\ell})\otimes_{ \overline{\mathbb{F}}_{\ell}[\mathbb{T}_r'(\mathbb{F}_q)]} \vartheta_l \bigg). \end{equation} We claim that ![]() $\theta '$ is the only
$\theta '$ is the only ![]() $\sigma$-equivariant extension of
$\sigma$-equivariant extension of ![]() $\theta ^{\otimes \ell }$ to
$\theta ^{\otimes \ell }$ to ![]() $\mathbb {T}_r'(\mathbb {F}_q)$. Indeed, any
$\mathbb {T}_r'(\mathbb {F}_q)$. Indeed, any ![]() $\sigma$-equivariant character on
$\sigma$-equivariant character on ![]() $\mathbb {T}_r'(\mathbb {F}_q)$ factors through the norm mapFootnote 8
$\mathbb {T}_r'(\mathbb {F}_q)$ factors through the norm mapFootnote 8 ![]() $\mathbb {T}_r'(\mathbb {F}_q) \xrightarrow {\operatorname {Nm}} \mathbb {T}_r(\mathbb {F}_q)$, and the composition
$\mathbb {T}_r'(\mathbb {F}_q) \xrightarrow {\operatorname {Nm}} \mathbb {T}_r(\mathbb {F}_q)$, and the composition ![]() $\mathbb {T}_r(\mathbb {F}_q) \hookrightarrow \mathbb {T}_r'(\mathbb {F}_q) \xrightarrow {\operatorname {Nm}} \mathbb {T}_r(\mathbb {F}_q)$ is raising to the
$\mathbb {T}_r(\mathbb {F}_q) \hookrightarrow \mathbb {T}_r'(\mathbb {F}_q) \xrightarrow {\operatorname {Nm}} \mathbb {T}_r(\mathbb {F}_q)$ is raising to the ![]() $\ell$th power. Since
$\ell$th power. Since ![]() $\overline {\mathbb {F}}_{\ell }^{\times }$ is
$\overline {\mathbb {F}}_{\ell }^{\times }$ is ![]() $\ell$-torsion-free, there is only one character
$\ell$-torsion-free, there is only one character ![]() $\mathbb {T}_r(\mathbb {F}_q) \rightarrow \overline {\mathbb {F}}_{\ell }^{\times }$ that inflates to
$\mathbb {T}_r(\mathbb {F}_q) \rightarrow \overline {\mathbb {F}}_{\ell }^{\times }$ that inflates to ![]() $\theta ^{\otimes \ell }$ under raising to the
$\theta ^{\otimes \ell }$ under raising to the ![]() $\ell$th power, namely
$\ell$th power, namely ![]() $\theta$.
$\theta$.
Therefore, ![]() $\sigma$ permutes the set
$\sigma$ permutes the set ![]() $\{\vartheta _l \colon l>1\}$ without any fixed points, necessarily grouping them into free orbits, and it therefore freely permutes the summands of
$\{\vartheta _l \colon l>1\}$ without any fixed points, necessarily grouping them into free orbits, and it therefore freely permutes the summands of
Since Tate cohomology of a free ![]() $\sigma$-module vanishes,
$\sigma$-module vanishes,
 \[ \mathrm{T}^i \bigg( \bigoplus_{l>1} H^{j'}_c(Y_{\mathbb{T}'_r, \mathbb{U}_r'}; \overline{\mathbb{F}}_{\ell})\otimes_{ \overline{\mathbb{F}}_{\ell}[\mathbb{T}_r'(\mathbb{F}_q)]} \vartheta_l\bigg) = 0. \]
\[ \mathrm{T}^i \bigg( \bigoplus_{l>1} H^{j'}_c(Y_{\mathbb{T}'_r, \mathbb{U}_r'}; \overline{\mathbb{F}}_{\ell})\otimes_{ \overline{\mathbb{F}}_{\ell}[\mathbb{T}_r'(\mathbb{F}_q)]} \vartheta_l\bigg) = 0. \]
Therefore, (8.8) is ![]() $\mathbb {G}_r(\mathbb {F}_q)$-equivariantly isomorphic to
$\mathbb {G}_r(\mathbb {F}_q)$-equivariantly isomorphic to ![]() $\mathrm {T}^i (H^{j'}_c(Y_{\mathbb {T}'_r, \mathbb {U}_r'}; \overline {\mathbb {F}}_{\ell })_{\theta '})$.
$\mathrm {T}^i (H^{j'}_c(Y_{\mathbb {T}'_r, \mathbb {U}_r'}; \overline {\mathbb {F}}_{\ell })_{\theta '})$.
Proof of (ii). We consider the Tate spectral sequence, as in part (i). The additional assumptions imply that:
•
 $R\Gamma _c(Y_{\mathbb {T}_r', \mathbb {U}_r'}; \overline {\mathbb {F}}_{\ell })_{\theta '}$ is concentrated in a single degree
$R\Gamma _c(Y_{\mathbb {T}_r', \mathbb {U}_r'}; \overline {\mathbb {F}}_{\ell })_{\theta '}$ is concentrated in a single degree  $j'$, and so is quasi-isomorphic to
$j'$, and so is quasi-isomorphic to  $H_c^{j'}(Y_{\mathbb {T}_r', \mathbb {U}_r'}; \overline {\mathbb {F}}_{\ell })_{\theta '}$;
$H_c^{j'}(Y_{\mathbb {T}_r', \mathbb {U}_r'}; \overline {\mathbb {F}}_{\ell })_{\theta '}$;•
 $R\Gamma _c(Y_{\mathbb {T}_r, \mathbb {U}_r}; \overline {\mathbb {F}}_{\ell })_{\theta }$ is concentrated in a single degree
$R\Gamma _c(Y_{\mathbb {T}_r, \mathbb {U}_r}; \overline {\mathbb {F}}_{\ell })_{\theta }$ is concentrated in a single degree  $j$, and so is quasi-isomorphic to
$j$, and so is quasi-isomorphic to  $H_c^{j}(Y_{\mathbb {T}_r, \mathbb {U}_r}; \overline {\mathbb {F}}_{\ell })_{\theta }$.
$H_c^{j}(Y_{\mathbb {T}_r, \mathbb {U}_r}; \overline {\mathbb {F}}_{\ell })_{\theta }$.
Corollary 8.10 then implies that
as ![]() $\mathbb {G}_r(\mathbb {F}_q) \times \mathbb {T}_r(\mathbb {F}_q)$-representations. Using Lemma 8.11, we find that
$\mathbb {G}_r(\mathbb {F}_q) \times \mathbb {T}_r(\mathbb {F}_q)$-representations. Using Lemma 8.11, we find that
as ![]() $\mathbb {G}_r(\mathbb {F}_q)$-representations. Projecting (8.10) to the
$\mathbb {G}_r(\mathbb {F}_q)$-representations. Projecting (8.10) to the ![]() $\theta ^{\otimes \ell }$-isotypic component and then using (8.5) to relate the Frobenius twist of the
$\theta ^{\otimes \ell }$-isotypic component and then using (8.5) to relate the Frobenius twist of the ![]() $\theta$-isotypic component with the
$\theta$-isotypic component with the ![]() $\theta ^{\otimes \ell }$-isotypic component, the proof is concluded.
$\theta ^{\otimes \ell }$-isotypic component, the proof is concluded.
8.3 Tate cohomology of compact inductions
We study the relationship between compact induction and Tate cohomology. In this section, we let ![]() $G'/F$ be a reductive group and
$G'/F$ be a reductive group and ![]() $\mathsf {G}' = G'(F)$ with an action of
$\mathsf {G}' = G'(F)$ with an action of ![]() $\mathbb {Z}/\ell \mathbb {Z} \cong \langle \sigma \rangle$,
$\mathbb {Z}/\ell \mathbb {Z} \cong \langle \sigma \rangle$, ![]() $\mathsf {H}' \subset \mathsf {G}'$ a
$\mathsf {H}' \subset \mathsf {G}'$ a ![]() $\sigma$-invariant open subgroup,
$\sigma$-invariant open subgroup, ![]() $\mathsf {G} = (\mathsf {G}')^{\sigma }$ and
$\mathsf {G} = (\mathsf {G}')^{\sigma }$ and ![]() $\mathsf {H} = (\mathsf {H}')^{\sigma }$.
$\mathsf {H} = (\mathsf {H}')^{\sigma }$.
Proposition 8.12 Let ![]() $\pi$ be a finite-dimensional representation of
$\pi$ be a finite-dimensional representation of ![]() $\mathsf {H}$. If
$\mathsf {H}$. If ![]() $\mathsf {G}/\mathsf {H} \xrightarrow {\sim } (\mathsf {G}'/\mathsf {H}')^{\sigma }$, then
$\mathsf {G}/\mathsf {H} \xrightarrow {\sim } (\mathsf {G}'/\mathsf {H}')^{\sigma }$, then
as ![]() $\mathsf {G}'$-representations.
$\mathsf {G}'$-representations.
Proof. A special case appears in [Reference RonchettiRon16, Proposition 14], which already contains the main ideas of the proof. We use Bernstein and Zelevinsky's perspective of ![]() $l$-sheaves on
$l$-sheaves on ![]() $l$-spaces. There is an equivalence of categories between
$l$-spaces. There is an equivalence of categories between ![]() $\mathsf {G}'$-equivariant sheaves on
$\mathsf {G}'$-equivariant sheaves on ![]() $\mathsf {G}'/\mathsf {H}'$ and representations of
$\mathsf {G}'/\mathsf {H}'$ and representations of ![]() $\mathsf {H}'$, which we denote
$\mathsf {H}'$, which we denote ![]() ${\mathcal {F}}_{\pi } \leftrightarrow \pi$. Furthermore, the Tate cohomology of
${\mathcal {F}}_{\pi } \leftrightarrow \pi$. Furthermore, the Tate cohomology of ![]() ${\mathcal {F}}_{\pi }$ as a sheaf transports to the Tate cohomology of
${\mathcal {F}}_{\pi }$ as a sheaf transports to the Tate cohomology of ![]() $\pi$ as a representation.
$\pi$ as a representation.
Under this equivalence and the analogous equivalence between ![]() $\mathsf {G}'$-equivariant sheaves on a point and
$\mathsf {G}'$-equivariant sheaves on a point and ![]() $\mathsf {G}'$-representations, the
$\mathsf {G}'$-representations, the ![]() $\mathsf {G}'$-representation
$\mathsf {G}'$-representation ![]() $\operatorname {c-Ind}_{\mathsf {H}'}^{\mathsf {G}'}(\pi )$ corresponds to the
$\operatorname {c-Ind}_{\mathsf {H}'}^{\mathsf {G}'}(\pi )$ corresponds to the ![]() $\mathsf {G}'$-equivariant sheaf
$\mathsf {G}'$-equivariant sheaf ![]() $\operatorname {pr}_! {\mathcal {F}}_{\pi }$ on
$\operatorname {pr}_! {\mathcal {F}}_{\pi }$ on ![]() $\operatorname {pt}$, where
$\operatorname {pt}$, where ![]() $\operatorname {pr} \colon \mathsf {G}' / \mathsf {H}' \rightarrow \operatorname {pt}$, under the functor of taking global sections for
$\operatorname {pr} \colon \mathsf {G}' / \mathsf {H}' \rightarrow \operatorname {pt}$, under the functor of taking global sections for ![]() $\mathsf {G}'$-equivariant sheaves on
$\mathsf {G}'$-equivariant sheaves on ![]() $\operatorname {pt}$. By [Reference Treumann and VenkateshTV16, § 3.3], the restriction map on sections induces
$\operatorname {pt}$. By [Reference Treumann and VenkateshTV16, § 3.3], the restriction map on sections induces
which completes the proof.
Next we work out some situations where the hypothesis of Proposition 8.12 is satisfied. We have the long exact sequence
so ![]() $\mathsf {G}/\mathsf {H} \xrightarrow {\sim } (\mathsf {G}'/\mathsf {H}')^{\sigma }$ if
$\mathsf {G}/\mathsf {H} \xrightarrow {\sim } (\mathsf {G}'/\mathsf {H}')^{\sigma }$ if ![]() $H^1(\langle \sigma \rangle, \mathsf {H}') = 0$.
$H^1(\langle \sigma \rangle, \mathsf {H}') = 0$.
Lemma 8.13 Let ![]() $F_{\ell }/F$ be the unramified
$F_{\ell }/F$ be the unramified ![]() $\mathbb {Z}/\ell \mathbb {Z}$-extension of local fields of characteristic
$\mathbb {Z}/\ell \mathbb {Z}$-extension of local fields of characteristic ![]() $p \neq \ell$. Let
$p \neq \ell$. Let ![]() $H$ be a connected algebraic group over
$H$ be a connected algebraic group over ![]() ${\mathcal {O}}_F$ and
${\mathcal {O}}_F$ and ![]() $\mathsf {H}' = H({\mathcal {O}}_{F_{\ell }})$, with the action of
$\mathsf {H}' = H({\mathcal {O}}_{F_{\ell }})$, with the action of ![]() $\operatorname {Gal}(F_{\ell }/F) \cong \langle \sigma \rangle$ by Galois conjugation on points. Then
$\operatorname {Gal}(F_{\ell }/F) \cong \langle \sigma \rangle$ by Galois conjugation on points. Then ![]() $H^1(\sigma, \mathsf {H}')= 0$.
$H^1(\sigma, \mathsf {H}')= 0$.
Proof. Let ![]() $\mathsf {H}^+$ be the kernel of the reduction map
$\mathsf {H}^+$ be the kernel of the reduction map ![]() $\mathsf {H}' = H({\mathcal {O}}_{F_{\ell }}) \rightarrow H(\mathbb {F}_{q^\ell })$. From the long exact sequence of cohomology, we have the exact sequence
$\mathsf {H}' = H({\mathcal {O}}_{F_{\ell }}) \rightarrow H(\mathbb {F}_{q^\ell })$. From the long exact sequence of cohomology, we have the exact sequence
Since ![]() $\mathsf {H}'_+$ is pro-
$\mathsf {H}'_+$ is pro-![]() $p$, we have
$p$, we have ![]() $H^1(\sigma, \mathsf {H}'_+) = 0$. By Lang's theorem,
$H^1(\sigma, \mathsf {H}'_+) = 0$. By Lang's theorem, ![]() $H^1(\sigma, H(\mathbb {F}_{q^\ell })) = 0$. Therefore,
$H^1(\sigma, H(\mathbb {F}_{q^\ell })) = 0$. Therefore, ![]() $H^1(\sigma, \mathsf {H}') = 0$.
$H^1(\sigma, \mathsf {H}') = 0$.
We shall be particularly interested in the case where ![]() $\mathsf {G}' = G(F_{\ell })$ and
$\mathsf {G}' = G(F_{\ell })$ and ![]() $\mathsf {H'} = Z(\mathsf {G}') G(F_{\ell })_{x,0}$ for
$\mathsf {H'} = Z(\mathsf {G}') G(F_{\ell })_{x,0}$ for ![]() $x \in {\mathcal {B}}(G/F_{\ell })$ fixed by
$x \in {\mathcal {B}}(G/F_{\ell })$ fixed by ![]() $\operatorname {Gal}(F_{\ell }/F)$, which guarantees that
$\operatorname {Gal}(F_{\ell }/F)$, which guarantees that ![]() $\mathsf {H'}$ is stable under
$\mathsf {H'}$ is stable under ![]() $\operatorname {Gal}(F_{\ell }/F)$. By unramified descent in Bruhat–Tits theory,
$\operatorname {Gal}(F_{\ell }/F)$. By unramified descent in Bruhat–Tits theory, ![]() $G(F_{\ell })_{x,0}^{\operatorname {Gal}(F_{\ell }/F)} = G(F)_{x,0}$, so we have
$G(F_{\ell })_{x,0}^{\operatorname {Gal}(F_{\ell }/F)} = G(F)_{x,0}$, so we have ![]() $\mathsf {G} := (\mathsf {G}')^{\operatorname {Gal}(F_{\ell }/F)} = G(F)$ and
$\mathsf {G} := (\mathsf {G}')^{\operatorname {Gal}(F_{\ell }/F)} = G(F)$ and ![]() $\mathsf {H} := (\mathsf {H}')^{\operatorname {Gal}(F_{\ell }/F)} = Z(\mathsf {G}) G(F)_{x,0}$.
$\mathsf {H} := (\mathsf {H}')^{\operatorname {Gal}(F_{\ell }/F)} = Z(\mathsf {G}) G(F)_{x,0}$.
Let ![]() $Z \subset G$ be the maximal central torus. Then
$Z \subset G$ be the maximal central torus. Then ![]() $Z_{F_{\ell }}$ is the maximal central torus of
$Z_{F_{\ell }}$ is the maximal central torus of ![]() $G_{F_{\ell }}$.
$G_{F_{\ell }}$.
Lemma 8.14 Assume that:
(i) the action of
 $\operatorname {Gal}(F_{\ell }/F)$ on the cocharacter group
$\operatorname {Gal}(F_{\ell }/F)$ on the cocharacter group  $X^*(Z_{F_{\ell }})$ is trivial;
$X^*(Z_{F_{\ell }})$ is trivial;(ii) the component group
 $Z(\mathsf {G}')/Z$ has order coprime to
$Z(\mathsf {G}')/Z$ has order coprime to  $\ell$.
$\ell$.
Let ![]() $H' = Z(\mathsf {G}')G(F_\ell )_{x,0}$. Then
$H' = Z(\mathsf {G}')G(F_\ell )_{x,0}$. Then ![]() $H^1(\sigma, \mathsf {H}') = 0$.
$H^1(\sigma, \mathsf {H}') = 0$.
Example Assumption (i) is satisfied, for example, if ![]() $G$ is split reductive, or whenever
$G$ is split reductive, or whenever ![]() $G$ is (not necessarily split and) semisimple. For any given
$G$ is (not necessarily split and) semisimple. For any given ![]() $G$, assumption (ii) is satisfied for all large enough
$G$, assumption (ii) is satisfied for all large enough ![]() $\ell$.
$\ell$.
Proof. Since ![]() $G$ is assumed to be split over an unramified extension of
$G$ is assumed to be split over an unramified extension of ![]() $F$,
$F$, ![]() $Z$ is an unramified torus, hence has a canonical integral model
$Z$ is an unramified torus, hence has a canonical integral model ![]() ${\mathcal {Z}}/{\mathcal {O}}_F$ (the ‘connected Néron model’), which has the property that
${\mathcal {Z}}/{\mathcal {O}}_F$ (the ‘connected Néron model’), which has the property that ![]() ${\mathcal {Z}}({\mathcal {O}}_F)$ is the maximal bounded subgroup of
${\mathcal {Z}}({\mathcal {O}}_F)$ is the maximal bounded subgroup of ![]() $Z(F)$. We have a split short exact sequence
$Z(F)$. We have a split short exact sequence
where ![]() $Z(F_\ell ) / {\mathcal {Z}}({\mathcal {O}}_{F_{\ell }}) \cong X_*(Z_{F_{\ell }})$ is torsion-free, and
$Z(F_\ell ) / {\mathcal {Z}}({\mathcal {O}}_{F_{\ell }}) \cong X_*(Z_{F_{\ell }})$ is torsion-free, and ![]() ${\mathcal {Z}}({\mathcal {O}}_{F_{\ell }}) = Z(F_{\ell }) \cap G(F_{\ell })_{x,0} \subset G(F_{\ell })_{x,0}$. Therefore,
${\mathcal {Z}}({\mathcal {O}}_{F_{\ell }}) = Z(F_{\ell }) \cap G(F_{\ell })_{x,0} \subset G(F_{\ell })_{x,0}$. Therefore, ![]() $Z(F_{\ell }) G(F_{\ell })_{x,0} \cong X_*(Z_{F_{\ell }}) \times G(F_{\ell })_{x,0}$ so
$Z(F_{\ell }) G(F_{\ell })_{x,0} \cong X_*(Z_{F_{\ell }}) \times G(F_{\ell })_{x,0}$ so
Now, ![]() $H^1(\sigma, X_*(Z_{F_{\ell }})) = 0$ because the assumed condition (i) implies
$H^1(\sigma, X_*(Z_{F_{\ell }})) = 0$ because the assumed condition (i) implies ![]() $H^1(\sigma, X_*(Z_{F_{\ell }})) \cong \operatorname {Hom}(\langle \sigma \rangle, X_*(Z_{F_{\ell }})) = 0$. Since
$H^1(\sigma, X_*(Z_{F_{\ell }})) \cong \operatorname {Hom}(\langle \sigma \rangle, X_*(Z_{F_{\ell }})) = 0$. Since ![]() $G(F_{\ell })_{x,0}$ is the group of
$G(F_{\ell })_{x,0}$ is the group of ![]() ${\mathcal {O}}_{F_{\ell }}$-points of a connected Bruhat–Tits group scheme, the group
${\mathcal {O}}_{F_{\ell }}$-points of a connected Bruhat–Tits group scheme, the group ![]() $H^1(\sigma, G(F_{\ell })_{x,0})$ vanishes by Lemma 8.13. Therefore,
$H^1(\sigma, G(F_{\ell })_{x,0})$ vanishes by Lemma 8.13. Therefore, ![]() $H^1(\sigma, Z(F_{\ell }) G(F_{\ell })_{x,0}) = 0$.
$H^1(\sigma, Z(F_{\ell }) G(F_{\ell })_{x,0}) = 0$.
Finally, assumption (ii) implies that the index of ![]() $Z(F_{\ell }) G(F_{\ell })_{x,0}$ is a normal subgroup of
$Z(F_{\ell }) G(F_{\ell })_{x,0}$ is a normal subgroup of ![]() $Z(\mathsf {G}')G(F_{\ell })_{x,0}$ with finite index coprime to
$Z(\mathsf {G}')G(F_{\ell })_{x,0}$ with finite index coprime to ![]() $\ell$, so the long exact sequence implies that
$\ell$, so the long exact sequence implies that ![]() $H^1(\sigma, Z(\mathsf {G}')G(F_{\ell })_{x,0}) = 0$.
$H^1(\sigma, Z(\mathsf {G}')G(F_{\ell })_{x,0}) = 0$.
8.4 Toral supercuspidal representations
We will prove base change results for a class of supercuspidal representations studied by Chan and Oi in [Reference Chan and OiCO23], which should correspond (in the language of [Reference Chan and OiCO23]) to 0-toral Howe-unramified supercuspidal ![]() $L$-parameters.
$L$-parameters.
8.4.1 Assumptions
We impose the same assumptions as in [Reference Chan and OiCO23, § 7]. In particular, ![]() $G$ is a reductive group over
$G$ is a reductive group over ![]() $F$,
$F$, ![]() $p$ is odd and not bad for
$p$ is odd and not bad for ![]() $G$,
$G$, ![]() $p \nmid \pi _1(G_{\mathrm {der}})$, and
$p \nmid \pi _1(G_{\mathrm {der}})$, and ![]() $p \nmid \pi _1(\widehat {G}_{\mathrm {der}})$. The maximal torus
$p \nmid \pi _1(\widehat {G}_{\mathrm {der}})$. The maximal torus ![]() $T \subset G$ is unramified elliptic, and
$T \subset G$ is unramified elliptic, and ![]() $\widetilde {\theta } \colon T(F) \rightarrow \overline {\mathbb {Z}}_{\ell }^{\times }$ is
$\widetilde {\theta } \colon T(F) \rightarrow \overline {\mathbb {Z}}_{\ell }^{\times }$ is ![]() $0$-toral and of depth
$0$-toral and of depth ![]() $r >0$, i.e. trivial on
$r >0$, i.e. trivial on ![]() $T_{x,r+}$ for some
$T_{x,r+}$ for some ![]() $x \in {\mathcal {B}}(G/F)$. We write
$x \in {\mathcal {B}}(G/F)$. We write ![]() $\theta \colon T \rightarrow k^{\times }$ for the reduction of
$\theta \colon T \rightarrow k^{\times }$ for the reduction of ![]() $\widetilde {\theta }$ modulo
$\widetilde {\theta }$ modulo ![]() $\ell$ (where we recall that
$\ell$ (where we recall that ![]() $k$ is an algebraic closure of
$k$ is an algebraic closure of ![]() $\mathbb {F}_\ell$). We assume that
$\mathbb {F}_\ell$). We assume that ![]() $R_{\mathbb {T}_r, \mathbb {U}_r}^{\mathbb {G}_r}(\widetilde {\theta })$ is non-zero, which is automatic under a mild regularity hypothesis (see the proof of Lemma 8.4(ii)).
$R_{\mathbb {T}_r, \mathbb {U}_r}^{\mathbb {G}_r}(\widetilde {\theta })$ is non-zero, which is automatic under a mild regularity hypothesis (see the proof of Lemma 8.4(ii)).
8.4.2 Work of Chan and Oi
The assumptions imply that ![]() $R_{\mathbb {T}_r, \mathbb {U}_r}^{\mathbb {G}_r}(\widetilde {\theta }) \otimes _{\overline {\mathbb {Z}}_{\ell }} \overline {\mathbb {Q}}_{\ell }$ is irreducible and independent of the choice of
$R_{\mathbb {T}_r, \mathbb {U}_r}^{\mathbb {G}_r}(\widetilde {\theta }) \otimes _{\overline {\mathbb {Z}}_{\ell }} \overline {\mathbb {Q}}_{\ell }$ is irreducible and independent of the choice of ![]() $\mathbb {U}_r$, hence we simply abbreviate it as
$\mathbb {U}_r$, hence we simply abbreviate it as ![]() $R_{\mathbb {T}_r}^{\mathbb {G}_r}(\widetilde {\theta })_{\overline {\mathbb {Q}}_{\ell }}$. Furthermore, by [Reference Chan and OiCO23, Theorem 7.2] the
$R_{\mathbb {T}_r}^{\mathbb {G}_r}(\widetilde {\theta })_{\overline {\mathbb {Q}}_{\ell }}$. Furthermore, by [Reference Chan and OiCO23, Theorem 7.2] the ![]() $\overline {\mathbb {Q}}_{\ell }$-representation
$\overline {\mathbb {Q}}_{\ell }$-representation ![]() $\operatorname {c-Ind}_{T(F)G(F)_{x,0}}^G( | R_{\mathbb {T}_r}^{\mathbb {G}_r}(\widetilde {\theta })_{\overline {\mathbb {Q}}_{\ell }}|)$ is irreducible supercuspidal.
$\operatorname {c-Ind}_{T(F)G(F)_{x,0}}^G( | R_{\mathbb {T}_r}^{\mathbb {G}_r}(\widetilde {\theta })_{\overline {\mathbb {Q}}_{\ell }}|)$ is irreducible supercuspidal.
Given ![]() $\widetilde {\theta }$, there is defined in [Reference Chan and OiCO23, Definition 4.8] a certain sign character
$\widetilde {\theta }$, there is defined in [Reference Chan and OiCO23, Definition 4.8] a certain sign character ![]() $\epsilon ^{\mathrm {ram}}[\widetilde {\theta }] \colon T(F) \rightarrow \overline {\mathbb {Q}}_{\ell }^{\times }$. We define
$\epsilon ^{\mathrm {ram}}[\widetilde {\theta }] \colon T(F) \rightarrow \overline {\mathbb {Q}}_{\ell }^{\times }$. We define
The twisting by ![]() $\epsilon ^{\mathrm {ram}}[\widetilde {\theta }]$ is for consistency with Kaletha's indexing of regular supercuspidal representations [Reference KalethaKal19];
$\epsilon ^{\mathrm {ram}}[\widetilde {\theta }]$ is for consistency with Kaletha's indexing of regular supercuspidal representations [Reference KalethaKal19]; ![]() $\pi _{T, \widetilde {\theta } \cdot \epsilon ^{\mathrm {ram}}[\widetilde {\theta }] }$ is a regular supercuspidal representation by [Reference Chan and OiCO23, Theorem 7.2]. In particular, it is irreducible.
$\pi _{T, \widetilde {\theta } \cdot \epsilon ^{\mathrm {ram}}[\widetilde {\theta }] }$ is a regular supercuspidal representation by [Reference Chan and OiCO23, Theorem 7.2]. In particular, it is irreducible.
Since ![]() $\epsilon ^{\mathrm {ram}}[\widetilde {\theta }]$ takes values in
$\epsilon ^{\mathrm {ram}}[\widetilde {\theta }]$ takes values in ![]() $\{\pm 1\}$, we may regard it also as a character valued in
$\{\pm 1\}$, we may regard it also as a character valued in ![]() $\overline {\mathbb {F}}_{\ell }^{\times }$ by reduction modulo
$\overline {\mathbb {F}}_{\ell }^{\times }$ by reduction modulo ![]() $\ell$. We may define
$\ell$. We may define
A priori this is only a class in ![]() $K_0(G(F); \overline {\mathbb {F}}_{\ell })$, but there are two circumstances in which we can lift it to an honest representation, which will be denoted
$K_0(G(F); \overline {\mathbb {F}}_{\ell })$, but there are two circumstances in which we can lift it to an honest representation, which will be denoted ![]() $|\pi _{T, \theta \cdot \epsilon ^{\mathrm {ram}}[\theta ]}|$:
$|\pi _{T, \theta \cdot \epsilon ^{\mathrm {ram}}[\theta ]}|$:
• If
 $\ell$ is banal, in which case we may lift
$\ell$ is banal, in which case we may lift  $\pm R_{\mathbb {T}_r, \mathbb {U}_r}(\theta )$ to a representation
$\pm R_{\mathbb {T}_r, \mathbb {U}_r}(\theta )$ to a representation  $|R_{\mathbb {T}_r, \mathbb {U}_r}(\theta )|$.
$|R_{\mathbb {T}_r, \mathbb {U}_r}(\theta )|$.• If
 $H_c^{*}(Y_{\mathbb {T}_r, \mathbb {U}_r}; E)_{\widetilde {\theta }}$ concentrates in a single degree (where we recall from § 2.3 that
$H_c^{*}(Y_{\mathbb {T}_r, \mathbb {U}_r}; E)_{\widetilde {\theta }}$ concentrates in a single degree (where we recall from § 2.3 that  $E$ denotes some sufficiently large extension of
$E$ denotes some sufficiently large extension of  $\mathbb {Q}_\ell$, containing the values of
$\mathbb {Q}_\ell$, containing the values of  $\widetilde {\theta }$), in which case we define
In this case
$\widetilde {\theta }$), in which case we define
In this case \[ |\pi_{T, \theta \cdot \epsilon^{\mathrm{ram}}[\theta]}| := \operatorname{c-Ind}_{T(F)G(F)_{x,0}}^{G(F)} ( H_c^{*}(Y_{\mathbb{T}_r, \mathbb{U}_r}; {\mathcal{O}})_{\mathrm{tf}, \widetilde{\theta}} \otimes_{{\mathcal{O}}} k ). \]
\[ |\pi_{T, \theta \cdot \epsilon^{\mathrm{ram}}[\theta]}| := \operatorname{c-Ind}_{T(F)G(F)_{x,0}}^{G(F)} ( H_c^{*}(Y_{\mathbb{T}_r, \mathbb{U}_r}; {\mathcal{O}})_{\mathrm{tf}, \widetilde{\theta}} \otimes_{{\mathcal{O}}} k ). \]
 $|\pi _{T, \theta \cdot \epsilon ^{\mathrm {ram}}[\theta ]}|$ is the mod
$|\pi _{T, \theta \cdot \epsilon ^{\mathrm {ram}}[\theta ]}|$ is the mod  $\ell$ reduction of a
$\ell$ reduction of a  $\overline {\mathbb {Z}}_{\ell }$-lattice in
$\overline {\mathbb {Z}}_{\ell }$-lattice in  $\pi _{T, \widetilde {\theta } \cdot \epsilon ^{\mathrm {ram}}[\widetilde {\theta }] }$, namely the one induced by the lattice
$\pi _{T, \widetilde {\theta } \cdot \epsilon ^{\mathrm {ram}}[\widetilde {\theta }] }$, namely the one induced by the lattice  $H_c^{*}(Y_{\mathbb {T}_r, \mathbb {U}_r}; {\mathcal {O}})_{\mathrm {tf}, \widetilde {\theta }} \subset |R_{\mathbb {T}_r, \mathbb {U}_r}(\widetilde {\theta })|$. Hence, if
$H_c^{*}(Y_{\mathbb {T}_r, \mathbb {U}_r}; {\mathcal {O}})_{\mathrm {tf}, \widetilde {\theta }} \subset |R_{\mathbb {T}_r, \mathbb {U}_r}(\widetilde {\theta })|$. Hence, if  $\ell$ is banal, then this definition coincides with the one in the previous bullet point, so that
$\ell$ is banal, then this definition coincides with the one in the previous bullet point, so that  $|\pi _{T, \theta \cdot \epsilon ^{\mathrm {ram}}[\theta ]}|$ is unambiguously defined. Furthermore, if (8.3) is satisfied, then by Lemma 8.7 we have
$|\pi _{T, \theta \cdot \epsilon ^{\mathrm {ram}}[\theta ]}|$ is unambiguously defined. Furthermore, if (8.3) is satisfied, then by Lemma 8.7 we have
 \[ |\pi_{T, \theta \cdot \epsilon^{\mathrm{ram}}[\theta]}| \cong \operatorname{c-Ind}_{T(F)G(F)_{x,0}}^{G(F)} ( H_c^{*}(Y_{\mathbb{T}_r, \mathbb{U}_r}; k)_{\theta}). \]
\[ |\pi_{T, \theta \cdot \epsilon^{\mathrm{ram}}[\theta]}| \cong \operatorname{c-Ind}_{T(F)G(F)_{x,0}}^{G(F)} ( H_c^{*}(Y_{\mathbb{T}_r, \mathbb{U}_r}; k)_{\theta}). \]
Proposition 8.15 If ![]() $\ell$ is banal for
$\ell$ is banal for ![]() $G$, then (under our running hypotheses) the representation
$G$, then (under our running hypotheses) the representation ![]() $\pi _{T, \theta \cdot \epsilon ^{\mathrm {ram}}[\theta ]}$ is irreducible and cuspidal.
$\pi _{T, \theta \cdot \epsilon ^{\mathrm {ram}}[\theta ]}$ is irreducible and cuspidal.
Proof. Indeed, [Reference Chan and OiCO23, Theorem 7.2] identifies ![]() $\pi _{T, \widetilde {\theta } \cdot \epsilon ^{\mathrm {ram}}[\widetilde {\theta }] }$ with the compact induction of Yu's representation, denoted
$\pi _{T, \widetilde {\theta } \cdot \epsilon ^{\mathrm {ram}}[\widetilde {\theta }] }$ with the compact induction of Yu's representation, denoted ![]() $^\circ \tau _d$ in [Reference Chan and OiCO23]. Since
$^\circ \tau _d$ in [Reference Chan and OiCO23]. Since ![]() $\ell$ is banal the mod
$\ell$ is banal the mod ![]() $\ell$ reduction of
$\ell$ reduction of ![]() $^\circ \tau _d$ is again irreducible and obtained from Yu's construction. Its compact induction is identified with
$^\circ \tau _d$ is again irreducible and obtained from Yu's construction. Its compact induction is identified with ![]() $\pi _{T, \theta \cdot \epsilon ^{\mathrm {ram}}[\theta ]}$. The result then follows from [Reference FintzenFin22, Theorem 6.1].
$\pi _{T, \theta \cdot \epsilon ^{\mathrm {ram}}[\theta ]}$. The result then follows from [Reference FintzenFin22, Theorem 6.1].
Remark 8.16 Marie-France Vignéras has indicated another proof of Proposition 8.15. Let
and let ![]() $[\tau ]$ denote the reduction mod
$[\tau ]$ denote the reduction mod ![]() $\ell$ of any
$\ell$ of any ![]() $\overline {\mathbb {Z}}_{\ell }$-lattice in
$\overline {\mathbb {Z}}_{\ell }$-lattice in ![]() $\tau$; this is independent of the choice because
$\tau$; this is independent of the choice because ![]() $\ell$ is banal. Write
$\ell$ is banal. Write ![]() $U = T(F)G(F)_{x,0}$. Lemma 3.2 of her article [Reference VignérasVig01] proves a simple criterion for irreducibility of the compact induction of
$U = T(F)G(F)_{x,0}$. Lemma 3.2 of her article [Reference VignérasVig01] proves a simple criterion for irreducibility of the compact induction of ![]() $[\tau ]$, which we adapt to our present notation:
$[\tau ]$, which we adapt to our present notation:
(a)
 $\operatorname {End}_{\overline {\mathbb {F}}_{\ell }[G]}(\operatorname {c-Ind}_{U}^G[\tau ]) = \overline {\mathbb {F}}_{\ell }$.
$\operatorname {End}_{\overline {\mathbb {F}}_{\ell }[G]}(\operatorname {c-Ind}_{U}^G[\tau ]) = \overline {\mathbb {F}}_{\ell }$.(b) Let
 $\pi$ be any irreducible
$\pi$ be any irreducible  $\overline {\mathbb {F}}_{\ell }$-representation of
$\overline {\mathbb {F}}_{\ell }$-representation of  $G$. If
$G$. If  $[\tau ]$ is contained in the restriction of
$[\tau ]$ is contained in the restriction of  $\pi$ to
$\pi$ to  $U$ then
$U$ then  $[\tau ]$ is also a quotient of
$[\tau ]$ is also a quotient of  $\pi |_U$.
$\pi |_U$.
Now (b) is automatic because ![]() $\ell$ is banal and therefore prime to the pro-order of
$\ell$ is banal and therefore prime to the pro-order of ![]() $U$. On the other hand, it follows from the supercuspidality of
$U$. On the other hand, it follows from the supercuspidality of ![]() $\operatorname {c-Ind}_U^G \tau$ that for any
$\operatorname {c-Ind}_U^G \tau$ that for any ![]() $g \in G \setminus U$ the restrictions of
$g \in G \setminus U$ the restrictions of ![]() $\tau$ and
$\tau$ and ![]() $g(\tau )$ to the intersection
$g(\tau )$ to the intersection ![]() $U \cap g Ug^{-1}$ are disjoint. Again, since
$U \cap g Ug^{-1}$ are disjoint. Again, since ![]() $\ell$ is banal, the same holds for the restrictions of
$\ell$ is banal, the same holds for the restrictions of ![]() $[\tau ]$ and
$[\tau ]$ and ![]() $g([\tau ])$. Point (a) then follows, and this implies irreducibility. Cuspidality is then a consequence of [Reference VignérasVig96, Theorem II.2.7], because the matrix coefficients of the compactly induced representation are compact modulo center.
$g([\tau ])$. Point (a) then follows, and this implies irreducibility. Cuspidality is then a consequence of [Reference VignérasVig96, Theorem II.2.7], because the matrix coefficients of the compactly induced representation are compact modulo center.
8.4.3 Base change
Let ![]() $G$ be a reductive group over
$G$ be a reductive group over ![]() $F$ and
$F$ and ![]() $F'/F$ a
$F'/F$ a ![]() $\mathbb {Z}/\ell \mathbb {Z}$-extension. Let
$\mathbb {Z}/\ell \mathbb {Z}$-extension. Let ![]() $\pi '$ be an irreducible (admissible) representation of
$\pi '$ be an irreducible (admissible) representation of ![]() $G(F')$ over
$G(F')$ over ![]() $\overline {\mathbb {F}}_{\ell }$. Choose a generator
$\overline {\mathbb {F}}_{\ell }$. Choose a generator ![]() $\sigma$ of
$\sigma$ of ![]() $\operatorname {Gal}(F'/F) \cong \mathbb {Z}/\ell \mathbb {Z}$. Then
$\operatorname {Gal}(F'/F) \cong \mathbb {Z}/\ell \mathbb {Z}$. Then ![]() $\sigma$ acts on
$\sigma$ acts on ![]() $G(F')$ through its Galois action on
$G(F')$ through its Galois action on ![]() $E$. We say that
$E$. We say that ![]() $\pi '$ is
$\pi '$ is ![]() $\sigma$-fixed if
$\sigma$-fixed if ![]() $\pi ' \cong \pi ' \circ \sigma$ as
$\pi ' \cong \pi ' \circ \sigma$ as ![]() $G(F')$-representations.
$G(F')$-representations.
Lemma 8.17 [Reference Treumann and VenkateshTV16, Proposition 6.1]
If ![]() $\pi '$ is
$\pi '$ is ![]() $\sigma$-fixed, then the action of
$\sigma$-fixed, then the action of ![]() $G(F')$ extends uniquely to a
$G(F')$ extends uniquely to a ![]() $G(F') \rtimes \langle \sigma \rangle$-action.
$G(F') \rtimes \langle \sigma \rangle$-action.
The Tate cohomology groups of ![]() $\pi '$, with respect to the
$\pi '$, with respect to the ![]() $\sigma$-action, are
$\sigma$-action, are
The ![]() $G(F')$-action on
$G(F')$-action on ![]() $\pi '$ induces an action of
$\pi '$ induces an action of ![]() $G(F)$ on
$G(F)$ on ![]() $\mathrm {T}^i(\pi ')$.
$\mathrm {T}^i(\pi ')$.
Let ![]() $\pi$ be an irreducible admissible representation of
$\pi$ be an irreducible admissible representation of ![]() $G(F)$ over
$G(F)$ over ![]() $\overline {\mathbb {F}}_{\ell }$, and
$\overline {\mathbb {F}}_{\ell }$, and ![]() $\pi '$ be an irreducible admissible representation of
$\pi '$ be an irreducible admissible representation of ![]() $G(F')$ over
$G(F')$ over ![]() $\overline {\mathbb {F}}_{\ell }$. Recall that in Definition 7.1 we defined what it means for
$\overline {\mathbb {F}}_{\ell }$. Recall that in Definition 7.1 we defined what it means for ![]() $\pi '$ to be a base change of
$\pi '$ to be a base change of ![]() $\pi$. In this situation we say that
$\pi$. In this situation we say that ![]() $\pi$ is a base change descent of
$\pi$ is a base change descent of ![]() $\pi '$. Addressing [Reference Treumann and VenkateshTV16, Conjecture 6.5], it was proved in [Reference FengFen24, Theorem 1.2] that if
$\pi '$. Addressing [Reference Treumann and VenkateshTV16, Conjecture 6.5], it was proved in [Reference FengFen24, Theorem 1.2] that if ![]() $F$ has characteristic
$F$ has characteristic ![]() $p\neq \ell$, and
$p\neq \ell$, and ![]() $\ell$ is odd and good for
$\ell$ is odd and good for ![]() $\widehat {G}$, then any irreducible
$\widehat {G}$, then any irreducible ![]() $G(F)$-subquotient
$G(F)$-subquotient ![]() $\pi$ of
$\pi$ of ![]() $\mathrm {T}^i(\pi ')$ base-changes to
$\mathrm {T}^i(\pi ')$ base-changes to ![]() $(\pi ')^{(\ell )}$, the Frobenius twist of
$(\pi ')^{(\ell )}$, the Frobenius twist of ![]() $\pi '$. The theorem below computes Tate cohomology of mod
$\pi '$. The theorem below computes Tate cohomology of mod ![]() $\ell$ toral supercuspidal representations for
$\ell$ toral supercuspidal representations for ![]() $F' = F_{\ell }$ the unramified extension of order
$F' = F_{\ell }$ the unramified extension of order ![]() $\ell$.
$\ell$.
Theorem 8.18 Let ![]() $G,T, \theta$ be as in § 8.4.1. Let
$G,T, \theta$ be as in § 8.4.1. Let ![]() $G', T', \theta '$ be as in § 8.2.4. Assume that
$G', T', \theta '$ be as in § 8.2.4. Assume that ![]() $T(F_{\ell })$ is elliptic.
$T(F_{\ell })$ is elliptic.
(i) Assume that
 $\ell \nmid \# \mathbb {T}_0(\mathbb {F}_q)$ and
$\ell \nmid \# \mathbb {T}_0(\mathbb {F}_q)$ and  $G$ satisfies the assumptions of Lemma 8.14. If
$G$ satisfies the assumptions of Lemma 8.14. If  $H_c^*(Y_{\mathbb {T}_r, \mathbb {U}_r}, \overline {\mathbb {F}}_{\ell })_{\theta } \neq 0$, then there exist
$H_c^*(Y_{\mathbb {T}_r, \mathbb {U}_r}, \overline {\mathbb {F}}_{\ell })_{\theta } \neq 0$, then there exist  $i \in \{0,1\}$,
$i \in \{0,1\}$,  $i'$ such that
$i'$ such that
 \[ \mathrm{T}^i \Big( \operatorname{c-Ind}_{T(F_{\ell})G(F_{\ell})_{x,0}}^{G(F_{\ell})} H_c^{i'}(Y_{\mathbb{T}_r' ,\mathbb{U}_r'}; \overline{\mathbb{F}}_{\ell} )_{\theta'} \Big)\neq 0. \]
\[ \mathrm{T}^i \Big( \operatorname{c-Ind}_{T(F_{\ell})G(F_{\ell})_{x,0}}^{G(F_{\ell})} H_c^{i'}(Y_{\mathbb{T}_r' ,\mathbb{U}_r'}; \overline{\mathbb{F}}_{\ell} )_{\theta'} \Big)\neq 0. \]
(ii) In addition to the assumptions from (i), suppose further that
 $\theta$ and
$\theta$ and  $\theta '$ both satisfy (8.3). Then we have an isomorphism of
$\theta '$ both satisfy (8.3). Then we have an isomorphism of  $G(F)$-representations for each
$G(F)$-representations for each  $i \in \mathbb {Z}/2\mathbb {Z}$,
In particular, the left-hand side is independent of
$i \in \mathbb {Z}/2\mathbb {Z}$,
In particular, the left-hand side is independent of \[ \mathrm{T}^i(\pi_{T', \theta' \cdot \epsilon^{\mathrm{ram}}[\theta' ]}) \cong \pi_{T, \theta \cdot \epsilon^{\mathrm{ram}}[\theta]}^{(\ell)}. \]
\[ \mathrm{T}^i(\pi_{T', \theta' \cdot \epsilon^{\mathrm{ram}}[\theta' ]}) \cong \pi_{T, \theta \cdot \epsilon^{\mathrm{ram}}[\theta]}^{(\ell)}. \]
 $i$.
$i$.
Proof. (i) Since ![]() $T(F_{\ell })$ is elliptic, we have
$T(F_{\ell })$ is elliptic, we have ![]() $T(F_{\ell })G(F_{\ell })_{x,0} = Z(G(F_{\ell })) G(F_{\ell })_{x,0}$. By Lemma 8.14, we may then apply Proposition 8.12 to deduce that
$T(F_{\ell })G(F_{\ell })_{x,0} = Z(G(F_{\ell })) G(F_{\ell })_{x,0}$. By Lemma 8.14, we may then apply Proposition 8.12 to deduce that
By Theorem 8.8, there exist ![]() $i$ and
$i$ and ![]() $i'$ for which
$i'$ for which ![]() $\mathrm {T}^i (H_c^{i'}(Y_{\mathbb {T}_r' ,\mathbb {U}_r'}; \overline {\mathbb {F}}_{\ell } )_{\theta '} \neq 0$.
$\mathrm {T}^i (H_c^{i'}(Y_{\mathbb {T}_r' ,\mathbb {U}_r'}; \overline {\mathbb {F}}_{\ell } )_{\theta '} \neq 0$.
(ii) Let ![]() $j$ and
$j$ and ![]() $j'$ be the non-vanishing degrees of
$j'$ be the non-vanishing degrees of ![]() $H_c^{*}(Y_{\mathbb {T}_r, \mathbb {U}_r}; \overline {\mathbb {F}}_{\ell })_{\theta }$ and
$H_c^{*}(Y_{\mathbb {T}_r, \mathbb {U}_r}; \overline {\mathbb {F}}_{\ell })_{\theta }$ and ![]() $H_c^{*}(Y_{\mathbb {T}_r', \mathbb {U}_r'}; \overline {\mathbb {F}}_{\ell })_{\theta '}$, respectively. By Lemma 8.7, the assumptions imply that:
$H_c^{*}(Y_{\mathbb {T}_r', \mathbb {U}_r'}; \overline {\mathbb {F}}_{\ell })_{\theta '}$, respectively. By Lemma 8.7, the assumptions imply that:
•
 $H_c^{*}(Y_{\mathbb {T}_r', \mathbb {U}_r'}; \overline {\mathbb {Z}}_{\ell })_{\mathrm {tf}, \widetilde {\theta }'} \otimes _{\overline {\mathbb {Z}}_{\ell }} \overline {\mathbb {F}}_{\ell } \cong H_c^{*}(Y_{\mathbb {T}_r', \mathbb {U}_r'}; \overline {\mathbb {F}}_{\ell })_{\theta '}$ as representations of
$H_c^{*}(Y_{\mathbb {T}_r', \mathbb {U}_r'}; \overline {\mathbb {Z}}_{\ell })_{\mathrm {tf}, \widetilde {\theta }'} \otimes _{\overline {\mathbb {Z}}_{\ell }} \overline {\mathbb {F}}_{\ell } \cong H_c^{*}(Y_{\mathbb {T}_r', \mathbb {U}_r'}; \overline {\mathbb {F}}_{\ell })_{\theta '}$ as representations of  $T(F_{\ell })G(F_{\ell })_{x,0}$, where
$T(F_{\ell })G(F_{\ell })_{x,0}$, where  $T(F_{\ell })$ acts through
$T(F_{\ell })$ acts through  $\theta '$ and
$\theta '$ and  $G(F_{\ell })_{x,0}$ acts through inflation from
$G(F_{\ell })_{x,0}$ acts through inflation from  $G(F_{\ell })_{x,0:r+}$;
$G(F_{\ell })_{x,0:r+}$;•
 $H_c^{*}(Y_{\mathbb {T}_r, \mathbb {U}_r}; \overline {\mathbb {Z}}_{\ell })_{\mathrm {tf}, \widetilde {\theta }} \otimes _{\overline {\mathbb {Z}}_{\ell }} \overline {\mathbb {F}}_{\ell } \cong H_c^{*}(Y_{\mathbb {T}_r, \mathbb {U}_r}; \overline {\mathbb {F}}_{\ell })_{\theta }$ as representations of
$H_c^{*}(Y_{\mathbb {T}_r, \mathbb {U}_r}; \overline {\mathbb {Z}}_{\ell })_{\mathrm {tf}, \widetilde {\theta }} \otimes _{\overline {\mathbb {Z}}_{\ell }} \overline {\mathbb {F}}_{\ell } \cong H_c^{*}(Y_{\mathbb {T}_r, \mathbb {U}_r}; \overline {\mathbb {F}}_{\ell })_{\theta }$ as representations of  $T(F)G(F)_{x,0}$, where
$T(F)G(F)_{x,0}$, where  $T(F)$ acts through
$T(F)$ acts through  $\theta$ and
$\theta$ and  $G(F)_{x,0}$ acts through inflation from
$G(F)_{x,0}$ acts through inflation from  $G(F)_{x,0:r+}$.
$G(F)_{x,0:r+}$.
By Lemma 8.14, we may apply Proposition 8.12 to deduce that
as ![]() $G(F)$-representations. Next, the assumptions that
$G(F)$-representations. Next, the assumptions that ![]() $\theta$ and
$\theta$ and ![]() $\theta '$ satisfy (8.3) allow us to apply Theorem 8.8(ii) to deduce that
$\theta '$ satisfy (8.3) allow us to apply Theorem 8.8(ii) to deduce that
as ![]() $T(F)G(F)_{x,0}$-representations. We then conclude by noting that Frobenius twist commutes with compact induction.
$T(F)G(F)_{x,0}$-representations. We then conclude by noting that Frobenius twist commutes with compact induction.
Remark 8.19 For a ![]() $\sigma$-fixed irreducible representation
$\sigma$-fixed irreducible representation ![]() $\pi '$ of
$\pi '$ of ![]() $G(F_{\ell })$, it is typically not obvious that
$G(F_{\ell })$, it is typically not obvious that ![]() $\mathrm {T}^i(\pi ') \neq 0$. (Thanks to [Reference FengFen24, Theorem 1.2], this would already imply that
$\mathrm {T}^i(\pi ') \neq 0$. (Thanks to [Reference FengFen24, Theorem 1.2], this would already imply that ![]() $\pi$ has a base change descent to
$\pi$ has a base change descent to ![]() $G(F)$.) We emphasize that our traction on the toral supercuspidal representations
$G(F)$.) We emphasize that our traction on the toral supercuspidal representations ![]() $\pi _{T, \theta \cdot \epsilon ^{\mathrm {ram}}[\theta ]}$ comes from the geometric description of these representations developed in [Reference Chan and IvanovCI21]. Another advantage of the geometric description, which was observed in [Reference Chan and OiCO23], is that it naturally incorporates the twisting character
$\pi _{T, \theta \cdot \epsilon ^{\mathrm {ram}}[\theta ]}$ comes from the geometric description of these representations developed in [Reference Chan and IvanovCI21]. Another advantage of the geometric description, which was observed in [Reference Chan and OiCO23], is that it naturally incorporates the twisting character ![]() $\epsilon ^{\mathrm {ram}}[\theta ]$.
$\epsilon ^{\mathrm {ram}}[\theta ]$.
Corollary 8.20 Let assumptions be as in Theorem 8.18(i),(ii) and suppose ![]() $\ell$ is odd and banal for
$\ell$ is odd and banal for ![]() $G$. Then
$G$. Then ![]() $\pi _{T, \theta \cdot \epsilon ^{\mathrm {ram}}[\theta ]}$ base-changes to
$\pi _{T, \theta \cdot \epsilon ^{\mathrm {ram}}[\theta ]}$ base-changes to ![]() $\pi _{T', \theta ' \cdot \epsilon ^{\mathrm {ram}}[\theta ']}$.
$\pi _{T', \theta ' \cdot \epsilon ^{\mathrm {ram}}[\theta ']}$.
Proof. Under our assumptions, Proposition 8.15 implies that ![]() $\pi _{T', \theta ' \cdot \epsilon ^{\mathrm {ram}}[\theta ']}$ and
$\pi _{T', \theta ' \cdot \epsilon ^{\mathrm {ram}}[\theta ']}$ and ![]() $\pi _{T, \theta \cdot \epsilon ^{\mathrm {ram}}[\theta ]}$ are irreducible and cuspidal (noting that
$\pi _{T, \theta \cdot \epsilon ^{\mathrm {ram}}[\theta ]}$ are irreducible and cuspidal (noting that ![]() $\ell \neq p$ is banal for
$\ell \neq p$ is banal for ![]() $G(F)$ if and only if
$G(F)$ if and only if ![]() $\ell$ is banal for
$\ell$ is banal for ![]() $G(F_{\ell })$, since the residue field cardinalities of
$G(F_{\ell })$, since the residue field cardinalities of ![]() $F_{\ell }$ and of
$F_{\ell }$ and of ![]() $F$ are congruent modulo
$F$ are congruent modulo ![]() $\ell$). The claim then follows from [Reference FengFen24, Theorem 1.2], using Theorem 8.18(ii) to calculate the Tate cohomology of
$\ell$). The claim then follows from [Reference FengFen24, Theorem 1.2], using Theorem 8.18(ii) to calculate the Tate cohomology of ![]() $\pi _{T', \theta ' \cdot \epsilon ^{\mathrm {ram}}[\theta ']}$.
$\pi _{T', \theta ' \cdot \epsilon ^{\mathrm {ram}}[\theta ']}$.
Remark 8.21 One would expect compatibility between the Genestier–Lafforgue correspondence and Kaletha's correspondence for regular supercuspidal representations [Reference KalethaKal19]. No results towards such compatibility are known at present for general groups. In fact, Kaletha's work has not yet been extended to function fields or to mod ![]() $\ell$ representations, but Corollary 8.20 appears to be in accordance with what one would expect from such an extension. Namely, if we instead let
$\ell$ representations, but Corollary 8.20 appears to be in accordance with what one would expect from such an extension. Namely, if we instead let ![]() $F$ be a local field of characteristic zero and residue characteristic
$F$ be a local field of characteristic zero and residue characteristic ![]() $p \neq \ell$ sufficiently large relative to
$p \neq \ell$ sufficiently large relative to ![]() $G$, and let
$G$, and let ![]() $\widetilde {\theta } \colon T(F) \rightarrow \overline {\mathbb {Q}}_{\ell }^{\times }$ be 0-toral, then it is computed in [Reference Chan and OiCO23, § 8] that the
$\widetilde {\theta } \colon T(F) \rightarrow \overline {\mathbb {Q}}_{\ell }^{\times }$ be 0-toral, then it is computed in [Reference Chan and OiCO23, § 8] that the ![]() $L$-parameter of
$L$-parameter of ![]() $\pi _{T, \widetilde {\theta } \cdot \epsilon ^{\mathrm {ram}}[\widetilde {\theta }]}$ (according to Kaletha's correspondence for regular supercuspidal representations) is
$\pi _{T, \widetilde {\theta } \cdot \epsilon ^{\mathrm {ram}}[\widetilde {\theta }]}$ (according to Kaletha's correspondence for regular supercuspidal representations) is
where ![]() $\varphi _{\widetilde {\theta }}$ corresponds to
$\varphi _{\widetilde {\theta }}$ corresponds to ![]() $\widetilde {\theta }$ under local class field theory, and
$\widetilde {\theta }$ under local class field theory, and ![]() ${}^L j$ is determined by
${}^L j$ is determined by ![]() $T \hookrightarrow G$. In particular, this implies that
$T \hookrightarrow G$. In particular, this implies that ![]() $\pi _{T, \widetilde {\theta } \cdot \epsilon ^{\mathrm {ram}}[\widetilde {\theta }]}$ base-changes to
$\pi _{T, \widetilde {\theta } \cdot \epsilon ^{\mathrm {ram}}[\widetilde {\theta }]}$ base-changes to ![]() $\pi _{T', \widetilde {\theta }' \cdot \epsilon ^{\mathrm {ram}}[\widetilde {\theta }']}$ under Kaletha's correspondence for regular supercuspidal representations. One would then expect the same of the mod
$\pi _{T', \widetilde {\theta }' \cdot \epsilon ^{\mathrm {ram}}[\widetilde {\theta }']}$ under Kaletha's correspondence for regular supercuspidal representations. One would then expect the same of the mod ![]() $\ell$ reductions and local function fields
$\ell$ reductions and local function fields ![]() $F$, which suggests the statement of Corollary 8.20.
$F$, which suggests the statement of Corollary 8.20.
Acknowledgements
We thank Anna Cadoret, Charlotte Chan, Hélène Esnault, Kazuhiro Ito, David Hansen, Mikko Korhonen, Marie-France Vignéras, and Weizhe Zheng for helpful conversations.
Conflicts of interest
None.
Financial support
G.B. was supported by the DFG grant CRC/TRR 326, project number 444845124. T.F. was partially supported by an NSF postdoctoral fellowship under grant no. 1902927, as well as the Friends of the Institute for Advanced Study. M.H. was partially supported by NSF grant DMS-2001369 and by a Simons Foundation fellowship, award number 663678. C.K. was partially supported by NSF grant DMS-2200390. J.T.'s work received funding from the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation programme (grant agreement no. 714405).
Journal information
Compositio Mathematica is owned by the Foundation Compositio Mathematica and published by the London Mathematical Society in partnership with Cambridge University Press. All surplus income from the publication of Compositio Mathematica is returned to mathematics and higher education through the charitable activities of the Foundation, the London Mathematical Society and Cambridge University Press.