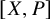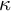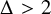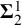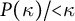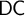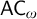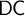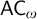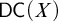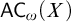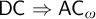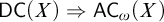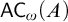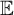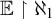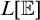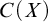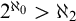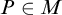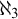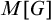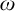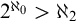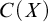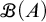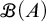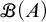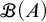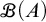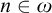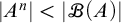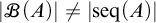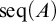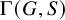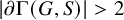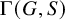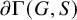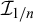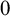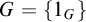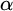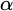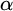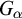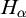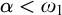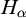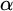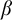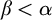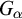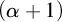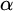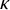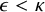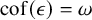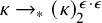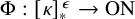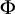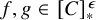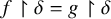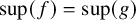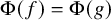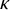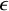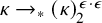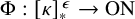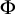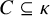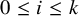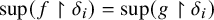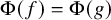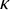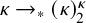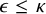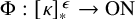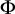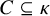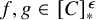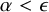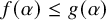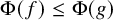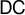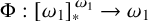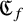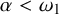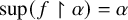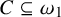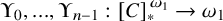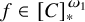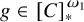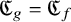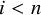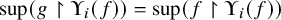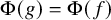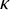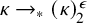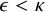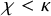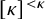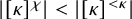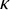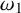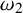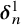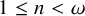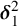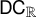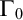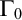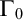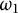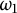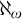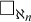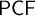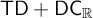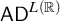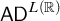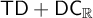284 results in 03EXX
The definable content of homological invariants II: Čech cohomology and homotopy classification
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 12 / 2024
- Published online by Cambridge University Press:
- 06 September 2024, e12
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The Galvin property under the ultrapower axiom
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 27 May 2024, pp. 1-32
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON HOMOMORPHISM GRAPHS
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 12 / 2024
- Published online by Cambridge University Press:
- 13 May 2024, e10
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
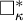
Distributivity and base trees for
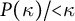 $P(\kappa)/ {\lt} \kappa$
$P(\kappa)/ {\lt} \kappa$
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 07 May 2024, pp. 1-12
-
- Article
- Export citation
DOES
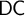 $\mathsf {DC}$ IMPLY
$\mathsf {DC}$ IMPLY 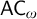 ${\mathsf {AC}}_\omega $, UNIFORMLY?
${\mathsf {AC}}_\omega $, UNIFORMLY?
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 06 May 2024, pp. 1-25
-
- Article
- Export citation
THE DEFINABILITY OF THE EXTENDER SEQUENCE
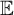 $\mathbb {E}$ FROM
$\mathbb {E}$ FROM 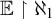 $\mathbb {E}\upharpoonright \aleph _1$ IN
$\mathbb {E}\upharpoonright \aleph _1$ IN 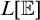 $L[\mathbb {E}]$
$L[\mathbb {E}]$
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 89 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 15 April 2024, pp. 427-459
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
DISCONTINUOUS HOMOMORPHISMS OF
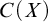 $C(X)$ WITH
$C(X)$ WITH 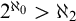 $2^{\aleph _0}>\aleph _2$
$2^{\aleph _0}>\aleph _2$
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 89 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 15 April 2024, pp. 665-696
- Print publication:
- June 2024
-
- Article
- Export citation
CANTOR’S THEOREM MAY FAIL FOR FINITARY PARTITIONS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 03 April 2024, pp. 1-18
-
- Article
- Export citation
WAND/SET THEORIES: A REALIZATION OF CONWAY’S MATHEMATICIANS’ LIBERATION MOVEMENT, WITH AN APPLICATION TO CHURCH’S SET THEORY WITH A UNIVERSAL SET
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 25 March 2024, pp. 1-40
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Structural, point-free, non-Hausdorff topological realization of Borel groupoid actions
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 14 March 2024, e35
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
TWO-CARDINAL DERIVED TOPOLOGIES, INDESCRIBABILITY AND RAMSEYNESS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 12 March 2024, pp. 1-29
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Hyperfiniteness of boundary actions of acylindrically hyperbolic groups
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 11 March 2024, e32
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A UNIFIED APPROACH TO HINDMAN, RAMSEY, AND VAN DER WAERDEN SPACES
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 12 February 2024, pp. 1-53
-
- Article
- Export citation
A HIERARCHY ON NON-ARCHIMEDEAN POLISH GROUPS ADMITTING A COMPATIBLE COMPLETE LEFT-INVARIANT METRIC
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 06 February 2024, pp. 1-19
-
- Article
- Export citation
Almost Everywhere Behavior of Functions According to Partition Measures
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 29 January 2024, e16
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
POINCARÉ–WEYL’S PREDICATIVITY: GOING BEYOND
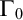 $\Gamma _{0}$
$\Gamma _{0}$
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 30 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 19 January 2024, pp. 41-91
- Print publication:
- March 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
POLISH SPACE PARTITION PRINCIPLES AND THE HALPERN–LÄUCHLI THEOREM
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 19 January 2024, pp. 1-19
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Borel reducibility of equivalence relations on
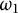 $\omega _1$
$\omega _1$
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 17 January 2024, pp. 1-14
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON COMPACTNESS OF WEAK SQUARE AT SINGULARS OF UNCOUNTABLE COFINALITY
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 04 January 2024, pp. 1-11
-
- Article
- Export citation
NOTE ON
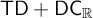 $\mathsf {TD} + \mathsf {DC}_{\mathbb {R}}$ IMPLYING
$\mathsf {TD} + \mathsf {DC}_{\mathbb {R}}$ IMPLYING 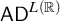 $\mathsf {AD}^{L(\mathbb {R})}$
$\mathsf {AD}^{L(\mathbb {R})}$
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 89 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 04 January 2024, pp. 211-217
- Print publication:
- March 2024
-
- Article
- Export citation

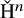 on the category of locally compact separable metric spaces each factor into (i) what we term their
on the category of locally compact separable metric spaces each factor into (i) what we term their 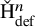 taking values in the category
taking values in the category 

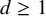
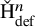 to show that a seminal problem in the development of algebraic topology – namely, Borsuk and Eilenberg’s 1936 problem of classifying, up to homotopy, the maps from a solenoid complement
to show that a seminal problem in the development of algebraic topology – namely, Borsuk and Eilenberg’s 1936 problem of classifying, up to homotopy, the maps from a solenoid complement 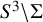
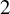
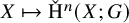 admit two main formulations: a more combinatorial one and a more homotopical formulation as the group
admit two main formulations: a more combinatorial one and a more homotopical formulation as the group 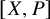
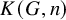
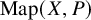
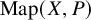
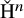 , embodies a substantial variety of classification problems arising throughout mathematics. We show, in particular, that if
, embodies a substantial variety of classification problems arising throughout mathematics. We show, in particular, that if