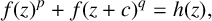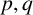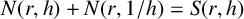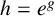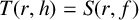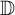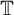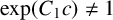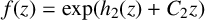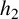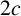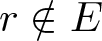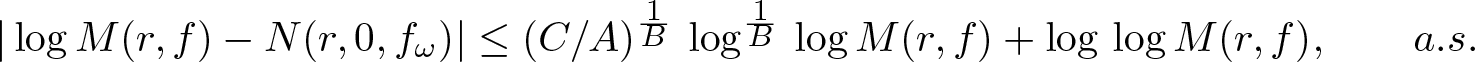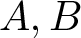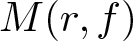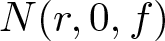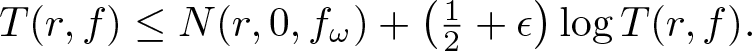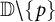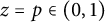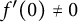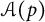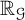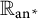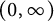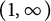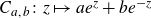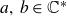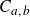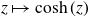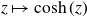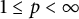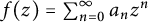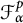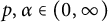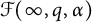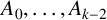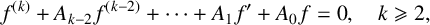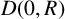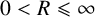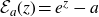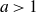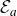135 results in 30Dxx
NOTES ON FERMAT-TYPE DIFFERENCE EQUATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 03 June 2024, pp. 1-12
-
- Article
-
- You have access
- HTML
- Export citation
A classification of automorphic Lie algebras on complex tori
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society , First View
- Published online by Cambridge University Press:
- 28 May 2024, pp. 1-43
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A TROPICAL ANALOGUE OF THE LEMMA ON THE LOGARITHMIC DERIVATIVE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 20 May 2024, pp. 1-10
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Phase retrieval on circles and lines
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 10 May 2024, pp. 1-9
-
- Article
-
- You have access
- HTML
- Export citation
Asymptotic expansions relating to the distribution of the length of longest increasing subsequences
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 15 March 2024, e36
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON THE ITERATIONS AND THE ARGUMENT DISTRIBUTION OF MEROMORPHIC FUNCTIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 116 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 15 February 2024, pp. 145-170
- Print publication:
- April 2024
-
- Article
-
- You have access
- HTML
- Export citation
THE DIFFERENCE ANALOGUE OF THE TUMURA–HAYMAN–CLUNIE THEOREM
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 06 November 2023, pp. 1-10
-
- Article
-
- You have access
- HTML
- Export citation
Normal families and quasiregular mappings
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 23 October 2023, pp. 79-112
-
- Article
-
- You have access
- HTML
- Export citation
Inequalities concerning maximum modulus and zeros of random entire functions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 19 October 2023, pp. 57-78
-
- Article
-
- You have access
- HTML
- Export citation
Sparse analytic systems
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 04 July 2023, e58
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Improved Bloch and Landau constants for meromorphic functions
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 28 April 2023, pp. 1269-1273
- Print publication:
- December 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Multiply connected wandering domains of meromorphic functions: the pursuit of uniform internal dynamics
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 3 / March 2024
- Published online by Cambridge University Press:
- 11 April 2023, pp. 727-748
- Print publication:
- March 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
BOUNDS FOR FUNCTIONALS DEFINED ON A CERTAIN CLASS OF MEROMORPHIC FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 03 March 2023, pp. 101-109
- Print publication:
- February 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Multisummability for generalized power series
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 27 February 2023, pp. 458-494
- Print publication:
- April 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Iterates of meromorphic functions on escaping Fatou components
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 6 / December 2023
- Published online by Cambridge University Press:
- 22 November 2022, pp. 1906-1928
- Print publication:
- December 2023
-
- Article
- Export citation
Topological dynamics of cosine maps
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 174 / Issue 3 / May 2023
- Published online by Cambridge University Press:
- 23 September 2022, pp. 497-529
- Print publication:
- May 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Zero and uniqueness sets for Fock spaces
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 25 July 2022, pp. 532-543
- Print publication:
- June 2023
-
- Article
- Export citation
Two problems on random analytic functions in Fock spaces
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 4 / August 2023
- Published online by Cambridge University Press:
- 08 July 2022, pp. 1176-1198
- Print publication:
- August 2023
-
- Article
- Export citation
DESCRIPTION OF GROWTH AND OSCILLATION OF SOLUTIONS OF COMPLEX LDE’S
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 115 / Issue 2 / October 2023
- Published online by Cambridge University Press:
- 16 June 2022, pp. 145-171
- Print publication:
- October 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Dynamics of generalised exponential maps
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 174 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 21 April 2022, pp. 123-136
- Print publication:
- January 2023
-
- Article
- Export citation