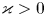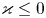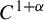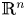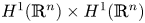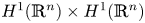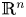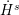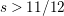27 results in 37Lxx
EMBED IN ENSEMBLE TO RIGOROUSLY AND ACCURATELY HOMOGENIZE QUASI-PERIODIC MULTI-SCALE HETEROGENEOUS MATERIAL
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 66 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 19 September 2024, pp. 1-34
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Slow passage through the Busse balloon – predicting steps on the Eckhaus staircase
- Part of
-
- Journal:
- European Journal of Applied Mathematics , First View
- Published online by Cambridge University Press:
- 16 April 2024, pp. 1-26
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Invariant measures and large deviation principles for stochastic Schrödinger delay lattice systems
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 04 March 2024, pp. 1-42
-
- Article
-
- You have access
- HTML
- Export citation
On degenerate reaction-diffusion epidemic models with mass action or standard incidence mechanism
- Part of
-
- Journal:
- European Journal of Applied Mathematics , First View
- Published online by Cambridge University Press:
- 22 January 2024, pp. 1-28
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the linearized Whitham–Broer–Kaup system on bounded domains
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 07 September 2023, pp. 1-20
-
- Article
-
- You have access
- HTML
- Export citation
Estimates for evolutionary partial differential equations in classical function spaces
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 01 September 2023, e76
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Synchronization of coupled map lattices
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 30 March 2023, pp. 143-163
-
- Article
-
- You have access
- HTML
- Export citation
Measures of maximal and full dimension for smooth maps
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 17 March 2023, pp. 31-49
- Print publication:
- January 2024
-
- Article
-
- You have access
- HTML
- Export citation
Zero entropy and stable rotation sets for monotone recurrence relations
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 5 / May 2023
- Published online by Cambridge University Press:
- 05 April 2022, pp. 1737-1759
- Print publication:
- May 2023
-
- Article
- Export citation
Periodic trajectories for an age-structured prey–predator system with Michaelis–Menten functional response including delays and asymmetric diffusion
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 33 / Issue 4 / August 2022
- Published online by Cambridge University Press:
- 12 May 2021, pp. 587-605
-
- Article
- Export citation
Existence of solution for elliptic equations with supercritical Trudinger–Moser growth
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 16 February 2021, pp. 291-310
- Print publication:
- April 2022
-
- Article
- Export citation
Asymptotically autonomous robustness of random attractors for a class of weakly dissipative stochastic wave equations on unbounded domains
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 6 / December 2021
- Published online by Cambridge University Press:
- 05 November 2020, pp. 1700-1730
- Print publication:
- December 2021
-
- Article
- Export citation
Transition waves for lattice Fisher-KPP equations with time and space dependence
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 28 April 2020, pp. 573-600
- Print publication:
- April 2021
-
- Article
- Export citation
LYAPUNOV EXPONENTS OF THE KURAMOTO–SIVASHINSKY PDE
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 61 / Issue 3 / July 2019
- Published online by Cambridge University Press:
- 15 July 2019, pp. 270-285
-
- Article
-
- You have access
- Export citation
GLOBAL ATTRACTOR FOR WEAKLY DAMPED, FORCED mKdV EQUATION BELOW ENERGY SPACE
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 241 / March 2021
- Published online by Cambridge University Press:
- 20 June 2019, pp. 171-203
- Print publication:
- March 2021
-
- Article
- Export citation
On non-autonomously forced Burgers equation with periodic and Dirichlet boundary conditions
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 4 / August 2020
- Published online by Cambridge University Press:
- 14 March 2019, pp. 2025-2054
- Print publication:
- August 2020
-
- Article
- Export citation
Long-time asymptotic expansions for Navier-Stokes equations with power-decaying forces
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 22 January 2019, pp. 569-606
- Print publication:
- April 2020
-
- Article
- Export citation
Kolmogorov's dissipation number and the number of degrees of freedom for the 3D Navier–Stokes equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 2 / April 2019
- Published online by Cambridge University Press:
- 15 January 2019, pp. 429-446
- Print publication:
- April 2019
-
- Article
- Export citation
SPATIAL HAMILTONIAN IDENTITIES FOR NONLOCALLY COUPLED SYSTEMS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 6 / 2018
- Published online by Cambridge University Press:
- 14 November 2018, e22
-
- Article
-
- You have access
- Open access
- Export citation
Time-dependent attractors for non-autonomous non-local reaction–diffusion equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 148 / Issue 5 / October 2018
- Published online by Cambridge University Press:
- 22 April 2018, pp. 957-981
- Print publication:
- October 2018
-
- Article
- Export citation