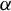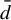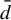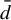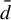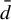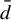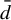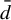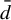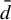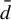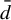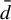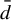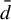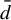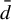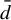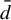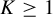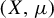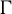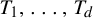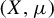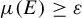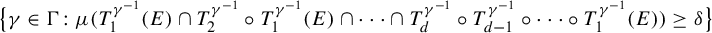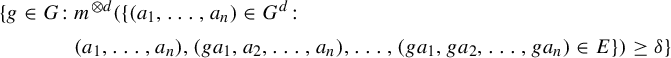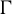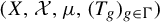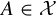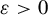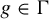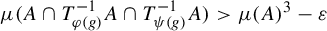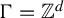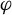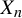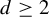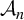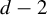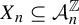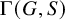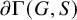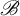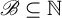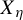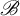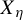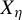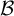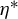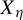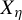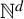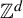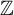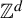325 results in 37Axx
A recurrence-type strong Borel–Cantelli lemma for Axiom A diffeomorphisms
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 18 September 2024, pp. 1-20
-
- Article
- Export citation
On transversal Hölder regularity for flat Wieler solenoids
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 10 September 2024, pp. 1-27
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Minimal and proximal examples of
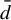 $\bar {d}$-stable and
$\bar {d}$-stable and 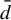 $\bar {d}$-approachable shift spaces
$\bar {d}$-approachable shift spaces
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 10 September 2024, pp. 1-31
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Uniform syndeticity in multiple recurrence
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 28 May 2024, pp. 1-22
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A variational principle of amenable random metric mean dimensions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society , First View
- Published online by Cambridge University Press:
- 16 May 2024, pp. 1-24
-
- Article
- Export citation
Co-spectral radius for countable equivalence relations
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 10 May 2024, pp. 1-43
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Weighted topological pressure revisited
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 08 May 2024, pp. 1-37
-
- Article
- Export citation
Poissonian pair correlation for directions in multi-dimensional affine lattices and escape of mass estimates for embedded horospheres
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 26 April 2024, pp. 1-29
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Khintchine-type double recurrence in abelian groups
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 24 April 2024, pp. 1-33
-
- Article
- Export citation
Schmidt games and Cantor winning sets
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 19 April 2024, pp. 1-40
-
- Article
- Export citation
Non-existence of a universal zero-entropy system via generic actions of almost complete growth
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 12 April 2024, pp. 1-15
-
- Article
- Export citation
Entropy, virtual Abelianness and Shannon orbit equivalence
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 02 April 2024, pp. 1-20
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Rigidity of pressures of Hölder potentials and the fitting of analytic functions through them
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 18 March 2024, pp. 1-35
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Approximate homomorphisms and sofic approximations of orbit equivalence relations
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 15 March 2024, pp. 1-26
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THERMODYNAMIC FORMALISM FOR AMENABLE GROUPS AND COUNTABLE STATE SPACES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu , First View
- Published online by Cambridge University Press:
- 15 March 2024, pp. 1-65
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Discrepancy of rational points in simple algebraic groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 4 / April 2024
- Published online by Cambridge University Press:
- 13 March 2024, pp. 836-877
- Print publication:
- April 2024
-
- Article
- Export citation
Measure transfer and S-adic developments for subshifts
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 11 March 2024, pp. 1-35
-
- Article
- Export citation
Hyperfiniteness of boundary actions of acylindrically hyperbolic groups
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 11 March 2024, e32
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Invariant measures for
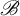 $\mathscr {B}$-free systems revisited
$\mathscr {B}$-free systems revisited
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 08 March 2024, pp. 1-32
-
- Article
- Export citation
Bohr chaoticity of principal algebraic actions and Riesz product measures
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 06 March 2024, pp. 1-27
-
- Article
-
- You have access
- Open access
- HTML
- Export citation