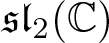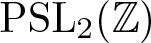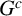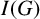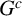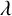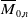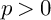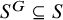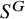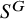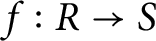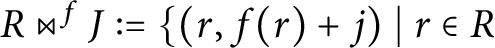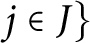118 results in 13Axx
Derived functors and Hilbert Polynomials over regular local rings
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society , First View
- Published online by Cambridge University Press:
- 23 October 2024, pp. 1-11
-
- Article
-
- You have access
- HTML
- Export citation
The Hilbert series of the superspace coinvariant ring
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 12 / 2024
- Published online by Cambridge University Press:
- 17 October 2024, e16
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A classification of automorphic Lie algebras on complex tori
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 3 / August 2024
- Published online by Cambridge University Press:
- 28 May 2024, pp. 947-989
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON THE SET OF BETTI ELEMENTS OF A PUISEUX MONOID
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 20 May 2024, pp. 1-13
-
- Article
-
- You have access
- HTML
- Export citation
Ideals with componentwise linear powers
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 12 March 2024, pp. 833-841
- Print publication:
- September 2024
-
- Article
-
- You have access
- HTML
- Export citation
Lattice points in slices of prisms
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 08 March 2024, pp. 1-28
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
COUNTING GEOMETRIC BRANCHES VIA THE FROBENIUS MAP AND F-NILPOTENT SINGULARITIES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 255 / September 2024
- Published online by Cambridge University Press:
- 27 February 2024, pp. 724-741
- Print publication:
- September 2024
-
- Article
-
- You have access
- HTML
- Export citation
HOMOLOGICAL LINEAR QUOTIENTS AND EDGE IDEALS OF GRAPHS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 2 / October 2024
- Published online by Cambridge University Press:
- 29 January 2024, pp. 291-302
- Print publication:
- October 2024
-
- Article
-
- You have access
- HTML
- Export citation
Lim Ulrich sequences and Boij-Söderberg cones
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 18 December 2023, e115
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
HOW TO EXTEND CLOSURE AND INTERIOR OPERATIONS TO MORE MODULES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 255 / September 2024
- Published online by Cambridge University Press:
- 01 December 2023, pp. 513-560
- Print publication:
- September 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Tropical invariants for binary quintics and reduction types of Picard curves
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 66 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 06 November 2023, pp. 65-87
- Print publication:
- January 2024
-
- Article
-
- You have access
- HTML
- Export citation
CODIMENSION ONE FOLIATIONS IN POSITIVE CHARACTERISTIC
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 4 / July 2024
- Published online by Cambridge University Press:
- 06 November 2023, pp. 1705-1750
- Print publication:
- July 2024
-
- Article
-
- You have access
- HTML
- Export citation
A VARIANT OF PERFECTOID ABHYANKAR’S LEMMA AND ALMOST COHEN–MACAULAY ALGEBRAS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 253 / March 2024
- Published online by Cambridge University Press:
- 04 September 2023, pp. 164-215
- Print publication:
- March 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
When are the natural embeddings of classical invariant rings pure?
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 03 August 2023, e67
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A characterisation of atomicity
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 175 / Issue 2 / September 2023
- Published online by Cambridge University Press:
- 24 April 2023, pp. 459-465
- Print publication:
- September 2023
-
- Article
-
- You have access
- HTML
- Export citation
On parabolic subgroups of symplectic reflection groups
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue 2 / May 2023
- Published online by Cambridge University Press:
- 10 January 2023, pp. 401-413
- Print publication:
- May 2023
-
- Article
-
- You have access
- HTML
- Export citation
Lower bounds on Hilbert–Kunz multiplicities and maximal F-signatures
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 174 / Issue 2 / March 2023
- Published online by Cambridge University Press:
- 21 December 2022, pp. 247-271
- Print publication:
- March 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ANALYTIC SPREAD OF FILTRATIONS ON TWO-DIMENSIONAL NORMAL LOCAL RINGS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 249 / March 2023
- Published online by Cambridge University Press:
- 23 November 2022, pp. 239-268
- Print publication:
- March 2023
-
- Article
-
- You have access
- HTML
- Export citation
Maximum likelihood estimation for tensor normal models via castling transforms
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 01 July 2022, e50
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Hilbert rings with maximal ideals of different heights and unruly Hilbert rings
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 10 March 2022, pp. 196-203
- Print publication:
- March 2023
-
- Article
-
- You have access
- HTML
- Export citation