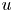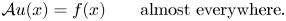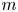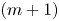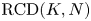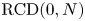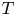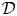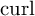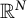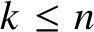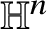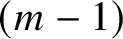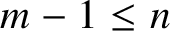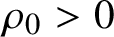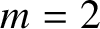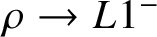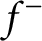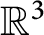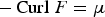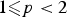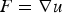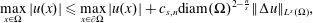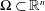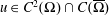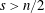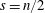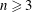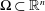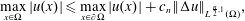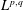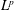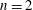42 results in 49Qxx
Rigidity for the perimeter inequality under Schwarz symmetrization
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 03 June 2024, pp. 1-27
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the support of measures with fixed marginals with applications in optimal mass transportation
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 29 May 2024, pp. 1-10
-
- Article
-
- You have access
- HTML
- Export citation
A remark on a conjecture on the symmetric Gaussian problem
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 2 / May 2024
- Published online by Cambridge University Press:
- 15 April 2024, pp. 643-661
-
- Article
-
- You have access
- HTML
- Export citation
A boundary maximum principle for stationary pairs of varifolds with fixed contact angle
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 2 / May 2024
- Published online by Cambridge University Press:
- 08 March 2024, pp. 316-335
-
- Article
-
- You have access
- HTML
- Export citation
On the lack of compactness in the axisymmetric neo-Hookean model
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 26 February 2024, e26
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A Lebesgue–Lusin property for linear operators of first and second order
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 06 November 2023, pp. 1-11
-
- Article
-
- You have access
- HTML
- Export citation
Topological regularity of isoperimetric sets in PI spaces having a deformation property
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 09 October 2023, pp. 1-23
-
- Article
-
- You have access
- HTML
- Export citation
Non-local approximation of free-discontinuity problems in linear elasticity and application to stochastic homogenisation
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 4 / August 2024
- Published online by Cambridge University Press:
- 08 June 2023, pp. 1060-1094
- Print publication:
- August 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Involutivity of distributions at points of superdense tangency with respect to normal currents
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 24 March 2023, pp. 508-524
- Print publication:
- April 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
COMPACTNESS AND STRUCTURE OF ZERO-STATES FOR UNORIENTED AVILES–GIGA FUNCTIONALS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 2 / March 2024
- Published online by Cambridge University Press:
- 10 March 2023, pp. 941-982
- Print publication:
- March 2024
-
- Article
-
- You have access
- HTML
- Export citation
Optimization of the anisotropic Cheeger constant with respect to the anisotropy
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 17 February 2023, pp. 1030-1043
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Relaxation for an optimal design problem in BD(Ω)
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 10 March 2022, pp. 721-763
- Print publication:
- June 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Lipschitz graphs and currents in Heisenberg groups
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 02 February 2022, e6
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Three candidate plurality is stablest for small correlations
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 28 September 2021, e65
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Nontame Morse–Smale flows and odd Chern–Weil theory
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 74 / Issue 6 / December 2022
- Published online by Cambridge University Press:
- 06 July 2021, pp. 1579-1624
- Print publication:
- December 2022
-
- Article
- Export citation
Tight frames and related geometric problems
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 18 December 2020, pp. 942-963
- Print publication:
- December 2021
-
- Article
- Export citation
Optimal free export/import regions
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 17 September 2020, pp. 737-751
- Print publication:
- December 2021
-
- Article
- Export citation
Reflection of Willmore Surfaces with Free Boundaries
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 3 / June 2021
- Published online by Cambridge University Press:
- 11 March 2020, pp. 787-804
- Print publication:
- June 2021
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Analytic and geometric properties of dislocation singularities
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 4 / August 2020
- Published online by Cambridge University Press:
- 01 February 2019, pp. 1609-1651
- Print publication:
- August 2020
-
- Article
- Export citation
An Endpoint Alexandrov Bakelman Pucci Estimate in the Plane
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 3 / September 2019
- Published online by Cambridge University Press:
- 11 January 2019, pp. 643-651
- Print publication:
- September 2019
-
- Article
-
- You have access
- Export citation