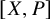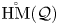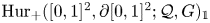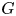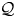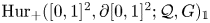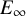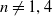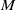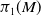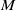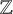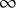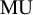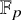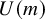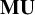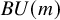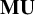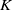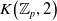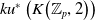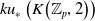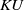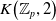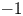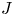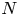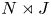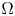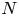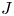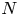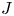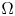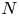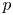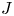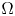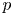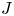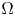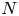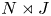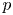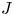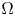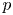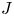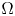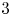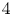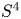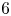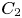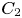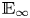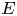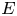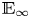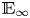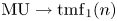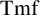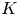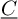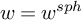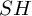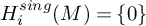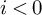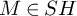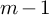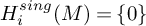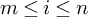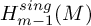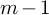79 results in 55Nxx
The definable content of homological invariants II: Čech cohomology and homotopy classification
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 12 / 2024
- Published online by Cambridge University Press:
- 06 September 2024, e12
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Deloopings of Hurwitz spaces
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 7 / July 2024
- Published online by Cambridge University Press:
- 13 September 2024, pp. 1651-1714
- Print publication:
- July 2024
-
- Article
- Export citation
TWISTED ACTIONS ON COHOMOLOGIES AND BIMODULES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 31 May 2024, pp. 1-52
-
- Article
- Export citation
Adams’ cobar construction as a monoidal
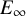 $E_{\infty }$-coalgebra model of the based loop space
$E_{\infty }$-coalgebra model of the based loop space
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 15 May 2024, e62
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Simplicial volume of manifolds with amenable fundamental group at infinity
- Part of
-
- Journal:
- Glasgow Mathematical Journal , First View
- Published online by Cambridge University Press:
- 22 April 2024, pp. 1-8
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Dirac geometry II: coherent cohomology
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 27 February 2024, e27
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Chern classes in equivariant bordism
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 05 January 2024, e7
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The connective
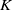 $K$-theory of the Eilenberg–MacLane space
$K$-theory of the Eilenberg–MacLane space 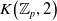 $K\!\left({\mathbb{Z}}_p,\textrm{2}\right)$
$K\!\left({\mathbb{Z}}_p,\textrm{2}\right)$
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 66 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 11 December 2023, pp. 188-220
- Print publication:
- January 2024
-
- Article
- Export citation
On equivariant topological modular forms
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 12 / December 2023
- Published online by Cambridge University Press:
- 06 November 2023, pp. 2638-2693
- Print publication:
- December 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
From the Mayer–Vietoris spectral sequence to überhomology
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 02 October 2023, pp. 1-24
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Fixed point conditions for non-coprime actions
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 11 September 2023, pp. 1-7
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Realization of GKM fibrations and new examples of Hamiltonian non-Kähler actions
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 10 / October 2023
- Published online by Cambridge University Press:
- 24 August 2023, pp. 2149-2190
- Print publication:
- October 2023
-
- Article
- Export citation
Reflexive homology
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 03 August 2023, pp. 1-28
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Obstruction theory and the level n elliptic genus
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 9 / September 2023
- Published online by Cambridge University Press:
- 03 August 2023, pp. 2000-2021
- Print publication:
- September 2023
-
- Article
- Export citation
MORAVA K-THEORY AND FILTRATIONS BY POWERS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu , First View
- Published online by Cambridge University Press:
- 04 July 2023, pp. 1-77
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Girth, magnitude homology and phase transition of diagonality
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 09 February 2023, pp. 221-247
- Print publication:
- February 2024
-
- Article
- Export citation
Equivariant Brill–Noether theory for elliptic operators and superrigidity of J-holomorphic maps
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 16 January 2023, e3
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ELLIPTIC COHOMOLOGY IS UNIQUE UP TO HOMOTOPY
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 115 / Issue 1 / August 2023
- Published online by Cambridge University Press:
- 15 November 2022, pp. 99-118
- Print publication:
- August 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Enough vector bundles on orbispaces
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 11 / November 2022
- Published online by Cambridge University Press:
- 28 November 2022, pp. 2046-2081
- Print publication:
- November 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON MORPHISMS KILLING WEIGHTS AND STABLE HUREWICZ-TYPE THEOREMS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 2 / March 2024
- Published online by Cambridge University Press:
- 24 October 2022, pp. 521-556
- Print publication:
- March 2024
-
- Article
- Export citation

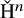 on the category of locally compact separable metric spaces each factor into (i) what we term their
on the category of locally compact separable metric spaces each factor into (i) what we term their 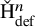 taking values in the category
taking values in the category 

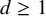
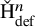 to show that a seminal problem in the development of algebraic topology – namely, Borsuk and Eilenberg’s 1936 problem of classifying, up to homotopy, the maps from a solenoid complement
to show that a seminal problem in the development of algebraic topology – namely, Borsuk and Eilenberg’s 1936 problem of classifying, up to homotopy, the maps from a solenoid complement 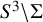
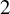
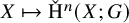 admit two main formulations: a more combinatorial one and a more homotopical formulation as the group
admit two main formulations: a more combinatorial one and a more homotopical formulation as the group 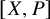
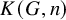
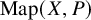
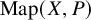
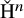 , embodies a substantial variety of classification problems arising throughout mathematics. We show, in particular, that if
, embodies a substantial variety of classification problems arising throughout mathematics. We show, in particular, that if