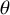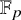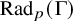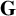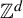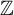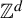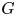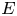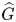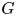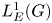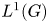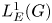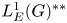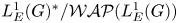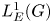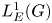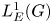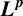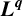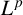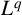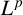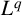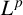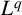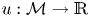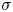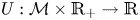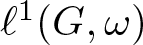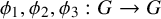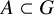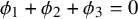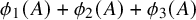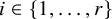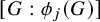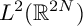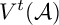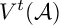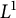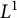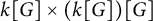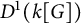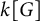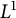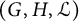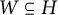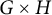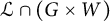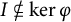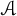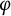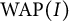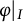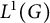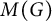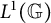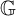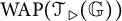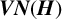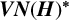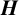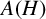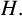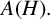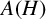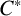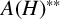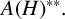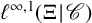246 results in 43Axx
Bounds on multiplicities of symmetric pairs of finite groups
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 09 September 2024, e73
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Weak amenability for dual Banach algebras
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society , First View
- Published online by Cambridge University Press:
- 29 April 2024, pp. 1-9
-
- Article
- Export citation
Thompson’s semigroup and the first Hochschild cohomology
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 07 March 2024, pp. 1-21
-
- Article
- Export citation
Bohr chaoticity of principal algebraic actions and Riesz product measures
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 06 March 2024, pp. 1-27
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Arens regularity of ideals of the group algebra of a compact Abelian group
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 27 October 2023, pp. 1-17
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
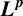 $\boldsymbol {L}^{\boldsymbol {p}}$–
$\boldsymbol {L}^{\boldsymbol {p}}$–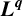 $\boldsymbol {L}^{\boldsymbol {q}}$ MULTIPLIERS ON COMMUTATIVE HYPERGROUPS
$\boldsymbol {L}^{\boldsymbol {q}}$ MULTIPLIERS ON COMMUTATIVE HYPERGROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 115 / Issue 3 / December 2023
- Published online by Cambridge University Press:
- 18 October 2023, pp. 375-395
- Print publication:
- December 2023
-
- Article
- Export citation
A COUNTEREXAMPLE TO A RESULT OF JABERI AND MAHMOODI
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 10 August 2023, pp. 1-3
-
- Article
- Export citation
WIENER TAUBERIAN THEOREMS FOR CERTAIN BANACH ALGEBRAS ON REAL RANK ONE SEMISIMPLE LIE GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 116 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 18 July 2023, pp. 68-95
- Print publication:
- February 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A revisit to “On BMO and Carleson measures on Riemannian manifolds”
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 18 July 2023, pp. 1-27
-
- Article
- Export citation
On the Dales–Żelazko conjecture for Beurling algebras on discrete groups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 3 / August 2023
- Published online by Cambridge University Press:
- 03 July 2023, pp. 613-624
-
- Article
- Export citation
Bohr sets in sumsets II: countable abelian groups
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 03 July 2023, e57
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
TWISTED SHIFT-INVARIANT SYSTEM IN
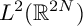 $L^2(\mathbb {R}^{2N})$
$L^2(\mathbb {R}^{2N})$
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 251 / September 2023
- Published online by Cambridge University Press:
- 05 June 2023, pp. 734-767
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Stable finiteness of twisted group rings and noisy linear cellular automata
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 22 May 2023, pp. 1-20
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Linear preservers on idempotents of Fourier algebras
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 17 May 2023, pp. 1326-1340
- Print publication:
- December 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Abstract almost periodicity for group actions on uniform topological spaces
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 11 April 2023, pp. 798-829
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Fourier transformable measures with weak Meyer set support and their lift to the cut-and-project scheme
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 17 February 2023, pp. 1044-1060
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON THE DOUBLING CONDITION IN THE INFINITE-DIMENSIONAL SETTING
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 3 / December 2023
- Published online by Cambridge University Press:
- 09 February 2023, pp. 480-491
- Print publication:
- December 2023
-
- Article
- Export citation
Invariant means on weakly almost periodic functionals with application to quantum groups
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 16 January 2023, pp. 927-936
- Print publication:
- September 2023
-
- Article
- Export citation
ON THE ALGEBRAS
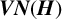 $\boldsymbol {VN(H)}$ AND
$\boldsymbol {VN(H)}$ AND 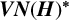 $\boldsymbol {VN(H)^{*}} $ OF AN ULTRASPHERICAL HYPERGROUP
$\boldsymbol {VN(H)^{*}} $ OF AN ULTRASPHERICAL HYPERGROUP 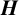 $\boldsymbol {H}$
$\boldsymbol {H}$
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 115 / Issue 3 / December 2023
- Published online by Cambridge University Press:
- 12 December 2022, pp. 337-353
- Print publication:
- December 2023
-
- Article
- Export citation
A CRITERION FOR HYPERSYMMETRY ON DISCRETE GROUPOIDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 2 / October 2023
- Published online by Cambridge University Press:
- 05 December 2022, pp. 320-330
- Print publication:
- October 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation